INTRODUCCIÓN
En el proceso de resolución de un problema matemático el hombre se apoya en principios, reglas y estrategias heurísticas. Si la solución del problema requiere de conocimientos geométricos, entonces es importante, en múltiples ocasiones, construir una figura geométrica con las condiciones dadas en el problema. Por ello las construcciones geométricas resultan de especial importancia en el contenido de la matemática y aparece desde las primeras edades en los diferentes currículos del mundo.
Álvarez, Almeida y Villegas evidencian que: “En todos los niveles de educación los alumnos deben aprender a resolver problemas matemáticos en sentido amplio, en tanto se sitúan ante situaciones problemáticas que exigen que movilicen sus recursos personológicos hacia el logro de un objetivo, para el cual no poseen de antemano una vía de solución conocida” (Álvarez, Almeida y Villegas, 2014). Y proponen a los profesores que: “Debe enseñarse a los niños desde los primeros grados a utilizar estrategias diversas en la resolución de problemas, entiéndase recursos heurísticos y metacognitivos. La utilización de materiales manipulativos, la realización de dibujos, el esbozo de figuras, la construcción de modelos lineales, tablas de doble entrada o diagramas, la conveniencia de un tanteo inteligente, de aprovechar las utilidades de calculadoras o medios informáticos, de buscar relaciones, establecer analogías, de analizar casos particulares, de medir y comparar, de monitorear lo que se hace por diversas vías, son algunos de los recursos que deben aprender progresivamente” (Álvarez, Almeida y Villegas, 2014).
Varios autores que han abordado la resolución de problemas y el desarrollo del pensamiento geométrico-espacial confirman la afirmación anterior. Carrasco (2004) desde la heúristica para la resolución de problemas propone la aplicación de los principios, reglas y estrategias heurísticas que evidencian la importancia de las construcciones geométricas. Campistrous y Rizo (2007) aplican estos procedimientos heurísticos a la resolución de problemas, vinculados a la tecnología. Crespo en esta última dirección expuso que: “la tendencia internacional es que muchos problemas que se resolvían tradicionalmente a base de álgebra se pueden ahora resolver de forma más efectiva y general usando la representación geométrica y las técnicas de gráfica por ordenador” (Crespo, 2007).
Ron (2007) realiza una sistematización de los principales autores que en Cuba y en el mundo han abordado el tema de resolución de problemas para proponer una estrategia didáctica en este sentido. Otros autores se encuentran en esta sistematización y coinciden en la elaboración de un modelo como parte de la solución de un problema. Las construcciones geométricas, en los problemas geométricos, son parte integrante del modelo que se plantean. Ron define una serie de términos que se asume en esta investigación:
“Se asume por solución de un problema todo objeto que satisfaga la exigencia planteada; por vía de solución, todo conjunto de proposiciones verdaderas que a través de inferencias enlaza el planteamiento inicial (elementos dados, datos) con la exigencia (incógnita, elementos buscados), y por resolución de problemas el proceso mediante el cual se construye la vía de solución o se contradice la existencia de una vía” (Ron, 2007).
Coro en su obra relativa al pensamiento geométrico espacial expone la relación de las construcciones geométricas en los procesos mentales cuando expone que:
“En la matemática, la comprensión y operación de conceptos exige un alto grado de abstracción, de ahí resulta el importante rol que desempeñan procesos como la representación y la visualización. La visualización para muchos investigadores se manifiesta tanto interna como externamente y está estrechamente relacionada con la formación y obtención de imágenes, también la asocian con la construcción y la manipulación de representaciones mentales de objetos de dos y tres dimensiones y la percepción de los objetos desde diferentes perspectivas” (Coro, 2019).
La experiencia de los autores de este artículo relativa a las construcciones geométricas en el proceso de resolución de problemas se concreta en el entrenamiento a los estudiantes de la enseñanza media para los concursos de matemática. Las construcciones geométricas, en los problemas de concurso, resultan muy complejas y definitorias por la complejidad de las vías de solución. El profesor entrenador tiene que proponer ejercicios para que los estudiantes realicen construcciones geométricas y mostrarles a los estudiantes la importancia de realizarlas para llegar a la solución.
Por esto el objetivo de este artículo es demostrar la importancia de las construcciones geométricas en el proceso de resolución de problemas para los estudiantes de concursos. Para lo que proponemos las construcciones geométricas a realizar en tres problemas extraídos de las Olimpiadas Iraníes de Geometría junto a algunas recomendaciones metodológicas a realizar.
DESARROLLO
El primer problema es el número 1 del nivel elemental de IGO (2014), elaborado por Etesami Fard:
En un triángulo rectángulo ABC se tiene que: ∠A = 900 y ∠C = 300. Sea w la circunferencia que pasa por A y es tangente al lado BC en su punto medio. Asuma que w interseca al lado AC y a la circunferencia circunscrita al triángulo ABC en N y M, respectivamente. Prueba que MN ⊥ BC.
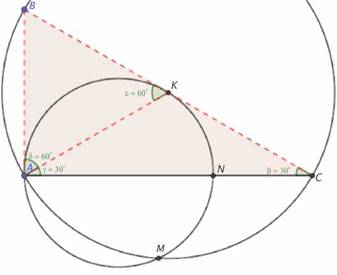
En este tipo de problemas es conveniente realizar varios esbozos de la figura hasta tener algunas ideas acerca de los hechos geométricos que pudieran tener lugar y que pueden sugerir ideas de cómo enfrentar el problema. En primer lugar, se debe reflexionar acerca del orden más adecuado a la hora de realizar la construcción de la figura. Consideramos aconsejable construir primero la circunferencia w, para luego trazar la línea tangente BC, después la circunferencia de centro K y diámetro BC, y finalmente el triángulo rectángulo ABC teniendo en cuenta que A es uno de los puntos de intersección de las dos circunferencias (Fig. 1).
También es muy útil el empleo de la estrategia trabajo hacia atrás, es decir, considerar que ya sabemos que MN ⊥ BC y analizar todas implicaciones que esto trae consigo. De estas reflexiones se pueden derivar conclusiones tales como: el menor de los ángulos formado por las rectas MN y AC tiene que tener una amplitud de 60o, la recta MN tiene que contener a la altura relativa al lado BC en el triángulo KNC o a la altura relativa al mismo lado en el triángulo KMC, si prolongamos MN hasta que interseque nuevamente a la circunferencia circunscrita al triángulo ABC, el diámetro BC tiene que ser mediatriz de la nueva cuerda formada. En la presente solución probaremos la primera de las conclusiones anteriormente citadas.
El dominio de los conceptos relacionados en el problema sugiere la idea de trazar los segmentos:
AK, para obtener los triángulos isósceles KAC y BAK, de donde se obtiene que ∠KAC = ∠C =30o y por ende, ∠BAK = ∠A - ∠KAC = 60o que a su vez permite concluir que el triángulo BAK es equilátero (Fig. 2).
KN, KM y AM, para construir los ángulos inscritos ∠ANK, ∠AMK, ∠AKM y ∠MKN; y los ángulos seminscritos ∠AKB y ∠NKC. De lo anterior se obtienen los siguientes resultados: ∠ANK = ∠AMK = ∠AKB = 60o, lo cual implica que el triángulo AMK es equilátero (AK = KM por ser radios de w) y, por consiguiente, ∠PNC = ∠ANM = ∠AKM =60o siendo P el punto de intersección de las rectas MN y BC. De este último hallazgo se deduce que el triángulo CPN es rectángulo en P y por tanto MN ⊥ BC (Fig. 3).
El segundo problema, propuesto por Vakili, es el problema 2 de IGO (2015):
En un triángulo acutángulo ABC el segmento BH es la altura desde el vértice B. Los puntos D y E son los puntos medios de los lados AB y AC, respectivamente. Suponga que F es la reflexión de H con respecto a la recta ED. Pruebe que la recta BF pasa a través del circuncentro O del triángulo ABC.
Probar que la recta BF pasa por el punto O es equivalente a probar que los puntos B, F y O son colineales. Los problemas que involucran colinealidad de puntos son muy variados al igual que las diferentes vías para enfrentarlos, entre las cuales resulta de vital importancia el trabajo con ángulos. Al respecto vale la pena tener en cuenta tres ideas:
Si A, B y C son puntos alineados y D, B y E son tres puntos no colineales con los anteriores; D, B y E serán colineales si y solo si ∠ABD = ∠CBE.
Sean los puntos A, B, C y D tales que A, B y D; B, C y D no son colineales. Los puntos A, B y C serán colineales si y solo si: ∠ABC = ∠ABD + ∠DBC =180o.
Sean los puntos A, B, C y D no todos colineales; los puntos B, C y D serán colineales si y solo si ∠ABC = ∠ABD.
Un antecedente importante de este problema lo constituye el siguiente resultado: si O es el circuncentro del triángulo ABC, entonces ∠AOB = 2∠C y por ende ∠OBA =90o - ∠C.
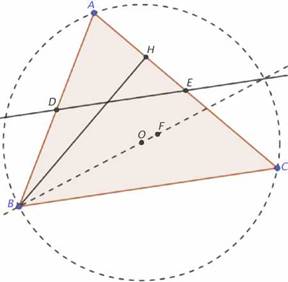
En problemas como este hay que tener en cuenta que la figura que se represente tiene que ser lo más general posible: en el caso que nos ocupa un triángulo escaleno y acutángulo (Fig. 4).
Analicemos dos soluciones:
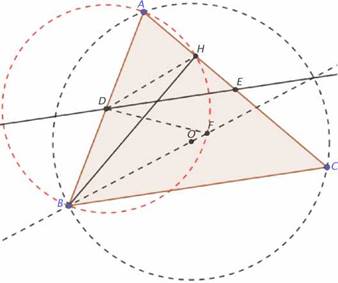
La primera solución consiste en probar que: ∠FBA = 90o - ∠C. El hecho de que el triángulo BHA es rectángulo en H y que D es el punto medio de la hipotenusa, unido a las propiedades de la reflexión permiten concluir que: AD = DH = DF = DB lo cual conduce a que A, H, F y B pertenecen a la circunferencia con centro en D y diámetro AB, lo cual sugiere construir esa circunferencia (Fig. 5). Las propiedades de los ángulos en la circunferencia permiten concluir que ∠FBA + ∠FHA=180º = ∠FHA + ∠FHE, por lo que ∠FBA = ∠FHE =90º - ∠DEH=90º - ∠C, ya que DE es la paralela media relativa al lado BC en el triángulo ABC.
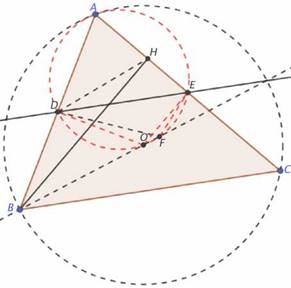
La segunda solución consiste en probar que: ∠C = ∠DOF. Las propiedades del circuncentro sugieren trazar los segmentos de mediatrices DO y EO, de donde se puede inferir que los puntos A, D, O y F pertenecen a la circunferencia de diámetro AO. Al trazar esta circunferencia todo parece indicar que también pasa por F. Las propiedades del triángulo rectángulo BHA permiten concluir que: ∠A = ∠DHA =180º - ∠DHE =180º - ∠DFE, debido a la simetría de la figura (Fig. 6). Esto prueba que F pertenece a la circunferencia de diámetro AO. Al igual que en la solución anterior ∠C = ∠DEA = ∠DEF = ∠DOF.
El tercer problema, elaborado por Sajidi, es el problema 2 de nivel avanzado de IGO (2018):
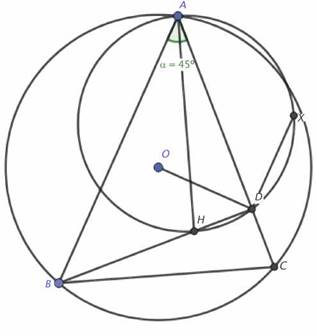
Sea ABC un triángulo acutángulo tal que ∠A = 45º y de circuncentro y ortocentro O y H, respectivamente. El punto D es el pie de la altura desde B. El punto X es el punto medio del arco AH del circuncírculo del triángulo ADH que contiene a D. Pruebe que DX = DO.
Luego de realizar los esbozos necesarios se pueden inferir los resultados siguientes: el triángulo HXA es isósceles y rectángulo en X por lo que ∠ADX = ∠AHX = 45º y además ∠COB = 2∠A = 90º (Fig. 7). Esto último implica que los puntos O y D pertenecen a una circunferencia de diámetro BC. Por ende, ∠ODA = 180º - ∠CDO = ∠OBC = 45º. Por tanto, AD es una bisectriz del ∠ODX y ∠ODX = 90º (Fig. 8) Además, si trazamos la altura desde C el triángulo que esta forma con los lados CA y AB sería isósceles y rectángulo, por lo que ∠ACH = 45º = 1/2∠AXH. Esto, unido al hecho de que AX = XH, implica que X es el circuncentro del triángulo ACH y, por tanto, AX = XH = XC. Luego, OX es mediatriz del lado AC, por lo que OX ⊥ AD (Fig. 9). Finalmente, AD es bisectriz del ∠ODX y AD ⊥ OX, lo cual se traduce en que el triángulo ODX es isósceles y OD = DX.
CONCLUSIONES
La resolución de problemas constituye el eje central de la asignatura Matemática. Por lo que resulta importante el conocimiento de las herramientas heurísticas que posibilitan la solución de un problema. En este sentido, este artículo ha estado dirigido a la importancia de las construcciones geométricas en el proceso de resolución de problemas y se muestran tres construcciones a realizar en tres problemas de las olimpiadas iraníes de geometría, lo que constituye una valiosa herramienta para un profesor que entrene estudiantes de concursos y olimpiadas de matemáticas.