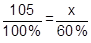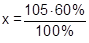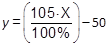INTRODUCCIÓN
Una de las asignaturas más importantes para la formación de los estudiantes es la Matemática, debido a que es una ciencia indispensable tanto para la vida cotidiana como en el desempeño profesional de cualquier disciplina. Para nadie constituye un secreto que su aprendizaje es de gran dificultad y sobre todo la resolución de problemas y ejercicios que en ocasiones resultan sencillos, pero que representan gran dificultad para los que no los saben interpretar.
La matemática como disciplina, así como su enseñanza siempre han tenido como finalidad, la resolución de problemas matemáticos. Según René Descartes “Cada problema que resolví se convirtió en una regla que más adelante me sirvió para solucionar otros problemas”. Cada día se hace más patente la falta de esta regla de la que se habla anteriormente. Construir una teoría de la resolución de problemas de matemáticas dentro de la que puedan ser interpretados y evaluados la inmensa cantidad de trabajos empíricos que sobre este tema se publican.
El principal precursor de esta teoría es George Pólya, para él la resolución de problemas ha de ser un arte donde la reproducción del profesor y la práctica ayuda a interiorizar en un proceso sencillo y accesible resolver problemas. Pólya nació en Hungría en 1887. Obtuvo su doctorado en la Universidad de Budapest y en su disertación para obtener el grado abordó temas de probabilidad. Fue maestro en el Instituto Tecnológico Federal en Zúrich, Suiza. En 1940 llegó a la Universidad de Brown en estados Unidos y pasó a la Universidad de Stamford en 1942. En sus estudios estuvo interesado en el proceso del descubrimiento o cómo es que se derivan los resultados matemáticos. Señaló que para la comprensión de una teoría se debe conocer cómo fue descubierta. Por ello su enseñanza enfatizaba el proceso de descubrimiento aún más que simplemente desarrollar ejercicios adecuados. Se considera que fue el que popularizó el término “método heurístico” en su libro How to solve it.
Respecto a este método se puede decir que consiste en un conjunto de estrategias basadas en la experiencia, la práctica y la observación que permiten una solución eficiente de un problema. La palabra proviene del griego εὑρίσκω y significa hallar o encontrar. Se puede señalar que la realidad escolar permite evidenciar las dificultades que presentan los estudiantes, cuando se les enuncian problemas matemáticos en los cuales deben transcribir situaciones de la cotidianidad y del contexto a lenguaje matemático (modelación), plantear y resolver ecuaciones, por lo que en la búsqueda para contribuir a que los estudiantes mejoren en este aspecto, se plantea actualizar el tema de resolución de problemas matemáticos con una didáctica y el uso de Microsoft Excel como elemento motivador en la solución de un problema de porcientos.
DESARROLLO
Desde tiempos muy remotos, los científicos comenzaron a tratar de entender y enseñar habilidades necesarias para resolver problemas matemáticos. Considera Delgado (1999) que su desarrollo está dividido en dos etapas bien delimitadas por el surgimiento de los trabajos de Pólya en 1945. En la primera etapa se abarca el período de la antigüedad hasta 1945. En esta etapa se destaca el trabajo realizado por el filósofo griego Sócrates que se encuentra principalmente en el Diálogo de Platón, obra donde el autor se dirigió a un esclavo por medio de preguntas para la solución de un problema: la construcción de un cuadrado de área doble a la de un cuadrado dado, por medio del uso de un conjunto de estrategias, técnicas y contenido matemático aplicado al proceso de resolución.
En 1637 es publicado el Discurso del Método obra realizada por el matemático, físico y filósofo francés René Descartes, quién señalaba lo que se ha dado llamar “modelos del pensamiento productivo” o “consejos para aquellos que quisiesen resolver problemas con facilidad”, estos consejos aún en la actualidad resultan beneficiosos. Se considera que otro de los impactos significativos en la teoría de resolución de problemas fue el aporte realizado por el matemático suizo Leonard Euler, que al exponer muchos de sus resultados incluyó reflexiones sobre las técnicas que utilizó y, por otro lado, se ocupó de la educación heurística de sus discípulos.
El segundo periodo está delimitado desde el 1945 hasta el momento actual, surge con la aparición de los trabajos de Pólya, principalmente con su obra How to solve it, que constituye un inmenso aporte y se ha convertido en referencia obligada para todos los investigadores que, con posterioridad, se han dedicado al estudio de este tema. Más tarde Pólya publica dos importantes obras: Mathematical and Plausible Reasoning (1954) y Mathematical Discovery (1965). Otro paso importante de esta segunda etapa es la vuelta hacia lo básico como salida a la crisis planteada por la “Matemática moderna”, la cual según Schoenfeld (1985), convierte la resolución de problemas en el eje central de las Matemáticas de la década de los años setenta.
En la década de los años ochenta se destacan los trabajos del profesor Allan Schoenfeld, quien estudia y critica el método heurístico de Pólya, perfeccionándolo en buena medida, al crear subestrategias más accesibles al trabajo con los estudiantes. Este autor, que ha develado cuatro categorías del conocimiento y comportamiento necesarias para caracterizar adecuadamente las formas de solucionar problemas, publica en 1985 su obra más importante: Mathematical Problem Solving.
Estas categorías consisten en:
Dominio del conocimiento: incluye definiciones, hechos y procedimientos usados en el dominio matemático. Concebir un plan: el problema debe de relacionarse con problemas semejantes, relacionarse con resultados útiles. Estrategias cognoscitivas: incluye métodos heurísticos tales como descomponer el problema en simple casos, establecer metas relacionadas, invertir el problema y dibujar diagramas.
Estrategias cognoscitivas: incluye métodos heurísticos tales como descomponer el problema en simple casos, establecer metas relacionadas, invertir el problema y dibujar diagramas.
Estrategia metacognoscitiva: se relaciona con el monitoreo empleado al resolver el ejemplo del proceso de selección de una estrategia y la necesidad de cambiar de dirección como resultado de una evaluación permanente del proceso.
Sistemas de creencias: incluye las ideas, que los estudiantes tienen acerca de la matemática y cómo resolver el problema.
Según Juídias Barroso y Rodríguez Ortiz (2007) se muestran los diferentes métodos de resolución de problemas y sus diferentes características (Tabla 1).
Tabla 1 Métodos de resolución de problemas
| Autor | Primera fase | Segunda fase | Tercera fase | Cuarta fase |
|---|---|---|---|---|
| Pólya (1945) | Comprensión del problema | Planificación | Ejecución del plan | Supervisión |
| Dunlap y McKnight (1980) |
Percepción de símbolos escritos Decodificación de símbolos escritos Formulación del significado general de las oraciones Traducción del mensaje general en un mensaje matemático |
Determinación de lo que hay que buscar Examen de los datos relevantes Análisis de las relaciones entre los datos Elección de las operaciones matemáticas Estimación de las respuestas |
Formulación de los datos mediante la notación matemática Ejecución de los cálculos matemáticos Decodificación de los resultados para que tengan sentido técnico Formulación de los resultados técnicos como respuestas a las cuestiones iniciales |
Verificación de las respuestas |
| Gagné (1983) | Traducción verbal de las situaciones descritas al lenguaje matemático | Fase central de cálculo | Validación de la solución | |
| Montague (1988) |
Lectura del problema Paráfrasis Visualización Enunciado del problema |
Hipótesis Estimación |
Cálculo | Verificación |
| Schoenfeld (1979) |
Análisis Exploración |
Diseño | Implementación | Verificación |
| Uprichard, Phillips y Soriano (1984) |
Lectura Análisis |
Estimación Traducción |
Cálculo | Verificación |
| Mayer (1991) |
Representación Traducción Integración |
Planificación |
Monitorización Ejecución Verificación |
Verificación |
| Garofalo y Lester (1985) | Orientación | Organización | Ejecución | Verificación |
| Glass y Holyak (1986) | Comprensión o representación del problema | Planificación | Ejecución del plan | Evaluación de los resultados |
| Brandsford y Stein (1984) |
Identificación Definición |
Exploración | Actuación |
Observación Aprendizaje |
Según las líneas directrices afines a las habilidades y capacidades que deben alcanzar los estudiantes de séptimo grado se hace necesario (Domínguez Escobar et al., 2016):
Adiestramiento lógico-lingüístico:
Modelar.
Utilizar recursos para la racionalización del trabajo mental y práctico.
Formular y resolver problemas.
Las razones antes expuestas permitieron realizar esta didáctica, con el uso del método heurístico.
Resuelve el siguiente ejercicio
Esteban ya ganó 50 de 75 juegos contra su computadora. Si quiere efectuar en total 105 juegos. ¿Cuántos juegos más tiene que ganar para que al final de la jornada le haya ganado a su computadora el 60% de los juegos?
Argumenta cómo a través de este ejercicio se potencia el desarrollo del pensamiento creativo con fantasía.
|
P: Enunciar los datos que nos proporciona el problema P: ¿Que tipo de problema es? P: Muy bien, en función de los datos cómo presentamos la operación a realizar. Invita a algún alumno a resolverlo en la pizarra mientras que los restantes realizan sus operaciones de forma individual P: Alguno puede decirnos cuáles son los datos del problema y qué nos falta por hallar P: ¿Están de acuerdo con los resultados, alguien no concuerda? En caso de existir algún alumno que no alcanzó el mismo resultado, explicará el procedimiento que realizó para que logre identificar su error en las operaciones realizadas |
Datos: Total de juegos = 105 Juegos Ganados = 50 Juegos realizados = 75 Porciento = 60 % ¿Cuantos juegos más tiene que ganar para llegar al 60 %? El estudiante a partir de los datos determina que es un problema de cálculo porcentual Debemos hallar cuantos juegos es el 60 % Cantidad de juegos para llegar al 60 % Ahora hemos encontrado que el 60 % de los juegos es 63 Pero nos interesa saber cuánto le faltaría por ganar y así poder llegar al 60 %. ¿Si el ya ganó 50 juegos? Esto nos lleva a encontrar la diferencia entre 63 juegos y los 50 juegos ganados: 63 - 50 = 13 Respuesta: Esteban debe ganar 13 juegos |
Profesor: ¿Qué otra respuesta se puede derivar del ejercicio dado y resuelto?
Estudiante: Se pueden crear diferentes escenarios, para ello podemos variar los porcientos de juegos:
Al convertir porciento a tanto por uno se determina que es la ecuación de una línea recta con pendiente 105.
y = 105·x - 50
| Total juegos | Juegos ganados | |
|---|---|---|
| 105 | 50 | |
| 1 | 60,.00% | 13 |
| 2 | 80,00 % | 34 |
| 3 | 100,00 % | 55 |
CONCLUSIONES
Uno de los aspectos principales en la enseñanza de la Matemática es la resolución de problemas. El maestro puede usarlo para perfeccionar el pensamiento matemático, no obstante, los docentes trabajan con una cansona monotonía y una mecánica anquilosante los ejercicios y problemas, y en muchas ocasiones sin ninguna aplicación práctica en la vida cotidiana. Esto provoca una desmotivación en el proceso cognoscitivo. A juicio del autor es importante el conocimiento de las diferentes estrategias de resolución de problemas, crear enunciados creativos y variados, y que además constituyan un desafío para los estudiantes. Por otra parte, se hace necesario el uso de herramientas didácticas que propicien la visualización y creatividad en su solución.
Decía el gran músico y compositor afroamericano Duke Ellington: “Los problemas son oportunidades para demostrar lo que se sabe”.