Mi SciELO
Servicios Personalizados
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Minería y Geología
versión On-line ISSN 1993-8012
Min. Geol. vol.33 no.4 Moa oct.-dic. 2017
ARTÍCULO ORIGINAL
Modelo matemático de fragmentación para la trituración por impacto de las zeolitas de San Andrés, Holguín (Cuba)
Mathematical model of fragmentation for the impact crushing of the zeolites of San Andrés, Holguín (Cuba)
José Ramón Echevarría Pérez1, Alfredo Lázaro Coello Velázquez2, Juan María Menéndez Aguado3
1Doctor en Ciencias Técnicas. Profesor Auxiliar. Universidad de Holguín "Oscar Lucero Moya". Holguín, Cuba jhperez@facing.uho.edu.cu
2Doctor en Ciencias Técnicas. Profesor Titular. Instituto Superior Minero Metalúrgico de Moa, Holguín, Cuba acoello@ismm.edu.cu
3Doctor en Ciencias Técnicas. Universidad de Oviedo. España maguado@uniovi.es
RESUMEN
La modelación matemática con ayuda de los métodos de balance de población de partículas resulta imprescindible cuando se trata de la evaluación de los procesos y eventos de fracturas que tienen lugar en la trituración por impacto. Con el propósito de valorar la influencia de la energía de fragmentación y la razón de alimentación a la trituradora en las funciones de clasificación y de distribución de la fragmentación se propone un modelo basado en la combinación en serie de los modelos estructurales de Reid (1965) y Whiten (1972) modificado, que incluyen las expresiones de Vogel y Peukert (2005) y Austin y Luckie (1972). La validación del modelo combinado se realizó utilizando las técnicas estadísticas de Chi-cuadrado y los gráficos cero errores. Los resultados del trabajo demuestran que el modelo propuesto simula con adecuada precisión la fragmentación en la trituración por impacto. La función de probabilidad de fragmentación de la roca zeolítica depende de las condiciones de operación cuya sensibilidad se ve afectada por la energía de impacto. La función de distribución del tamaño no depende de las condiciones de operación. La distribución de tamaño del producto se ve severamente afectada por la energía de impacto, siguiendo las mismas regularidades de la función de clasificación.
Palabras clave: funciones de fractura; modelación matemática; métodos de balance de población de partículas; trituración por impacto; zeolitas.
ABSTRACT
Mathematical modeling based on particles population balance method is a useful tool for impact crushing valuation. With the objective to evaluate the impact energy and feed rate influence on classification and fragmentation distribution functions, is proposed a mathematical model based on serial combination of Reid (1965) and Whiten (1972) structural models, that include Vogel and Peukert (2005), and Austin and Luckie (1972) mathematical expressions. Model validation was done using Chi-square statistical technique and zero-error graphic. The results show that proposed model simulate with adequate accuracy the impact crushing fragmentation process. The probability function of zeolite rock from San Andrés ore depend on the operation conditions witch sensibility was affected by impact energy. Fragmentation distribution function do not depend on the energy impact variation, while particle size distribution was affected by impact energy varying according to classification function tendency
Keywords: fracture functions; mathematical modeling; particle population balance methods; impact crushing; zeolites.
1. INTRODUCCIÓN
En la actualidad las trituradoras de impacto son ampliamente utilizadas en las operaciones de conminución gracias a su alto grado de reducción, la flexibilidad granulométrica de los productos y su diseño sencillo (Nikolov 2002).
Es comúnmente reconocido el empleo de la modelación y simulación en la predicción del comportamiento de las plantas de procesamiento de minerales con fines de ahorro energético, reducción de los costos generales y el análisis y optimización de los circuitos de trituración y molienda (King 2012; Coello et al. 2011).
La práctica de la modelación por los métodos basados en el balance de población de partículas cuenta con varios modelos que describen el proceso de fragmentación de minerales con una adecuada precisión y exactitud. Los más extendidos son el modelo de Reid (1965) y el de Whiten (1972). El primero considera la fragmentación de partículas como un acto simple de fragmentación; mientras que el segundo supone que las partículas de material dentro de la trituradora pueden someterse a más de un ciclo de fragmentación o pasar a través del proceso sin romperse (Leyva et al. 2015). El modelo de fragmentación simple de Reid (1965) aparece en la ecuación (1):
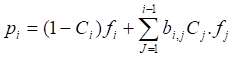 (1)
(1)
La ecuación (2) representa el modelo de fragmentación de Whiten (1972):
![]() (2)
(2)
Particularmente para la trituración de impacto existen algunos reportes a considerar en su estudio (Nikolov 2002, 2004; Shi et al. 2003; Vogel y Peukert 2005).
El modelo de Nikolov (2002, 2004) toma como punto de partida el modelo estructural de Whiten (1972) e incluye, en lugar de la ecuación de la función de clasificación, la distribución de Weibull acumulativa. La naturaleza de la trituración por impacto permite obtener un producto de un rango de tamaño más amplio que las trituradoras de cono y de mandíbulas.
Intentando resolver las limitaciones de la expresión de la función de clasificación propuesta por Attou, Clepkens y Gustin (1999), Nikolov y Lucio (2002) para la modelación de la trituración por impacto, utilizaron la siguiente ecuación, asumida por Nikolov (2002) en su modelo:
![]() (3)
(3)
A juzgar por las características de los parámetros de la función de clasificación de Nikolov y Lucio (2002), al estar basado en la distribución de Weibull, potencialmente puede cubrir con mayor precisión el rango de tamaño producido en la trituración por impacto.
Por su parte, Vogel y Peukert (2005) proponen un modelo de fragmentación que, siendo matemáticamente más sencillo que el modelo de Shi y demás investigadores (2003), representa la fragmentación múltiple como un resultado de la repetición en n ciclos del modelo de fragmentación simple de Reid (1965). Esto supone que todas las partículas minerales tienen las mismas oportunidades de fragmentación, algo verdaderamente poco probable. Es archiconocida la dependencia de la probabilidad de fragmentación del tamaño de las partículas minerales.
A diferencia de la expresión usada por Nikolov para la función de clasificación Vogel y Peukert (2005) emplean una ecuación que considera no solo el tamaño de las partículas minerales (xj), sino la resistencia a la fragmentación del mineral (coeficiente fmat) y la energía cinética de impacto para la fragmentación (E-Emin). E- es la energía cinética del rotor del triturador y Emin – es el límite de la energía cinética por debajo del cual no ocurre la fragmentación de la partícula mineral con tamaño (xj). En este sentido, la ecuación presentada por Vogel y Peukert (2005) articula las variables operacionales con la función de clasificación.
Las trituradoras de impacto se diferencian substancialmente del resto. En el caso específico de las trituradoras de cono y de mandíbulas, el proceso de la fragmentación es relativamente lento. Sin embargo, en la trituración por impacto, el proceso de fragmentación ocurre particularmente rápido, provocando que la formación y propagación de las fisuras magistrales, a partir de los defectos naturales de las partículas minerales, sea extremadamente dinámica, propia de la fractura por estadillo.
Esta dinámica se expresa en las trituradoras de impacto por su elemento distintivo: el rotor. Este elemento mecánico es responsable de la fragmentación por impacto de las partículas minerales. En los trituradores de eje vertical (vertical axis crusher), las partículas son alimentadas al rotor horizontal (horizontal turning table) con guías radiales y así son proyectadas por las fuerzas centrífugas contra las paredes del triturador.
En el caso de los trituradores de martillo, la fragmentación ocurre en la periferia del rotor y las paredes de las trituradoras por la interacción martillo-partícula. Es importante señalar que el tamaño del rotor es incomparablemente mayor que las partículas minerales. Esto hace que la energía cinética asociada al rotor sea mucho más importante que la propia velocidad de las partículas minerales en su proyección hacia las paredes del triturador. Esta energía cinética del rotor fue considerada por Attou, Clepkens y Gustin (1999) y Nikolov (2002) como la energía de impacto por unidad de masa.
Otro elemento que distingue a estas trituradoras es la posibilidad de regulación del tamaño del producto triturado. Según los reportes de Shi et al (2003) y de Vogel y Peukert (2005), la influencia de esta variable en la trituración por impacto resulta de notable significación.
Considerando estas particularidades de la trituración por impacto, el objetivo de presente artículo es, mediante la combinación en serie de los modelos de Reid (1965) y Whiten (1972), exponer la influencia en las funciones de clasificación y de distribución de la fragmentación de la energía de impacto y productividad de la alimentación.
2. MATERIALES Y MÉTODOS
2.1. Descripción del modelo
Como punto de partida para la modelación de la trituración por impacto de las zeolitas de San Andrés, Holguín (Cuba) se ha tomado un modelo que combina la fragmentación en serie de los modelos estructurales de fragmentación de Reid (1965) y de Whiten (1972) modificado. Este modelo aparece representado en la ecuación 4.
![]() (4)
(4)
En la ecuación (1) el parámetro f (matriz de alimentación) es substituida por p en el modelo de fragmentación de Reid (1965).
I= es la matriz de identidad.
C1= función de clasificación en el modelo de fragmentación de Reid, u.
B=función de distribución de la fragmentación, u.
2.2. Parámetros del modelo
2.2.1. Función de distribución de la fragmentación
Según Kelly y Spottiswood (1990) existen dos esquemas conceptuales sobre la función de distribución de la fragmentación: uno considera que esta función es independiente de tamaño inicial; la otra requiere de la determinación de dicha función para cada clase inicial. Ambos conceptos son empleados ampliamente en la modelación de los procesos de reducción con la debida precisión (Leyva et al. 2015). La ecuación de Austin y Luckie (1972) usualmente es considerada como la más adecuada a la trituración por impacto (Nikolov 2004; Coello et al. 2011).
![]() (5)
(5)
B(i,j) = 0 para i > j
Donde:
B(i,j) = Fracción de masa de tamaño i obtenida de la fragmentación de las partículas de tamaño j;
F: Fracción de masa de partículas finas, unidades;
xi: es el tamaño de las partículas del intervalo i producto de la fragmentación de las partículas j, mm;
xj: Tamaño promedio de las partículas originales en el intervalo de tamaño j, mm;
α y β: son coeficientes adimensionales que caracterizan la forma de la distribución de las fracciones finas y gruesas del material;
2.2.2. Función de clasificación
Los modelos empleados por Nikolov (2002) y por Vogel y Peukert (2005) fueron evaluados por Coello y demás investigadores (2011) mediante el ajuste a los datos experimentales de Datta (1999). En este sentido, el ajuste del modelo de la función de clasificación de Nikolov y Lucio (2002) no fue el esperado. Considerando estas razones y las oportunidades que brinda la función de clasificación de Vogel y Peukert (2005) condujeron a la selección.
La expresión de Vogel y Peukert (2005) se expone en la ecuación 6.
![]() (6)
(6)
2.3. Experimentos
La roca zeolítica en calidad de monoclase, de tamaño de 4-6 mm, fue alimentada a una trituradora de martillos de laboratorio con un rotor de 0,1 m de velocidad variable de 1 500 rpm, 2 750 rpm y 3 100 rpm desde una tolva de 0,1 m3. El rotor dispone de cuatro filas de martillos de tipo estribo.
La energía cinética de impacto fue calculada por la fórmula de Attou, Clepkens y Gustin (1999) que aparece en la ecuación (7).
![]() (7)
(7)
Donde:
E: energía de impacto, J/kg;
R: radio del rotor (m);
Hb: altura de la superficie de impacto de los martillos (m);
ω : velocidad angular (1/s).
Se realizaron dos series de ensayos. En la primera se simula la fragmentación simple por el modelo de Reid (1965) y la segunda simula la fragmentación múltiple por el modelo de Whiten.
En la primera serie se variaron dos parámetros en la trituradora: la velocidad del rotor en los tres niveles posibles que corresponden a los valores de E de 100 J/kg, 275 J/kg y 450 J/kg y la capacidad de alimentación en 0,6 t/h; 1,3 t/h y 2,3 t/h.
La función de clasificación se determinó según Vogel y Peukert (2005), que simula la fragmentación simple usando la trituradora sin rejilla de control. Considerando que el producto alimentado es una monoclase la función de clasificación se determinó de forma experimental por la fórmula 8.
![]() (8)
(8)
Donde:
Cj : Función de clasificación experimental, u;
Mj: Masa del producto de la trituradora cernido, g;
M: Masa total del producto, g.
A partir de los valores de Cj, obtenidos experimentalmente, se obtuvieron los parámetros del modelo de Vogel y Peukert (2005): xj, Emin y fmat.
Considerando que el producto alimentado es una monoclase, entonces, fj = 1 y fi= 0; por ende, la función de distribución de la fragmentación puede ser determinada por la fórmula 9:
![]() (9)
(9)
Los intervalos i y j se muestran en la Tabla 1.

En la segunda serie las partículas del producto (pi) obtenido por fragmentación simple son alimentadas a la fragmentación múltiple descritas por el modelo de Whiten (1972) para ocho combinaciones diferentes de valores de: energía cinética (E), flujo de alimentación (Q) y regulación de salida del producto (S). Los valores de las variables fueron: Q = 0,3 y 2,3 t/h; E = 100 y 450 J/kg para dos tamaños de abertura de la rejilla de control del triturador (d= 3 mm y 6 mm).
3. RESULTADOS Y DISCUSIÓN
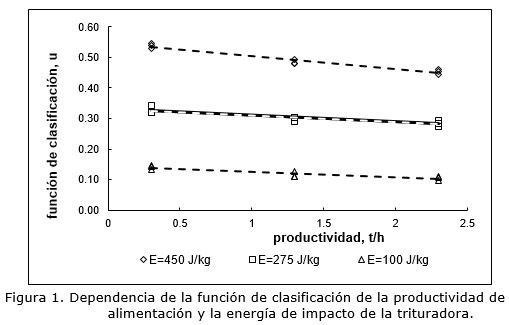
Considerando las regularidades presentadas de la Figura 1, la probabilidad de fragmentación de las partículas minerales depende de las condiciones de operación.
Con el incremento de la productividad esta función se inclina ligeramente hacia su disminución. El efecto de la energía de impacto se muestra mucho mayor que la productividad de alimentación. Así lo confirma el tratamiento de los resultados experimentales con el software StatGraphics 5.1 (Tabla 2). Regularidades similares son reportadas por Coello y demás investigadores (2011). Nikolov (2004) cita que el incremento de la productividad del triturador incide en la disminución de la probabilidad de fragmentación.
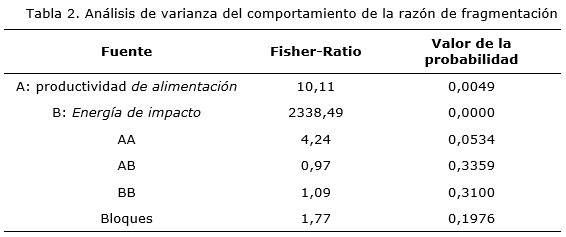
A juzgar por la Figura 2, la influencia de la variación de la energía de impacto del rotor de la trituradora sobre la función de distribución de la fragmentación es poco definida, aunque existen diferencias notables en los niveles de la energía de impacto.
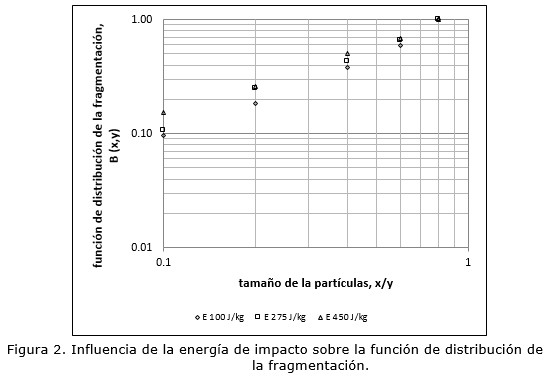
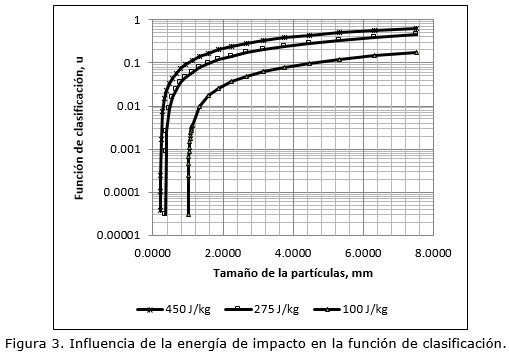
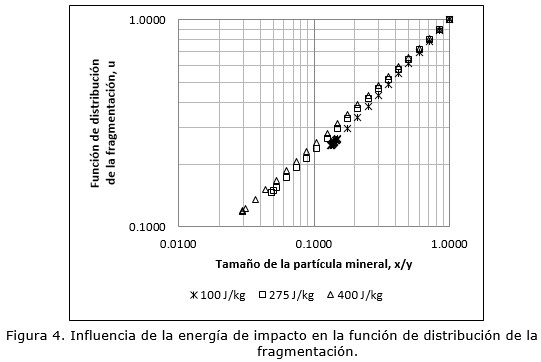
Considerando los valores de los parámetros de la función de Vogel y Peukert (2005), obtenidos para la roca zeolítica de San Andrés (Holguín, Cuba) (xj. Emin = 0,1 J m/kg y fmat = 0,302 kg /Jm), fueron simuladas las funciones de clasificación y de distribución de la fragmentación (Figuras 3 y 4).
La probabilidad de fragmentación de la partícula mineral está sujeta a la variación de la energía de impacto del rotor de la trituradora. En este sentido, un incremento de esta última conlleva al incremento notable de los valores de la función de clasificación.
No es posible demostrar que la variación de la energía de impacto del rotor de la trituradora provoque una variación apreciable de la función de distribución de la fragmentación. En el concepto original de esta función (Epstein 1948) no se debe a las condiciones operacionales, sin embargo, en los equipos reales la re-fragmentación de la progenie es algo verdaderamente probable. Kelly y Spottiswood (1990) enfatizan que el concepto de fragmentación simple deja de ser válido en condiciones de fragmentación donde la intensidad de la energía sea alta. Los valores del coeficiente m (0,6-0,9) hablan sobre la prevalencia de la fractura por estallido frente al clivaje.
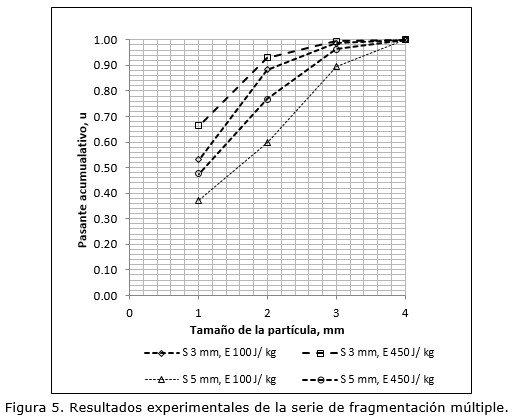
En la Figura 5 aparecen los resultados experimentales para la segunda serie de experimentos de la fragmentación múltiple. A juzgar por los resultados, se conserva la misma regularidad de la curva del pasante acumulativo para las diferentes condiciones de operación, correspondiendo a la energía de impacto un efecto positivo sobre la fineza del producto triturado; mientras que el tamaño de la rejilla impone un efecto similar, o sea, en tanto mayor es el tamaño de la rejilla, más grueso es el producto de la trituración.
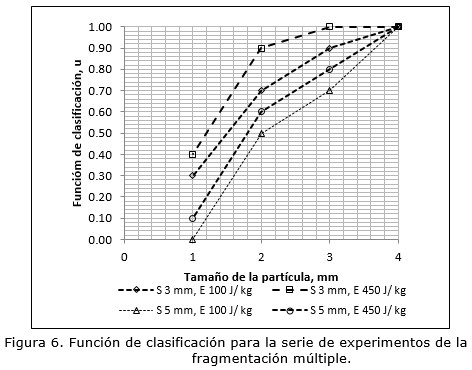
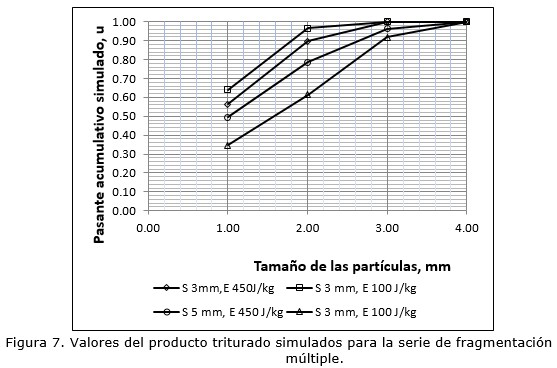
Los valores de la función de clasificación muestran una dependencia de las condiciones de operación similar a la regularidad observada del pasante acumulativo. Los valores simulados del pasante acumulativo del producto triturado (pi), usando el modelo de la ecuación 4, aparecen en la Figura 7. A juzgar por estos resultados, la forma de la distribución de tamaño de ambos productos es bastante similar, siendo consecuentes las variaciones en dependencia de la energía de impacto.
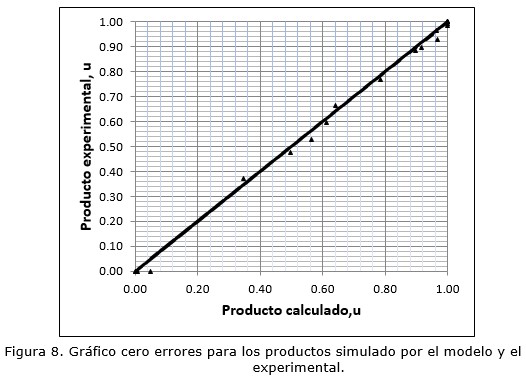
La reproducibilidad del modelo propuesto se pone de manifiesto en el valor del error de estimación (0,02 %) y los resultados de la prueba de Chi-cuadrado, cuyo valor calculado (0,0045) es mucho menor que su valor crítico para 95 % de probabilidad. El gráfico cero errores (Figura 8) confirma esta valoración.
Finalmente, los resultados confirman la hipótesis de que, en el triturador de martillo, las partículas minerales, probablemente, en un primer momento reciban el impacto con los martillos que debe producir una primera fragmentación. Luego del primer impacto son lanzadas a cierta velocidad contra las paredes revestidas de la carcasa donde debe recibir una segunda fragmentación que puede convertirse en múltiples fragmentaciones.
4. CONCLUSIONES
· Se demuestra que la combinación en serie de los modelos de Whiten (1972) y Reid (1965) simula con adecuada precisión la trituración por impacto de la roca zeolítica de San Andrés en diferentes condiciones de operación, variando la productividad y la energía de impacto de la trituradora.
· La probabilidad de fragmentación de la roca zeolítica depende de las condiciones de operación; su sensibilidad a estos cambios se expresa por una alta dependencia de la energía de impacto. En tanto, la función de distribución de la fragmentación para esta roca se mantiene prácticamente inalterable al variar las condiciones de operación del triturador. Se evidencia que la variación de la granulometría del producto triturado opera según las regularidades de la función de clasificación.
5. REFERENCIAS
Attou, A.; Clepkens, O. y Gustin, R. 1999: Modélisation de la fragmentation de matière solide dans un concasseur à chocs à axe horizontal. CTP Report TP 909: 19-28.
Coello, A. L.; Menéndez, J. M.; Hechavarría, J. R.; Sánchez, A. B. y Álvarez, B. 2011: Toward the determining eh behavior of de fragmentation functions during the impact crushing of minerals. Mineral and metallurgical processing 28(2): 82-86.
Epstein, B. 1948: The mathematical description of certain breakage mechanisms leading to the logarithmic-normal distribution. Journal of the Franklin Institute 244(6): 471-477.
Kelly, E. G. y Spottiswood, D. J. 1990: The breakage function, what is it really? Minerals Engineering 3(5): 405-414.
King, R. P. 2012: Modelling and simulation of mineral processing Systems. 2 ed. Schneider, C. L. y King, E. A. (editors). Elsevier, 403 p.
Leyva, A.; Coello, A. L.; Hechavarría, J. R.; Menéndez, J. M.; Leyva, O. S. y Leyva, E. 2015: Modelo de Whiten (1972) modificado para modelación de la trituración de la antracita residual de Nicaro. Minería y Geología 31(1): 13-28.
Nikolov, S. 2002: A performance model for impact crusher. Minerals Engineering 15(10): 715–721.
Nikolov, S. 2004: Modelling and simulation of particle breakage in impact crushers. International Journal of Mineral Processing 74: 219–225.
Reid, K. J. 1965: A solution to the batch grinding equation. Chemical Engineering Science 20(11): 953-963.
Shi, F.; Kojovic, T.; Esterle, J. S. y David, D. 2003: An energy-based model for swing hammer mills. International Journal of Mineral Processing 71(1): 147–166.
Vogel, L. y Peukert, W. 2005: From single particle impact behaviour to modelling of impact mills. Chemical Engineering Science 60(18): 5164–5176.
Whiten, W. J. 1972: The simulation of crushing plants with models developed using multiple spline regression. Journal of the South African Institute of Mining and Metallurgy 72(10): 257.
Recibido: 09/07/2017
Aprobado: 26/09/2017
José Ramón Hechavarría Pérez, Doctor en Ciencias Técnicas. Profesor Auxiliar, Universidad de Holguín Oscar Lucero Moya Holguín, Cuba jhperez@facing.uho.edu.cu














