Mi SciELO
Servicios Personalizados
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Revista Ciencias Técnicas Agropecuarias
versión On-line ISSN 2071-0054
Rev Cie Téc Agr vol.23 no.4 San José de las Lajas oct.-dic. 2014
ARTÍCULO ORIGINAL
Modelo para el cálculo de la resistencia del suelo a la penetración de sondas. Parte I: sondas cónicas
Model for calculation of soil resistance to probes penetration. Part I: Conical probes
M.Sc. Ernesto Ramos Carbajal, Dr.C. Arturo Martínez Rodríguez, Dr.C. Armando García de la Figal Costales
Universidad Agraria de La Habana. Facultad de Ciencias Técnicas. Centro de Mecanización Agropecuaria. San José de las Lajas, Mayabeque, Cuba.
RESUMEN
La sonda de punta cónica constituye la base de comparación para el diseño de cualquier otro tipo de sonda. Un modelo teórico conceptual de la interacción con el suelo de una sonda de punta cónica destinada al sensoramiento de la resistencia a la penetración del suelo, se expone en el presente trabajo. El modelo, elaborado a partir de un análisis cuasi-estático del sistema de fuerzas que actúa sobre la sonda, tiene en cuenta las dimensiones y forma geométrica del cono, así como propiedades físico-mecánicas tales como: el coeficiente de fricción suelo/metal y la tensión de fallo del suelo. Como resultado de la evaluación del modelo, con datos de entrada procedentes de la determinaciones experimentales, se obtiene que, tanto la fuerza de penetración, como la resistencia a la penetración (índice de cono) calculados, se ven incrementadas con el aumento del ángulo del cono. La comparación de la resistencia a la penetración calculada mediante el modelo, evaluado con los datos geométricos correspondientes a un cono normalizado ASAE, con resultados experimentales obtenidos en un suelo Ferralítico Rojo, arrojó un error de predicción de 2,8%.
Palabras clave: modelo, resistencia a la penetración, modelo teórico conceptual.
ABSTRACT
The conical probe tip provides a comparison basis for the design of any other probe tip. A conceptual theoretical model of the soil-probe interaction of a conical probe tip, designated to sensing of soil penetration resistance, is presented. The model, elaborated from a quasi-static analysis of the system of forces acting on the probe, takes into account the dimensions and geometric form of the cone, as well as physical-mechanical properties such as: the soil/metal coefficient of friction and the soil compression strength. As a result of the model evaluation, with input data taken from experimental determinations, the predicted penetration force and the calculated penetration resistance (cone index), increases with the increment of the cone angle. The comparison of the predicted penetration resistance, evaluating the model with geometric data corresponding to a normalized ASAE cone, with experimental results obtained in a Red Ferralitic Soil, produced a prediction error of 2,8%.
Key words: model, penetration resistance, conceptual theoretical model.
INTRODUCCIÓN
Dentro de los factores que mayor incidencia tienen en los rendimientos de los cultivos se destacan los relacionados con las propiedades del suelo. En función de esto, ya desde finales del siglo pasado se inicia el desarrollo de sensores capaces de determinar las diferentes propiedades del suelo de forma continua y en tiempo real, recolectando una amplia gama de mediciones de gran utilidad para el posterior manejo en sitio específico del suelo, garantizando su mejoramiento puntual y localizado (Owen et al., 1987; Stafford & Hendrick, 1988; Glancey et al., 1989).
Uno de los indicadores que mejor refleja las necesidades de laboreo de un suelo es su estado de compactación, el cual se ha venido estimando hasta ahora a través de la densidad aparente del suelo y/o de su resistencia a la penetración, medida con penetrómetros de punta cónica normalizados según ASAE (1991).
Numerosos investigadores y fabricantes han desarrollado sensores para la medición continua (On-the-Go) de las propiedades del suelo Sudduth et al. (1997); Adamchuk (2004); Hall & Raper (2005); Herrera et al. (2011); Hemmat et al. (2013). En función de los métodos de medición se han desarrollado una gran variedad de prototipos de sondas, siendo los más aceptados los que basan su principio de funcionamiento en la medición de resistencia mecánica del suelo, ya sea a una profundidad dada o en diferentes profundidades del perfil del suelo. Estas lecturas de la resistencia mecánica son utilizadas posteriormente para estimar la compactación del suelo.
Los factores que afectan la resistencia del suelo han sido identificados por diferentes investigadores Hettiaratchi & Reece (1974); Schuring & Emori (1964); Wismer & Luth, (1972); Andrade et al. (2008), Alihamsyah et al. (1990).
Asimismo han sido desarrollados diferentes modelos teóricos Johnson (2003); Chung & Sudduth, (2006); Chung et al. (2013;), empíricos Schuring & Emori (1964); Wismer & Luth (1972); Andrade- Sánchez et al., (2008) y de simulación por elementos finitos Shmulevich, (2010); Naderi-Boldaji et al. (2013), de la interacción sonda-suelo, dirigidos a esclarecer este proceso de interacción y poder relacionar la lectura de las sondas con el nivel de compactación del suelo bajo diferentes condiciones de humedad. Algunos de estos modelos empíricos no han podido ser validados en condiciones de suelos diferentes (Andrade et al., 2002, Mouazen et al., 2003a, Mouazen et al., 2003b, Mouazen & Ramos 2009; Lara, et al., 2013) y otros de naturaleza teórica conceptual presentan el inconveniente que tienen limitaciones para explicar la respuestas dinámicas del suelo durante la penetración de cono, en particular en condiciones de suelo heterogéneas debido la complejidad del análisis de equilibrio de fuerza (Shen & Kushwaha, 1998), así mismo los modelos analíticos aunque ayudando en la comprensión de las relaciones básicas, no consideran todos los detalles de una interacción de la herramienta del suelo (Chung & Sudduth, 2006); mientras que los modelos de simulación por elemento finito (FE) requieren, de códigos y algoritmos que no están disponibles por razones comerciales y de la disponibilidad de máquinas potentes con buenas prestaciones computacionales.
La sonda de punta cónica constituye una base de comparación para el diseño de cualquier otro tipo de sonda, ya que en la actualidad se emplean sondas cónicas normalizadas durante la medición de la resistencia a la penetración de los suelos a través del índice de cono (ASAE, 1991).
Un análisis del equilibrio de fuerzas en sondas de punta cónica permitirá la obtención de un modelo teórico conceptual que describa el proceso de interacción sonda-suelo. La comparación de los resultados de predicción que se obtengan sobre la base de la evaluación del modelo teórico, con resultados de mediciones experimentales de la resistencia a la penetración efectuados en investigaciones anteriores sobre un suelo Ferralítico rojo contenido en el Canal de Suelo del Centro de Mecanización Agropecuaria, constituirá un criterio inicial de validación del modelo para su aplicación en este tipo de suelo (Herrera et al., 2008; Ramos et al., 2012).
En el presente trabajo se expone un modelo obtenido a partir de análisis del equilibrio de fuerzas en una sonda de punta cónica destinada al sensoramiento de la resistencia a la penetración del suelo, el cual tiene en cuenta, no sólo parámetros geométricos, como pueden ser el ángulo del cono y sus áreas proyectadas, sino otras propiedades como el coeficiente de fricción suelo/metal y la tensión de fallo que puede tener lugar cuando dichos elementos se desplazan en el suelo durante el proceso de penetración.
MÉTODOS
Para el desarrollo del modelo se parte de la aplicación de las leyes del equilibrio de fuerzas de Newton que es procedente aplicar en este caso, ya que la sonda se traslada con velocidad constante.
El equilibrio de fuerzas es planteado sobre el diagrama de sólido aislado de una sonda cónica con parte cilíndrica cuya área de la base y longitud son constantes, mientras que se asigna como variable independiente el ángulo del cono.
Las ecuaciones emanadas de las ecuaciones de equilibrio de fuerzas son programadas en MathCad, versión 2000 Proffesional, obteniéndose los resultados en forma gráfica y tabulada.
Los datos experimentales sobre las propiedades del suelo, usados en la evaluación del modelo, así como en su validación, son tomados de experimentos anteriores, efectuados sobre ese mismo tipo de suelo (Ramos et al., 2012; Herrera et al., 2008).
RESULTADOS Y DISCUSIÓN
Equilibrio de fuerzas en una sonda de punta cónica destinada al sensoramiento de la resistencia a la penetración del suelo
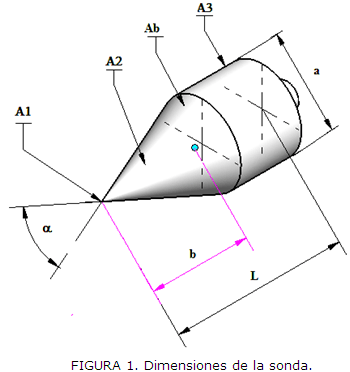
Dado el hecho de que el coeficiente de fricción entre dos superficies en contacto puede variar en función de la velocidad relativa entre dichas superficies, es necesario tener en cuenta este fenómeno durante el diseño de las sondas. Del mismo modo, durante la idealización de esta interacción se asume que la magnitud de las fuerzas normales que actúan sobre las superficies en enfrentamiento con el suelo, dependerá de la resistencia del suelo a ser deformado bajo una acción de compresión, lo cual se denota como la tensión de confinamiento (σ3) que correlaciona con el grado de compactación del suelo y por ende con su densidad volumétrica, considerado además que las sondas de diferente geometría, mantendrán la misma longitud (L) y la misma área de la base de la sonda al variar el ángulo Figura 1.
Las magnitudes asignadas a los diferentes términos que constituyen datos de entrada al modelo se relacionan a continuación:
Grosor de la punta: δ = 1,10-3 m;
Diámetro de la base del cono a:
![]()
a = 0,013 m
La longitud del cono más la parte cilíndrica se obtiene:

L= 0,024 m
Tensión de fallo de compresión según Herrera (2006):
= 1 3 = 0,2538´106 Pa
Coeficiente de fricción suelo/ metal según Ramos, et al. (2012): f=0,6
Tensión de corte:
![]()
Partiendo de estas consideraciones, a continuación se efectúan los análisis de la interacción suelo-herramienta, para el caso del cono:
Fuerzas que actúan sobre la sonda de punta cónica:
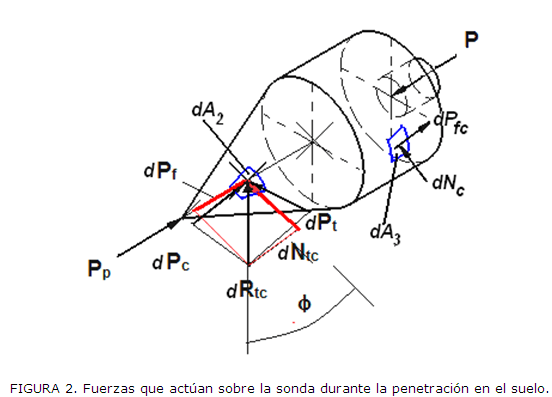
La Figura 2 muestra las fuerzas que actúan sobre las caras de la sonda de punta cónica durante su interacción con el suelo.
En el caso del cono durante su enfrentamiento al suelo, sobre la punta de grosor actúa la fuerza de resistencia frontal Pp, que no depende del ángulo y estará dada por la expresión. (4)
donde A1 es el área frontal y se determina como:
![]()
Sustituyendo (5) en (4) se obtiene que:

Evaluando para los datos declarados se obtiene:
PP= 0,199 N
De este modo sobre la superficie cónica actúa la resultante de las fuerzas de compresión Rtc, que resulta de la suma vectorial de la fuerza de compresión directa (Pc) en la dirección contraria al movimiento (considerado cuasi estático) y la componente de compresión en la dirección transversal Pt (Figura 2).
La fuerza de compresión frontal directa en la superficie cónica Pc se determinara como:
![]()
Siendo A2 el área de la superficie cónica y se determina como:
![]()
Sustituyendo la ecuación 8 en 7 se obtiene:
![]()
Mientras que Pt fuerza de compresión transversal en la superficie cónica se determina:
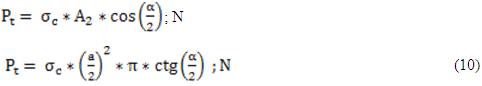
La fuerza normal (Ntc) que actúa sobre la superficie cónica está dada por:
![]()
Y la fuerza de fricción Pf sobre esta superficie será:
![]()
Sustituyendo la ecuación 11 en 12 se obtendra la fuerza de fricción que actúa sobre la superficie cónica:
![]()
En la superficie cilíndrica de área A3, actuará la fuerza de fricción Pfc, cuya normal estará dada por:
![]()
Siendo la fuerza de fricción:
![]()
Como quiera que la sonda se desplaza a una velocidad constante, es posible plantear el equilibrio de fuerzas en la dirección del movimiento, de manera que la fuerza total P, a la que se oponen las diferentes fuerzas de resistencia descritas, se obtiene mediante la sumatoria de fuerzas en la dirección del movimiento:
![]()
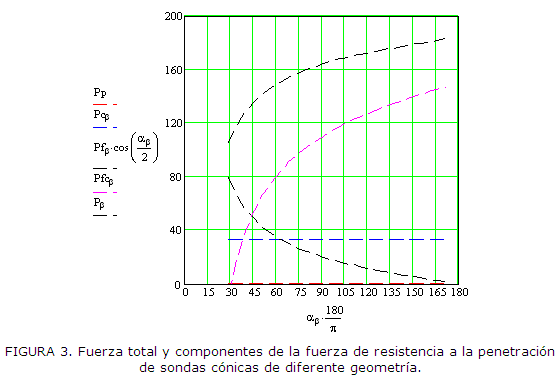
La evaluación del modelo, para un área de la base del cono de 130 mm2 y una longitud L de 24 mm, posibilitó obtener las magnitudes de la fuerza total de resistencia a la penetración de la sonda, así como sus diferentes componentes para diferentes ángulos del cono, lo cual se muestra en la Figura 3.
Como datos de entrada para la corrida del modelo se tomaron los valores de resistencia de fallo del suelo de 2,538 x 105 Pa correspondientes a un suelo ferralítico rojo obtenidos por Herrera et al. (2008), en ensayos triaxiales para una densidad aparente de 1,1 g/cm3 y humedad de 30%, así como un coeficiente de fricción de 0,6 correspondiente a estos mismos niveles de densidad aparente y humedad del suelo obtenido por Ramos et al. (2012).
De la figura se aprecia que los componentes de resistencia frontales (Pp y Pc) son constantes para cualquier valor del ángulo , dependiendo únicamente del grosor de la punta (δ) y del diámetro de la base del cono (a), así como de la tensión de fallo σc.
Asimismo se aprecia que la fuerza de cizallamiento en la parte cilíndrica (Pτ) se incrementa con el aumento del ángulo de la cuña, mientras que la componente de la fuerza de fricción (Pf) en la dirección del movimiento disminuye.
Puede observarse que para ángulos del cono inferiores a 45º, el componente de fricción es superior al de cizallamiento y que para = 30° Pτ es nulo, debido a que desaparece la parte cilíndrica del cono, tomando en este caso una forma geométrica cercana a la normalizada por la ASAE.
Conociendo el valor de la fuerza de penetración, es posible calcular el índice de cono (CI) dividiendo la fuerza total por el área de la base del cono:
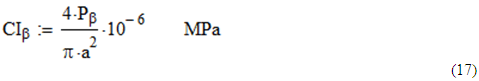
La representación gráfica de esta expresión se muestra en la Figura 4, de la que se aprecia un incremento del valor obtenido en la resistencia a la penetración por unidad de área de la base del cono a medida que se incrementa el ángulo .
Validación del modelo
A manera de validación del modelo propuesto, se efectuó una comparación del resultado calculado, con el obtenido experimentalmente durante una investigación realizada en el mismo tipo de suelo por Laffita (2012), donde fueron tomadas muestras del índice de cono para humedad de 30% y densidad aparente de 1,1, obteniéndose valores medios de 843,84 kPa.
Para estos valores de humedad y densidad aparente, los resultados de ensayos triaxiales de muestras de este propio suelo, obtenidos por Herrera (2006), arrojaron, para una tensión de confinamiento 3= 196 kPa, tensiones de fallo de σ1= 253,8 kPa.
Para un cono normalizado según ASAE (1991), de ángulo α=30º como el empleado por Laffita (2012), la predicción de la resistencia a la penetración (CI) obtenida al evaluar el modelo, arroja un valor de 820 kPa, obteniéndose un error en la predicción de:

CONCLUSIONES
• Partiendo del análisis del equilibrio de fuerzas actuantes durante la penetración de una sonda de punta cónica en el suelo, se obtiene un modelo teórico que permite predecir el comportamiento de los componentes y resultante de las fuerzas que actúan sobre la sonda, así como calcular la resistencia a la penetración, expresada a través del índice de cono.
• La evaluación del modelo para conos de diferente ángulo, manteniendo constantes el área de la base del cono, así como la longitud efectiva de la sonda, arrojó que tanto la fuerza de penetración, como la resistencia a la penetración calculadas, se ven incrementadas con el aumento del ángulo del cono.
• La comparación de la resistencia a la penetración calculada mediante el modelo, evaluado con los datos geométricos correspondientes a un cono normalizado ASAE, con resultados experimentales obtenidos en un suelo Ferralítico Rojo, arrojó un error de predicción de 2,8%.
REFERENCIAS BIBLIOGRÁFICAS
1. ADAMCHUK, V. I.: On-the-go soil sensors for precision agriculture, Computers and Electronics in Agriculture, (44): 71-91, 2004.
2. ALIHAMSYAH, T.; E.G. HUMPHRIES; C.G. BOWERS: A technique for horizontal measurement of soil mechanical impedance, Transactions of the ASABE, 33(1): 73–77, 1990.
3. ANDRADE-SANCHEZ, P.; S.K. UPADHYAYA; B.M. JENKINS & F.A. GARCIAS: "Evaluation of the UC Davis Compaction Profile Sensor", En: ASAE Paper Number 021185, 14pp, 28- 31 July 2002.
4. ANDRADE-SANCHEZ, P.; S.K. UPADHYAYA; C. PLOUFFE; B. POUTRE: Development and field evaluation of a field-ready soil compaction profile sensor for real-time applications, Appl. Eng. Agric., 24(6): 743–750, 2008.
5. ASAE: "Soil cone penetrometer", En: Agricultural Yearbook, ASAE Standards S.313.2. pp. 591, USA, 1991.
6. CHUNG, S. O.; K. A. SUDDUTH: Soil failure models for vertically operating and horizontally operating strength sensors. Transactions of the ASABE, 49(4): 851-863, 2006.
7. CHUNG, S.O.; K.A SUDDUTH; P. P. MOTAVALLI; N. R. KITCHEN: Relating mobile sensor soil strength to penetrometer cone index, Soil & Tillage Research, (129): 9–18, 2013.
8. GLANCEY, J.L., K. UPADAHYAYA; J. CHANCELLOR; W. RUMSEY: An instrumented chisel for the study of soil-tillage dynamics, Soil and Tillage Research, (14): 1–24, 1989.
9. HALL, H. E. & R. L. RAPER: Development and concept evaluation of an on-the-go soil strength measurement system, American Society of Agricultural Engineers, 48(2): 469477, 2005.
10. HEMMAT, A., A.R. BINANDEH; J GHAISARI; A. KHORSANDI: Development and field testing of an integrated sensor for on-the-gomeasurement of soil mechanical resistance, Sensors and Actuators, (198): 61–68, 2013.
11. HERRERA, M: Simulación del comportamiento mecánico de los suelos Ferralíticos rojos mediante el método de elementos finitos, 107pp., Tesis en opción al grado científico de Doctor en Ciencias Técnicas Agropecuarias. Universidad Agraria de La Habana, San José de las Lajas, Mayabeque, Cuba, 2006.
12. HERRERA, M.; C. E. IGLESIAS; D. LARA; O. GONZÁLEZ y E. LÓPEZ: Desarrollo de un sensor para la medición continua de la compactación del suelo, Revista Ciencias Técnicas Agropecuarias, 20(1): 6-11, 2011.
13. HETTIARATCHI, D.R.P. & A.R. REECE: The calculation of passive soil resistance, Geotechnique 24(3): 289–310, 1974.
14. JOHNSON, J.B.: A Statistical Micromechanical Theory of Cone Penetration in Granular Materials, US Army Corps of Engineers Engineer Research and Development Center, (ERDC/CRREL) TR-03-3, USA, 2003.
15. LAFFITA, L. A: Determinación del coeficiente de fricción suelo metal para un suelo Ferralítico rojo lixiviado. Tesis opción al título académico de Máster en Mecanización Agrícola. Universidad Agraria de La Habana. San José de las Lajas, Mayabeque, Cuba, 2012.
16. MOUAZEN, A.; K. DUMONT; K. MAERTENS & H. RAMON: Two- dimencional prediction of spatial variation in topsoil compaction of a sandy loam field based on measured horizontal force of compaction sensor, cutting depth and moisture content., Soil & Tillage Research, 74(1): 91–102, 2003a.
17. MOUAZEN, A. & H. RAMOS: Expanding implementation of an on-line measurement system of topsoil compaction in loamy sand, loam, silt loam and silt soils, Soil &Tillage Research, (103): 98-104, 2009.
18. MOUAZEN, A.; H. RAMOS & D.E. BERDEMAEKER: Modelling compaction from on-line measurement of soil properties and sensor draught. Precision Agriculture, 4(2): 203-212, 2003b.
19. NADERI-BOLDAJI, M.; R. ALIMARDANI; A.HEMMAT; A. SHARIFI; A. KEYHANI; Z. M. TEKESTE & T. KELLER: 3D finite element simulation of a single-tip horizontal penetrometer–soil interaction. Part I: Development of the model and evaluation of the model parameters, Soil & Tillage Research, (134), 153–162. 2013.
20. OWEN, G.T.; H. DRUMMOND; L. COBB & J. GODWIN: An instrumentation system for deep tillage research, Transactions of the ASAE, 30(6): 1578–1582, 1987.
21. RAMOS, C. E., A. LAFFITA, A. GARCÍA DE LA FIGAL, P.A. VALDÉS y R. TORRES: Determinación experimental del coeficiente de fricción dinámico suelo-metal en un suelo ferralítico rojo. Revista Ciencias Técnicas Agropecuaria, 21(3): 35-40, 2012.
22. SCHURING, D. J. & R. I. EMORI: Soil deforming processes and dimensional analysis. SAE Paper No. 897C. New York, USA, 1964.
23. SHEN, J. & R.L. KUSHWAHA: Soil–Machine Interaction, A Finite Element Perspective, New York: Marcel Dekker, Inc., USA, 1998.
24. SHMULEVICH, I.: State of the art modeling of soil–tillage interaction using discrete element method, Soil & Tillage Researc, (111): 41–53, 2010.
25. STAFFORD, J.V.; J.G. HENDRICK: Dynamic sensing of soil pans, Transactions of the ASAE, 31(1): 9–13, 1988.
26. SUDDUTH, K. A.; J. W. HUMMEL and S. J. BIRRELL: "Sensors for site specific management", En: The State of Site-Specific Management for Agriculture: 1997.
27. WISMER, R. D., and H. J. LUTH: "Performance of plane soil cutting blades in clay". Trans. ASAE 15 (2): 211-216. 1972.
Recibido: 22 de diciembre de 2013.
Aprobado: 22 de julio de 2014.
Ernesto Ramos Carbajal. Universidad Agraria de La Habana. Facultad de Ciencias Técnicas. Centro de Mecanización Agropecuaria. San José de las Lajas, Mayabeque, Cuba. Correo electrónico: carbajales@unah.edu.cu