Mi SciELO
Servicios Personalizados
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Revista Ciencias Técnicas Agropecuarias
versión On-line ISSN 2071-0054
Rev Cie Téc Agr vol.26 no.1 San José de las Lajas ene.-mar. 2017
ARTÍCULO ORIGINAL
Modelos matemáticos para la simulación del caudal en vertedores Cipolleti utilizados en sistemas de riego
Mathematical Models for Flow Simulation in Cipoletti Weirs Used in Irrigation Systems
M.Sc. Luis Manuel Sandoval-Mendoza,I Ing. Julio Adrián Miranda-Escobar,I Dr.C. Oscar Brown-Manrique,II Dr.C. Albi Mujica-Cervantes,II Dr.C. Jorge Douglas Bonilla-Rocha,II Dr.C. Yurisbel Gallardo-Ballat,II
IUniversidad de San Carlos de Guatemala (USAC), Facultad de Ingeniería, Guatemala.
IIUniversidad de Ciego de Ávila (UNICA), Facultad de Ciencias Técnicas, Centro de Estudios Hidrotécnicos, Ciego de Ávila, Cuba.
RESUMEN
En este trabajo se presentan los resultados de la investigación desarrollada en el Laboratorio de Mecánica de Fluidos e Hidráulica de la Universidad de San Carlos de Guatemala, donde se construyeron diferentes vertedores Cipolleti con distintos valores de base (b) en el rango de 5 a 60 centímetros. Se encontró un modelo polinomial de segundo orden para la estimación de los parámetros K y n de la ecuación exponencial para la estimación del caudal y una función potencial para el coeficiente de descarga Cd. El modelo para estimar el caudal teórico sugerido por los manuales de hidráulica e hidrometría y el obtenido mediante el programa estadístico SPSS presentaron los mayores errores relativos; sin embargo el resto de los modelos evaluados mostraron una buena correlación con los caudales observados con porcentajes de error menor al 2%. El modelo experimental general que relaciona el coeficiente de descarga obtuvo valores confiables para todos los anchos evaluados y alturas de carga (H) entre 4 y 10 centímetros.
Palabras clave: medición del flujo, calibración, canal hidrodinámico, coeficiente de descarga.
ABSTRACT
This paper presents the results of the research carried out at the Laboratory of Fluid Mechanics and Hydraulics of the University San Carlos de Guatemala, where different weir Cipolleti were built with different values of base (b) in the range of 5-60 centimeters. A polynomial model of second order to estimate the parameters K and n of the exponential equation to estimate the flow and potential for discharge coefficient Cd function was found. The model to estimate the theoretical flow rate suggested by the hydraulics and hydrometrics manual and the one obtained by SPSS statistical program presented the highest relative errors; however, the rest of the tested models showed a good correlation with the observed flow rates of error less than 2%. The general experimental model relating discharge coefficient obtained reliable values for all evaluated widths and load heights (H) between 4 and 10 centimeters.
Key words: calibration, discharge coefficient, hydrodynamic channel, flow measurement.
INTRODUCCIÓN
La agricultura es una actividad económica de alto consumo de recursos hídricos que requiere acciones estratégicas para aumentar la eficiencia en el uso del agua basadas en la tecnificación y modernización del riego superficial (Olvera et al., 2014), que contribuya a la reducción de las pérdidas de agua que se produce por conducción, filtración y percolación.
El diseño eficiente del riego superficial permite suministrar el caudal óptimo1; además su magnitud debe ser conocida, para que el agricultor pueda implementar la medición del caudal (Bello y Pino, 2000; Durán y García, 2007), no solo para el control del agua; sino también para el mejoramiento de su distribución (Instituto para la Diversificación y Ahorro de la Energía, 2005). Esta medición se realiza usualmente con vertedores, que consisten en una pared que intercepta la corriente de un líquido con superficie libre, causando una elevación del nivel aguas arriba de la misma (Sotelo, 2002); sin embargo, la complejidad de los fenómenos hidráulicos en estas estructuras justifica el uso de laboratorios de investigación (Rodríguez et al., 2015) y la modelación matemática para reproducir los cambios de patrones de flujo que ocurren en estos dispositivos (Bacolla et al., 2004). Teniéndo en cuenta los aspectos expresados anteriormente, el objetivo del trabajo consiste en proponer modelos matemáticos que permitan la simulación con exactitud del caudal en vertedores Cipolleti utilizados en sistemas de riego.
MÉTODOS
La investigación se desarrolló en el Laboratorio de Mecánica de Fluidos e Hidráulica de la Universidad de San Carlos de Guatemala que consta de un sistema de abastecimiento de agua por medio de bombeo y un tanque para aforos volumétricos. Para el desarrollo de los experimentos se diseñaron y fabricaron ocho vertedores trapezoidales tipo Cipolleti con una lámina de hierro de 3 mm de espesor y recubierta con pintura anticorrosiva para alargar el tiempo de uso de los vertedores.
Las dimensiones de vertedores se determinaron acorde con las proporciones de los canales de llegada disponibles en el laboratorio. La relación de los taludes se fijó en 1:4 por ser una característica de los vertedores Cipolleti; sin embargo, se varió el valor de la base (b) en el rango de 5 a 60 cm. Los vertedores de 5 a 15 cm de ancho de base fueron colocados dentro del canal hidrodinámico para ensayos de vertedores (canal pequeño) y en el canal contiguo se instalaron los vertedores de 20 a 60 cm de ancho de base como se muestra en la Figura 1.
En cada vertedor se realizó un bisel para que el fluido tenga menor contacto con la pared y su salida sea en forma parabólica, lo que permite el establecimiento de una zona aireada bajo la cresta de la escotadura. Este juega un papel importante, debido a que no permite que el flujo se deslice sobre la cara exterior por lo que disminuye el efecto de la viscosidad sobre la pared del vertedor.
Con el propósito de fijar el vertedor en la salida del canal hidrodinámico y evitar fugas o filtraciones que pudieran afectar las mediciones fue necesaria la colocación de tiras de caucho de 25 mm de ancho en el perímetro de los vertedores con base menores a 15 cm. En el caso de vertedores de ancho grande se colocó sikaflex como adhesivo y sellador.
En los vertedores pequeños (b < 15 cm) los ensayos se realizaron en el canal hidráulico del laboratorio y en los vertedores grandes (b > 20 cm) se utilizó el canal contiguo. En todas las mediciones de altura (H) se controló el caudal suministrado para lograr su estabilización; sólo se consideró como lecturas válidas las que presentaron zona aireada bajo la lámina vertiente.
La distancia (d) para la toma de las lecturas H se calculó teniéndose en cuenta la condición d ≥ 4H; por lo que en vertedores de ancho pequeños la distancia fue de 51 cm y en los vertedores anchos de solera grandes la distancia fue de 100 cm; midiéndose desde la posición del vertedor en sentido longitudinal.
Por cada lectura de carga H realizada se efectuaron tres aforos volumétricos para calcular mediante promedio aritmético el caudal que circula por los vertedores y posteriormente obtener la ecuación experimental de cada uno de ellos mediante la siguiente ecuación:

donde:
Qobs: caudal observado (L/s);
V: volumen captado en el recipiente colector calibrado (L);
T: tiempo para captar el volumen en el recipiente (s).
El caudal experimental se estimó como en la mayoría de medidores de caudal mediante el siguiente modelo de tipo exponencial:
![]()
donde:
Qexp: caudal experimental para cada tipo de vertedor (L/s);
H: altura sobre la cresta del vertedor (cm);
K y n: coeficientes de ajustes.
En el modelo anterior se hizo lineal la relación entre Q y H a partir de la construcción de un gráfico de LogQ = f (LogH); obteniéndose un modelo lineal del tipo Y= aX-b de donde Y = LogQ y X = LogH. De este modose obtuvieron los valores de K y de n de la forma siguiente:
![]()
![]()
El modelo calibrado para la obtención del caudal real en vertedores trapezoidales tipo Cipolleti se determinó como sigue:
![]()
donde:
Qcalib: caudal real obtenido por la calibración de los vertedores (L/s);
Qt: caudal teórico (L/s);
Cd: coeficiente de descarga.
Asimismo, el modelo para obtener el caudal teórico para vertedores trapezoidales es:
![]()
donde:
Qt:caudal teórico (L/s);
b: longitud de la cresta del vertedor (m);
H: altura observada (m).
Sustituyendo la ecuación (6) en la ecuación (5) se obtiene:
![]()
El coeficiente de descarga se obtuvo a partir de la construcción de un gráfico de caudal real contra caudal teórico el cual se ajustó a un modelo lineal; donde la pendiente de la recta es el valor del coeficiente de descarga el cual se utilizó en la generación de un modelo matemático a partir del programa estadístico informático Statistical Package for the Social Sciences (SPSS) con el cual se relacionaron las distintas bases de los vertederos trapezoidales b, la altura de carga H para la simulación del caudal Q que responde al siguiente modelo:
![]()
donde:
Q: caudal obtenido con el modelo (L/s);
b: base del vertedor (cm);
H: altura de la carga observada (cm);
K y n: constantes del modelo a determinar con el programa SPSS.
La ecuación experimental general para la estimación del caudal descargado por el vertedor Cipolleti (Qgen) se obtuvo a partir de deducir una función para calcular el coeficiente de descarga respecto a la base del vertedor que fue sustituida posteriormente en la ecuación (7).
La validación de los modelos propuestos se realizó mediante el error relativo promedio (Erp) el cual permite la comparación entre el caudal observado y el simulado mediante los diferentes procedimientos utilizados en la investigación (Qsim). La ecuación empleada fue la siguiente:
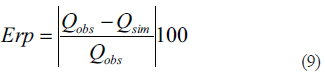
donde:
Erp: error relativo promedio;
Qobs: caudal observado (L/s);
Qsim: caudal simulado (L/s).
RESULTADOS Y DISCUSIÓN
Análisis de los parámetros K y n para el ajuste del modelo exponencial
En la Figura 2 se presentan los resultados alcanzados en condiciones de laboratorio de los parámetros K y n respecto al valor de la base del vertedor. Se comprobó que ambos parámetros se relacionan con la base del vertedor b mediante una función polinomial de segundo orden. En el caso del parámetro n el coeficiente de determinación encontrado fue aceptable con valor de 0,70; sin embargo el parámetro K alcanzó un ajuste excelente con un coeficiente de determinación superior a 0,97. Estos resultados permitieron la construcción del modelo exponencial del tipo Qexp=KHn para la simulación de los caudales experimentales en cada vertedor evaluado.
Análisis del coeficiente de descarga Cd para la calibración de la ecuación del vertedor
En la Figura 3 se muestra el comportamiento del coeficiente de descarga Cd para la calibración de la ecuación del vertedor. Se demostró que la relación funcional de este coeficiente con la base del vertedor es del tipo potencial con un coeficiente de determinación de 0,979. El exponente de esta función tiene pendiente negativa; lo que indica que en la medida en que el valor del ancho de la base se incrementa, se reduce de forma proporcional el coeficiente de descarga. Los valores de este coeficiente encontrado en esta investigación oscilan entre 1,01 y 1,31; sin embargo, otros autores como Arteaga (1993), Roldán et al. (1993) y Pérez (2015), ofrecen coeficientes de descarga entre 0,66 y 0,75 para condiciones similares de altura del agua sobre la cresta, lo que indica que el vertedor Cipolleti evaluado en esta investigación presenta una capacidad superior para la descarga de flujo, lo cual es importante para decidir su utilización en obras hidráulicas en función del caudal que requiera ser desaguado.
Análisis de los modelos para la estimación de los caudales
En la Tabla 1 se exponen los modelos Qexp y Qcalib encontrados para la estimación del caudal en vertedores Cipolleti. En todos los casos se encontró un coeficiente de determinación superior a 0,96 lo que indica un ajuste excelente de los datos experimentales a los modelos evaluados. En el modelo que permite determinar el caudal Qexp se encontró que el coeficiente K varío en el rango 0,07 - 0,99 con una tendencia creciente en la medida en que se incrementó el valor de la base y el exponente n alcanzó valores en el entorno de 1,51-1,75.
En el modelo que permite determinar el caudal Qcalib el exponente se mantuvo fijo con un valor de 3/2; pero el coeficiente se comportó de manera similar al modelo descrito anteriormente con valores comprendidos entre 0,22-1,13.
El modelo para estimar el caudal del vertedor obtenido mediante el programa SPSS (QSPSS) se expone a continuación:

Este modelo presenta un elevado coeficiente de determinación y permite estimar el valor del caudal que descarga un vertedor Cipolleti para cualquier valor de la base b a partir de la medición de la altura del agua sobre la escotadura (H).
En la tabla 1 se comprueba que para la estimación de los caudales Qexp y Qcalib se requiere una función específica para cada ancho de la base; sin embargo este inconveniente fue resuelto mediante la deducción de una ecuación experimental general deducida de la forma siguiente:
![]()
La sustitución de la ecuación (11) en la ecuación (7) resulta la ecuación (12):
![]()
donde:
Qgen: caudal obtenido con la ecuación experimental general (L/s);
b: base del vertedor (cm);
H: altura de la carga observada (cm).
Análisis de la comparación entre los diferentes modelos evaluados en la investigación
En la figura 4 se muestra el resultado de la comparación entre los diferentes modelos evaluados en la investigación. Se constató que las ecuaciones deducidas para estimar el caudal en vertedores Cipolleti fueron muy precisas al lograr resultados similares a los caudales observados; sólo el caudal teórico (Qt) y el caudal obtenido mediante el programa SPSS (IBM Corporation, 2003) (QSPSS) mostraron tendencias a la subestimación y la sobreestimación respectivamente de los valores de esta variable.
Análisis de los errores cometidos por los modelos en la estimación del caudal
Los errores cometidos por los modelos evaluados en la estimación del caudal se analizaron a través del error relativo promedio (Erp). En la Tabla 2 se demuestra que los modelos para determinar los caudales Qexp, Qcalib y Qgen presentan valores inferiores al 2% por lo que pueden ser utilizados de manera confiable en el control de flujos en condiciones abiertas. Los resultados más desfavorables se encontraron en los modelos Qt y QSPSS con un error de 5,49% que resultó ser superior al límite máximo permisible de 5%. Este comportamiento indica que no deben aplicarse para determinar el caudal en vertedores Cipolleti.
Los resultados alcanzados en esta investigación están asociados al riguroso trabajo de diseño y construcción de los vertedores evaluados; así como a la obtención de los datos experimentales. En este sentido Aguilar (2001), se refirió a la necesidad de verificar de forma correcta diferentes parámetros como altura y ancho del vertedor Cipolleti; pues de no cumplirse la precisión en la estimación del gasto, no es confiable. En este mismo sentido Bos et al. (1986) y Santos et al. (2010), afirmaron que es necesario lograr un adecuado diseño e instalación del aforador para medir y regular el caudal de agua de los canales de riego; puesto que el correcto diseño y empleo de estas instalaciones puede contribuir a disminuir la sobreexplotación de acuíferos y al ahorro energético por menores necesidades de bombeo (Instituto para la Diversificación y Ahorro de la Energía, 2005).
Este trabajo pueden contribuir al ahorro de los recursos hídricos a través del perfeccionamiento de la medición de los caudales mediante vertedores Cipolleti; pues según García y Pérez (2004) y Tarjuelo (2005), es necesario la utilización eficiente y el manejo eficaz de estos dispositivos ya que el agua es un recurso cada vez más escaso y existe más competencia entre sus diversos usos; por tanto, las estrategias para lograr la sustentabilidad de los sistemas de riego debe tener en cuenta la instalación de sistemas de medición, que permitan el control de la cantidad de agua empleado por el usuario Fernández et al. (2009).
CONLUSIONES
-Los modelos para la estimación de los caudales Qexp, Qcalib y Qgen presentaron una buena correlación con los caudales observados, lo que permite obtener errores menores al 2%.
-La ecuación experimental general que relaciona las alturas de carga, base y coeficiente de descarga obtuvo valores confiables para vertederos con ancho menor a 60 cm y alturas de carga (H) entre 4 y 10 centímetros.
-Los coeficientes de ajuste del modelo exponencial Q = KHn mostraron una aceptable relación funcional con el ancho de la base del vertedor Cipolleti; lo que permitió encontrar un modelo polinomial de segundo orden para la estimación de forma confiable de los parámetros K y n.
-Los coeficientes de descarga Cd no fueron constantes y su valor tiende a disminuir al aumentarse la base como lo demuestra el modelo matemático de tipo potencial con pendiente negativa.
-El modelo sugerido por los manuales de hidráulica e hidrometría para la estimación del caudal teórico en los vertederos Cipolleti presentó errores superiores al 5%.
NOTAS
*La mención de marcas comerciales de equipos, instrumentos o materiales específicos obedece a propósitos de identificación, no existiendo ningún compromiso promocional con relación a los mismos, ni por los autores ni por el editor.
BIBLIOGRAFÍA
AGUILAR, C.A.: Vertedores, [en línea], Rivas, A.I. (ed.), ser. Autodidáctica de Medición, Ed. Comisión Nacional del Agua - Instituto Mexicano de Tecnología del Agua, México D.F., 23 p., 2001, ISBN: 968-5536-02-3, Disponible en: http://repositorio.imta.mx:8080/cenca-repositorio/bitstream/123456789/1115/1/IMTA_097.pdf, [Consulta: 5 de enero de 2017].
ARTEAGA, T.R.E.: Hidráulica elemental, Ed. UAC. Dirección de Difusión Cultural, Departamento de Irrigación, 1.a ed., Chapingo, México, 335 p., 1993, ISBN: 978-968-884-238-6.
BACOLLA, C.; DABIN, A.; FRANCK, G.: “Simulación Numérica de Tomas de Agua en Muelles”, Mecánica Computacional, 23: 2009–2030, 2004, ISSN: 1666-6070.
BELLO, M.A.; PINO, M.T.: “Medición de presión y caudal”, Boletín INIA, 28.a ed., p. 20, Punta Arenas, Chile, 2000, ISSN: 0717-4829.
BOS, M.G.; REPLOGLE, J.A.; CLEMMENS, A.J.: Aforadores de caudal para canales abiertos, Ed. International Institute for Land Reclamation and Improvement, Wageningen, 293 p., 1986, ISBN: 978-90-70260-92-7.
DURÁN, P.J.; GARCÍA, P.M.: “Desarrollo de tecnologías apropiadas para riego por surcos en terrazas paralelas y tierras con pendiente”, Ingeniería del agua, 14(3): 187-198, 2007, ISSN: 1886-4996, 1134-2196, DOI: 10.4995/ia.2007.2911.
FERNÁNDEZ, C.A.; HOLZAPFEL, E.; DEL CALLEJO, I.; BILLIB, M.: Manejo sostenible del agua para riego en sudamérica, Ed. Universidad de Buenos Aires. Facultad de Ciencias Veterinarias, Buenos Aires, Argentina, 175 p., 2009, ISBN: 978-987-25074-1-1.
GARCÍA, G.S.; PÉREZ, L.J.R.: “Resultados de la introducción del riego por goteo en la cooperativa de producción agropecuaria cañera «Primer Soviet de América»”, Revista Ciencias Técnicas Agropecuarias, 13(1): 47-51, 2004, ISSN: 1010-2760.
IBM CORPORATION: IBM SPSS Statistics, [en línea], (Versión 11.5), [Windows], Ed. IBM Corporation, U.S, 2003, Disponible en: http://www.ibm.com.
INSTITUTO PARA LA DIVERSIFICACIÓN Y AHORRO DE LA ENERGÍA: Ahorro y eficiencia energética en agricultura de regadío, Ed. IDAE, Madrid, España, 36 p., 2005, ISBN: 978-84-86850-94-4.
OLVERA, S.M.D.; BAHENA, D.G.; ALPUCHE, G.O.; GARCÍA, M.F.: “La tecnificación del riego ante la escasez del agua para la generación de alimentos. Estudio de caso en Chihuahua, México”, Ambiente y Desarrollo, 18(35): 23-36, 2014, ISSN: 0121-760.
PÉREZ, F.W.J.: “Uso del suelo como tratamiento secundario para la remoción de materia orgánica de las aguas residuales domesticas”, Agua, saneamiento & Ambiente, 10(1): 31-38, 2015, ISSN: 2222-2499.
RODRÍGUEZ, S.J.; VALERO, C.; MENDOZA, K.: “Análisis experimental de coeficientes de descarga en vertederos trapezoidales de pared delgada – Parte I”, Yachana, 4(2): 30-37, 2015, ISSN: 1390-777.
ROLDÁN, J.; PULIDO, I.; CAMACHO, E.; ALCAIDE, M.; LOSADA, A.: Problemas de hidráulica para riegos, Ed. Servicios de publicaciones, Universidad de Córdoba, España, 335 p., 1993, ISBN: 84-7801-526-4.
SANTOS, P.L.; DE JUAN, J.A.; PICORNELL, B.M.R.; TARJUELO, J.M.: El riego y sus tecnologías, [en línea], Ed. CREA-UCLM, 1.a ed., España, 296 p., 2010, ISBN: 978-84-692-9979-1, Disponible en: http://www.academia.edu/download/33889207/El_Riego_y_sus_Tecnologias.pdf, [Consulta: 26 de noviembre de 2016].
SOTELO, Á.G.: Hidráulica general, Ed. Limusa, México, 2002, ISBN: 978-968-18-0503-6.
TARJUELO, J.M.: El riego por aspersión y su tecnología, Ed. Mundi-Prensa, 3.a ed., Madrid, España, 581 p., 2005, ISBN: 84-8476-225-4.
Recibido: 13/01/2016
Aprobado: 14/11/2016
Luis Manuel Sandoval-Mendoza, Prof., Universidad de San Carlos de Guatemala (USAC), Facultad de Ingeniería, Guatemala. Email: ingluissandoval@gmail.com














