INTRODUCTION
The International Trade Center, according Arvelo et al. (2017), referred that, in the period from 2005 to 2017, world trade in fruit practically doubled. This factor, combined with the export capacity in the Americas, opened up new opportunities for the regional merchant sector in developing countries and emerging markets.
Fruits of excellent development in the tropical region such as guavaare recognized for being rich in vitamin C and having wide acceptance in national and international markets. However, it is a fruit highly susceptible to damage. In Cuba, despite having large productions of more than 160 733 t, as reported by the Oficina Nacional de Estadísticas e Información (ONEI, 2017), its location in foreign markets and tourism is negligible. This is due to the fact that there is no norm for the fresh consumption of this fruit, subtracting value, regardless of the fact that guava is a climacteric fruit of wide national consumption and very versatile when consuming as a fresh or processed product (Martínez, 2003).
Fresh guava has a shelf life of 5 to 7 days at room temperature and three weeks at 8 °C (Mercado et al., 1998; Yirat, 2009; Yirat et al., 2009). Based on the Mexican norm NMX-FF-040-2002 (2002), the good quality of guava for human consumption implies, in general, good appearance with slight defects, such as scrapes, scratches, crusts, spots or sunburn, which do not affect their conservation and allow compliancing with the selection parameters. However, the fruit is subjected to a large number of events that cause mechanical damage to the skin, which generate significant economic repercussions and, at times, are difficult to detect at a glance. Some studies show that the loss of product due to mechanical damage is 12% of the total production (Wills et al., 1989; Kader, 2002).
Mechanical damage can detract from the appearance of the product and create the potential for the penetration of infections, they also influence quality and prices (Martínez, 2003). To carry out a study of these damages, the nature of the distribution chain, from production to the consumermust be known, and the elements that are part of it should be defeined. The solicitations to which a fruit is subjected and that generate damage due to the magnitude of the forcesapplied, can be classified, basically, in three types: compression, impact and vibration (Berardinelli et al., 2005; Lewis et al., 2007, 2008).
In recent years, as a result of the improvement of electronics and computing, considerable progress has been made in the development of non-destructive technologies for predicting and monitoring the emergence of mechanical damage in agricultural products(Ciro&Osório, 2008). Other examples of them are the reports of Baettig (2001) and Valente &Ferrandis (2003) by using acoustic methods, Santonicoet al. (2010) and Jhaet al. (2012) by means ofelectronic nose andGejimaet al. (2003) and López & Gómez (2004) by utilizing methods of image processing, among others. Inthe 21st century, mathematical or numerical methods have been deepened to this end, including artificial neural networks and the finite element method (FEM), which have been used in order to know or predict the efforts generated and establish the loading thresholds that the tissue experiences before these events (Lewis et al., 2007, 2008; Sadrnia et al., 2008). The present work of investigation proposes like objective: tosimulate the mechanical behavior of guava fruit, variety Red Dwarf EEA 1-23, under the action of loads of impact, usingFEM as way for the prediction and possible reduction of mechanical damages.
MATERIALS AND METHODS
Experimental Conditions and Sampling
The samples of the fruits under study were obtained in "Las Papas" Farm belonging to the National Institute of Agricultural Sciences located in Mayabeque Province, Cuba. The plants were 7 years old and had a planting frame of 2 m x 2 m. For the collection of samples, a panel of experts was used, using the fruit size as a common criterion, classifying according to two maturation stages (MS-I: green-made and MS-III-mature) (Table 1), according toYirat (2009) and Yirat et al.(2009).
Only two maturation stages are selected because the fruit is usually harvested for export in the MS-I state (physiological maturity) and is usually more susceptible to damage in the MS-III (mature) state, hence the most interesting ones.
The number of samples is determined through Expression 1, using the statistical program STATGRAPHICS Plus 5.1.
Impact Tests
The sampled fruits were transported at room temperature for processing to the quality laboratory of the Agrarian University of Havana, in a time not exceeding 5 min. At the time of receiving, all fruits were listed and weighed. Once subjected to the impact tests, their behavior was controlled until 64 h after the damage arose. Two levels of impact were caused by freely dropping fruits from two heights: 0.5 m and 1.0 m, on two types of surface: wood and concrete, as they correspond to the characteristics of the post-harvest guava processes in Cuba.
To carry out this test the samples were divided into five groups of 10 fruits each, for 100 samples, of which 20 were not subjected to impact, remaining ascontrol. Table 2 shows the experimental design of the impact tests.
TABLE 2 Fruit groups analyzed in the experiment
| Group | Amount of fruits | Maturationstates | Fallheights | Fallingsurface |
|---|---|---|---|---|
| 1 | 10 | 1 m | Concrete (C-1 m) | |
| 2 | 10 | 0,5 m | Concrete (C-0,5 m) | |
| 3 | 10 | 1 m | Wood (W-1 m) | |
| 4 | 10 | 0,5 m | Wood (W -0,5 m) | |
| 5 | 10 | |||
| 1 | 10 |
|
1 m | Concrete (C-1 m) |
| 2 | 10 | 0,5 m | Concrete (C-0,5 m) | |
| 3 | 10 | 1 m | Wood (W-1 m) | |
| 4 | 10 | 0,5 m | Wood (W-0,5 m) | |
| 5 | 10 |
The monitoring was carried out at 0, 24, 48 and 64 hours after the experiments, since, according to Falcón et al. (2011), the fruits of this variety subjected to impact begin to show the effect of the damage 24 hours after the impact. During the monitoring, the main properties that define the conservation and quality of the fruit were taken into account, as well as the appearance of the damage. The conservation was carried out at room temperature in wooden packaging, controlling the climatic variables of local and external temperature, as well as the relative humidity.
Determination of Physical-Mechanical Properties
The main physical-mechanical properties required in the research process were determined experimentally. The methods and means used in the different determinations are described below:
Size: The polar diameter (m) and the equatorial diameter (n) were measured with a STAINLESS HARDENED digital vernier, (Annex 5, Figure 4) from 0 to 150 mm ± 0.01 mm precision. Averagevalues weredetermined andother relevant statisticians, as well as for the rest of the properties object of determination.
Mass: It was determined using an electronic balance model LG-1001ª from 0 to 1000 (g) / 0.1 (g) of Chinese manufacture. Three repetitions per fruit were made.
Density: It was determined applying Archimedes Principle from obtaining the mass and the volume displaced during the immersion of the fruit in a container with water, according to Expression 2 (Martínez et al., 2017).
Elastic Limit: Young'sModulus,the apparent Poisson's coefficient of guava fruit and the maximum breaking stress were determined with the use of a digital compactometer model CEMA-C08, based on the MagnessTaylor Principle, 0 to 1000 (kgf) / 0.01 (kgf), manufactured domestically.
The elasticity limit of guava fruits was determined usingthe method proposed by Chávez et al.(2000) and utilizing Expression 3 to determine the effort.
The Young's Modulus or apparent elasticity moduluswas determined from Expression 4 (Mercado et al., 2005).
where:
E |
- Modulus of elasticity, (MPa); |
Fm |
- Maximum firmness to compression before breaking the fruit, (N); |
L |
- Longitudinal diameter, (mm); |
ΔL |
- Deformation of the longitudinal diameter, (mm). |
Apparent Poisson Coefficient: It was determined from Expression 5 (Ciro&Osório, 2008 and Shirmohammadiet al., 2012), based on the definition of Poisson's Coefficient:
Damage Assessment by Impact
Visual damage was measured using the methodology proposed by Menesatti & Paglia (2001),with the help of a caliper from 0 to 150 mm± 0.01 mm precision STAINLESS HARDENED mark. Measurements were taken on two perpendicular axes (smaller diameter and larger diameter, Figure 1) of the damaged area (usually elliptical), and, with this, the area A of the bruise was calculated by Expression 6.
where:
Dd |
- maximum dimension of the damaged area, (m); |
Sd |
- minimum dimension of the damaged area, (m). |
To determine the depth of the bruise on the damaged fruit, the methodology proposed by Menesatti & Paglia (2001) was applied. The center of the bruisewas determined and so, the point furthest towards the interior of the fruit and the distance from this point to the outside of the fruit, as shown in Figure 2.
Digitized Model of the Fruit
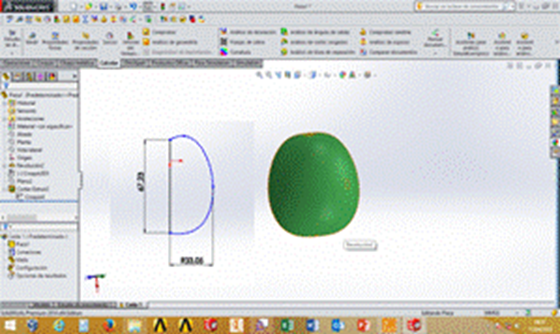
The digitized model of the fruit was made with the help of the SolidWorks 2013 program Shih (2013), with the aim of predicting, by simulation using the finite element method, the behavior of the fruit of the variety Red Dwarf guava EEA 1-23, before impact loads.
For the construction of the geometric model, a volume of revolution was elaborated starting from a transverse half-section of the fruit with maximum diameter and average height. (Figure 3). For the fruit material, a homogeneous-continuous-isotropic-linear-elastic constitutive model wasaccepted.
Once the solid was createdwith the characteristics of the fruit, such as size, shape and appearance, the program was fed with the physical-mechanical properties necessary for this study and which characterize both, the fruit and the materials on which it impacted: density, modulus of elasticity, elastic limit and Poisson's Coefficient. The properties corresponding to wood and concrete were taken from the materials library of SolidWorks 2013 Shih (2013), while for guava, the results of the properties obtained experimentally in the framework of this research were introduced.
After defining the characteristics of the material, the equatorial region of the fruit was chosen as the impact zone and two levels of fall distance were simulated: 1 m and 0.5 m. The initial trace in the impact zone was determined from the deformation that occurs in the fruit by its own weight, supported on the corresponding surface, for which Expression 7, according Pisarenko and Yakovlev (1979), was used, which makes possible todetermine the contact trace between a spherical body and a plane.
where:
P |
- force that intervenes in the fall of the fruit (force of gravity), (N) |
R |
- radius of the fruit, (m) |
μ1 |
- apparent Poisson's coefficient of the fruit |
μ2 |
-apparent Poisson's coefficient of the material impacted by the fruit |
E1 |
- module of apparent elasticity of the fruit, (MPa) |
E2 |
- modulus of elasticityof the impacted material, (MPa) |
Once the geometric model and the properties of the materials were defined, the finite element meshing was carried out using the corresponding SolidWorks 2013 tools Shih (2013).
Prediction of Errors with Respect to the Experimental Model
This procedure was carried out to determine the forecast errors of the model, for which Expression 8 was used (Garcíaet al., 2008).
The measurements obtained from the expression made possible to determine how far the model was able to predict accurately,the value of a variable at a given point. To know the accuracy of the response throughthe model in the evaluated interval, a comparison of samples was made, where the experimental and model values were evaluated, determining the dependence of the results.
RESULTS AND DISCUSSION
Mechanical Physical Properties
Table 4 shows the physical properties that characterize the Red Dwarf hybrid EEA1-23, in the two maturation stages studied. The variability in physical properties depends on several factors, among them, the variety, the conditions of the production environment, the agronomic and nutritional management of the crop, etc. The values of size, mass and density obtained coincide with the ranges definedby Yirat (2009)for this variety.
TABLE 4 Physical properties of the fruit for two stages of maturation
| Properties | Middlevalue | Standard deviation | ||
|---|---|---|---|---|
| MS- I | MS-III | MS-I | MS-III | |
| Polar diameter (m) | 66, 9x10-3 | 67,01x10-3 | 2,07x10-3 | 1,8x10 |
| Equatorialdiameter (m) | 65,9x10-3 | 66,39x10-3 | 2,55x10-3 | 2,15x10-3 |
| Mass (g) | 204,79 | 215,20 | 29,35 | 33,51 |
| Density (g / m3) | 983,06 | 1 008,06 | 34,40 | 26,64 |
Table 5 shows the average results obtained for the elastic limit, the apparent modulus of elasticity and the apparent Poisson's coefficient, which characterize the mechanical properties of the material. The results show that as the fruits reach the stage of maturation III, there is a decrease in the modulus of elasticity due to the resistance of the material with maturation decreases, being more easily deformable by minor efforts. That coincides with Mercado et al. (2005) and Martínez et al. (2017), who state that there is a relationship: lower modulus of elasticity-greater degree of maturity.
TABLE 5 Physical-mechanical properties of guava fruits
| Maturation states | Elasticitylimit (MPa) | Elasticity module (MPa) | Poisson'scoefficient |
|---|---|---|---|
| 0,34 (± 0,018) | 3,71 (± 0, 15) | 0,34 (± 0,026) | |
|
|
0,04 (± 0,004) | 0,51 (± 0,032) | 0,49 (± 0,023) |
Table 6 shows the average values of the area and depth of the bruises of the fruits as a function of the height and the area impacted for each state of maturation. In the fruits of the MS-I, the greatest and depthestareas of bruises were observed in those that were impacted at a height of 1 m in wood and concrete, reporting values of 8.3x10-4 and 25.2x10-4 m2 and 13.6x10-3 and 20.7x10-3 m, respectively. Something similar occurs in the fruits of the MS-III, in which the highest values of the damaged area were observed for impacts from a height of 1 m on concrete and wood surfaces, reaching the areas of bruising average values of 38.04×10-4 and 28.04 x10-4 m2, as well as a depth of 30.4x10-3 and 28.7x10-3 m, respectively. It was appreciated, as expected, that the bruised area induced in the fruit impacted on concrete was superior to the case of wood. This is understandable due to the resistive behavior of both materials, that is, different responses to tensile-compression, modulus of elasticity, deformation, etc. According to O’Brien & Gaffney (1983), the magnitude of the impact damage in fruits depends to a great extent on the physical characteristics of the fall surface.
TABLE 6 Results of the average values of the area and depth of the bruises as a function of the height and the surface impacted by maturation state
| MaturationState | I | |||
| Surfaces | Wood | Concrete | ||
| Height (m) | 0,5 | 1 | 0,5 | 1 |
| Area of bruise (m2) | 4,7x10-4 | 8,3x10-4 | 5,9x10-4 | 25,2x10-4 |
| Depth of the bruise (m) | 9,7x10-3 | 13,6x10-3 | 10,6 x10-3 | 20,7x10-3 |
| State of maturation | III | |||
| Surfaces | Wood | Concrete | ||
| Height (m) | 0,5 | 1 | 0,5 | 1 |
| Bruisearea (m2) | 17,03x10-4 | 28,04x10-4 | 23,6x10-4 | 38,04x10-4 |
| Depth of the bruise (m) | 20,7 x10-3 | 28,7 x10-3 | 21,7 x10-3 | 30,4 x10-3 |
Digital Model to Explain the Behavior of Guava Fruit
Once the solid wasdrawn with the characteristics of the fruit such as size, shape and appearance, the program was fed with the physical and mechanical properties that characterize it as: Modulus of Elasticity, Limit of elasticity, Poisson and Density and meshing was generated obtaining tetrahedral second order solids (Figure 4). An amount of 13 168 elements was obtained with 8 788 nodes. The choice of this element was justified by its high precision and good representativeness of the shape limit according to Martínez et al. (2017), for fruits of elliptical geometry such as guava.
Figure 4 shows a sketch of the fruit highlighting the impact zone (A) and the meshing (B).
Figures 5 and 6 show the equivalent voltages (Von Mises) that occur in the nodes corresponding to the impact zone for different fruit drop heights by ripening states, obtained during the simulation. In Figure 5, the maximum values of stresses or equivalent stresses (Von Mises) produced in fruits in MS-I (indicated in red color), with a fall height of 1 and 0.5 m in both surfaces studiedare shown. They were, for wood, values of 320.9 and 235.7 kPa and for concrete, of 331.8 and 239.7 kPa, respectively. It was evident that these stress values didnot exceed the experimentally determined elastic limit values (340 kPa) for the simulation of the fruit in this state.
In Figure 6, it can be seen that the maximum values of effort for fruits in MS-III, reached 201.5 and 214.2 kPa for those impacted with a fall height of 1 m and 150.5 and 170.2 kPa to 0.5 m, on wood and concrete surface, respectively. It can be stated that for the two stages of maturation studied as the height of fall decreases, the efforts in the nodes of the impact zone also decrease. For the MS-III, at a fall height of 0.5 and 1.0 m, with respect to the impact surface, stresses werecaused that wereabove the value of the stress corresponding to the elastic limit of the fruit tissue. This means that there is a very high probability that the cells of guava fruit tissue have undergone irreversible structural damage and, consequently, changes in their overall metabolism. The tissue of the fruits that receives a mechanical effort, either by static or dynamic load, can have permanent structural damage depending on the intensity of the effort. The immediate effect is the oxidation of phenolic compounds by the enzyme catechol oxidase, which demands an increase in oxygen consumption (Kader, 2002; Knee, 2002; Knee & Miller, 2002; Berardinelli et al., 2005). In guava fruits in MS-I, (Criolla variety) Martínez et al. (2017), reported maximum stress values of 351.2 kPa at a falling height of 1 m and 256.1 kPa at 0.5 m.
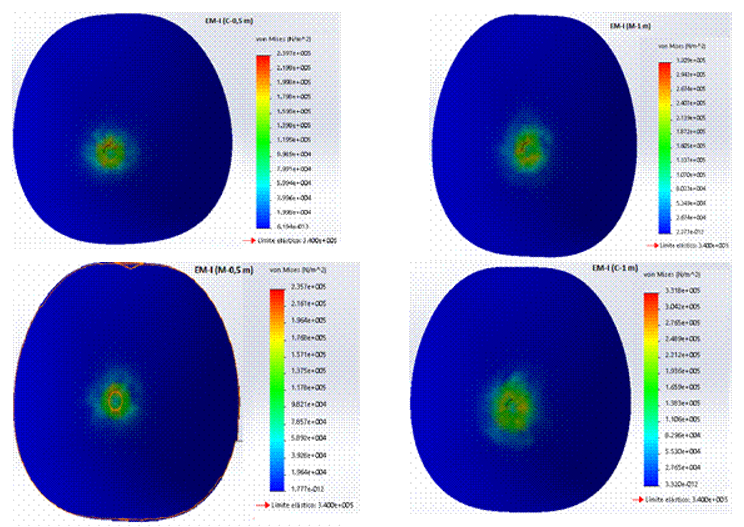
FIGURE 5 Impact effort in the nodes corresponding to the impact zone in the different fruit drop heights at MS-I, during the simulation.
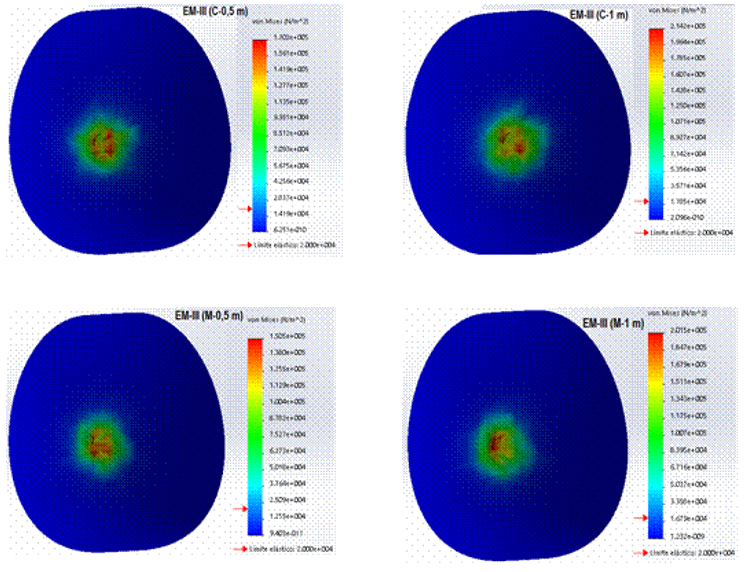
FIGURE 6 Impact effort in the nodes corresponding to the impact zone in the different fruit drop heights atMS-III, during the simulation.
Once simulated the fall of guava fruits in the different heights, surfaces and ripening states analyzed, using the FEM, the dimensions of the area of the bruises obtained in the simulation of these were determinedby Expression 2. Table 8 shows the major (Dd) and minor (Sd) diameters of the bruises, as well as the result of those areas.
TABLE 8 Diameters greater (r), minor (s) and area of the bruises obtained from the simulation of the fruits by FEM
| MaturationState | I | |||
| Surfaces | Wood | Concrete | ||
| Height (m) | 0.5 | 1 | 0.5 | 1 |
| r (m) | 13.5x10-3 | 18.6x10-3 | 14.7x10-3 | 27.6x10-3 |
| s (m) | 11x10-3 | 13.7x10-3 | 12.4x10-3 | 24.9x10-3 |
| Bruisearea (m2) | 4.7x10-4 | 8.04x10-4 | 5.7x10-4 | 21.6x10-4 |
| MaturationState | III | |||
| Surfaces | Wood | Concrete | ||
| Height (m) | 0.5 | 1 | 0.5 | 1 |
| r (m) | 17.7x10-3 | 26.14x10-3 | 25.61x10-3 | 31.82x10-3 |
| s (m) | 15.8x10-3 | 25.77x10-3 | 23.86x10-3 | 27.51x10-3 |
| Bruisearea (m2) | 12.9x10-4 | 20.8x10-4 | 19.2x10-4 | 27.5x10-4 |
Accuracy in the Application of the Digital Model
In order to validate the model, it was necessary to determine the prediction errors in each variable analyzed. Table 9 shows the comparison of the values obtained experimentally with those derived from the evaluation of the digital model throughFEM. It is observed that for the state of maturation I, a precision of the model between 85% and 98% was obtained, whereas for the state of maturity III the precision diminished, it oscillated between 72% and 81%. This behavior indicates that the stress-strain relationship of the mature fruit was further away from the elastic behavior, which is what is accepted in the constitutive model of the material. Despite this result, it can be concluded that, although the process of deformation of the fruit during the impact involves plastic changes and therefore permanent, an elastic model can be considered valid to analyze the behavior of the guava in order to prevent mechanical damage of this type.
TABLE 9 Estimation of the percentage of model errors for deformation
| MS-I | Prediction error (%) | Accuracy of themodel (%) |
|---|---|---|
| W-0,5 m | 1,73 | 98,27 |
| W-1 m | 3,00 | 97,00 |
| C-0,5 m | 1,98 | 98,02 |
| C-1 m | 14,27 | 85,73 |
| MS -III | ||
| W-0,5 m | 24,39 | 75,61 |
| W-1 m | 25,51 | 74,49 |
| C-0,5 m | 18,68 | 81,32 |
| C-1 m | 27,70 | 72,30 |
CONCLUSIONS
The greatest and depthest areas of the bruises were observed in the fruits of the MS-III that were impacted at a height of 1 m in wood and concrete with values of 28.04×10-4 m2 and 38.04×10-4 m2 and 28, 7x10-3 m and 30.4x10-3 m, respectively.
The simulation tests with the FEM showed that, for fruits in MS-III at a fall height of 0.5 and 1 m on the two surfaces studied, the effort reached by the tissue in the impact area was above the value of the elastic limit of the fruit tissue (40 kPa). This suggests that in the post-harvest handling operations the tissue of the impact area begins to experience irreversible damage from these impact heights.
The potential of the FEMwas validated for the simulation of damages in impacted guava on concrete and on wood with a precision of 85 to 98% for fruits in green-ripened state and 72 to 81% for ripe fruits.
For mature fruits, the prediction error was higher than for the green-ripe ripening state, because the behavior of the mature fruit deformation was further away from the elastic behavior, which is what is acceptedas a constitutive model of the fruit.











 texto en
texto en