Mi SciELO
Servicios Personalizados
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Revista Ciencias Técnicas Agropecuarias
versión On-line ISSN 2071-0054
Rev Cie Téc Agr vol.28 no.4 San José de las Lajas oct.-dic. 2019 Epub 01-Dic-2019
ARTÍCULO ORIGINAL
Evaluación de métodos para el cálculo de coeficientes de cargas dinámicas
IUniversidad Autónoma Chapingo (UACh), Departamento de Ingeniería Mecánica Agrícola (DIMA), Texcoco, Chapingo, Estado de México, México.
IIUniversidad Agraria de La Habana (UNAH), Centro de Mecanización Agropecuaria (CEMA), San José de las Lajas, Mayabeque, Cuba.
En las máquinas agrícolas, por lo general actúan fuerzas dinámicas, en particular cargas de impacto, lo que provoca roturas o fallas frecuentes. Esto se debe al carácter impulsivo de estos tipos de cargas, las cuales presentan corta duración en el tiempo, disminuyendo la capacidad de las estructuras y piezas para absorber la energía de deformación. Los métodos de cálculo que permiten obtener los coeficientes de cargas dinámicas, requieren operaciones complejas. En la presente investigación se evalúan y comparan tres metodologías para la obtención de coeficientes de cargas dinámicas: el método analítico tradicional, la simulación numérica basada en el análisis por elementos finitos y el método experimental. Tomando los resultados obtenidos experimentalmente como base comparativa, se obtuvo que los coeficientes de cargas dinámicas obtenidos por el método analítico alcanzaron diferencias relativas al método experimental del orden de 21.82 y 27.20 %, mientras que los resultados obtenidos empleando el método de los elementos finitos alcanzaron una diferencia relativa mucho menor, la cual osciló entre 3.48 y 5.11%, demostrando este método una alta aproximación a la determinación experimental.
Palabras-clave: Elementos finitos; esfuerzos dinámicos; Cargas de impacto; condiciones de frontera
INTRODUCCIÓN
Poder contar con cálculos precisos ycientíficamente justificados de coeficientes de cargas dinámicas garantiza diseños eficientes y un ahorro considerable de materiales en la fabricación de prototipos.
La determinación de los esfuerzos originados por las cargas dinámicas resulta compleja, dependiendo de factores tales como la zona de contacto en el impacto y el proceso de variación, en función del tiempo, de las fuerzas de contacto. En este sentido, la mayoría de los casos dinámicos se tratan de cuantificar en forma experimental y para que los cálculos resulten sencillos se utilizan cargas estáticas equivalentes. La determinación de los coeficientes de cargas dinámicas en estructuras sometidas a acciones de impacto, empleando métodos analíticos, representan un reto por su alta complejidad.
El método de los elementos finitos, como método numérico de discretización asistido por computadora, constituye una vía alternativa al método analítico de análisis del medio continuo, que facilita la solución de problemas complejos de ingeniería, siendo considerado una herramienta de indudable valor práctico y de gran aplicación a nivel mundial. Existen resultados importantes derivados del empleo de este método, entre los cuales se encuentran: Martínez et al.(2007); Liu et al.(2013); Untaroiu et al.(2013); Vavalle et al.(2013); Feng y Aymerich(2014); Nadal et al.(2014); Zhanbiao et al.(2014); Singh y Singh(2015); Zhao et al.(2015); Kong et al.(2016); Xiaofei et al.(2016); Castro y Güiza(2017).
El presente trabajo tiene como objetivo evaluar y comparar tres metodologías de determinación de coeficientes de cargas dinámicas: el método analítico tradicional (MA), la simulación numérica basada en el análisis por elementos finitos (MEF) y el método experimental (Mexp), tomándose este último como patrón de comparación y validación de los métodos teóricos.
MÉTODOS
Se empleó un diseño tipo multifactorial, utilizando 2 factores como variables independientes que corresponden a la altura y la carga de impacto, con diez y tres niveles, respectivamente. Los niveles de cargas fueron 25; 400 y 800 N y para laaltura de impacto desde 0 hasta 1 m con intervalos de 0.1 m.
Para los tres métodos analizados, el coeficiente de cargas dinámicas se determinó partiendo de la determinación de la deflexión estática producida sobre un sistema mecánico tomado como objeto de estudio bajo la acción de cargas estáticas con una magnitud igual al peso de un cuerpo que impacta a una determinada altura. Una vez determinadas las deflexiones estáticas máximas del sistema objeto de estudio, el coeficiente de cargas dinámicas se determinó empleando la expresión segúnPisarenko y Yakovlev (1979):
donde:
kd |
- Coeficiente de cargas dinámicas ; |
δest |
- deflexión o flecha estática máxima, que depende también del esquema de solicitación y las condiciones de apoyo; |
H |
- altura de caída del cuerpo que impacta sobre el sistema objeto de estudio. |
En este trabajo, la deflexión estática del sistema objeto de estudio fue determinada por los tres métodos mencionados: el método analítico tradicional de la mecánica de materiales; el método de los elementos finitos y el método experimental.
Descripción del sistema mecánico objeto de estudio
Como objeto de estudio se empleó una viga de sección transversal cuadrada(Tabla 1) en posición horizontal y apoyada en sus extremos con una articulación y un simple apoyo, como se muestra en la Figura 1.En el centro de la viga se aplicaban tres niveles de cargaQ (25, 400y 800 N) con vistas a provocar diferentes niveles de deflexiones estáticas(δ).En la Tabla 2 se muestran las propiedades mecánicas del material.
TABLA 1 Descripción del sistema en estudio
| Sección transversal | Lado, mm | Masa, kg | Momento de inercia, m4 | Longitud, mm | Carga que actúa, N |
|---|---|---|---|---|---|
| cuadrada | 39.09 | 12 | 1.95*10-7 | 1000 | De 25 a 800 a intervalo de 25 |
TABLA 2 Propiedades físico mecánicas del material de la viga
| Descripción | Valor |
|---|---|
| Módulo de elasticidad | 200 000 MPa |
| Coeficiente de poisson | 0.29 |
| Densidad de masa | 7900 kgm-3 |
| Limite a tracción | 420.507 MPa |
| Limite elástico | 351.561 MPa |
Fuente: Warrendale(2001)
Determinación de las deflexiones estáticas por el método analítico tradicional
Para el caso objeto de estudio, consistente en una viga horizontal simplemente apoyada y cuando la aplicación de la carga se efectúa en el centro de la viga, la flecha estática máxima está dada por la expresión:
Aplicación del Método de los Elementos Finitos (MEF)
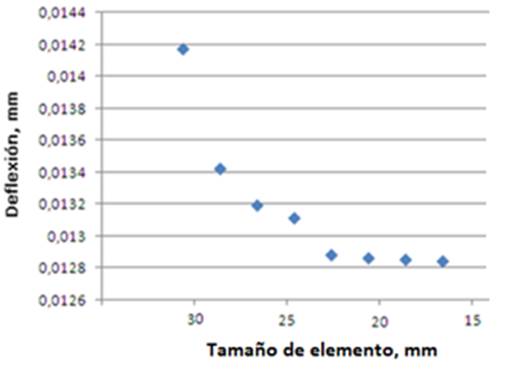
La calidad del análisis por elementos finitos se garantizó efectuando un estudio de convergencia para definir el tamaño de elemento apropiado. La Figura 2,muestra la gráfica de deflexión contra tamaño de elemento apreciándose la estabilidad de los resultados a partir de un tamaño de elemento de 22.5 mm, siendo mucho más estable en 20 mm, por lo que este último fue el valor establecido para generar el mallado.
A partir del tamaño de elemento se establecen el resto de las propiedades de la malla (Tabla 3). En la Figura 3, se representa una vista en 3D del modelo de la viga con el mallado resultante y las condiciones de frontera, donde se aprecia las restricciones (flechas de color verde) y la carga aplicada estáticamente (flechas de color rojo).
TABLA 3 Caracteristicas de la malla empleada en el análisis
| Parámetros | Malla | Calidad | Tolerancia | Cant. de nodos | Cant. de elementos | Tamaño de elementos |
|---|---|---|---|---|---|---|
| Descripción | Sólido, Estándar | Alta | 0.05 mm | 4,340 | 2,342 | 20 mm |
Descripción del método experimental empleado
La determinación experimental de las deformaciones estáticas que permitían determinar los coeficientes de cargas dinámicas del sistema objeto de estudio bajo diferentes cargas dinámicas se efectuó mediante técnicas de extensometría eléctrica.
En la cara inferior del centro de la viga objeto de estudio se colocaron galgasextensométricas(Figura 4) configuradas en un cuarto de puente deWheatstone, con el objetivo de obtener señales de voltaje proporcionales a la deformación unitaria (considerando las deformaciones dentro del límite elástico del material), producidas por cargas estáticas de diferente magnitud.Las cargas estáticas se obtenían colocando pesos de 25 N; 400 N y 800 N en el centro de la viga y registrando el voltaje de salida (eest) del sistema de medición. De forma similar se registraba el voltaje de salida (edin) producido por las mismas cargas aplicadas dejando caer al centro de la viga los mismos pesos desde diferentes alturas, entre 0.1 y 1 m. Para cada uno de los tratamientos se efectuaron tres repeticiones. El cociente de los voltajes obtenidos, para cada una de las cargas y alturas aplicadas, permitía obtener el coeficiente de cargas dinámicas en cada caso, aplicando la expresión:
donde:
e est |
- es el voltaje registrado bajo la acción de las cargas aplicadas en forma estática; |
e din |
- es el voltaje máximo bajo la acción de las cargas aplicadas en forma dinámica (al dejar caer los pesos desde diferentes alturas); |
ε est y ε din |
- son las deformaciones unitarias correspondientes a las cargas estáticas y dinámicas, respectivamente; |
δ est y δ din |
- son esfuerzos normales correspondientes a las cargas estáticas y dinámicas, respectivamente. |
Las señales provenientes de las galgas extensométricas (del orden de los mV), eranprocesadasen un amplificador dinámico, modelo KYOWA-YA-520 con módulos de amplificación del tipo DPM-602B, siendo amplificadas hasta niveles de voltaje entre ± 5V.
La señal analógica proveniente del amplificador (Figura 5) era digitalizada en un convertidor análogo-digitalmodelo NATIONAL INSTRUMENTS - NI USB-4431e introducida a razón de 100 muestras por segundo en una computadoraportátil para su posterior procesamiento estadístico.
RESULTADOS YDISCUSIÓN
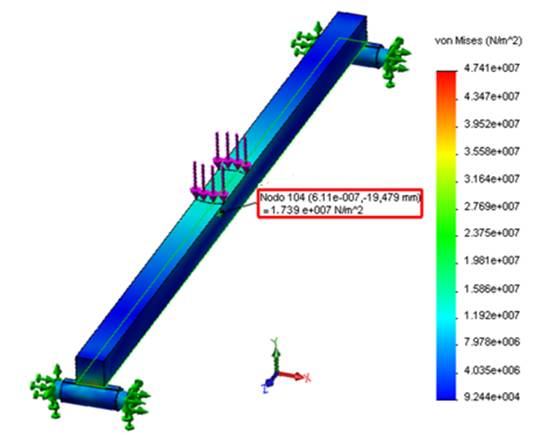
La Figura 6 muestra una de las salidas del análisis estático mediante el MEF para determinar la deformación unitaria de la viga objeto de estudio. Cuando la viga es sometida a 800 N de carga estática, se observa que el valor de la deformación unitaria es de 86.976 µstrain, mientras que el resultado del esfuerzo para ese mismo valor de carga se aprecia en la Figura 7, donde alcanzó un valor de 17.3952 MPa.
La Figura 8 muestra la deflexión estática de la viga en la dirección del eje Y, donde la deflexión máxima de la viga coincide con la flecha estática y este valor es tomado directamente de la escala, siendo igual a 0.2054 mm.
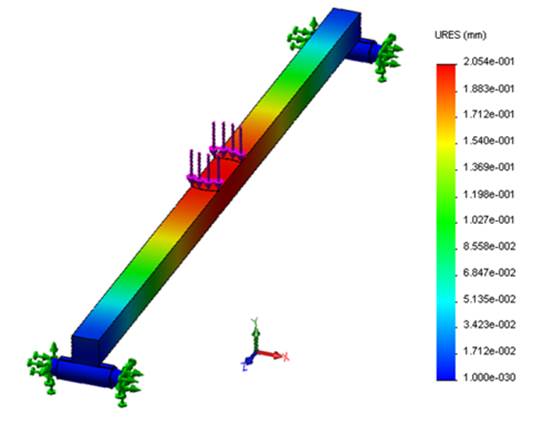
FIGURA 8 Deflexión de la viga en la dirección vertical para una carga estática de 800 N mediante análisis por el método de los elementos finitos.
Evaluación experimental de la simulación numérica
LaFigura 9muestra dos gráficascon la distribución acumulada de las deformaciones predichas por el modelo analizado mediante el MEF y los resultados experimentales. Los datos obtenidosarrojaron que la distancia máxima entre las distribuciones acumuladas de las dos muestras es de 0.03125 µstrain, donde el p-valor aproximado obtenido es mayor a 0.05, por lo que no existe diferencia estadísticamente significativa entre las dos distribuciones para un nivel de confianza del 95 %. Se observóque los datos obtenidos para los esfuerzos predichos por el modelo analizado mediante MEF y los calculados a partir de pruebas experimentalescoinciden con los resultados obtenidos para la deformación, esto se debe a que los esfuerzos están calculados a partir de las deformaciones usando la ley de Hooke.
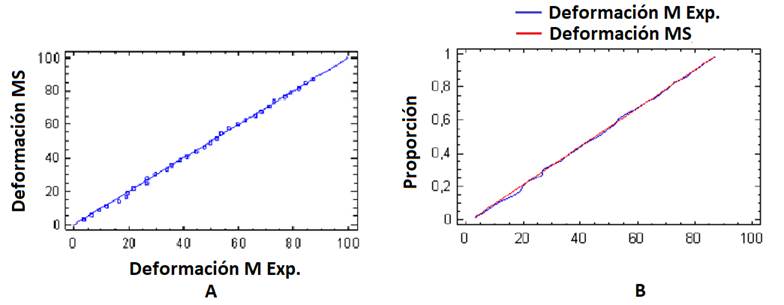
FIGURA 9 Distribución acumulada (A) y función de distribución (B) entre las deformaciones predichas por la simulación y las obtenidas experimentales.
En la Figura 10 se observa el gráfico de distribución acumulada para comparar las deflexionespredichas por el modelo analizado mediante MEF y los resultados experimentales, donde se aprecia que las distancias máximas entre las distribuciones acumuladas de las dos muestras son de 0.09375 mm. Para el comportamiento de los valores de deflexión predicha y experimental se obtuvo un p-valor aproximado de 0.998965, como es mayor que 0.05, no existe diferencia estadísticamente significativa entre las dos distribuciones para un nivel de confianza del 95 %.
Resultado de los coeficientes de cargas dinámicas por los tres métodos estudiados
En la Tabla 4, se muestran los resultados de la determinación de los coeficientes de cargas dinámicas por los diferentes métodos estudiados y la diferencia relativa existente entre los métodos y los resultados experimentales. Se aprecia que la diferencia relativa del MEF oscila entre 3.479 y 5.112 %, siendo sustancialmente inferiores a los valores obtenidos para el método analítico (MA) que van desde 21.820 hasta 27.201 %.
Los coeficientes de carga dinámica alcanzaron valores de 391.203 para el caso analítico (MA), de 501.001 para el caso experimental y un valor de 528.047 para cuando se calculan los coeficientes de cargas dinámicas a partir de los datos obtenidos de la simulación numérica por el método de los elementos finitos (MEF), con una carga de 25 N. Los mayores valores de los coeficientes de cargas dinámicas en los tres métodos de cálculo se registraron para la mayor altura estudiada (1 m) y con la menor de las cargas aplicadas (25 N). Para una misma altura de impacto se determinó que los valores más altos de coeficientes de cargas dinámicas se registran para las cargas de impacto de menor masa (25 N). A una misma altura de impacto se obtienen los coeficientes de cargas dinámicas más bajos mientras mayor es la carga que impacta.El caso de que los mayores valores de coeficiente de cargas dinámicas se registren para la menor carga se debe a que el aumento de la masa del elemento que golpea provoca mayores deflexiones por lo que disminuye el coeficiente de cargas dinámicas, debido a su relación inversamente proporcional.
TABLA 4 Diferencias relativas de los coeficientes de cargas dinámicas por ambos métodos
| Altura deimpacto; m | Cargaqueimpacta; N | Coeficientes de cargasdinámicas | Diferencia relativa | |||
|---|---|---|---|---|---|---|
| (MA) | (M Exp.) | (MEF) | MA-MExp; % | MEF- MExp; % | ||
| 0.1 | 25 | 124.397 | 159.117 | 167.62 | 21.820 | 5.344 |
| 400 | 31.864 | 42.897 | 45.141 | 25.720 | 5.231 | |
| 800 | 23 | 31.099 | 32.22 | 26.043 | 3.605 | |
| 0.2 | 25 | 175.51 | 224.61 | 236.704 | 21.860 | 5.384 |
| 400 | 44.637 | 60.243 | 63.417 | 25.905 | 5.269 | |
| 800 | 32 | 43.555 | 45.141 | 26.530 | 3.641 | |
| 0.3 | 25 | 214.725 | 274.863 | 289.677 | 21.879 | 5.390 |
| 400 | 54.44 | 73.555 | 77.441 | 25.987 | 5.283 | |
| 800 | 38.794 | 53.115 | 55.057 | 26.962 | 3.656 | |
| 0.4 | 25 | 247.787 | 317.229 | 334.335 | 21.890 | 5.392 |
| 400 | 62.704 | 84.777 | 89.265 | 26.037 | 5.294 | |
| 800 | 44.637 | 61.174 | 63.417 | 27.033 | 3.667 | |
| 0.5 | 25 | 276.916 | 354.555 | 373.679 | 21.898 | 5.394 |
| 400 | 69.986 | 94.664 | 99.682 | 26.069 | 5.301 | |
| 800 | 49.785 | 68.275 | 70.782 | 27.082 | 3.672 | |
| 0.6 | 25 | 303.251 | 388.3 | 409.25 | 21.903 | 5.395 |
| 400 | 76.569 | 103.603 | 109.1 | 26.094 | 5.306 | |
| 800 | 54.44 | 74.694 | 77.441 | 27.116 | 3.678 | |
| 0.7 | 25 | 327.468 | 419.331 | 441.96 | 21.907 | 5.396 |
| 400 | 82.623 | 111.823 | 117.76 | 26.113 | 5.309 | |
| 800 | 58.72 | 80.598 | 83.565 | 27.145 | 3.681 | |
| 0.8 | 25 | 350.009 | 448.215 | 472.406 | 21.910 | 5.397 |
| 400 | 88.258 | 119.474 | 125.821 | 26.128 | 5.312 | |
| 800 | 62.704 | 86.093 | 89.265 | 27.167 | 3.684 | |
| 0.9 | 25 | 371.468 | 475.343 | 501.001 | 21.853 | 5.398 |
| 400 | 93.55 | 126.66 | 133.393 | 26.141 | 5.316 | |
| 800 | 66.446 | 91.254 | 94.618 | 27.186 | 3.686 | |
| 1 | 25 | 391.203 | 501.001 | 528.047 | 21.916 | 5.398 |
| 400 | 98.556 | 133.457 | 140.554 | 26.151 | 5.318 | |
| 800 | 69.986 | 96.136 | 99.682 | 27.201 | 3.689 | |
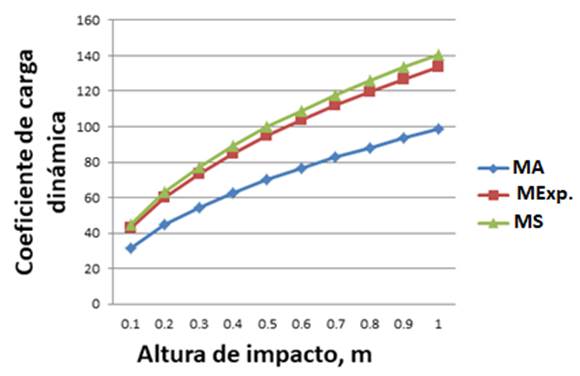
En la Figura 11 se representa el comportamiento de los coeficientes de cargas dinámicas por los tres métodos estudiados para una carga de impacto de 400 N, el rango de alturas de impacto va desde 0.2 hasta 1 m. Se observa que la curva de comportamiento obtenida mediante el MEF es la que más se acerca a la obtenida por MExp.Los resultados obtenidos mediante la simulación numérica (MEF), brindaron mejores resultados y esto se debe a la ventaja que brinda el método de los elementos finitos ante los métodos analíticos, permitiendo simular el sistema de forma más realista, teniendo en cuenta un mayor número de factores durante la simulación. Los procesos analíticos son simplificados y no dejan de ser de mucho valor práctico para el diseño de innumerables sistemas, pero tienen el inconveniente de no permitir conocer a detalle el comportamiento estructural bajo acciones reales.
Coincidiendo con los resultados obtenidos, Aparicio y Casas(1987)señalan que en la interpretación de los resultados de pruebas de cargas de impacto, es importante conocer aspectos que no se consideran en los estudios analíticos, además resulta vitalconocer los detallesdel fenómeno cuando se tienen en cuenta la deflexión de estructuras de automóviles para ver su repercusión en el confort y la seguridad de los pasajeros(Álvarez et al., 1983). Por su parteBeltrán y Cerrolaza(1989), plantean que se hace necesario recurrir a modelos de cálculo más sofisticados que permitan reproducir con más fidelidad el comportamiento real de diferentes sistemas.
CONCLUSIONES
La simulación numérica comparada con datos experimentales para las deformaciones y los esfuerzos alcanzó un p-valor mayor a 0.05, por lo que no existe diferencia estadísticamente significativa entre las dos distribuciones para un nivel de confianza del 95 %.
Para las deflexiones predichas por el modelo analizado mediante MEF y los resultados experimentales se alcanzó un p-valor aproximado de 0.99, por lo que no existe diferencia estadísticamente significativa entre las dos distribuciones.
La diferencia relativa existente entre los coeficientes de cargas dinámicas por método experimental (MExp.) y por simulación numérica(MEF) oscila entre 3.479 y 5.122%, siendo sustancialmente inferiores a los valores obtenidos para el método analítico (MA), que alcanzó valores desde 21.820 hasta 27.201%.
REFERENCES
ÁLVAREZ, R.; MOLINA, R.F.J.; DOBLARÉ, C.M.; ALARCÓN, E.: “Interacción dinámica vehículo-vía-estructura-cimiento en puentes de ferrocarril”, En: Anales de Ingeniería Mecánica, Ed. Asociación Española de Ingeniería Mecánica; Universidad de Cantabria (Dpto, vol. 1, pp. 451-460, 1983, ISBN: 0212-5072. [ Links ]
APARICIO, A.; CASAS, J.R.: “Resultados y conclusiones de las pruebas efectuadas en el paso superior de Alfonso X, en el Cinturón de Ronda de Barcelona: Una fuente de enseñanza”, Hormigón y acero, 162: 33-141, 1987. [ Links ]
BELTRÁN, F.; CERROLAZA, M.: “Análisis dinámico de estructuras sometidas a cargas no lineales”, Revista internacional de métodos numéricos para cálculo y diseño en ingeniería, 5(4): 473-502, 1989, ISSN: 1886-158X. [ Links ]
CASTRO, D.; GÜIZA, R.: Análisis del efecto de una grieta en el comportamiento estructural de una biela usando FEA, ser. Engineering Sciences [physics]/ Mechanics [physics.med-ph]/ Mechanics of the structures [physics.class-ph], Inst. Grupo de Investigación en Energía y Medioambiente (GIEMA). Universidad Industrial de Santander, Colombia, Colombia, 2017. [ Links ]
FENG, D.; AYMERICH, F.: “Finite element modelling of damage induced by low-velocity impact on composite laminates”, Composite Structures, 108: 161-171, 2014, ISSN: 0263-8223, DOI: https://doi.org/10.1016/j.compstruct.2013.09.004. [ Links ]
KONG, Y.S.; ABDULLAH, S.; OMAR, M.Z.; HARIS, S.M.: “Failure assessment of a leaf spring eye design under various load cases”, Engineering Failure Analysis, 63: 146-159, 2016, ISSN: 1350-6307, DOI: https://doi.org/10.1016/j.engfailanal.2016.02.017. [ Links ]
LIU, T.; FLECK, N.A.; WADLEY, H.N.G.; DESHPANDE, V.S.: “The impact of sand slugs against beams and plates: Coupled discrete particle/finite element simulations”, Journal of the Mechanics and Physics of Solids, 61(8): 1798-1821, 2013, ISSN: 0022-5096, DOI: https://doi.org/10.1016/j.jmps.2013.03.008. [ Links ]
MARTÍNEZ, R.A.; BOZA, M.Y.; LASTRA, M.D.; BARROSO, P.P.: “Análisis modal del sistema fruto-pedúnculo del Nim”, Revista Ciencias Técnicas Agropecuarias, 16(3): 43-46, 2007, ISSN: 1010-2760, e-ISSN: 2071-0054. [ Links ]
NADAL, E.; RÓDENAS, J.J.; SÁNCHEZ, O.E.M.; LÓPEZ, R.S.; MARTÍ, P.J.: “Sobre la utilización de códigos de elementos finitos basados en mallados cartesianos en optimización estructural”, Revista internacional de métodos numéricos para cálculo y diseño en ingeniería , 30(3): 155-165, 2014, ISSN: 0213-1315, DOI: https: //doi.org/10.1016/j.rimni.2013.04.009. [ Links ]
PISARENKO, G.S.; YAKOVLEV, A.P.: Manual de resistencia de materiales, Ed. Mir Publishers, Primera ed., Moscú, Rusia. URSS, 1979. [ Links ]
SINGH, N.K.; SINGH, K.K.: “Review on impact analysis of FRP composites validated by LS‐DYNA”, Polymer Composites, 36(10): 1786-1798, 2015, ISSN: 0272-8397, DOI: 10.1002/pc.23064. [ Links ]
UNTAROIU, C.D.; YUE, N.; SHIN, J.: “A finite element model of the lower limb for simulating automotive impacts”, Annals of biomedical engineering, 41(3): 513-526, 2013, ISSN: 0090-6964, DOI: 10.1007/s10439-012-0687-0. [ Links ]
VAVALLE, N.A.; MORENO, D.P.; RHYNE, A.C.; STITZEL, J.D.; SCOTT, G.F.: “Lateral impact validation of a geometrically accurate full body finite element model for blunt injury prediction”, Annals of biomedical engineering , 41(3): 497-512, 2013, ISSN: 0090-6964, DOI: https://doi.org/10.1007/s10439-012-0684-3. [ Links ]
WARRENDALE, P.A.: SAE Handbook. Society of Automotive Engineers, Warrendale P.A.: Metals Handbook. American Society for Metals. Materials Park. Ohio, USA., 2001. [ Links ]
XIAOFEI, W.; YINGCHUN, S.H.; XIANDONG, L.; WANG, H.; JIEGONG, W.: “Simulation of biaxial wheel test and fatigue life estimation considering the influence of tire and wheel camber”, Advances in Engineering Software, 92: 57-64, 2016, ISSN: 0965-9978, DOI: https://doi.org/10.1016/j.advengsoft.2015.11.005. [ Links ]
ZHANBIAO, L.; DI CECCO, S.; ALTENHOF, W.; THOMAS, M.; BANTING, R.; HU, H.: “Stress and fatigue life analyses of a five-piece rim and the proposed optimization with a two-piece rim”, Journal of Terramechanics, 52: 31-45, 2014, ISSN: 0022-4898, DOI: https://doi.org/10.1016/j.jterra.2014.02.002. [ Links ]
ZHAO, Y.Q.; ZANG, L.G..; CHEN, Y.Q.; LI, B.; WANG, J.: “Non-pneumatic mechanical elastic wheel natural dynamic characteristics and influencing factors”, Journal of Central South University, 22(5): 1707-1715, 2015, ISSN: 1005-9784, DOI: https://doi.org/10.1007/s11771-015-2689-1. [ Links ]
Recibido: 12 de Diciembre de 2018; Aprobado: 02 de Septiembre de 2019











 texto en
texto en