Mi SciELO
Servicios Personalizados
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Revista Ciencias Técnicas Agropecuarias
versión On-line ISSN 2071-0054
Rev Cie Téc Agr vol.28 no.4 San José de las Lajas oct.-dic. 2019 Epub 01-Dic-2019
ARTÍCULO ORIGINAL
Modelo de la interacción suelo herramienta de labranza estrecha utilizando el Método de Elementos Finitos
IUniversidad Agraria de La Habana (UNAH), Facultad de Ciencias Técnicas, Centro de Mecanización Agropecuaria (CEMA), San José de las Lajas, Mayabeque, Cuba.
La mayor parte de los estudios de la interacción suelo˗herramienta de labranza realizados, tanto experimentales como numéricos, han mostrado la influencia de las condiciones del suelo (propiedades físicas, mecánicas y dinámicas, tipo de suelo), parámetros de operación de la herramienta (profundidad de corte, velocidad de corte, aceleración) y geometría de la misma en la magnitud de las fuerzas de corte. Los mismos se han llevado a cabo con pequeños deslizamientos de la herramienta para evitar la distorsión, lo cual puede provocar problemas de convergencia durante la simulación. En este estudio, un modelo de simulación tridimensional (3D) lineal dinámico de la interacción suelo˗herramienta de labranza estrecha ha sido desarrollado mediante el método de elementos finitos (MEF) para analizar el movimiento de la herramienta de cultivo a través de un bloque de suelo tipo arcilloso limoso (ferralítico).Se utilizó el modelo elastoplástico de relación constitutiva(Drucker˗Prager)para la modelación, la cual fue realizada utilizando el software de diseño Solid Works, versión 2014y su complemento Simulation. Para una mejor conexión entre las superficies, tanto del suelo como de la herramienta de cultivo, fueron utilizados elementos de contacto y el teorema de Coulomb para lograr buen movimiento de los elementos del suelo sobre la superficie de trabajo de la herramienta. El modelo predijo el movimiento del suelo, las superficies de falla del mismo, distribución de tensiones tanto en el suelo como en la herramienta de cultivo, así como las fuerzas de corte. Se compararon los resultados del modelo de simulación con otros modelos y datos experimentales de otros autores, obteniéndose buenas predicciones y similares tendencias.
Palabras-clave: Modelo de simulación dinámico 3D; interacción suelo˗ herramienta; elementos finitos
INTRODUCCIÓN
La interacción suelo˗herramienta de labranza se caracteriza por dos fenómenos: fuerzas que surgen en la interfase suelo-herramienta (fuerzas de tracción, laterales y verticales) y desplazamiento de las partículas de suelo (Ani et al., 2014).
Una parte importante de las investigaciones relacionadas con la interacción suelo˗herramienta de labranza ha sido enfocada al desarrollo de modelos de simulación para predecir las fuerzas de corte bajo diferentes condiciones de suelo, geometría de la herramienta y parámetros de operación (Armin et al., 2014). Efectos bastante significativos de esas condiciones y parámetros en las fuerzas de corte han sido demostrados experimentalmente en varios trabajos de investigación. No obstante, los estudios experimentales de la interacción suelo˗herramienta son caros y sus resultados dependen de la precisión de los instrumentos de medición.
El MEF ha sido utilizado con gran aceptación a escala internacional en la simulación computacional de la interacción suelo-herramienta de labranza, debido a su potencial para describir la misma en tres dimensiones (Herrera, 2006; Armin et al., 2014b; Tagar et al., 2015).
Para la simulación de la interacción suelo-herramienta de labranza mediante el MEF se han realizado numerosas investigaciones en el ámbito internacional, entre ellas las de Swick y Perumpral (1988); Mouazen y Neményi(1999); Abo et al.(2003, 2004); Brown (2012); Bentaher et al.(2013); Armin et al.(2014, 2015, 2016); Elbashir et al.(2014); Neisy (2014); He et al.(2016), con el objetivo de desarrollar modelos, en dos ó tres dimensiones, tanto lineales como no lineales; elásticos, plásticos y elastoplásticos, para la predicción de los esfuerzos del suelo sobre la herramienta de cultivo, la influencia de la geometría en las fuerzas de corte, así como el consumo energético de las mismas. La mayoría de ellos se han realizado con pequeños desplazamientos de la herramienta y a bajas velocidades de corte.
Modelos dinámicos de simulación de la interacción suelo˗herramienta por el MEF han sido desarrollados por (Swick y Perumpral, 1988; Dechao y Yusu, 1992; Abo et al., 2003)en los cuales se han tenido en cuenta la velocidad de corte, el nivel de tensiones y la aceleración. Cuando se analiza la interacción suelo-herramienta de labranza como un proceso dinámico, se consideran los posibles efectos de inercia referidos a la influencia de la masa de suelo y los del grado de deformación. En estos casos se incorpora el tiempo dentro de la formulación del modelo constitutivo (Herrera, 2006).
El objetivo general de este estudio es desarrollar un modelo de simulación 3Ddinámicodel proceso de interacción suelo˗herramienta de labranza, que permita el análisis del movimiento de la herramienta a través del suelo, la distribución y magnitud de las tensiones y deformaciones, así como las fuerzas de corte.
MÉTODOS
Modelo para el suelo. En el presente estudio, la interacción suelo˗herramienta es modelada mediante la función de fluencia de Drucker˗Prager lineal, la cual se expresa como:
Donde:
σ1, σ2, σ3 |
- son los esfuerzos principales máximos, intermedios y mínimos |
t |
- es el esfuerzo desviador y se calcula por: |
K es el coeficiente que relaciona los esfuerzos desviadores obtenidos en triaxial extensión con los obtenidos en triaxial compresión, calculándose como:
Donde:
φ |
- es el ángulo de fricción interna |
p |
- es el esfuerzo normal que actúa sobre el suelo y se define como: |
Β ángulo que define la pendiente de la superficie de fluencia lineal, el cual está referido comúnmente al ángulo de fricción interna del material en el modelo de Drucker˗Prager Extendido(Figura 1)y se calcula por:
q son las tensiones equivalentes de Von Mises y se expresan por:
r 3 es el esfuerzo desviador, el cual se calcula por:
La cohesión d, cuando el endurecimiento se define por ésta, se calcula como:
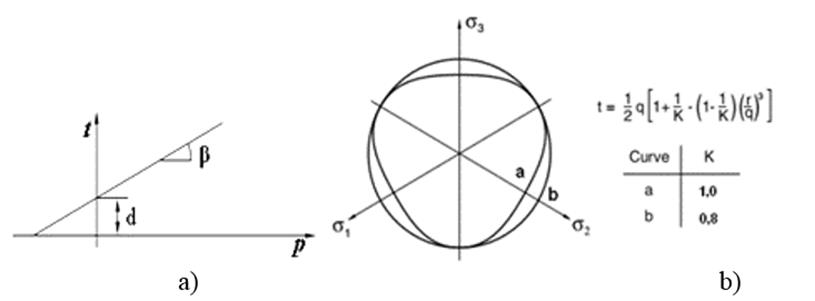
FIGURA 1 Criterio de Fluencia del Modelo Drucker-Prager extendido. a) Plano meridional; b) Plano de tensiones principales.
Propiedades del suelo. El suelo se clasificó como ferralítico rojo típico según la Segunda Clasificación Genética de los Suelos en Cuba(Hernández et al., 1975), como Oxisol(Cid et al., 2011)y como Rhodic Ferralsol Hernández et al. (2015), con una densidad de 1200kg·m-3, índice de plasticidad de 36,2% y contenido de materia orgánica 2,7%. El módulo de elasticidad se determinó como la pendiente de una recta tangente a la curva esfuerzo-deformación en su tramo recto. El coeficiente de Poisson se determinó mediante la ecuación
La cohesión y el ángulo de fricción interna fueron determinados mediante la solución gráfica de Mohr. Según el triángulo de textura del suelo García de la Figal (2013), el suelo en estudio se clasifica como arcilloso poco denso.
La Tabla 1 muestra las propiedades y parámetros del suelo requeridos por el modelo de elementos finitos.
TABLA 1 Propiedades y parámetros requeridos por el modelo FEM
| Propiedad o parámetro | Símbolo | Dimensión |
|---|---|---|
| Ángulo de fricción interna | 33º | |
| Módulo de elasticidad | 5 000 000 Pa | |
| Coeficiente de Poisson | 0,394 | |
| Tensión de flexión del suelo |
|
130 000 Pa |
| Ángulo de dilatación | 0º | |
| Cohesión | 15 000 Pa | |
| Resistencia a los esfuerzos cortantes | 200 000 Pa | |
| Módulo cortante | 1 793 400 Pa | |
| Tipo de suelo | Isotrópico elástico lineal | |
| Límite de tracción del suelo |
|
30 000 Pa |
| Límite de compresión del suelo |
|
500 000 Pa |
| Límite elástico del suelo |
|
42 000 Pa |
| Humedad del suelo | 27% |
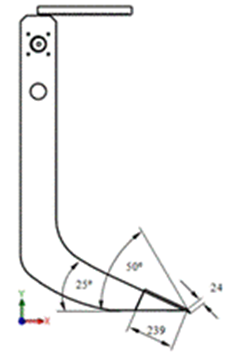
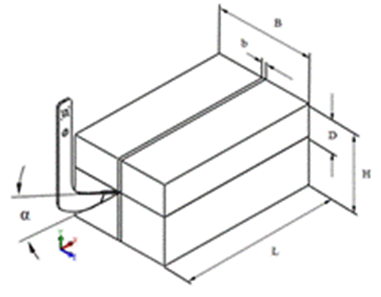
Modelo de elementos finitos . Un modelo de simulación en 3D dinámico de la interacción herramienta de labranza-suelo en elementos finitos ha sido desarrollado utilizando el software de diseño Solid Works. Está formado por la herramienta de labranza (brazo escarificador vibratorio curvo) con perfil logarítmico, al cual se le adiciona un mecanismo vibrador con masas desbalanceadas y es considerada como un cuerpo rígido discreto (Figura 2). El bloque de suelo es deformable en interacción con el brazo escarificador (Fig.3), tiene una longitud (L) de 2m, su ancho (B) es de 1m, la altura (H) es de 1m. El ancho del prisma de suelo cortado por la herramienta coincide con el ancho de la reja del brazo (b=0,041m). La profundidad de trabajo del brazo (D) es de 0,40m y el ángulo de corte es de 25 grados.
Se asume que el aumento de las dimensiones del prisma de suelo cortado más allá de las asignadas no afecta las fuerzas de corte (Bentaher et al., 2013)(Ibrahmi et al., 2014). La interacción herramienta-suelo se modeló tangencialmente a la superficie de ataque con modelo de contacto superficie a superficie.
Modelación del contacto. En el proceso de corte del bloque de suelo, la modelación del contacto es muy complicada, pues una de las superficies, la del prisma de suelo, no existe inicialmente en el modelo, sino que se forma en la medida que transcurre el proceso (Figura 4). La parte del bloque de suelo que es convertida en prisma se desliza sobre la superficie de ataque de la herramienta, provocando una zona de contacto con alta fricción entre ambas superficies y altas tensiones.
Los problemas de contacto son modelados por elementos finitos usando superficies básicas de contacto (Rodríguez, 2001). Con el desplazamiento de la herramienta hacia el bloque de suelo, ocurre gradualmente la formación del prisma, en el cual la superficie 1 pasa a ser la superficie labrada, y la superficie 2 entra en contacto con la superficie 3 (superficie de ataque de la herramienta de labranza).
A medida que se forma la superficie 3, los elementos de contacto de la misma se activan como una superficie de contacto, que se desplazará sobre una línea de deslizamiento definida por los mismos, los cuales conforman una superficie de contacto entre dos cuerpos deformables (Figura 5).
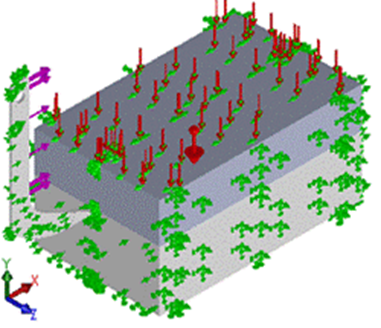
Cargas y condiciones de contorno. Las condiciones de contorno al modelo se establecieron en función de las cargas actuantes. Sobre el bloque de suelo actúa la aceleración de la gravedad (9,81 m·s-2) y la presión atmosférica (101325 Pa) y tiene restricciones de movimiento lateralmente (eje Z) y por su parte inferior (eje Y). La herramienta de labranza se desplaza a velocidad constante de 1,2 m.s-1 en la dirección positiva del eje X (Figura 6), con frecuencia de las vibraciones del mecanismo vibrador de 14Hz la fuerza de tracción aplicada a la misma fue de 15000 N y el prisma de suelo cortado se desplaza sobre la superficie de ataque de la reja.
Discretización del modelo. La discretización general del modelo se realizó con un tamaño de elementos (e) máximo de 0,03 m, tamaño mínimo de 0,006 m y se utilizó el método iterativo de Newton-Raphson. Las superficie en contacto, tanto de la herramienta como del prisma de suelo cortado se discretizaron aplicando control de mallado, con tamaño de elemento de 0,004 m (Figura 7).
RESULTADOS Y DISCUSIÓN
Los resultados del modelo de simulación tridimensional dinámico presentado proporcionaron información respecto a fuerzas de corte, tensiones, deformaciones y desplazamientos del suelo y la herramienta. El modelo simuló el desplazamiento y las vibraciones del brazo escarificador con la frecuencia y amplitud seleccionadas, así como el avance del prisma de suelo cortado sobre la superficie de ataque de la reja.
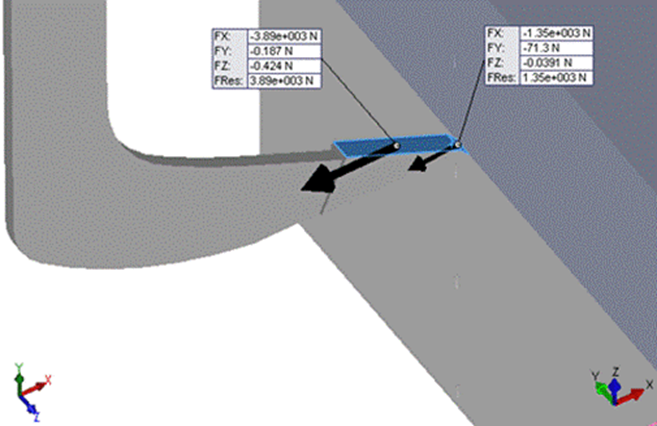
Fuerzas en la herramienta de labranza. La Figura 8 muestra la magnitud y dirección de las fuerzas resultantes obtenidas como resultado de la interacción de la herramienta de labranza con el bloque de suelo y de su avance a través de la misma.
Como puede observarse, los mayores valores de la fuerza de tracción están en la punta (Fx=-1350 N) y superficie de ataque de la herramienta (Fx=-3890 N), en la dirección del movimiento de avance de ésta y tienen signo negativo. Estos valores son similares a los obtenidos por otros autores en investigaciones anteriores ( Moeinfar et al., 2014).
La magnitud de las fuerzas resultantes está determinada por el tipo de suelo utilizado en la modelación (Davoudi et al., 2008). La fuerza de tracción máxima (Fx) es considerada como la fuerza necesaria para la falla del bloque de suelo delante de la herramienta y como la resistencia del suelo a ser cortado por la misma(Elbashir et al., 2014b).
Tensiones en la herramienta de labranza. La Figura 9 muestra el progreso de las tensiones de von Mises cuando el brazo escarificador labora el suelo. El modelo simula de forma adecuada el proceso de interacción suelo-herramienta.
Las tensiones aumentan durante la fase inicial de contacto entre la herramienta de labranza y el suelo y posteriormente se estabilizan, lo cual coincide con estudios realizados y datos experimentales publicados por otros investigadores (Mouazen y Neményi, 1999b; Abo et al., 2004b; Bentaher et al., 2013b; Chen et al., 2013); (Ibrahmi et al., 2014). Estos resultados muestran la validez del modelo de simulación implementado.
Tensiones normales en dirección X en la punta de la herramienta. Cuando comienza el contacto con el suelo, las tensiones normales en dirección X en la punta de la herramienta (Figura 10) tienen un valor mínimo de 0,035MPa, aumentando de forma asintótica (Mouazen y Neményi, 1999b). A medida que avanza el brazo sobre el bloque de suelo, las tensiones alcanzan un máximo valor dado (0,28MPa), disminuyendo nuevamente hasta estabilizarse en un valor promedio de aproximadamente 0,15 MPa. Esto se debe, en lo fundamental, al movimiento oscilatorio del brazo y a la resistencia del suelo.
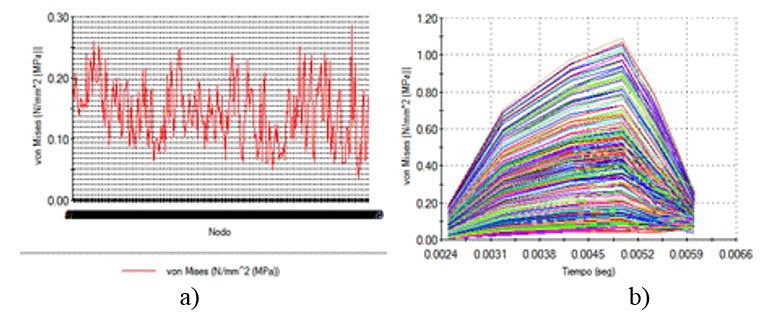
FIGURA 10 Tensiones normales en dirección X en la punta de la herramienta de labranza a) Estáticas en los nodos b) dinámicas.
Tensiones en la superficie de ataque. Las tensiones en la superficie de ataque (Figura 11) aumentan desde un valor mínimo de 0,14 MPa hasta alcanzar un máximo valor de 8,55 MPa, luego se estabilizan en aproximadamente 3,92 MPa. Estos valores promedio de tensiones son mayores que en la punta de la herramienta debido a la mayor área de contacto que existe entre esta superficie y el bloque de suelo.

FIGURA 11 Tensiones normales en dirección X en la superficie de ataque de la herramienta de labranza a) Estáticas en los nodos b) dinámicas.
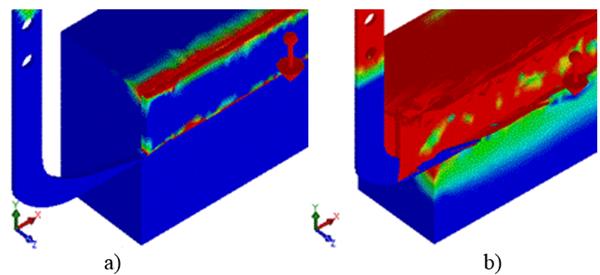
Validación del modelo. Para la validación del modelo de simulación implementado se examinó la validez de las superficies de falla predefinidas por Abo et al. (2003a) en el plano vertical (plano XY) analizando la distribución de tensiones tangenciales a cero desplazamiento de la herramienta de labranza (Figura 12a) y a 300 mm de desplazamiento (Figura 12b).
Los contornos continuos de la distribución de tensiones tangenciales a lo largo de las superficies de falla predefinidas (Figura 12b), revelan la validez de las mismas al ser aplicada sobre el modelo la fuerza de gravedad.
CONCLUSIONES
Un modelo de simulación dinámico tridimensional (3D) de la interacción suelo-herramienta de labranza estrecha utilizando el método de elementos finitos ha sido implementado.
El modelo elastoplástico de relación constitutiva de Drucker-Prager utilizado en la simulación fue capaz de predecir el comportamiento del suelo al interactuar con la herramienta de labranza.
El concepto de superficies de falla predefinidas ha sido mostrado ser adecuado para el modelado en tres dimensiones de los problemas de la interacción suelo-herramienta de labranza.
Los valores de las fuerzas resultantes del modelo son similares a los encontrados en la literatura consultada y son mayores en la superficie de trabajo de la herramienta de labranza.
Los valores de las tensiones resultantes de la simulación concuerdan con los obtenidos por otros autores en investigaciones anteriores.
REFERENCES
ABO, E.M.; HAMILTON, R.; BOYLE, J.T.: “3D Dynamic analysis of soil-tool interaction using the finite element method”, Journal of Terramechanics, 40(1): 51-62, 2003a, ISSN: 0022-4898. [ Links ]
ABO, E.M.; HAMILTON, R.; BOYLE, J.T.: “3D Dynamic analysis of soil-tool interaction using the finite element method”, Journal of Terramechanics , 40(1): 51-62, 2003b, ISSN: 0022-4898. [ Links ]
ABO, E.M.; HAMILTON, R.; BOYLE, J.T.: “Simulation of soil-blade interaction for sandy soil using advanced 3D finite element analysis”, Soil and Tillage Research, 75(1): 61-73, 2004a, ISSN: 0167-1987. [ Links ]
ABO, E.M.; HAMILTON, R.; BOYLE, J.T.: “Simulation of soil-blade interaction for sandy soil using advanced 3D finite element analysis”, Soil and Tillage Research , 75(1): 61-73, 2004b, ISSN: 0167-1987. [ Links ]
ANI, A.O.; UZOEJINWA, B.B.; EZEAMA, O.A.; UGWU, S.N.; OHAGWU, C.J.; ODIGBOH, E.U.: “Soil Bin Facility for Soil-machine Interaction Studies”, En: Department of Agricultural and Bioresources Engineering, University of Nigeria , Nsukka, International Soil Tillage Research Organization (ISTRO) Nigeria Symposium, Akure , November 3 - 6, Nsukka, Nigeria, pp. 110 - 124, 2014. [ Links ]
ARMIN, A.; FOTOUHI, R.; SZYSZKOWSKI, W.: “On the FE modeling of soil-blade interaction in tillage operations”, Finite elements in analysis and design, 92: 1-11, 2014a, ISSN: 0168-874X. [ Links ]
ARMIN, A.; FOTOUHI, R.; SZYSZKOWSKI, W.: “On the FE modeling of soil-blade interaction in tillage operations”, Finite elements in analysis and design , 92: 1-11, 2014b, ISSN: 0168-874X. [ Links ]
ARMIN, A.; FOTOUHI, R.; SZYSZKOWSKI, W.: “On the FE modeling of soil-blade interaction in tillage operations”, Finite elements in analysis and design , 92: 1-11, 2014c, ISSN: 0168-874X. [ Links ]
ARMIN, A.; FOTOUHI, R.; SZYSZKOWSKI, W.: “3D Finite Element Analysis for Mechanics of Soil-Tool Interaction”, World Academy of Science, Engineering and Technology, International Journal of Mechanical, Aerospace, Industrial, Mechatronic and Manufacturing Engineering, 9(5): 843-848, 2015. [ Links ]
ARMIN, A.; SZYSZKOWSKI, W.; FOTOUHI, R.: “3D Finite Element Analysis of Curved Blade’s Mechanics in Farming Tillage Operations”, En: World Congress on Engineering 2016 Vol II WCE 2016, June 29 - July 1, London, U.K., 2016. [ Links ]
BENTAHER, H.; IBRAHMI, A.; HAMZA, E.; HBAIEB, M.; KANTCHEV, G.; MAALEJ, A.; ARNOLD, W.: “Finite element simulation of moldboard-soil interaction”, Soil and Tillage Research , 134: 11-16, 2013a, ISSN: 0167-1987. [ Links ]
BENTAHER, H.; IBRAHMI, A.; HAMZA, E.; HBAIEB, M.; KANTCHEV, G.; MAALEJ, A.; ARNOLD, W.: “Finite element simulation of moldboard-soil interaction”, Soil and Tillage Research , 134: 11-16, 2013b, ISSN: 0167-1987. [ Links ]
BROWN, O.: Finite element analysis of blade-formation interactions in excavation, MSc. Thesis, Paper 5134, USA, 2012. [ Links ]
CHEN, Y.; MUNKHOLM, L.J.; NYORD, T.: “A discrete element model for soil-sweep interaction in three different soils”, Soil and Tillage Research , 126: 34-41, 2013, ISSN: 0167-1987. [ Links ]
CID, L.G.; LÓPEZ, T.; GONZÁLEZ, F.; HERRERA, J.; RUIZ, M.E.: “Propiedades físicas de algunos suelos de Cuba y su uso en modelos de simulación”, Revista Ciencias Técnicas Agropecuarias, 20(2): 42-46, 2011, ISSN: 1010-2760, E-ISSN: 2071-0054. [ Links ]
DAVOUDI, S.; ALIMARDANI, R.; KEYHANI, A.; ATARNEJAD, R.: “A two dimensional finite element analysis of a plane tillage tool in soil using a non-linear elasto-plastic model”, American-Eurasian J. Agric. & Environ. Sci, 3(3): 498-505, 2008. [ Links ]
DECHAO, Z.; YUSU, Y.: “A dynamic model for soil cutting by blade and tine”, Journal of terramechanics, 29(3): 317-327, 1992, ISSN: 0022-4898. [ Links ]
ELBASHIR, M.A.; ZHAO, Z.; HEBEIL, E.A.; LI, X.Y.: “Comparative Finite Element Analysis of the Effects of Tillage Tool Geometry on Soil Disturbance and Reaction Forces”, Research Journal of Applied Sciences, Engineering and Technology, 7(15): 3145-3149, 2014a, ISSN: 2040-7459; E-ISSN: 2040-7467. [ Links ]
ELBASHIR, M.A.; ZHAO, Z.; HEBEIL, E.A.; LI, X.Y.: “Comparative Finite Element Analysis of the Effects of Tillage Tool Geometry on Soil Disturbance and Reaction Forces”, Research Journal of Applied Sciences, Engineering and Technology, 7(15): 3145-3149, 2014b, ISSN: 2040-7459; E-ISSN: 2040-7467. [ Links ]
GARCÍA DE LA FIGAL, C.A.E.: Maquinaria Agrícola II, Inst. Universidad Agraria de La Habana, Facultad de Ciencias Técnicas, Departamento de Ingeniería, Apuntes de clases, San José de las Lajas, Mayabeque, Cuba, 2013. [ Links ]
HE, C.; YOU, Y.; WANG, D.; WANG, G.; LU, D.; KAJI, M.J.: “The effect of tine geometry during vertical movement on soil penetration resistance using finite element analysis”, Computers and Electronics in Agriculture, 130: 97-108, 2016, ISSN: 0168-1699. [ Links ]
HERNÁNDEZ, A.; PÉREZ, J.; BOSCH, D.; CASTRO, N.: Clasificación de los suelos de Cuba 2015 . edit. Ediciones INCA, Mayabeque, Cuba , 2015, 93 p, Ed. IINCA, San José de las Lajas, Mayabeque, Cuba, 2015, ISBN: 978-959-7023-77-7. [ Links ]
HERNÁNDEZ, A.; PÉREZ, J.M.; ASCANIO, O.; ORTEGA, F.; ÁVILA, L.; CÁRDENAS, A.; MARRERO, A.: “II Clasificación genética de los suelos de Cuba”, Revista Agricultura, 8(1): 47-69, 1975. [ Links ]
HERRERA, S.M.: Simulación del comportamiento mecánico de los suelos Ferralíticos rojos mediante el método de elementos finitos , 107pp, Universidad Agraria de La Habana, PhD. Thesis, San José de las Lajas. Habana, Cuba, 109 p., 2006. [ Links ]
HIBBIT, K.: Abaqus Analysis User´s, Volume III, Materials, Inst. Hibbitt, Karlsson, and Sorensen, Inc., Pawtucket, Rhode Island, 180 p., 2008. [ Links ]
IBRAHMI, A.; BENTAHER, H.; MAALEJ, A.: “Soil-blade orientation effect on tillage forces determined by 3D finite element models”, Spanish Journal of Agricultural Research, 12(4): 941-951, 2014, ISSN: 2171-9292. [ Links ]
MOEINFAR, A.; MOUSAVI, S.S.R.; KALANTARI, D.: “Influence of tillage depth, penetration angle and forward speed on the soil/thin-blade interaction force”, Agricultural Engineering International: CIGR Journal, 16(1): 69-74, 2014, ISSN: 1682-1130. [ Links ]
MOUAZEN, A.M.; NEMÉNYI, M.: “Finite element of subsoiler cutting in non-homogeneous sandy loam soil”, Soil & Tillage Research, 51: 1-15, 1999a, ISSN: 0167-1987. [ Links ]
MOUAZEN, A.M.; NEMÉNYI, M.: “Finite element of subsoiler cutting in non-homogeneous sandy loam soil”, Soil & Tillage Research, 51: 1-15, 1999b, ISSN: 0167-1987. [ Links ]
NEISY, I.: “Introduction to the study of soil-tool modelling”, Walia journal (Iran), 30(1): 31-34, 2014, ISSN: 1026-3861. [ Links ]
SWICK, W.C.; PERUMPRAL, J.: “A model for predicting soil-tool interaction”, Journal of Terramechanics , 25(1): 43-56, 1988a, ISSN: 0022-4898. [ Links ]
SWICK, W.C.; PERUMPRAL, J.: “A model for predicting soil-tool interaction”, Journal of Terramechanics , 25(1): 43-56, 1988b, ISSN: 0022-4898. [ Links ]
TAGAR, A.A.; CHANGYING, J.; ADAMOWSKI, J.; MALARD, J.; QI, C.S.; QISHUO, D.; ABBASI, N.A.: “Finite element simulation of soil failure patterns under soil bin and field testing conditions”, Soil and Tillage Research , 145: 157-170, 2015, ISSN: 0167-1987. [ Links ]
Recibido: 20 de Enero de 2019; Aprobado: 02 de Septiembre de 2019











 texto en
texto en