ARTÍCULO

 

Un estudio exploratorio de los esquemas que emplean los alumnos de bachillerato para validar resultados matemáticos

 

An exploratory study of schemes used by senior high school students to validate mathematic results

 

 

Dr. Víctor Larios Osorio

Universidad Autónoma de Querétaro, México [e-mail]

 

 

---

RESUMEN

Las matemáticas, como cuerpo de conocimiento científico, están conformadas no sólo por un conjunto de resultados que aparecen en libros y revistas, sino también por métodos empleados para descubrir, construir, añadir esos resultados y validar los resultados. Este último proceso tiene como herramienta la llamada demostración matemática, la cual vale la pena ser incluida en el proceso educativo. Para la realización del estudio se aplicaron dos pruebas en las que debían justificar sus resultados a una muestra aleatoria estratificada. Sin embargo, los alumnos de bachillerato (15-18 años) incluidos en el estudio no emplearon de manera natural la demostración. Es por ello que la Universidad Autónoma de Querétaro (UAQ), a fin de buscar medios para el aprendizaje de la validación matemática ha llevado a cabo un estudio diagnóstico en su Escuela de Bachilleres para detectar las estrategias utilizadas por los alumnos y así poder proponer a futuro medios didácticos para disminuir la distancia entre lo que hacen y lo que se pretende que conozcan. El resultado fundamental es la descripción de la práctica argumentativa de elección preferente por los estudiantes y la identificación que los esquemas en que se agrupan.

Palabras clave: Instrucción matemática, conceptos matemáticos, pensamiento abstracto, métodos deductivos, aprendizaje.

---

ABSTRACT

Mathematics, as a body of scientific knowledge, includes not only a set of concepts and theories described in books and scientific journals but a procedural knowledge used for solving problems and proving the resulting solution. There is a tool for proving solutions, the so-called mathematical proof, which is worth to be included in the educational process. To complete the study herein described a random stratified sample was selected and given a test demanding to explain the answers given. However, high school students (15-18 years old) do not rely on the use of the known proof scheme. For that reason, a diagnostic study was carried out at the Autonomous University of Querétaro (UAQ) in order to identify the strategies the students are currently following and finding ways to teach such mathematical proof scheme. The findings are a description of individual students' argumentative practices and the identification and grouping of the most frequently used proof scheme.

Keywords: mathematics instruction, mathematical concepts, abstract reasoning, deductive methods, learning.

---

 

 

INTRODUCCIÓN

Lo que comúnmente se entiende por demostración matemática es parte del conocimiento científico matemático que se ha constituido como medio para validar los saberes relacionados con esta disciplina, es decir, como parte del proceso de construcción de la ciencia matemática. El contenido de esta ciencia ha ido cambiando bajo la influencia de los desarrollos filosóficos, matemáticos, técnicos y científicos, por no decir que también de la ontología de los objetos matemáticos y la semiótica involucrada. Es decir, la idea de demostración, los requisitos para aceptar una, el rigor utilizado, no han sido estáticos ni absolutos. Además, en la práctica los matemáticos no están interesados o no necesitan pensar en esto para llevar a cabo su trabajo (Bloch, 2000; Bourbaki, 1972), pero no quedan exentos de estas influencias al desarrollarse académica y profesionalmente en ambientes sociales específicos.

Ahora bien, la demostración, como medio de validación matemático, no puede ser una referencia absoluta y única en el campo de la educación matemática, ya que, en este proceso, desde la perspectiva de los alumnos, intervienen aspectos cognitivos, semióticos y socio-culturales que están involucrados en los procesos educativos. La validación del conocimiento matemático es una parte epistemológicamente importante de la construcción del mismo, por lo que es necesaria su inclusión en el aprendizaje de las Matemáticas.

Así que, si se busca que los alumnos aprendan matemáticas como parte del aprendizaje del desarrollo científico, es necesario considerar en la enseñanza no sólo el resultado matemático (en este caso la demostración como producto), sino también el proceso metodológico que lleva a la construcción del conocimiento científico (que sería el proceso de demostrar como parte de la validación del conocimiento). Ambos aspectos deben ser tomados en cuenta como parte de un mismo proceso.

En términos curriculares, en el nivel educativo medio en México (alumnos de 12 a 18 años) se han incorporado algunas ideas al respecto en las instituciones, de tal manera que en la primera parte (nivel medio básico) está planteado como una competencia a desarrollarse: "Validar procedimientos y resultados. Consiste en que los alumnos adquieran la confianza suficiente para explicar y justificar los procedimientos y soluciones encontradas, mediante argumentos a su alcance que se orienten hacia el razonamiento deductivo y la demostración formal." (SEP, 2011, pág. 23).

Mientras que en la segunda parte de ese nivel (bachillerato) se incluye como una de las competencias que el alumno debe alcanzar: "Argumenta la solución obtenida de un problema, con métodos numéricos, gráficos, analíticos o variacionales, mediante el lenguaje verbal, matemático y el uso de las tecnologías de la información y la comunicación." (SEP, 2008, pág. 22).

Sin embargo, precisamente uno de los aspectos cognitivos a considerarse en la escuela es que los alumnos no validan el conocimiento matemático de "manera científica" a su ingreso en el nivel medio, sino que recurren a otros medios para ello. Entonces existe una "distancia" entre lo que hacen los alumnos y lo que supuestamente deberían hacer hacia el final de su vida escolar.

En este sentido se requiere incluir la validación matemática en la escuela, vinculada con la demostración, y poner no sólo el énfasis en el rigor sino en la comprensión de los procesos cognitivo-matemáticos y de los resultados que proporciona el alumno. Es por ello que también es preciso identificar lo que hacen los estudiantes para así determinar y planear en términos escolares hacia dónde avanzar para lograr el desarrollo de las competencias mencionadas y del aprendizaje de procesos matemáticos complejos.

En este sentido en la Universidad Autónoma de Querétaro (UAQ) se han trabajado proyectos que han permitido observar que los alumnos del nivel medio pueden argumentar matemática de manera progresiva y adecuada al analizar actividades diseñadas con una finalidad específica y que consideran un esquema reflexivo como base (Arellano, 2013; Avilés, 2014). Dichas actividades estuvieron asociadas a conceptos que se incluyen en los currículos oficiales, pero se les dio más énfasis a procesos como la observación, la argumentación y la experimentación.

Para determinar la situación de los alumnos de la Escuela de Bachilleres de la Universidad Autónoma de Querétaro se llevó a cabo un estudio diagnóstico orientado a determinarlos tipos de argumentos que escogen los alumnos para validar afirmaciones matemáticas. La información derivada de este estudio ha proporcionado algunas bases para sugerir cambios en el diseño curricular y el diseño instruccional específico de cada curso.

A continuación se describe el proceso metodológico llevado a cabo para dicho diagnóstico.

 

MÉTODOS

El proyecto se diseñó para obtener información diagnóstica del alumnado de la Escuela de Bachilleres de la UAQ, por lo que se llevó a cabo un estudio cuantitativo tomando una muestra representativa en los dos principales planteles de la institución, que se encuentran en la zona metropolitana de la ciudad de Querétaro, capital del Estado homónimo y sitio de la sede principal de la UAQ. Estos planteles (conocidos por "Sur" y "Norte" por su ubicación geográfica) agrupan a poco más de 4,100 estudiantes que representan la mayor parte de la población estudiantil de la institución (el 71.2% de los poco más de 5,800 alumnos que atiende en total en sus siete planteles repartidos en el Estado).

Con base en lo anterior se seleccionó una muestra aleatoria de manera estratificada, tomando de cada grupo una cantidad fija de alumnos dependiendo del grado, el turno y el plantel. Se contó con el apoyo de las autoridades de la institución y se tuvo acceso a las listas de los grupos. A los alumnos seleccionados se les invitó a participar y se les aplicó un "examen diagnóstico" tipo encuesta a 373 estudiantes de los dos planteles mencionados.

El instrumento para la recolección de la información fue un examen diagnóstico de diez reactivos, algunos de opción múltiple y otros para respuestas abiertas, que tenían diversas orientaciones. La aplicación duró, en todos los casos, una hora como máximo y se realizó durante la jornada normal de clases en sus respectivos planteles. Los alumnos que asistieron estuvieron en salones normales (con butacas) y no utilizaron calculadoras (no se les pidió ni se les prohibió). Fueron organizados según el grado académico.

Dado el tamaño de la muestra y el compromiso de respetar los datos personales de los alumnos participantes, no se les dio un seguimiento posterior. No obstante, uno de los propósitos de estos resultados es que sirvan de base para un estudio posterior en la misma Escuela de Bachilleres.

Es necesario aclarar que, dado el interés institucional, algunos reactivos estaban orientados a temas relacionados con las dificultades del aprendizaje en Álgebra y no a la identificación de procesos de validación, por lo que en este artículo sólo se consideran dos de esos reactivos, los cuales se describen a continuación.

El primer reactivo es de tipo de opción múltiple y contiene una consigna al final para que los alumnos expliquen la razón por la que hicieron la selección:

1. Cuando una expresión que está dentro del paréntesis se eleva a una potencia, todo lo que está dentro del paréntesis es la base. A partir del razonamiento anterior selecciona la afirmación correcta y escribe el inciso entre los paréntesis:

a) (2y²)³ = 6y⁵
b) (2y²)³ = 2y⁶
c) (2y²)³ = 6y⁶
d) (2y²)³ = 8y⁶
e) (2y²)³ = (2y²) (2y²) (2y²) = 8y⁶

Explica por qué escogiste la opción:

Es importante hacer notar que hay dos opciones correctas (d y e), por lo que se les indicó a los participantes que podían seleccionar más de una. La diferencia es que en una opción no tiene el desarrollo algebraico (la d) y en la otra sí aparece (la e). Con la consigna final se esperaba que los alumnos se vieran forzados a justificar la elección realizada y la preferencia entre esas dos opciones en función de la presencia o no de dicho desarrollo.

El reactivo 2, que no fue de opción múltiple, establecía lo siguiente (figura 1):

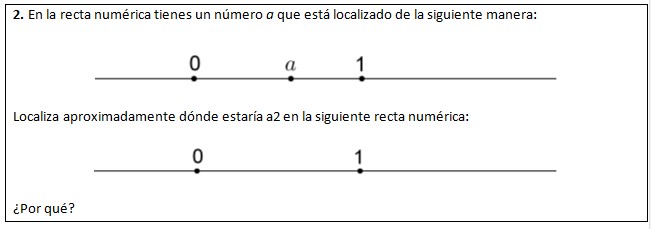
Fig 1. Con esto se esperaba que los alumnos señalaran un punto entre el 0 y la posición de a, justificando su elección de manera explícita.

 

RESULTADOS Y DISCUSIÓN

Como ya se mencionó, la necesidad de enfocarse en el estudio de los argumentos que da un alumno para justificar sus resultados viene apoyada de las exigencias sociales plasmadas en las reformas educativas recientemente realizadas en todos los niveles de escolaridad en México y que se evidencian en competencias para validar resultados y argumentar.

Al tomar el primer reactivo considerado se hizo el conteo de las opciones seleccionadas de acuerdo al gráfico 1:

Gráfico 1. Porcentajes de selección de cada opción del reactivo 1 por el nivel académico

Lo que se observa a primera vista es que las dos opciones esperadas (d y e) fueron las más seleccionadas, sin embargo, llamó la atención la ocurrencia son los siguientes hechos:

• La preferencia por la opción que tiene el desarrollo algebraico (opción e) disminuye conforme aumenta el nivel escolar, a diferencia de la preferencia por la opción sin desarrollo algebraico (opción d) que aumenta. Esto podría indicar que existe una maduración en el uso de los símbolos matemáticos.
• Se nota un aumento sustancial en la selección simultánea de las dos opciones en el tercer año, pasando de un 3.16% aproximadamente a un 10.8%.
• Es interesante notar que las opciones a y b, aunque no tienen mucha preferencia, mantienen un porcentaje a lo largo de los tres niveles.
• El inciso a, de hecho, contiene el error común de las potencias que se suman en lugar de multiplicarlas.
• El inciso b parecería el más inverosímil, pero muestra cómo existe la concepción errónea de que la potencia no afecta al coeficiente.
• El inciso c también muestra una disminución en la incidencia conforme se aumenta.

Para observar únicamente el cómo los alumnos argumentaron sus respuestas se consideró una categorización de esquemas de argumentación propuesta por Flores y sus colegas (Flores, 2007; Flores, Gómez y Flores, 2010), la cual está basada en los estudios de Harel y Sowder (Harel, 2008; Harel y Sowder, 1998). Así se puede definir como práctica argumentativa al "conjunto de acciones y razonamientos que un individuo pone en juego para justificar o explicar un resultado o para validar una conjetura nacida durante el proceso de resolución de un problema" (Flores, 2007, pág. 71) y a partir de ello categorizar las respuestas de las personas en los siguientes tipos de esquemas:

• Autoritarios, donde sus argumentaciones se apoyan en las afirmaciones hechas por una autoridad (profesor, libro de texto).
• Simbólicos, donde se utiliza un lenguaje matemático y símbolos de manera superflua y poco consistente sin llegar realmente a las conclusiones deseadas, el sujeto puede mencionar conceptos poco claros o inventados.
• Fácticos, en los que se hace un recuento de lo que se hizo o se repiten hechos evidentes de una situación a manera de explicación o justificación de algún resultado, como una serie de pasos que parecen un algoritmo.
• Empíricos, en los cuales el apoyo está en hechos particulares (inductivos) o en un dibujo (perceptuales), donde este constituye un argumento por sí mismo y no un apoyo para visualizar el argumento.
• Analíticos, donde se sigue una cadena deductiva, sin que por ello se llegue forzosamente a una conclusión válida.

Debido a la naturaleza del instrumento aplicado en el análisis se encontraron justificaciones que no estaban total o mayormente caracterizadas en un único esquema entre los de tipo autoritario, simbólico y fáctico, por lo que se tuvo necesidad de proponer una categoría que incluye características de estos esquemas y que se denominó esquema fáctico-simbólico. En concreto este se refiere cuando el alumno utilizó lenguaje matemático superfluo y además hizo un recuento de hechos evidentes para explicar o justificar su resultado.

Se observó que los alumnos tienden a utilizar el recuento de pasos realizados, mayormente acompañados de operaciones para justificar sus resultados. Recurren a casos particulares para ejemplificar cómo elevar una potencia y con frecuencia el uso del lenguaje matemático es inventado o débil (recurren al uso de términos deícticos), en el sentido de no nombrar adecuadamente los objetos matemáticos. El siguiente gráfico 2 muestra los resultados generales.

Gráfico 2. Porcentajes de categorías de esquemas de argumentación identificados para el reactivo 1

Para el caso del esquema autoritario, aunque son pocas las evidencias encontradas (el 4.28%), muestran que los alumnos usan "lo dicho por su maestro", "por las leyes de los exponentes" o "por los teoremas" como irrefutable, probablemente por una creencia arraigada, respeto al conocimiento del profesor o a lo establecido en los libros. Si el avance al razonamiento deductivo es gradual, todavía alumnos del tercer año recurren a este tipo de "enunciados" para justificar la validez de sus respuestas.

Ejemplo de respuesta en el esquema autoritario (Nm-5-039).

El esquema simbólico, y el empleo de expresiones como "lo de adentro", "lo de afuera", "el número antecesor de la letra", "el número superior", etcétera, podrían ser clasificados como términos deícticos. Esto términos, de acuerdo con Knipping (2008), son usados generalmente en las afirmaciones de los alumnos, tanto como sea posible, cuando reconstruyen la argumentación. La utilización de tales expresiones es mayormente realizada por los jóvenes de segundo y tercer año, concluyendo que no se logró desarrollar las competencias que en la Educación Secundaria se plantean para Matemáticas, específicamente la de comunicar información matemática (Secretaría de Educación Pública [SEP], 2011, pág. 23).

Ejemplo de una respuesta en el esquema simbólico (Nm-5-016)

La presencia del esquema fáctico es el que tiene un porcentaje mayor (34%) y evidencia el hecho de que los alumnos recurren a desarrollar la operación solicitada, es decir, hacen un recuento y describen el proceso, a veces auxiliados con flechas. Para darle más solidez a sus respuestas algunos describen casos particulares cómo resolver "un número elevado a la tres", o bien a la forma generalizada de escribir una potencia. De esta forma se evidencian algunas indicaciones de que puede aparecer el esquema empírico (inductivo), lo cual se comentará más adelante.

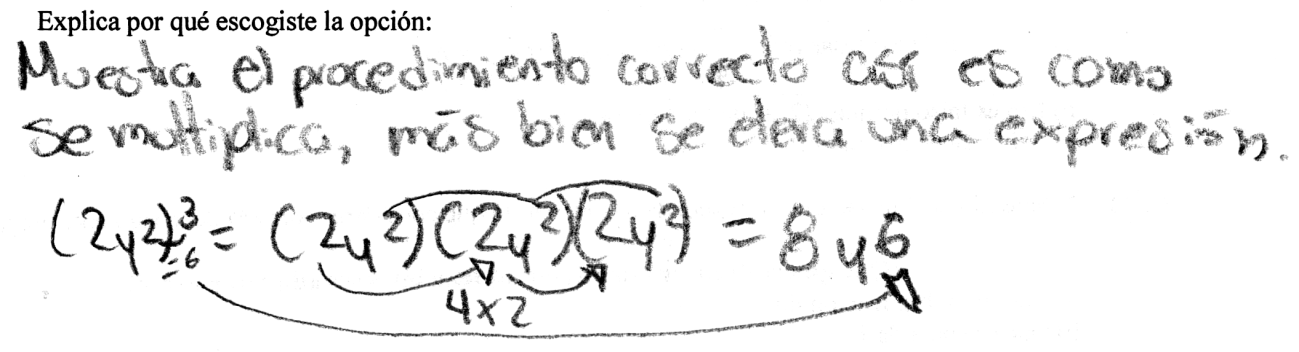
Ejemplo de respuesta en el esquema fáctico (Sv-2-001)

Por otro lado, el 15.54% de los alumnos empleó el esquema fáctico-simbólico para sus justificaciones, haciendo una mezcla de términos inventados en el relato de su forma de operar y en ocasiones se equivocan en la resolución (ver Ilustración 6). Es importante mencionar que esta categoría tendrá que ser estudiada en investigaciones posteriores.

Ejemplo de respuesta del esquema fáctico-simbólico (Sv-4-015)

El siguiente reactivo analizado para este caso fue el reactivo 2 mencionado en la sección anterior. En este caso los alumnos no sólo tenían que determinar dónde colocar el punto correspondiente a a2 (dado un punto que representaba a un número a), sino justificar por qué escogieron dicha posición.

Al igual que en el reactivo anterior se consideraron las formas de justificar a partir de la categorización de esquemas recién presentada. Esto se ve reflejado en el siguiente gráfico:

Esquemas utilizados por los alumnos para justificar las respuestas del reactivo 2.

(Los casos sin respuesta o con información insuficiente representan el 21% y no se incluyen)

Se puede ver que la mayoría optó por el esquema "autoritario-simbólico", donde no está explícito el uso de símbolos, pero tampoco el uso de un soporte autoritario externo. Por ejemplo:

Ejemplo de justificación considerada como parte de un esquema "autoritario-simbólico" (Sm-4-014)

Podría llamar la atención que la segunda mayor preferencia, después de la categoría recién mencionada, es la que incluye el uso de casos particulares para justificar. No hay procesos deductivos, sino que, como dice Chazan (1993), no son las demostraciones o las deducciones las que convencen a los alumnos, sino los ejemplos:

Ejemplos de justificaciones correspondientes a esquemas empíricos inductivos (Nm-5-013 y Sv-4-032, respectivamente)

La preferencia sobre este tipo de esquemas y la poca proporción de apariciones del esquema analítico lleva a pensar la necesidad de reforzar una idea de las justificaciones en Álgebra que esté más orientada a la generalización.

 

CONCLUSIONES

Es común que en las instituciones se tenga acceso a información cuantitativa sobre algunos aspectos académicos de los alumnos, pero ante el interés de obtener información orientada a la toma de decisiones sobre estrategias en la enseñanza de las matemáticas de este estudio se ha podido considerar que hay procesos más complejos que se mezclan con otros y aumentan las dificultades para el profesor. Tal es el caso de las justificaciones y los esquemas de argumentación que se mencionaron en las secciones anteriores, donde se puede comenzar a dilucidar una jerarquía en su uso. No obstante, con los alumnos participantes se evidenció que el uso de ciertos esquemas de argumentación avanzados no implica que las soluciones sean correctas. Es decir, alguien puede argumentar incluso de manera deductiva y sin embargo obtener las conclusiones no deseadas (incorrectas), que no sean pertinentes o que simplemente no observen lo que se quiere en el proceso educativo.

Nuevamente podemos insistir en considerar el sentido que le otorgan los alumnos a los procesos y los conceptos, pues el énfasis de la demostración matemática en el aula no está en su estructura sino en su sentido y significado.

Además, se esperaría que el "progreso" de los alumnos en la argumentación y las justificaciones fuese gradual para encaminarse al razonamiento deductivo, con el consiguiente abandono de esquemas de argumentación como el autoritario, el simbólico y el fáctico. Todo ello por el énfasis en el uso de la argumentación desde niveles básicos, trascendiendo a los niveles medio y superior.

Sin embargo, los resultados evidencian que aún hay dificultades en semestres avanzados del bachillerato, con el uso reiterado de los esquemas autoritarios y simbólicos para sostener la validez de su resultado. También es notable que alrededor de una quinta parte de los alumnos dejó respuestas en blanco, o bien no proporcionaron información suficiente o fuera de contexto como para poder realizar un análisis.

Así pues, la información obtenida puede dar pie a nuevas investigaciones que generen y difundan conocimientos educativos sobre el aprendizaje delas matemáticas, considerando los retos que implican las demandas sociales, políticas, científicas, culturales y económicas. Todo ello con la finalidad de establecer las bases para proponer estrategias de cambio en los procesos educativos (capacitación docente, cambios curriculares, etcétera) que integren procesos matemáticos de investigación, desarrollo y validación del conocimiento como para de una unidad metodológica-científica.

 

REFERENCIAS BIBLIOGRÁFICAS

Arellano, C. (2013). La argumentación de alumnos de bachillerato al resolver problemas matemáticos. Tesis de maestría inédita. Querétaro: Universidad Autónoma de Querétaro. Recuperado el 17 de diciembre de 2017 de http://ri.uaq.mx/bitstream/123456789/1388/1/RI000656.pdf

Avilés, A. (2014). El pensamiento reflexivo como marco para el aprendizaje de la Geometría Euclidiana en un sistema por competencias. Tesis de maestría inédita. Querétaro: Universidad Autónoma de Querétaro. Recuperado el 17 de diciembre de 2017 de http://ri.uaq.mx/xmlui/bitstream/handle/123456789/1803/RI001416.pdf

Bloch, E. D. (2000). Proof and fundamentals. Boston, EEUU: Birkhäuser.

Bourbaki, N. (1972). Elementos de historia de las matemáticas. Madrid, España: Alianza Universidad.

Chazan, D. (1993). High school geometry students' justification for their views of empirical evidence and mathematical proof. Educational Studies in Mathematics, 24 (4), 359-388. Recuperado el 17 de diciembre de 2017 de https://www.researchgate.net/profile/Daniel_Chazan/publication /226499841_High_school_geometry_students'_justification_for_their_views_of_empirical_evidence_and_mathematical_proof/links/56940f9908ae425c68962e3d.pdf

Flores, Á. H. (2007). Prácticas argumentativas y esquemas de argumentación en profesores de matemáticas del bachillerato. Tesis doctoral inédita. Ciudad México: Cinvestav. Recuperado el 17 de diciembre de 2017 de http://ri.uaq.mx/xmlui/bitstream/handle/123456789/1803/RI001416.pdf

Flores, C., Gómez, A., & Flores, Á. H. (2010). Esquemas de argumentación en actividades de geometría dinámica. Acta Scientiae, 12 (2), 22-42. Recuperado el 17 de diciembre de 2017 de http://www.periodicos.ulbra.br/index.php/acta/article/download/33/30

Harel, G. (2008). Students' proof schemes revisited. En P. Boero (Ed.), Theorems in school (pp. 65-78). Rotterdam, Holanda: Sense Publishers.

Harel, G., & Sowder, L. (1998). Students' proof schemes: Results from exploratory studies. En A. Schoenfeld, J. Kaput, & E. Dubinsky (Edits.), Research in collegiate mathematics education III (pp. 234-282). EEUU: AMS. Recuperado el 17 de diciembre de 2017 de http://www.math.ucsd.edu/~harel/publications/Downloadable/Students%27%20Proof%20Schemes.pdf

Knipping, C. (2008). A method for revealing structures of argumentations in classroom proving processes. ZDM The International Journal on Mathematics Education, 40 (3), 427-441.

Larrazolo, N., Backhoff, E., & Tirado, F. (2013). Habilidades de razonamiento matemático de estudiantes de educación media superior en México. Revista Mexicana de Investigación Educativa, 18 (59), 1137-1163. Recuperado el 17 de diciembre de 2017 de http://www.redalyc.org/pdf/140/14028945006.pdf

 

 

Recibido: enero de 2018.
Aprobado: febrero de 2018.

 

 

El autor se desempeña como profesor e investigador en la Jefatura de Investigación y Posgrado de la Facultad de Ingeniería de la Universidad Autónoma de Querétaro, México, particularmente en el área de Didáctica de las Matemáticas.