Introducción
La educación matemática, en un contexto escolar y universitario, se ha situado en un terreno llano y diverso, donde la investigación adquiere fuerza y fundamentos para el desarrollo y el posicionamiento de la enseñanza y el aprendizaje. Tal es el impacto que ha adquirido la educación matemática, que las evaluaciones internacionales (TIMSS, PISA, entre otras) tienen fuertemente incorporado en sus instrumentos la matemática escolar y el desarrollo del aprendizaje de ella. Desde esta perspectiva, se hace fundamental que la investigación en este campo se lleve a cabo en todos los niveles educativos, así como que esté dirigida a mejorar el aprendizaje de los estudiantes a través del diseño de estrategias que faciliten al docente el tránsito entre aquello que se desea enseñar y lo que se pretende que el estudiante aprenda.
Dada la relevancia de la educación matemática, es perentorio fortalecer el currículum de la asignatura de matemática, evaluando y reformulando sus contenidos. En este contexto, hay ciertos temas o tópicos matemáticos que no son puestos en un relieve lo suficientemente robusto en el currículum escolar, pero que tienen gran importancia como objeto matemático de aprendizaje, por la diversa cantidad de conceptos que involucran. Un ejemplo de ello, son los contenidos exhibidos por el plan diferenciado de matemática de tercero medio propuesto por el Ministerio de Educación de Chile (MINEDUC), el cual no recibe actualización desde el año 2005 y por consiguiente ha sufrido de un envejecimiento curricular, puesto que solo existe un marco curricular que lo sustenta. En dicho plan, se expone la unidad de “Lugares Geométricos” (MINEDUC, 2005), el cual incluye la noción de distancia en el plano cartesiano, la circunferencia y parábola como lugar geométrico.
En el contexto de este fragmento de la matemática, Astorga & Parraguez (2014) señalan que la problemática evidenciada es que “no se comprenden las secciones cónicas en distintos modos de pensar, ni aisladas de la métrica usual”, por el contrario, se precisa de métricas no usuales para avanzar en la comprensión de estos objetos. En la dirección en que se orientó la indagación presentada, esto es una problemática, que consideró como objeto matemático las cónicas, pero inserta en la unidad “Lugares Geométricos”, por la gran versatilidad que tiene en sus representaciones y por articular diversos conceptos geométricos y algebraicos presentes en los contenidos curriculares de la enseñanza secundaria, y porque esta unidad además de poseer características propias, logra sintetizar y reforzar contenidos que le preceden.
Considerando la problemática enunciada y su carácter cognitivo, se estableció como objetivo de investigación diseñar una secuencia de actividades didácticas que permita el tránsito entre los distintos modos de pensar las cónicas, articulados por métricas no usuales, para que las representaciones gráficas de ellas no sean concebidas como definiciones y se adoptó el marco teórico de la didáctica de la matemática denominado Modos de Pensamiento de Anna Sierpinska (2000), cuyo foco principal está centrado en el objeto matemático, mostrando “las diferentes formas de comprender ese objeto, para alcanzar un nivel de abstracción superior” (Parraguez 2012, p. 74), a través de interacciones entre el pensamiento práctico y teórico, en pro de alcanzar la comprensión de las cónicas.
Métodos
Desde la necesidad de comprender e interpretar fenómenos sociales “al tratar de comprender la realidad circundante en su carácter específico” (González, 2003, p.133), es que la presente investigación se circunscribe en un enfoque cualitativo y está amparada en el paradigma interpretativo-comprensivo, pues busca comprender, desde una realidad específica, el porqué de la problemática en estudio para proponer respuestas y mejoras de la misma.
Los instrumentos utilizados para la medición inicial y propuesta de actividades didácticas, fueron cuestionarios de respuestas abiertas, aplicados a dos casos de estudio (Stake, 2010), conformados por 17 estudiantes de tercero (caso 1) y 15 de cuarto medio (caso 2) respectivamente (últimos años de secundaria en Chile), de la asignatura del plan diferenciado “álgebra y modelos analíticos”, de dos realidades educativas distintas. Para la construcción de la propuesta de actividades didácticas, se consideraron las especificaciones contenidas en la Figura 1, donde se detallan actividades de acercamiento a las tres métricas propuestas y actividades respecto a las cónicas en distintas métricas. Luego del diseño, la propuesta en su totalidad fue validada por 10 estudiantes universitarios de primer año (caso 3) y 5 profesores del sistema escolar (caso 4). La propuesta validada fue aplicada a los estudiantes secundarios (casos 1 y 2) de quienes este artículo reportará sus resultados.
La propuesta consta de seis ítems de actividades (Figura 1). Los ítems 1, 2 y 3 corresponden al trabajo con las métricas, donde cada ítem está compuesto por tres actividades. Los ítems 4, 5 (tres actividades cada uno) y 6 (dos actividades) corresponden a las cónicas.
Los resultados que se presentarán en este artículo corresponden al segmento de la propuesta que mejor representa al trabajo de los aprendices con las métricas no euclidianas. La propuesta tiene dos versiones equivalentes en el uso de la métrica, para cada cónica. A continuación, la Figura 2 muestra los ítems 4, 5 y 6 de la propuesta en la versión “norma 1” para la circunferencia.
Resultados y discusión
La teoría de los Modos de Pensamiento de Anna Sierpinska
La investigadora Anna Sierpinska (2000) a través de su trabajo en el álgebra lineal, afirma que los y las estudiantes comprenden los objetos matemáticos del álgebra lineal de forma más práctica que teórica. Esto último detona una serie de investigaciones, con base en las cuales Sierpinska construye la teoría de los Modos de Pensamiento, con la finalidad de lograr la superación de dos posiciones dogmáticas opuestas evidenciadas, Parraguez (2012), la primera que rechaza los números dentro de la geometría (pensamiento práctico) y la otra que objeta que la intuición geométrica pueda pensarse desde un campo propiamente aritmético (pensamiento teórico).
El resultado de esta superación, logra dar mayor nivel de abstracción, a los conceptos propios del álgebra lineal, transitando desde modos de pensamiento prácticos hacia teóricos. La articulación de los pensamientos teórico y práctico, facilita la comprensión del objeto matemático en estudio, por lo que este marco teórico propicia el trabajo con problemáticas de naturaleza cognitiva, donde la comprensión del objeto matemático juega un rol protagónico. La articulación de los tipos de pensamiento (teórico y práctica) conlleva la unión de modos de pensar asociados, evidenciando su potencial cuando están en interacción, esto indica que “son igualmente útiles, cada uno en su propio contexto, y para propósitos específicos” (Parraguez 2012, p. 9).
De la interacción de estos tipos de pensamiento práctico y teórico, se desprenden los siguientes modos de comprender un objeto matemático:
Modo sintético-geométrico (SG): Modo desde el pensamiento práctico, el cual describe el objeto en su forma, desde la representación gráfica convencional, utilizando elementos de la geometría como puntos, líneas, curvas, planos, por mencionar algunos. “Habitualmente este modo se presenta natural e inicialmente, dado que basta con considerar una representación geométrica básica para abordar este modo. Es fácil de conseguir además en estudiantes de enseñanza escolar básica” (Astorga, 2015, p. 19).
Modo analítico-aritmético (AA): Modo adscrito al pensamiento teórico, utiliza el álgebra para describir el objeto a través de fórmulas, relaciones numéricas o ecuaciones. Para lograr la comprensión a través de este modo, “es necesario que el estudiante cuente con herramientas algebraicas, que le permitan desprenderse del pensamiento práctico y transite hacia el teórico, por lo que es alcanzable, según el desarrollo del pensamiento, en estudiantes de enseñanza media inicial” (Astorga, 2015, p. 20).
Modo analítico-estructural (AE): Modo de pensamiento teórico, que utiliza la axiomática, propiedades o invariantes para describir al objeto. “Este modo de pensar, es posible de conseguir en estudiantes de enseñanza secundaria, pues ya existe el álgebra en su formación, lo cual propicia el pensamiento abstracto, potenciado desde lo teórico” (Astorga, 2015, p. 20).
Aunque epistemológicamente este marco teórico se enfoca en el álgebra lineal, es posible extender su uso a otros tópicos de la matemática que puedan confrontar ambos tipos de pensamiento (práctico y teórico). Importante es que, al lograr el tránsito entre los tres modos de pensar SG, AA y AE, se logra la comprensión profunda del objeto matemático tratado (Sierpinska, 2000).
Construcción de las cónicas a través de la teoría de los Modos de Pensamiento
Las secciones cónicas, por sus características algebraicas y geométricas, son un contenido apropiado para ser tratado desde el encuadre teórico de los modos de pensamiento, que precisan de la forma práctica (SG) y teóricas (AA - AE) para describirlas.
Desde la perspectiva de la teoría de los modos de pensamiento, las secciones cónicas se describen (Astorga & Parraguez, 2014) a través de los tres modos siguientes:
SG-cónicas: Las secciones cónicas comprendidas desde la figura plana o como la intersección de un plano con un cono.
AA-cónicas: Comprendidas como las ecuaciones cartesianas que las definen.
AE-cónicas: Comprendidas como el lugar geométrico de todos los puntos del plano que cumplen con características dadas y definidas.
Es importante destacar que desde la construcción epistemológica del objeto matemático “cónicas”, también se evidencian los modos de pensarlas, pues en la época antes de Cristo, con Menelao, Euclides y Apolonio, se aprecia la construcción de las cónicas a través de relaciones entre segmentos, curvas, superficies y planos, lo cual las adscribe al modo SG. Luego Pappus (Siglo IV D. C), logra dar con una definición como lugar geométrico en el plano, intencionando de esta forma el modo AE, y finalizando, la introducción de la geometría analítica con Descartes y Fermat (silgo XVII) manifiesta el modo de pensar AA (Astorga, 2015).
Construcción de las cónicas a través de la teoría de los Modos de Pensamiento usando métricas no euclidianas
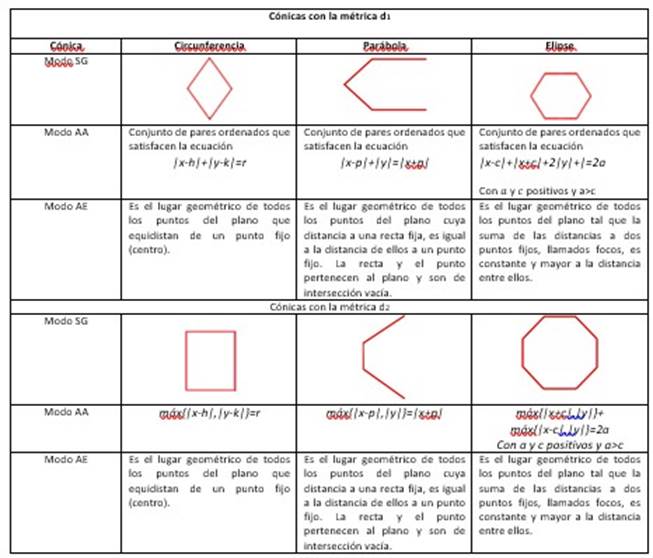
El problema evidenciado en Astorga & Parraguez (2014), manifiesta que la métrica usual es un impedimento para desprender a las cónicas de su forma y fortalecer la comprensión desde la definición. Por ello, se proponen dos métricas no euclidianas “d1: norma 1” y “d2: norma infinita” (además de la euclidiana), cuyos modos de pensar las cónicas en estas métricas se describen y presentan en la Figura 3. (Astorga & Rojas, 2009)
Con la finalidad que los aprendices de enseñanza secundaria alcancen la comprensión de las cónicas con base en un lugar geométrico que las describa y en concordancia con el marco teórico propuesto, se diseñó una propuesta de actividades didácticas a través de una secuencia de enseñanza para el aprendizaje de las cónicas. El currículum escolar chileno no incorpora el tratamiento de la hipérbola, por lo que esta investigación consideró como cónicas a la circunferencia, parábola y elipse. La propuesta busca como objetivo propiciar el tránsito entre los distintos modos de pensar las cónicas, articulados por la métrica usual y métricas no euclidianas: etiquetadas como “norma 1” y “norma infinita”.
Para una breve descripción matemática de las dos métricas, considérense los puntos A(x1, y1) y B(x2, y2), entonces se define la métrica “norma 1” entre los puntos A y B como d1(A,B) = |x2-x1|+|y2-y1| y “norma infinito” como d2(A,B)=máx{|x2-x1|,|y2-y1|}.
Casos de Estudio
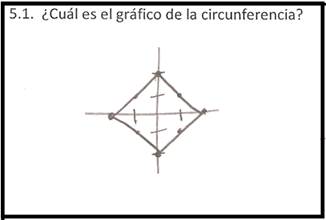
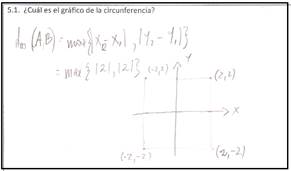
Los resultados son múltiples, pero para ejemplificar se mostrarán los resultados obtenidos en los casos 1 y 2, detallándose aquellos asociados a la circunferencia desde las métricas no euclidianas, en coherencia con el. Figura 2, que es un ejemplo de la propuesta para una cónica en particular, no obstante, las conclusiones son generales.
Con respecto a las métricas no euclidianas
Los estudiantes del caso 1 en la métrica “norma 1”, no lograron realizar el tránsito entre los tres modos de pensar las cónicas, dado que para transitar desde el SG-cónicas al AE-cónicas y viceversa, se requiere de la ecuación que otorga el modo AA-cónicas y desde donde, analíticamente se puede obtener la gráfica de cada cónica. Esto se explica porque la forma de cada cónica, está adiestrada por la métrica euclidiana -en el sentido que es usualmente trabajada en situaciones de aula-. Los estudiantes del caso 2 tampoco lograron realizar el tránsito descrito utilizando la “norma infinita”, dado que también requerían del modo AA-cónicas, sin embargo, lograron transitar desde el modo AA-cónicas al SG-cónicas, Figura 4, articulando los pensamientos práctico y teórico, y por ende mostrando evidencias del aprendizaje del objeto tratado.
En el caso 2 con la métrica “norma 1”, los estudiantes lograron el tránsito secuencial entre los modos AE-cónicas - AA-cónicas - SG-cónicas, en la cual se aprecia el tránsito desde el modo AA-cónicas hacia el SG-cónicas, ambos desde el AE-cónicas. En este caso puntual, la secuencia finaliza con el modo SG-cónicas, que describe la forma de las curvas desconocidas para ellos, y que logran determinar gracias a un trabajo previo en la ecuación que representa la cónica, a través de la definición como lugar geométrico en función de la métrica utilizada.
En la métrica “norma Infinito” ocurre lo mismo para los estudiantes del caso 1, con la salvedad de que puede en ocasiones identificar el tránsito desde el modo AA-cónicas hacia el AE-cónicas. En la Figura 5 se ilustra esto último, usando de ejemplo la circunferencia.
En el caso 2, existen evidencias que muestran el tránsito entre los modos AA-cónicas de posición inicial y el modo SG-cónicas al lograr la gráfica, determinando que las ecuaciones presentadas correspondían a circunferencias en distintas métricas, transitando hacia el modo AE, donde la invariante es la definición de circunferencia y por lo tanto es ello lo que tienen en común, Figura 6, mostrando la coexistencia y articulación entre los pensamientos prácticos y teóricos.
Desde las métricas para cada cónica y los casos de estudio
En el caso 1: respecto a la métrica, se determinó que en general (71%) comprende que existen distintas formas de medir trayectorias, todo dependerá del contexto definido. El 85% de los estudiantes, analizaron la métrica euclidiana a través de los modos de pensamiento. Esto se manifestó en el tránsito desde el modo SG-cónicas al AA-cónicas y desde ambos al AE-cónicas. Finalmente, el análisis de la norma 1 (d1), generó dos secuencias de tránsito entre modos. El primer tránsito se logró desde el modo AA-cónicas hacia el AE-cónicas (y viceversa) y desde el modo AA hacia el SG, considerando algunos elementos del modo AA como articuladores de ese tránsito.
Respecto a las cónicas, la circunferencia bajo la métrica euclidiana, logró mostrar tres secuencias de tránsito distintas. Se logró evidenciar la secuencia SG - AA y viceversa. Curiosamente, cuando se involucró a la norma 1 (d1) en la circunferencia, se propició la secuencia AA - SG - AE, la cual prosperó y se evidenció en diversos informantes. Esto muestra que la circunferencia logra diversos tránsitos entre los modos de pensar, afianzando la comprensión misma del objeto Cónicas.
En la parábola con la métrica euclidiana, se evidenció la secuencia AE - AA - SG. Luego al involucrar a la métrica norma 1 (d1), se generaron dos secuencias entre unos informantes. La primera AA - SG y la segunda (más completa) AE - AA (Viceversa), desde AA hacia SG y desde SG hacia AE (Viceversa). Esto muestra que los tres modos fueron articulados actuando la métrica. Otros informantes manifestaron las secuencias AE - AA - SG y AA - SG - AE.
Para la elipse, fue menos fructífero el tránsito entre los modos de pensar, dado que tanto para la métrica euclidiana como para la norma 1 (d1), solo se evidenció el tránsito AA - SG
En el caso 2: respecto a la métrica norma Infinito d2, la secuencia de las cónicas SG - AA - AE, muestra que en el análisis de la métrica en los modos de pensar hubo comprensión de los estudiantes. El posicionamiento se generó fuertemente en el modo AA-cónicas, al realizar el análisis de la métrica d2 a través de los modos de pensar. Esto da cuenta de que esta métrica, a diferencia de la norma 1, no logró variados tránsitos entre los distintos modos, pero sí logró evidenciar tránsito y permanencia entre los pensamientos práctico y teórico, lo que muestra comprensión de la nueva métrica utilizada (d2).
Respecto a las cónicas en la métrica d2, la circunferencia fue claramente mejor tratada por el caso 2, coincidiendo con las secuencias de tránsito que generó el caso 1 para la circunferencia en la métrica euclidiana, no así con la métrica d2, pues solo se consiguió el tránsito SG - AA. Si bien no muestra variados posicionamientos ni tránsitos entre distintos modos, si logran el tránsito entre los tipos de pensamiento práctico (SG) y teórico (AA), evidenciado que los informantes de este caso 2, comprendan la circunferencia en sus modos de pensarla.
Para la parábola, al igual que en la circunferencia, los posicionamientos y tránsitos son pocos, pero se consiguió posicionamiento en el modo AA y el tránsito entre AA - SG, lo que da cuenta del tránsito entre los pensamientos teórico y práctico, evidenciando comprensión de la parábola en la métrica norma infinita(d2).
Respecto a la elipse, los tránsitos aun cuando son escasos en esta métrica d2, muestran fortaleza en el pensamiento teórico, posicionándose en el modo AA y desde ahí el tránsito hacia el modo SG, situado en el pensamiento práctico, lo cual evidencia comprensión de la elipse en la métrica norma infinito (d2).
Conclusiones
Desde el referente teórico y las métricas norma 1 y norma infinito
Para el aprendizaje integral del objeto matemático en estudio, se requiere del tránsito entre los distintos modos de pensar las cónicas. Como resultado de esta investigación queda de manifiesto que la métrica “para el objeto matemático cónicas” actúa como articuladora entre los distintos modos de pensarlas y además, es la que quiebra el paradigma de la definición de cónicas a través de la imagen que las representa y por lo tanto, logra guiar a los aprendices hacia la comprensión de las cónicas con base en el lugar geométrico, logrando una construcción integral de las cónicas y por lo tanto, generando aprendizaje en los estudiantes.
La propuesta de actividades didácticas logró su propósito fuertemente con la métrica norma 1 (d1), al generar diversas secuencias de tránsito entre los modos de pensar. Esto asiente un nivel de comprensión profundo de las cónicas articuladas por esta métrica, dado el tránsito bidireccional entre los pensamientos práctico y teórico.
Respecto a la métrica infinito (d2), se puede concluir que, aun cuando generó escasos tránsitos entre los modos de pensar las cónicas (en comparación con la métrica (d1), estos tránsitos adquieren fuerte significación dada la mayor dificultad que esta métrica requiere para el trabajo con las cónicas. Además, estos tránsitos son entre los tipos de pensamiento, es decir, entre lo teórico y práctico, evidenciado comprensión de las cónicas en esta métrica.
Las evidencias presentadas muestran que los tipos de pensamiento coexisten en el tratamiento de las cónicas con métricas no usuales d1 y d2, evidenciado diversos tránsitos entre los modos de pensar (SG, AA y AE) y por lo tanto, logrando comprensión profunda (integral) de las cónicas.