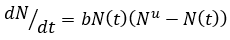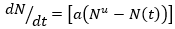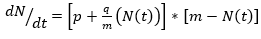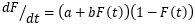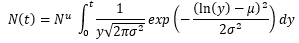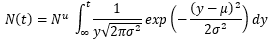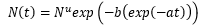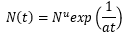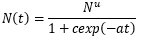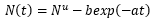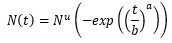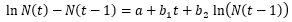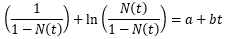Introducción
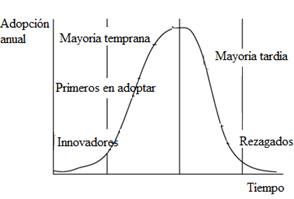
El proceso de difusión de un producto tecnológico es una práctica a través de la cual un producto se comunica mediante ciertos canales a lo largo del tiempo entre los integrantes de una estructura social. Se han utilizado diferentes modelos de difusión, especialmente después de los años sesentas del pasado siglo, para capturar la tendencia de difusión en forma de ecuaciones y patrones matemáticos (Meade & Islam, 2006, 2010). Estos modelos se han aplicado para estudiar diversos procesos de difusión que incluyen la población de automóviles, televisión, computadoras, bienes de consumo, etc., así como la frecuencia de auges económicos, el número de accidentes automovilísticos mortales, el desarrollo de la industria de la informática y el número de muertes por VIH (Fisher & Pry, 1988; Meade & Islam, 1998; Peres, Muller & Mahajan, 2010; Rogers & Shoemaker, 1971); (Baynes, 2009). La difusión también se ve como un proceso de cinco etapas - la conciencia, el interés, la evaluación, el juicio y la adopción (Rogers & Shoemaker, 1971). Estas corresponden a las diferentes etapas de adopción de los consumidores durante el desarrollo del mercado, clasificadas como innovadores, primeros adoptantes, mayoría temprana, tardía y rezagada; según el momento de la adopción, ya que la tecnología se introduce en el mercado (figura 1).
Estos factores que facilitan o dificultan la difusión y conducen el proceso están interrelacionados haciendo la difusión un fenómeno complejo (Chung & Kim, 2017). Las tasas de difusión son específicas del contexto, dependiendo de factores socioeconómicos, tecnológicos e institucionales (Choi, Wong, Chang & Park, 2016).
Sin embargo, existe incertidumbre con respecto a la extensión y el tiempo para la difusión de un producto tecnológico. Por citar algún ejemplo, la reacción de fisión nuclear es una invención que se utilizó por primera vez en un reactor para producir energía comercial que generó la quinta parte de la electricidad en los Estados Unidos de América después de cuatro décadas.
La presente contribución tiene como intención evidenciar la estructura matemática de los patrones y las variables que caracterizan y predicen el comportamiento, en el mercado, de diversos productos tecnológicos. Para logra este popito se desarrolla una investigación bibliográfica en enfocada dentro de los límites del directorio académico Scopus.
Desarrollo
Como métodos investigativos en el desarrollo de este artículo, se inició realizando un proceso de acopio de investigaciones socializadas solo en idioma ingles y dentro de las fronteras del catálogo o directorio académico Scopus, en los últimos 40 años. Estas delimitaciones se enfocaron al criterio de búsqueda models of diffusion of technological to the market.
Un segundo momento fue la selección de los trabajos, cuestionado esta vez, el índice de citas con que contaban estos. Para lograr esta meta, se empleó el software de análisis bibliométrica Publish or Perish 2017. Con esta herramienta se pudo precisar que las publicaciones citadas en este documento contaras con un índice de citas igual a 7 o superior a este valor.
Sinopsis bibliométrica de las investigaciones y desarrollo de modelos matemáticos en el proceso de difusión de productos tecnológicos
De 1974 a la actualidad se registran 360 contribuciones en del directorio Scopus. Bajo el cierto de búsqueda models of diffusion of technological to the market. En la figura 2 se puede observar el desempeño de la comunidad científica en las últimas décadas, en torno a la temática tratada. La line discontinua y de color rojo, marca una clara tendencia al incremento de las contribuciones científicas en este sentido.
La comunidad científica internacional muestra un creciente interés por estas prácticas dado que facilita y predice con gran certidumbre la conducta de diversos productos tecnológicos de cara a las exigencias de un mercado con cada vez más criterio de juicio, complejo y dinámico. Este mercado está sustentado por un conglomerado de patrones socio económicos interrelacionados.
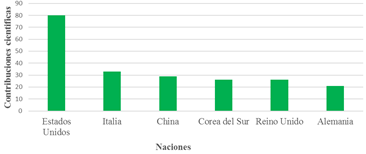
Evidentemente las naciones que hoy día llevan las riendas del destino económico global, son las naciones que mayores contribuciones científicas en esta línea investigativa exponen. La figura 3 corrobora la anterior afirmación, reflejando los seis países a la cabeza en estas investigaciones.
Los modelos matemáticos en el proceso de difusión de productos tecnológicos, en el mercado
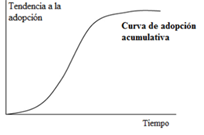
Se ha demostrado que los procesos de difusión en general siguen una curva S. Ver figura 4. Existen diversos ejemplos para representar este patrón en forma de S en la evolución natural de muchos fenómenos en la sociedad, como por ejemplo la difusión inicial de los monasterios en el continente Europa hace ya más de varios siglos, así como el nacimiento y auge de la producción de energía eléctrica (Grübler, 1996).
Los procesos de difusión de productos tecnología de modelado se derivaron inicialmente de la teoría del crecimiento de una colonia de células biológicas en un medio. Dado que el crecimiento de una célula estaría limitado debido a nutrientes o espacio limitado, se ralentizaría y se saturaría dando como resultado un patrón de curva S. De manera similar, los modelos de difusión de productos tecnológicos suponen que el crecimiento de una tecnología o una innovación depende del total de los adoptantes potenciales y la tasa de aumento se representa por la ecuación 1 de difusión fundamental denominada modelo de difusión de la influencia interna.
Donde:
N (t) |
es la adopción acumulativa en el tiempo t |
Nu |
es el potencial final |
b |
es el coeficiente de difusión |
La ecuación 1 representa básicamente una curva de crecimiento logístico y se utiliza directamente en la difusión de productos tecnológicos, lo que supone que el proceso de difusión es influenciado por los adoptantes anteriores. Si la influencia sobre la difusión es externa, la ecuación para el modelo de influencia externa viene dada por la ecuación 2 como:
Donde:
N (t) |
es la adopción acumulativa en el tiempo t |
Nu |
es el potencial final |
a |
es el coeficiente de difusión |
Un modelo de influencia mixta que combina las ecuaciones anteriores (1) y (2) fue presentado por primera vez por Bass para representar el primer crecimiento de compra de un nuevo producto duradero en marketing (Bass, 2004). El modelo Bass es un modelo de influencia mixta con tres parámetros p, q y m; p representa el coeficiente de innovación (a, en la ecuación anterior) y q es el coeficiente de imitación (b en la ecuación anterior = q / m) y m es el potencial total. El modelo de difusión de Bass está dado por la ecuación 3:
Mahajan & Peterson (1985), clasifican los modelos de difusión de la siguiente manera:
Modelos de difusión fundamentales (interna, externa e influencia mixta): estos modelos suponen básicamente que el proceso de difusión es binario, hay un potencial total distinto y constante, los coeficientes son constantes en el tiempo, etc.
Modelos de difusión flexible: los supuestos siguen siendo similares a los modelos de difusión fundamentales, pero son relativamente flexibles con respecto al punto de inflexión donde la tasa de difusión es máxima o simetría con respecto al punto de inflexión.
Refinos y extensiones: muchos de los supuestos fueron modificados para desarrollar modelos de difusión mejorados o revisados que se sub-clasifican en:
Modelos de difusión dinámica: se considera el máximo potencial técnico como dinámico y no estático,
Modelos de difusión de innovación múltiple: la innovación se considera no completamente independiente de todas las demás innovaciones, sino independiente en un sentido funcional y son complementarias, contingentes y sustitutivas de otras innovaciones,
Modelos de difusión espacial y temporal que supusieron principalmente que el crecimiento en el número de adopciones en cada región variaría y que el número relativo de adopciones sería mayor en aquellas regiones más cercanas a las regiones de origen de la innovación,
Modelos de difusión multi-etapa que consideran la adopción como un proceso multi-etapa y no binaria
Los modelos de adopción múltiple captan las compras.
Por último, los modelos de difusión con agentes influenciadores / cambiantes, que consideran la difusión no sólo como una función del tiempo, sino también como coeficientes en función de los parámetros específicos de la tecnología.
La tabla 1 A. 1 proporciona ejemplos de las categorías y aplicaciones de modelos matemáticos de difusión, anteriormente mencionados. (Mahajan & Peterson, 1985). La publicación de Meade and Islam (2006) clasifica los modelos de difusión como:
Un intento de racionalización de diferentes modelos de difusión el trabajo de los autores Jain, Rai, Sharma & Bhargava (1991), indica que la mayoría de las ecuaciones de difusión se reducen a dos momentos. El primer momento se representa en la forma G (1-F) en función de los adoptantes potenciales y absorbe los términos restantes en A (f) que es un factor de conversión y determina cuántos de los posibles adoptantes pueden convertirse; F representa la fracción de adoptantes en cualquier momento dado 0≤A(F)≤1 y 0≤G (1-F) ≤1 ( tabla 3 A. 3).
Hay varias revisiones notables de los enfoques de modelado de difusión (Baptista, 2000; Mahajan & Peterson, 1985; Meade & Islam, 1998, 2006; Rao & Kishore, 2010). Estas investigaciones muestran el rico y creciente conocimiento de la investigación teórica y empírica en el proceso de difusión de nuevos productos, servicios y tecnologías. En tales revisiones se cubren el avance y las mejoras de los modelos. En la contribución desarrollada por los investigadores Robinson and Lakhani (1975), introdujeron variables de marketing en la parametrización de los modelos y examinaron políticas de precios óptimas asociadas con la difusión de nuevos productos. Como los procesos de difusión están influenciados por muchas variables de decisión, se desarrolló un Modelo Generalizado de Bass (MGB). Los autores Norton and Bass (1987), intentaron la difusión de sucesivas generaciones de tecnología y los investigadores Gatignon, Eliashberg & Robertson (1989), generalizaron los modelos para considerar innovaciones en diferentes etapas de difusión en varias naciones del mundo. En todos los modelos de difusión, la estimación de parámetros y su interpretación es medular para la evaluación o cuantificación de la influencia del proceso de difusión de un producto tecnológico. Varios procedimientos de estimación son también analizados y criticados en la literatura y en el contexto del modelo de difusión, generalmente son un problema de tipo no lineal. Por lo tanto, la mayoría de los intentos de estimación de parámetros son transformaciones lineales seguidas por Métodos Mínimos Cuadrados (MMC). Algunas de las técnicas sugeridas para las estimaciones de parámetros incluyen, además de los MMC, la Estimación Algebraica (EA), estimación de mínimos cuadrados no lineal y máxima verosimilitud. La contribución (Meade & Islam, 2010) sostienen que las comparaciones empíricas han recibido menos atención. La elección de los modelos de difusión y los métodos de estimación de los parámetros son específicos de sus aplicaciones para situaciones y requisitos particulares. Es importante que la selección del modelo esté guiada por formas apropiadas de parámetros que depender de cualquier expresión matemática que se ajuste a los datos que se analizan.
Aplicaciones de modelos matemáticos del proceso de difusión en el mercado de productos tecnológicos
Existen numerosos ejemplos en la literatura sobre el uso de modelos de difusión para diversas aplicaciones. L trabajo de Mahajan & Peterson (1985), destaca los tres usos típicos y aplicaciones normativas, descriptivas y de predicción de los modelos de difusión. Esta contribución destaca el uso de nuevos modelos de difusión de productos y también se ilustran muchos pre lanzamiento, lanzamiento y post lanzamiento de nuevas decisiones estratégicas de productos. Por ejemplo, decidir sobre el momento de introducción de un nuevo producto en el mercado y la incertidumbre en cuanto a su rendimiento con respecto a la fijación de precios / publicidad. Entre los modelos de difusión, el modelo Bass ha sido ampliamente utilizado para diversos tipos de análisis de difusión. El artículo de Bass (2004), declara que ha existido cientos de aplicaciones del propio modelo Bass. Una breve revisión de las aplicaciones de los modelos de difusión muestra ( tabla 4 A. 4) que las aplicaciones distribuyen en tres tipos:
el estudio de la difusión general de la nueva tecnología o la innovación
examinar la fijación de precios como una variable de difusión y
propósitos de pronóstico - demanda, etc.
La ( tabla 4 A. 4) destaca algunos ejemplos de aplicación específica de modelos de difusión seleccionados. Como se puede ver, los modelos de difusión se han aplicado extensamente en bienes de consumo comerciales.
Limitaciones de la investigación: en el desarrollo de este artículo se consideran contribuciones científicas proyectadas solo en idioma inglés y contenido en el catálogo académico investigativo Scopus. El periodo de búsqueda abarca desde la década de los setenta a la actualidad. Los artículos referenciados en esta publicación se consideraron por tener un índice de citas de 7 en adelante.
Conclusiones
El proceso de difusión en el mercado, de un producto tecnológico determinado, es una práctica a través de la cual un producto se comunica mediante ciertos canales a lo largo del tiempo entre los integrantes de una estructura social. Se han utilizado diferentes modelos de difusión, especialmente después de los años sesentas del pasado siglo, para capturar la tendencia de difusión en forma de ecuaciones y patrones matemáticos.
Los modelos matemáticos de difusión de productos representan un instrumento útil para comprender el comportamiento y el desempeño de productos o tecnologías en el mercado. Aunque la difusión de tecnologías o productos no sigue un patrón uniforme único y es un fenómeno complejo, los modelos matemáticos se han utilizado para explicar las tasas de difusión y estimar mediante análisis predictivos, los parámetros o coeficientes de las ecuaciones del modelo de difusión. Las aplicaciones de los modelos de difusión se han limitado principalmente a productos comerciales con pocos o ningún vínculo con las políticas gubernamentales.
La comunidad científica internacional muestra un creciente interés por estas prácticas dado que facilita y predice con alto grado de certidumbre el comportamiento de diversos productos tecnológicos, de cara a las exigencias de un mercado cada vez más exigente y complejo, el cual está sustentado por un conglomerado de patrones socio económico conexo.