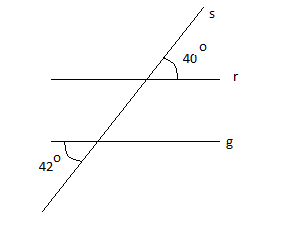Introducción
La necesidad de elevar la calidad de la enseñanza de la Matemática ha estado presente en la comunidad internacional de educadores matemáticos desde la segunda mitad del pasado siglo XX, necesidad que emana, no solo, de las exigencias del desarrollo científico - técnico, sino también, de las exigencias del proceso formativo del estudiante en el cual la matemática desempeña un importante rol, pues la formación matemática es de hecho un componente esencial de la formación multilateral del hombre en cualquier sociedad.
Al analizar, por un lado, los retos de la enseñanza de las ciencias en el nuevo milenio y, por otro lado, los cambios metodológicos aconsejables a raíz del análisis de las tendencias internacionales en la enseñanza de la Matemática, es posible comprender la actualidad y la vigencia del Decálogo de Didáctica de la Matemática Media del educador matemático español, Puig Adam- citado por Kilpatrick, et al. (1994), que fue además miembro fundador de la Comisión Internacional para el Estudio y el Mejoramiento de la Enseñanza de la Matemática (CIEAEM).
Sobre la base de estos postulados y de las exigencias de la enseñanza de las ciencias en el nuevo milenio, es posible comprender la actualidad y vigencia de este decálogo que, trasciende en el tiempo, en el contexto de las transformaciones que tienen lugar en la enseñanza de las ciencias, en particular de la Matemática. Este decálogo, continua nuevo, pues, como dijera Freire (2010), “lo viejo que preserva su validez o que encarna una tradición o marca una presencia en el tiempo continua nuevo”. (p.32)
Las normas o sugerencias didácticas contenidas en este decálogo, constituyen una referencia obligada para todos los educadores matemáticos en el actual siglo XXI. Hacer realidad estas sugerencias didácticas - como las calificó el propio autor- es una forma, no solo, de dar respuesta a los cambios radicales y revolucionarios que necesita la enseñanza de la Matemática en los momentos actuales, sino también, a las exigencias de la UNESCO en relación con la enseñanza de las ciencias en el nuevo milenio. Es objetivo de este trabajo analizar cada una de estas sugerencias y la forma de concretarlas en las prácticas educativas actuales, lo cual contribuye, sin lugar a dudas, a la formación didáctica de las nuevas generaciones de profesores de matemática.
Desarrollo
Para iniciar, y sin pretender hacer una biografía del maestro Pedro Puig Adam, es importante señalar que fue un excelente educador matemático español que vivió entre 1900 y 1960. Dedicó toda su vida a la enseñanza de la Matemática y a la formación de profesores de matemática para la enseñanza media, fue profesor de Metodología de la Enseñanza de la Matemática. Sus concepciones acerca de la matemática y de su enseñanza están plasmadas en su extensa obra que consta de una veintena de libros y más de un centenar de artículos y trabajos de investigación (Kilpatrick, et al., 1994).
De particular interés para los educadores matemáticos de todas las latitudes del planeta son su peculiar manera de enseñar matemáticas, según cuentan sus alumnos, así como las reflexiones acerca de cómo enseñar matemática, las que están claramente reflejadas en su clásico Decálogo de la Didáctica de la Matemática Media. Puig Adam (1955)- citado por Kilpatrick, et al., 1994.
En este decálogo, sintetizó sus ideas sobre la Didáctica de las Matemáticas, en tal sentido expresó:
Se me piden normas didácticas. Preferiría despertar una conciencia didáctica: sugerir formas de sentir antes que modo de hacer. Sin embargo, por si valieran, ahí van las sugerencias que estimo más fundamentales:
No adoptar una didáctica rígida, sino amoldada en cada caso al alumno, observándolo constantemente.
No olvidar el origen concreto de la Matemática ni los procesos históricos de su evolución.
Presentar la Matemática como una unidad en relación con la vida natural y social.
Graduar cuidadosamente los planos de abstracción.
Enseñar guiando la actividad creadora y descubridora del alumno.
Estimular dicha actividad despertando el interés directo y funcional hacia el objeto del conocimiento.
Promover en todo lo posible la autocorrección.
Conseguir cierta maestría en las soluciones antes de automatizarlas.
Cuidar que la expresión del alumno sea traducción fiel de su pensamiento.
Procurar a todo alumno éxitos que eviten su desaliento. (Kilpatrick, et al., 1994, p. 137)
En lo que respecta a la primera sugerencia: no adoptar una didáctica rígida, sino amoldada en cada caso al alumno, observándolo constantemente, el maestro Puig Adam, se refería al carácter flexible de la didáctica, que no es otra cosa que diferenciar la enseñanza de acuerdo a las particularidades individuales de los alumnos. Se sabe que no todos los alumnos aprenden de la misma forma y que sus estrategias y estilos de aprendizaje no son los mismos, lo cual exige que el proceso de enseñanza - aprendizaje tenga un carácter diferenciado sobre la base de del nivel de preparación y desarrollo de los alumnos.
El profesor debe tener conciencia que cada alumno debe cumplir los elevados requerimientos de la enseñanza uniforme plasmados en los programas y planes de estudio (currículo), pero también, que la enseñanza debe potenciar al máximo las potencialidades individuales de cada alumno en aquellos aspectos en los cuales su personalidad se halla fuertemente comprometida (Arteaga, et al., 2016).
Una didáctica amoldada al alumno exige, por un lado, un diagnóstico certero y profundo, no solo de los conocimientos que posee el alumno, sino también, del nivel de desarrollo psíquico alcanzado, sobre todo de aquellos recursos personológicos que le permiten aprender, entre otras, las capacidades de razonamiento y de generalización, por otro lado, de una valoración sistemática de ese nivel de preparación y desarrollo.
Ambos aspectos constituyen exigencias del proceso de enseñanza - aprendizaje en la escuela cubana: diagnóstico de la preparación y desarrollo del alumno (Rico & Silvestre, 2003). De especial interés en ese diagnóstico es la valoración de su nivel de preparación y desarrollo. Este problema exige reflexionar en tres aspectos importantes y que han sido menos trabajados desde el punto de vista didáctico, el primero, ¿cuál debe ser el contenido de esa valoración en la enseñanza de las matemáticas? ¿Qué valorar desde el punto de vista del contenido y desde el punto de vista del desarrollo de la personalidad del alumno? La otra cuestión es ¿qué tareas, instrumentos y técnicas hay que utilizar para hacer esa valoración?
Como se puede apreciar la evaluación se desplaza de una calificación o puntuación hacia una valoración, que implica hacer un análisis descriptivo y valorativo del nivel alcanzado por el alumno en cada etapa del aprendizaje en las asignaturas de ciencia.
Es importante aclarar que especificar el contenido de la valoración es un proceso complejo, pues el proceso de valoración debe abarcar la personalidad del alumno como un todo, al mismo tiempo, el modo en que se especifica el contenido afecta tanto a los instrumentos a utilizar (métodos y técnicas), como a sus resultados.
Los aspectos de carácter específico que deben ser objeto de valoración como parte de la enseñanza de las matemáticas, deben ser debatidos y precisados por los profesores, los que, a su vez, diseñarán los instrumentos a utilizar. En ambos casos es imprescindible considerar cuatro aspectos importantes:
Diseño de los instrumentos a utilizar.
Respuesta que dan los alumnos.
Análisis de las respuestas.
Interpretación de los resultados.
No se trata de valorar solamente si la respuesta es correcta o no, de lo que se trata es comprender el razonamiento del alumno. Una actividad cuyo resultado no es el esperado puede brindar informaciones útiles que a veces no se tienen en cuenta.
Por ejemplo, digamos que a un alumno de 7mo grado se le propone la tarea siguiente:
Observa la fig. 1 y responde:
¿Qué relación existe entre las rectas r y g? Fundamenta
Se pueden encontrar alumnos que respondan que las rectas r y g son paralelas, mientras que otros alumnos responderán que las rectas r y g no son paralelas porque los ángulos alternos determinados por la secante s y las rectas r y g no tienen la misma amplitud.
Es obvio que los alumnos que plantean que las rectas son paralelas, están situados en el primer nivel de la capacidad de razonamiento geométrico, según los Van Hiele (1957)-citado por Gooding (2011); y Ricaldi (2014). Es decir, en el nivel visual o de reconocimiento, mientras que los alumnos que plantean que las rectas no son paralelas y lo fundamentan correctamente están ubicados en el nivel deductivo lógico - formal, es decir tienen un mayor nivel de desarrollo de la capacidad de razonamiento geométrico.
En la valoración tiene un valor importante la interpretación de la respuesta que dan los alumnos ante una situación determinada.
Es importante aclarar que amoldar la didáctica al alumno no significa adaptarse al alumno, sino adecuar el sistema de influencias con el objetivo de desarrollar al máximo sus capacidades.
En cuanto a la segunda sugerencia: no olvidar el origen concreto de la Matemática ni los procesos históricos de su evolución. Esta sugerencia es el mejor antídoto didáctico para erradicar las visiones erróneas de la ciencia que se transmiten y que se observan con mucha frecuencia en la enseñanza de las matemáticas en nuestras escuelas (Fernández, et al., 2005), en particular la descontextualizada, la aproblemática y la ahistórica.
Esta afirmación está en consonancia con la visión que Puig Adam tenía de la Matemática, según él los conceptos matemáticos se transmiten desprovistos de cualquier significación real y esa era la causa del divorcio entre la matemática y la realidad (Kilpatrick, et al.,1994). Esto por supuesto es también una de las causas de la matofobia- terror a las matemáticas- que comienza a manifestarse desde que el niño entra a la escuela y se acentúa en la medida en que va avanzando en los estudios, sobre todo en los niveles medio y medio superior hasta el punto en que muchos alumnos al terminar el bachillerato (preuniversitario) deciden optar por carreras universitarias en las que no tengan Matemática en su plan de estudio.
Para Puig Adam, si la escuela quiere proporcionar al educando una formación matemática completa que lo prepare para utilizar en su vida práctica y profesional esos conocimientos, la enseñanza de la matemática en todos los niveles educacionales no debe descuidar, el sentido de aplicación en su doble aspecto de abstracción y concreción. Los conceptos matemáticos tienen su origen en la realidad cotidiana y a ellos se llegan mediante abstracciones, que son a su vez el resultado de observaciones, de experiencias e intuiciones que se realizan desde los primeros grados de la escuela.
Esto exige, por una parte, incorporar la historia de la matemática a la enseñanza y, por otra parte, diseñar y/o elaborar alternativas didácticas para la enseñanza de esta ciencia que tengan en cuenta el origen de esos conocimientos, lo que a su vez requiere de una elevada preparación de los profesores en cuestiones relacionadas con la historia, la epistemología y la filosofía de la matemática, algo que en ocasiones está ausente de los currículos para la formación de profesores de estas asignaturas.
En una de las tendencias generales actuales en la enseñanza de la matemática De Guzmán (2007), resalta que para comprender la interacción dialéctica entre la realidad y la matemática es necesario acudir, por una parte, a la propia historia de la matemática, que devela ese proceso de emergencia de nuestra matemática en el tiempo, y, por otra parte, a las aplicaciones de la matemática, que hacen patentes la fecundidad y potencia de esta ciencia.
Al referirse a los cambios metodológicos aconsejables, De Guzmán (2007), habla sobre la utilización de la historia en la educación matemática, para él la historia se puede y se debe utilizar, entre otras cosas, para entender y hacer comprender una idea difícil del modo más adecuado.
En el perfeccionamiento que se realiza actualmente en el sistema educacional cubano, en particular en la nueva generación de planes de estudio de matemática, se incluyen aspectos de carácter histórico en los libros de texto. Ahora es necesario exigir a los profesores que hagan un buen uso de ellos.
La tercera sugerencia: presentar la Matemática como una unidad en relación con la vida natural y social, está estrechamente relacionada con la anterior.
De Guzmán (2007), refiere que nexiste consenso en el hecho que el aprendizaje de las matemáticas no se realice explorando las construcciones matemáticas en sí mismas, en las diferentes formas en que han cristalizado a lo largo de los siglos, sino apoyándose constantemente en las variadas situaciones del mundo real que les dieron y les siguen dando su motivación y vitalidad.
En el 8vo. Congreso Internacional de Educación Matemática ICME-8, efectuado en Sevilla en 1996, D`Ambrosio (1996), expresó: “Las matemáticas son una cosa que se encuentran en todas las culturas,…. Toda la naturaleza está repleta de formas y figuras matemáticas…Todo el universo responde a algún conocimiento matemático. Entonces yo me pregunto ¿por qué sólo se hacen matemáticas a partir de lo que se ve en los libros? ¿Por qué no hacer matemáticas mirando hacia el entorno?”
Si a estas reflexiones de D`Ambrosio (1996), le añadimos la afirmación realizada en su tiempo por Galileo Galilei cuando dijo que la naturaleza era un libro abierto escrito en lenguaje matemático, entonces podemos comprender que no es recomendable enseñar matemáticas sin tener en cuenta el entorno en el cual el alumno desarrolla su vida. La comunidad con sus construcciones, parques, e instituciones, así como las principales actividades que en ellas tienen lugar, constituyen excelentes materiales de aprendizaje.
Una de las tendencias internacionales actuales en la enseñanza de la matemática, identificadas por De Guzmán (2007), es el continuo apoyo en la intuición directa de lo concreto. Apoyo permanente en lo real. Para ello el mencionado autor señala que:
Es necesario cuidar y cultivar la intuición en general, la manipulación operativa del espacio y de los mismos símbolos.
Si la matemática es una ciencia que participa mucho más de lo que hasta ahora se pensaba del carácter de empírica, sobre todo en su invención, que es mucho más interesante que su construcción formal, es necesario que la inmersión en ella se realice teniendo en cuenta mucho más intensamente la experiencia y la manipulación de los objetos de los que surge.
Nuestra enseñanza ideal debería tratar de reflejar este carácter profundamente humano de la matemática, ganando con ello en asequibilidad, dinamismo, interés y atractivo.
Un ejemplo que permite enseñar matemáticas a partir de su relación con la vida, lo constituyen las máquinas “Fregat” que se utilizan para el regadío en las plantaciones de las empresas de cultivos varios, las cuales describen un círculo, lo que permite calcular el área que abarca en función del radio “brazo de la Fregat” o determinar que longitud debe tener el brazo para regar una superficie determinada.
En fin, no se puede enseñar matemáticas al margen de su relación con la naturaleza y con la vida social de los educandos. Esto no solo permite una mejor comprensión de los contenidos matemáticos, sino de cómo la matemática está presente en su quehacer cotidiano.
No es menos cierto que los alumnos se preguntan constantemente ¿para qué necesito de las matemáticas? No hay que esperar que tengan ante sí una situación que exija de la utilización de las matemáticas. La escuela debe prepararlos para la vida y debe hacerles conciencia de que la matemática- como dijera C. Silva- es un instrumento indispensable para conocer el mundo y es necesario empezar por el conocimiento de ese micromundo que es la comunidad en la cual desarrolla su vida y en la cual están presentes las matemáticas.
Cómo analizar e interpretar los datos que aparecen en la prensa y en otras publicaciones de la llamada prensa plana, sin conocimientos básicos de Estadística.
Es necesario hacer de la comunidad, de los asentamientos poblacionales, etc., aulas especializadas de matemática. El mejor y más valioso recurso didáctico para enseñar y aprender matemáticas en la escuela está al alcance de todos los niños, adolescentes y jóvenes: el entorno que los rodea.
Por esta razón, el maestro o profesor al planificar una unidad didáctica o una clase debe, primero que todo, mirar hacia afuera y preguntarse: ¿en qué lugares del entorno? o ¿en qué actividades que realizan los miembros de la comunidad, incluidos los alumnos, están presentes las matemáticas?
La cuarta sugerencia: graduar cuidadosamente los planos de abstracción, es una consecuencia de la primera y responde, por un lado, a una idea que expresó Comenio-citado por Labarrere (1988)- en su Didáctica Magna: “Enseñe todo conforme a la capacidad, que aumenta con la edad y adelanto en los estudios”. Esta es la esencia del principio de la asequibilidad de la enseñanza y, por otro lado, las exigencias del contenido a asimilar que en ocasiones requiere de un alto grado de abstracción por parte de los alumnos.
En la enseñanza de la Matemática, en los primeros años de la escuela, es decir, en la educación primaria o básica como se le denomina en algunos países, deben predominar los métodos inductivos para la obtención de los conocimientos, los que se combinarán con los métodos deductivos la final de este tipo de enseñanza cuando ya se haya alcanzado un mayor nivel de desarrollo del pensamiento lógico - deductivo del alumno. Aunque los métodos deductivos predominan en la enseñanza media o media superior, nunca se debe renunciar a su utilización combinada, tanto en la fase de obtención o construcción de los conocimientos objetos de asimilación, como en la fase de fijación de los conocimientos.
Un mismo problema puede resolverse, en algunos momentos de la enseñanza, utilizando reflexiones lógicas del contenido y en otro utilizando procedimientos sistemáticos, por ejemplo:
A un alumno de secundaria básica se le puede pedir que resuelva ecuaciones exponenciales por reflexiones lógicas del contenido, sin tener que introducir el concepto ecuaciones exponenciales, es decir, utilizando las propiedades de las potencias y ya en la educación preuniversitaria o bachillerato se le puede introducir el concepto y el procedimiento para resolver ecuaciones exponenciales.
En la educación primaria los conceptos deben formarse utilizando métodos sustitutos para la definición de conceptos, tales como: la comparación, la distinción, la ejemplificación, la descripción, la caracterización, la conjugación de la descripción y la caracterización (Guétmanova, et al., 1991), los que serán sustituidos posteriormente por las definiciones formales, que es el último nivel en el desarrollo de la capacidad para definir (Jungk, 1983).
La quinta recomendación: enseñar guiando la actividad creadora y descubridora del alumno. En el análisis de los principios metodológicos aconsejables, De Guzmán (2007), insiste en la necesidad de estimular en el alumno la búsqueda independiente, el descubrimiento paulatino de estructuras matemáticas sencillas, de problemas interesantes relacionados con tales situaciones que surgen de modo natural, finalmente reconoce que, la búsqueda con guía, sin aniquilar el placer de descubrir, es un objetivo alcanzable en la enseñanza y aprendizaje de las matemáticas.
Coincidimos con De Guzmán (2007), cuando plantea que una enseñanza concebida de esta forma resulta llena de sentido, plenamente motivada, que constituye una verdadera fuente de satisfacción y placer intelectual, de asombro ante el hecho de descubrir un nuevo conocimiento, lo que a su vez puede fomentar el gusto y el interés de los alumnos hacia la matemática.
Enseñar guiando la actividad creadora o descubridora de los alumnos supone, en primer lugar, un cambio en el rol tradicional del maestro o profesor como transmisor de conocimientos ya acabados, y, en segundo lugar, reconceptualizar las situaciones de enseñanza - aprendizaje, prestando especial atención al tipo de tareas que tiene que se le pueden plantear a los alumnos durante el aprendizaje, y enseñar estrategias de búsqueda y de descubrimiento.
Es necesario que la actividad del estudiante comience con el análisis de situaciones problemáticas que le permitan identificar y definir el problema que se espera que resuelva, que consiste como es lógico, en la necesidad de elaborar (buscar o descubrir) un nuevo conocimiento (concepto, regla, algoritmo, proposición, etc.). A esto le siguen tareas dirigidas a la búsqueda de ese conocimiento (Armada, et al., 2016).
De hecho, encontrar un nuevo conocimiento puede generar plena satisfacción en el alumno. El análisis del nuevo conocimiento puede contribuir a identificar un nuevo problema a resolver. En la sexta sugerencia, que tiene que ver con la anterior: estimular dicha actividad despertando el interés directo y funcional hacia el objeto del conocimiento, Puig Adam se refería a la motivación para dicha actividad, reconociendo el rol que desempeña la motivación para propiciar el descubrimiento o la creación.
En este sentido es necesario puntualizar algo a lo que ya nos hemos referidos en otros trabajos, y es la concepción de situaciones problemáticas que reflejen en la mayor medida posible los interese, aspiraciones y necesidades de los alumnos.
Para lograr que los alumnos se motiven por el estudio de un determinado tema en la matemática, las situaciones problemáticas deben elaborarse en estrecha relación con el entorno que rodea a los educandos (contexto), que expresen o en las que estén reflejadas sus principales actividades cotidianas, por ejemplo, para que los escolares, interesados en la práctica de un deporte se interesen por el estudio de los sistemas de ecuaciones lineales, es necesario que las situaciones problemáticas se elaboren tomando en cuenta el deporte que practican o del que son fanáticos.
El alumno tiene que saber qué utilidad tienen los contenidos objeto de asimilación, no solo para su vida cotidiana, sino también, para su futura actividad laboral o profesional.
Las aplicaciones la matemática a la vida y a otras ciencias, no solo, satisfacen, sino que despiertan los intereses del alumno por el estudio de la matemática (Claxton, 1994; Camarena, 2017).
Para ello se requiere un estudio profundo del entorno y del contexto que rodea al estudiante y de la comunidad en que viven, para conocer, en primer lugar, las actividades que realizan o prefieren, en segundo lugar, los conocimientos matemáticos empíricos que utilizan, las particularidades de la comunidad en que viven y que pueden ser utilizadas para la enseñanza y el aprendizaje de la Matemática. Una fábrica, un parque, un supermercado pueden y de hecho deben convertirse en un espacio para aprender Matemática (Vasco, 1994; D´Ambrosio, 1996; Arteaga, et al., 2016).
De particular importancia para concretar esta sugerencia en el proceso de enseñanza - aprendizaje de la Matemática, lo constituyen los principios y las claves para contextualizar la enseñanza de la Matemática, propuestos por Parra (2013), así como, las fuentes de contextos para la contextualización y los niveles cognitivos de los eventos contextualizados, propuestos por Camarena (2017), en su teoría educativa de la matemática en el contexto de las ciencias.
Los principios propuestos por Parra (2013), se enmarcan en los principios de lo que se denomina la
Educación matemática realista Freudenthal, citado por Parra (2013). Al respecto el mencionado autor señala: “Su principal tesis es asumir la matemática como una actividad humana. Desde esta perspectiva enseñar matemática supone establecer una conexión de la matemática escolar con la realidad del estudiante, de manera que éste la vea como una herramienta para organizar, comprender y transformar el mundo que le rodea. Desde el punto de vista epistemológico significa traspasar los procesos de enseñanza de la matemática que actualmente la muestran como una disciplina sustentada en un sistema organizado de manera deductiva, inalcanzable y ya finalmente construida, a una matemática en continua construcción, en el que la interacción de los estudiantes con su entorno sea un proceso de reinvención orientado por el docente”. (pp. 79)
Una de las claves propuestas por Parra (2013), es que el profesor conozca el objeto matemático, sus fundamentos, su historia y sus aplicaciones en diferentes contextos. Esto le permite pensar en situaciones similares que pudieran adaptarse a las situaciones de aprendizaje que se diseñen.
Otra de las claves es saber buscar información y analizarla desde la mirada del aula. Si se quiere conocer los problemas que originaron un determinado tópico matemático o conocer sus aplicaciones actuales, lo que implica una minuciosa búsqueda, utilizando diere fuentes, tales como: Wikipedia u otros recursos, como por ejemplo, Internet.
Por su parte, Camarena (2017), reconoce tres fuentes de contexto para los eventos contextualizados: “las demás ciencias que estudia el alumno, es decir, vinculación entre disciplinas, las actividades profesionales y laborales futuras del alumno, esto es, la articulación entre matemáticas y las necesidades de los distintos ámbitos sociales y las situaciones de la vida cotidiana, es decir, la relación de la matemática con el quehacer diario de todo individuo”. (pp. 7 - 8)
Estas tres fuentes se pueden utilizar, no solo, en la enseñanza media, sino también, en la educación superior, en los diferentes momentos de la clase y en los diferentes tipos de clases. Estas tres fuentes, por su complejidad en la formación previa del alumno, le permitieron a la mencionada autora, establecer tres niveles cognitivos de los eventos contextualizados:
Nivel bajo. Está dado por situaciones de la vida cotidiana, aunque hay situaciones que pueden llegar a un nivel alto. El punto es que esta fuente sí proporciona niveles bajos. Este nivel es idóneo para el nivel educativo básico, también denominado primario en algunos países, sin embargo, se emplea en todos los niveles educativos.
Nivel medio. El nivel medio se localiza en las demás ciencias que cursa el alumno en sus estudios. El nivel educativo en donde se desarrolla frecuentemente este nivel cognitivo es en secundaria y bachillerato, o nivel educativo medio, así como en el nivel universitario.
Nivel alto. Este nivel, también denominado nivel complejo, proporciona contextos de la vida real en el ámbito profesional y laboral. Generalmente son aplicados en los últimos semestres de estudio del alumno, cuando tiene los conocimientos suficientes de matemáticas y de las demás asignaturas para enfrentar exitosamente el tipo de eventos que ofrece esta fuente. (pp. 8)
La contextualización de la enseñanza de la Matemática, le permite al alumno comprender para qué sirven los conocimientos objeto de estudio en esta asignatura, es decir, para qué se utiliza. Es oportuno señalar que existen otras formas de contextualización, no muy generalizadas, como la contextualización con el recurso de la Historia de la Matemática, propuesta por Sánchez (2013), la cual puede insertarse en la segunda sugerencia.
En la séptima sugerencia: promover en todo lo posible la autocorrección, el profesor Puig, se refería a enseñar a los alumnos a corregir sus propios errores, pero se puede añadir algo más, es decir, enseñarlos a autocontrolar el resultado de lo que hacen, algo que hoy en día no se enseñan en nuestras escuelas. El alumno resuelve una tarea de aprendizaje y no tiene la certeza de si el resultado obtenido es correcto o no. Se limita a esperar a que otros lo hagan y comparar entre ellos los resultados, si todos coinciden, lo más probable es que el resultado sea el correcto.
Es necesario que como parte de la enseñanza el docente enseñe a los alumnos cómo controlar el resultado, que puede ser, recurrir a la operación inversa, utilizando otras vías para verificar que se obtiene el mismo resultado, etc.
En la octava sugerencia: conseguir cierta maestría en las soluciones antes de automatizarlas. Esta sugerencia expresa cómo debe transcurrir el proceso de formación y desarrollo de habilidades y competencias en sentido general. Tiene mucho que ver en este aspecto la manera en qué el profesor conciba el proceso de enseñanza - aprendizaje para que se logren formar conocimientos y habilidades (destrezas) sólidos.
Para ello es importante tener en cuenta, no solo la forma en las que se ejecutan las acciones y operaciones durante la ejecución de una determinada tarea, sino también el tipo de tarea que permite asimilar los procedimientos de solución estudiados. A menudo los docentes gustan de que sus alumnos resuelvan muchas tareas del mismo tipo, lo que, por un lado, conduce a una asimilación prematura de los modos o procedimientos de solución, y, por otro lado, obstaculiza la generalización de estos a la solución de nuevas tareas.
La asimilación consciente de un nuevo modo o procedimiento de solución exige, en primer lugar, de que los alumnos conozcan de antemano las acciones y operaciones que él debe ejecutar como parte del procedimiento, así como, los diferentes tipos de tareas que él puede resolver con dicho procedimiento. Para lo primero él debe disponer de una Base orientadora para la Acción (BOA), donde estén representados, en su forma generalizada esas acciones y operaciones, de modo que ante cada tarea particular él pueda elaborar su propia base orientadora, para lo segundo, se requiere de la utilización de una variedad de tareas representativas de esa clase de tareas, diferentes unas de las otras, donde el procedimiento tenga que sufrir cambios, es decir, omitir acciones, para realizar con éxito la tarea o dónde no haya que utilizar el procedimiento estudiado.
La maestría en las soluciones se logra con tareas del mismo tipo, pero sólo después de haber resuelto tareas que permitan generalizar y reducir el procedimiento, cuando las acciones se ejecuten con una participación cada vez menor de la conciencia y con rapidez y seguridad.
Para materializar con éxito esta norma didáctica, me atrevo a ofrecer algunas sugerencias que son fruto de mis estudios sobre la problemática y de ni experiencia de más de 40 años en la docencia:
Identificar utilizando el método teórico - experimental (Talízina, 1988), las acciones y operaciones que es necesario realizar para resolver tareas de una determinada clase.
Elaborar el procedimiento que sirve de base para la realización exitosa de las tareas, velando por su completitud.
Ejemplificar, utilizando varios tipos de tareas, el procedimiento de solución elaborado, cuidando de realizar todas las acciones y operaciones prescritas, sin omitir ninguna por muy sencilla que parezca.
Dejar que los alumnos resuelvan varias tareas guiándose por el procedimiento estudiado, es decir, analizando y ejecutando cada una de las acciones y operaciones. En esta sugerencia desempeña un rol muy importante el lenguaje y el control que realice el profesor de la actividad que está realizando el alumno.
Cuando el alumno haya interiorizado el procedimiento, se deben ofrecer varias tareas del mismo tipo para el procedimiento logre automatizarse, es decir, utilizarse con rapidez y seguridad, sin tener delante el modelo que contiene las acciones y operaciones que forman parte de este.
Cuando las acciones que forman parte del procedimiento se transforman en acciones internas, generalizadas, reducidas y automatizadas, entonces podemos afirmar que se ha logrado esa maestría de la que habla Puig Adam.
Sobre la novena sugerencia: cuidar que la expresión del alumno sea traducción fiel de su pensamiento. El profesor debe prestar especial atención a las ideas que exprese el alumno, aun cuando no utilice adecuadamente el vocabulario técnico de la asignatura, pero sí que exprese correctamente lo que piensa. Esto permite que el profesor pueda valorar la capacidad de razonamiento del alumno, es decir, a qué conclusión llegó y cómo llegó a ella.
Los aciertos y desaciertos en los razonamientos realizados se revelan en la expresión del alumno. Las capacidades de expresión y de comunicación se consideran una parte importante de la capacidad de razonamiento matemático del alumno (Rico & Sierra, 1994).
Es por esta razón que el lenguaje se convierte en portador del razonamiento matemático del alumno. Para ello es importante que el profesor no solo se limite a pedirle al alumno que explicite lo que hizo parta llegar a una determinada conclusión, sino también, que antes de resolver una determinada cuestión matemática explique lo que va a hacer y como lo va a hacer.
En relación con la última norma del decálogo, la última, pero no por ello la menos importante, yo diría que la más importante: procurar a todo alumno éxitos que eviten su desaliento. Esta sugerencia es la clave para evitar que los alumnos rechacen la asignatura.
Esta norma ratifica algo que ya se mencionó anteriormente, el principio de la asequibilidad de la enseñanza, pues cómo han afirmado muchos pedagogos, la enseñanza debe ir de la más fácil a lo difícil, de lo menos complejo a lo más complejo.
Lo anterior exige de la observancia de los niveles de asimilación: familiarización - reproducción- aplicación- creación. Una vez que el alumno haya adquirido el conocimiento esté debe estar en situación de utilizarlo para resolver tareas similares a las utilizadas por el profesor para su ejemplificación (reproducción).
Esta primera reproducción se conoce como reproducción sin variantes, en las que solo se requiere reproducir el conocimiento estudiado. Las tareas deben ser fáciles, que él alumno pueda comprender fácilmente. Por ejemplo, le enseñamos la fórmula para calcular el volumen de un cono y le pedimos al alumno que calcule el volumen de un cono, conocidos su radio y su altura.
La segunda reproducción debe ser con variantes, es decir, donde el alumno tenga que buscar algunos elementos necesarios y que no se le dan en la tarea, por ejemplo: Se les pide a los alumnos calcular el volumen de un cono, pero conocidos el radio y la generatriz, donde él reconozca que debe determinar la longitud de la altura utilizando otro conocimiento para poder resolver la tarea.
Una vez conseguido esto se utilizan tareas para la aplicación del conocimiento a la solución de tareas de la vida o de otras ciencias, por ejemplo: Una pieza de hierro de forma cilíndrica tiene 3, 0 cm de radio y 12 cm de altura. Calcula la masa de la pieza. En este caso el alumno debe reconocer que para calcular la masa de la pieza necesita conocer la densidad del hierro y el volumen de la pieza.
El último nivel de asimilación la creación, en el cual identifico dos subniveles. La reproducción creadora y la creación propiamente dicha, requiere de la utilización de tareas de un mayor grado de complejidad. Es en este nivel donde se utilizan los tres tipos genéricos de tareas que se proponen en mi tesis doctoral para el trabajo independiente creativo de los alumnos, a las cuales ya hicimos referencia anteriormente.
En este nivel son de gran utilidad la utilización de problemas de final abierto y los problemas no rutinarios o problemas no familiares, es decir, problemas a los que él alumno no está acostumbrado, como, por ejemplo:
Hallar un número de cuatro cifras que satisface las condiciones siguientes: la suma de los cuadrados de las dos cifras de los extremos es igual a 13; la suma de los cuadrados de las dos cifras del medio es igual a 85. Si del número buscado se resta 1089, se obtiene un número que se escribe con las mismas cifras, pero en orden inverso.
Conclusiones
Las normas o sugerencias didácticas ofrecidas por Puig Adam en su Decálogo de Didáctica de la Matemática Media, constituyen una buena guía para transformar nuestras prácticas, pues ellas nos dicen qué hacer para contribuir de manera eficaz a la formación matemática de los alumnos, la que necesitan los hombre y mujeres del presente y del futuro para que puedan actuar de forma creadora en la construcción de la sociedad en que viven.
Las sugerencias didácticas ofrecidas por Puig Adam, no son independientes unas de otras. En una misma actividad o tarea matemática se puede observar el cumplimiento de varias.
Este decálogo data de 1955, como ya se dijo, pero preserva su validez en el contexto de las transformaciones que actualmente tiene lugar en la enseñanza de las ciencias en todo el mundo, entre ellas la enseñanza de la Matemática, y esto hace que continúe nuevo como dijera el pedagogo brasileño Pablo Freire, a pesar de que no encarne una tradición, pero si marca una presencia en la época actual.