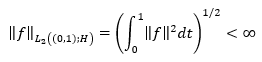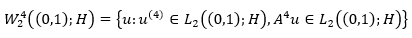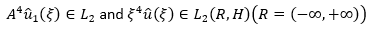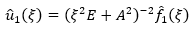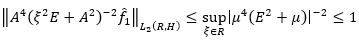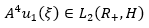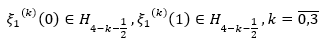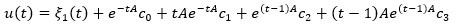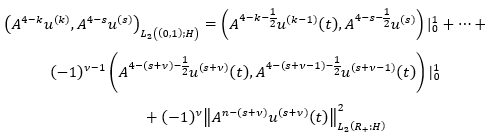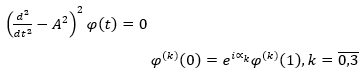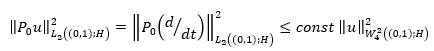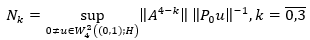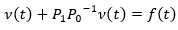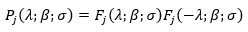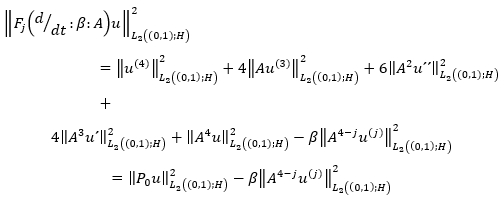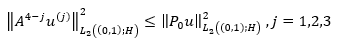Introduction
Many problems in mechanics, mathematical physics, and the theory of partial differential equations lead to the study of the solvability of boundary value problems for operator-differential equations in various spaces (Kreyn & Laptev, 1966; Kreyn, 1967; Yurchuk, 1974; Gasimov & Mirzoev, 1992; Mirzoev & Humbataliev, 2010; Humbataliev, 2014a b, 2020, 2021).
Note that some problems in the theory of elasticity in a strip (Papkovich, 1940, 1941; Ustinov & Yudovich, 1973), problems in the theory of vibrations of mechanical systems (Kostyuchenko & Orazov, 1981), and vibrations of an elastic cylinder (Lyons & Magenes, 1971) lead to the study of the solvability of some boundary value problems for operator-differential equations and the construction of the spectral theory of quadratic beams and high-order beams. For example, the stress-strain state of a slab leads to solving problems of the theory of elasticity in a strip. In the works of Papkovich (1940, 1941; Ustinov & Yudovich (1973); and Orazov, 1979) the boundary value problem of elasticity theory in a strip reduces the solvability of various boundary value problems for a second-order equation and obtained a solution in the form of the limits of decreasing elementary solutions of the homogeneous equation, which is closely related to the double completeness of systems of eigenvectors and associated vectors.
Note that finding the exact values of the norms or their upper bounds for the operators of intermediate derivatives are of independent mathematical interest and have numerous applications in various fields of mathematical analysis (Lyons & Magenes, 1971; Gorbachuk & Gorbachuk, 1984; Mirzoev, 2003), for example, in approximation theory (Stechkin, 1967; Taikov, 1968).
In order to continue let’s define some auxiliary facts and the problem statement. Let H be a separable Hilbert space, and A, a positive definite self-adjoint operator with domain D(A). Let denote by H γ a scale Hilbert space generated by the operator  , and when
, and when  the Hilbert space of vector functions
the Hilbert space of vector functions  , defined in (0,1) almost everywhere with values in H, such as equation 1 is fulfilled.
, defined in (0,1) almost everywhere with values in H, such as equation 1 is fulfilled.
(1)
Further, define a Hilbert space (Lyons & Magenes, 1971) as equation 2 with a norm given in equation 3. Here and in what follows, derivatives are understood in the sense of the theory of distributions.
(2)
(3)
In addition, let’s introduce subspaces space shown in equation 4 where ∝ is a real number. Similarly let’s define  as the set of infinitely differentiable functions with values in H4. As is known (Lyons & Magenes, 1971), the linear space
as the set of infinitely differentiable functions with values in H4. As is known (Lyons & Magenes, 1971), the linear space  is dense everywhere in space
is dense everywhere in space 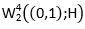 . Then equation 5 follows from the trace theorem being
. Then equation 5 follows from the trace theorem being  dense everywhere in space
dense everywhere in space  .
.
(4)
(5)
In a separable Hilbert space, consider the boundary value problem of equations 6 and 7, where, but  is a linear operator in space.
is a linear operator in space.
(6)
(7)
Definition 1: If for  , which satisfies equation (6) in almost everywhere, then it will be called a regular solution to equation (6).
, which satisfies equation (6) in almost everywhere, then it will be called a regular solution to equation (6).
Definition 2: If for any 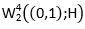 there is a regular solution to equation (6)
there is a regular solution to equation (6)  which satisfies the boundary condition (7) in the sense of the convergence (equation 8) and the inequality (equation 9) then problem (6), (7) is called regularly solvable.
which satisfies the boundary condition (7) in the sense of the convergence (equation 8) and the inequality (equation 9) then problem (6), (7) is called regularly solvable.
(8)
(9)
Then, the objective of this paper is to find sufficient conditions on the coefficients of equation (6), which ensure the regular solvability of problem (6), (7). These conditions are expressed only by the coefficients of equation (6). Note that for equation (6) various boundary value problems in the semiaxis have been investigated by many authors (Kreyn & Laptev, 1966; Ustinov & Yudovich, 1973; Yurchuk, 1974; Gasimov & Mirzoev, 1992; Humbataliev, 2014ab, 2020, 2021).
Development
In a finite domain, the existence and uniqueness of generalized solutions of some boundary value problems were studied by Orazov (1979); and Mirzoev & Humbataliev (2010), in a more general form. In Dubinsky (1973), the existence of periodic solutions to the boundary value problem was investigated, when the main part has the form of equation 10 but the coefficient expressed in equation 11 were complex numbers, and A-self-adjoint operators had a discrete spectrum. Note that for ∝=0 the boundary conditions are periodic, and for ∝=π boundary conditions are antiperiodic. Also when n=1 the periodic problem is covered in the book by Kreyn (1967).
(10)
(11)
First, let's look at the simple problem of equations 12 and 13. Then, we will prove the lemma 1, which we will need in what follows.
(12)
(13)
Lemma 1: At  for any polynomial in the form of equation 14 where
for any polynomial in the form of equation 14 where  the inequality of equation 15 holds, where
the inequality of equation 15 holds, where .
.
(14)
(15)
Proof: Obviously, it suffices to prove (15) for vector functions  equation 16 holds.
equation 16 holds.
(16)
When 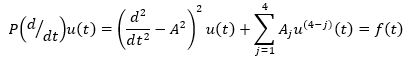 integrating by parts, we obtain equation 17.
integrating by parts, we obtain equation 17.
(17)
As u(t)∈D 0,1 ;H;α , then we get equation 18. Similarly, we find equation 19 for 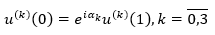
(18)
(19)
In this way we can get equation 20 and the lemma 1 is proved.
(20)
Corollary 1: At  the equality in equation 21 holds.
the equality in equation 21 holds.
Indeed, from the previous expression it's clear that 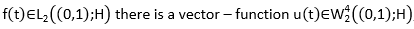 Then, the following theorem takes place.
Then, the following theorem takes place.
Theorem 1: Operator P 0 maps space isomorphically 
Proof: From Corollary 1, it follows that  . Let’s prove that its range of value
. Let’s prove that its range of value  . To this end, let’s prove that problem of equations 12 and 13 has a unique regular solution. For a given
. To this end, let’s prove that problem of equations 12 and 13 has a unique regular solution. For a given  construct a vector function in the form of equation 22 and show that
construct a vector function in the form of equation 22 and show that 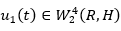 . By Plancherel's theorem, it suffices to prove the conditions of equation 23.
. By Plancherel's theorem, it suffices to prove the conditions of equation 23.
(22)
(23)
It's obvious the relation of equation 24 where f 1 ξ is the Fourier transform of the vector function f 1 t , which is a continuation of the function f t from interval (0,1) on R as a null function. Then equation 25 holds.
(24)
(25)
Since at  we get the relation of equation 26 arriving at equation 27 and similarly
we get the relation of equation 26 arriving at equation 27 and similarly  .
.
(26)
(27)
We denote the narrowing 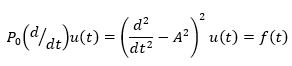 on (0,1) through
on (0,1) through 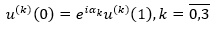 . Then it is obvious that
. Then it is obvious that  and we get the equation 28.
and we get the equation 28.
(28)
Now let´s look for regular solutions problem (12), (13) in the form of equation 29 where  are unknown vectors from space H7/2 (Yurchuk, 1974) and belong to the definition. To define vectors
are unknown vectors from space H7/2 (Yurchuk, 1974) and belong to the definition. To define vectors  we get the following system of equations (equation 30).
we get the following system of equations (equation 30).
(29)
(30)
This system can also be represented in operator form 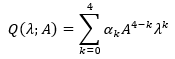 . It's obvious that
. It's obvious that 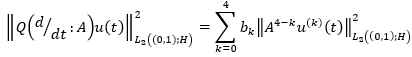 . Let us show that the operator matrix W(A) reversible in space H7/2.
. Let us show that the operator matrix W(A) reversible in space H7/2.
Let 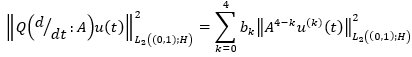 and denote
and denote 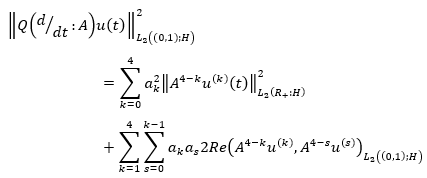 where in the matrix W(A) operator A replaced through
where in the matrix W(A) operator A replaced through 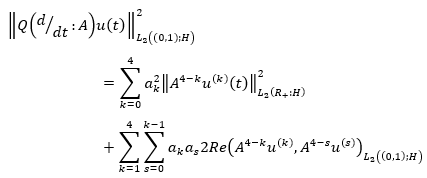 . Obviously, for
. Obviously, for 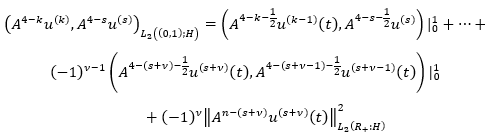 the relation of equation 31 is fulfilled.
the relation of equation 31 is fulfilled.
(31)
(32)
(33
Then the theorem on the inverse operator implies the assertion of Theorem 1. Thus, the expressions in equation 34 are equivalent in space  .
.
(34)
Then it follows from the theorem on intermediate derivatives that the following numbers of equation 35 are finite.
(35)
On the solvability of boundary value problems (6), (7)
Taking the above into account the theorem 2 holds.
Theorem 2: 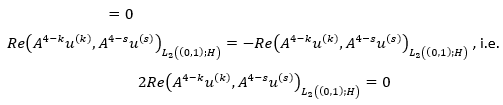 are defined from equality (35), then problem (6), (7) is regularly solvable.
are defined from equality (35), then problem (6), (7) is regularly solvable.
Proof: Let’s write problem (6), (7) in the form of the equation 36 where  Then we obtain the equation 37.
Then we obtain the equation 37.
(36)
(37)
The relation in equation 38 is fulfilled considering that α<1, and we get that, 
(38)
Therefore, equation 39 follows and the theorem is proved.
(39)
Thus, to find the condition for regular solvability, we must find upper bounds for the norms  is a valid parameter.
is a valid parameter.
Lemma 2: Let,  is expressed in the form of equation 40. Then the operator
is expressed in the form of equation 40. Then the operator  is reversible on the imaginary axis and is represented in the form of equation 41 where the beam coefficient may be expressed as equation 42 and every
is reversible on the imaginary axis and is represented in the form of equation 41 where the beam coefficient may be expressed as equation 42 and every  satisfy the relation as can be seen next.
satisfy the relation as can be seen next.
(40)
(41)
(42)
а) 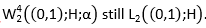 , equation 43.
, equation 43.
(43)
b)  , equation 44.
, equation 44.
(44)
c)  , equation 45.
, equation 45.
(45)
Proof: Let 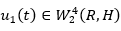 Then it is obvious that for the numerical polynomials of equation 46 i.e., at
Then it is obvious that for the numerical polynomials of equation 46 i.e., at  are on the imaginary axis.
are on the imaginary axis.
(46)
Given that
We get
Corollary 2: With all 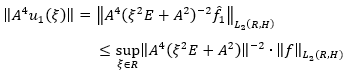 the inequality of equation 50 holds.
the inequality of equation 50 holds.
(50)
Proof: As equation 51 is fulfilled then applying relations (43) - (45) and using Corollary 1, we obtain the relation in equation 52.
(51)
(52)
Theorem 3: With all  Equation 53. We get the relation in equation 54 and the theorem is proved.
Equation 53. We get the relation in equation 54 and the theorem is proved.
(53)
(54)
Then, from Theorems 2 and 3 we obtain the following main theorem
Theorem 4: Let  holds, then problem (6), (7) is regularly solvable.
holds, then problem (6), (7) is regularly solvable.
Conclusions
The theory of partial differential equations lead to the study of the solvability of boundary value problems for operator-differential equations in various spaces. In this work, applying logic, sufficient conditions were found for the solvability of a special type of boundary value problem, which were synthesized in theorem 4. This has special relevance for solving problems in different fields, especially mathematical physics.