Introducción
La teoría del desarrollo cognitivo de Piaget es una teoría integral sobre la naturaleza y el desarrollo de la inteligencia humana desarrollada por primera vez por Jean Piaget. Se la conoce principalmente como teoría de las etapas del desarrollo, pero de hecho, se ocupa de la naturaleza del conocimiento en sí mismo y de cómo los humanos llegan gradualmente a adquirirlo, construirlo y utilizarlo. Además, Piaget afirma la idea de que el desarrollo cognitivo está en el centro del organismo humano y el lenguaje depende del desarrollo cognitivo.
Según Piaget (1981), a los 11 años o más, el niño se encuentra en la fase de Operativo formal. En este período, el niño puede comparar y contrastar alternativas que pueden existir solo en la mente. El mayor desarrollo del lenguaje también hace posible una gama más amplia de interpretaciones. Piaget enfatiza que la característica importante de este período final (que continúa hasta la edad adulta) es la capacidad de manipular los constructos mentales y reconocer las relaciones entre estos constructos. Comprender que un automóvil que viaja quince millas con un galón de gasolina puede viajar ciento cincuenta millas con diez galones de gasolina requiere operaciones formales. Esta es la etapa en la que se enfocará este estudio.
Según Piaget, Matemáticas, y de hecho, la mayoría de los esquemas esenciales no se pueden enseñar, tienen que ser construidos por el niño. En las primeras etapas, la instrucción verbal puede no ser de mucha ayuda. Se deben incluir varios tipos de actividades, que son esenciales para construir esquemas. Al comprender un problema, el niño lo asimila a sus esquemas existentes y lo incorpora a su mundo cognitivo total. Cuando los esquemas existentes son inadecuados para la complejidad del problema, ocurren errores. Entonces el maestro no piagetiano se concentrará en cometer el error. El maestro piagetiano ayudará a crear las condiciones bajo las cuales se creará un nuevo esquema que pueda hacer frente a los nuevos estímulos. Se puede ver que el niño que estudia en un salón de clases tradicional aprende ciertas cosas más rápido por medios mecánicos. Pero el aprendizaje del niño piagetiano será firme y generativo y, por lo tanto, es probable que, a la larga, el niño piagetiano supere al aprendizaje infantil mediante métodos tradicionales (Byrnes, 2020).
A menudo se promueve que las matemáticas otorguen a quienes las estudian una serie de habilidades de pensamiento amplias, tales como: la capacidad de pensar de manera lógica, analítica, crítica y abstracta; tener capacidad para sopesar pruebas con imparcialidad. Esta es una visión de las matemáticas como un suministro de habilidades transferibles que se pueden encontrar en instituciones educativas, gobiernos y corporaciones en todo el mundo. Un material de vista sobre el lugar de las matemáticas en los planes de estudio (Carrillo, et al., 2016).
Las matemáticas y las estadísticas te ayudarán a pensar de manera lógica y clara, y a aplicar una variedad de estrategias de resolución de problemas afirman ciertos autores. Las matemáticas han sido reconocidas durante mucho tiempo como un área de estudio valiosa, incluida la de muchos fuera de las mismas. Algunos autores han expresado puntos de vista en el sentido de que el estudio de las matemáticas beneficia a los estudiantes fuera del conocimiento inmediato que aprenden (Xu, et al., 2020).
Hoy se podría decir esto diciendo que las matemáticas desarrollan habilidades genéricas como el pensamiento lógico, la capacidad de analizar cuestiones basadas en la razón y la conciencia de cómo los supuestos subyacentes pueden afectar las conclusiones del análisis o el pensamiento. Los autores se refieren a esta posición como la teoría de la disciplina formal (TDF), predice que el estudio de las matemáticas aumenta el nivel de respuestas lógicas normativas, es decir, las respuestas correspondientes a la lógica estándar subyacente a las matemáticas. Parecería que el TDF está ampliamente respaldado por la comunidad matemática, aunque sobre todo a un nivel implícito. Sin embargo, la investigación psicológica se ha mostrado escéptica sobre el TDF y sobre la posibilidad de transferir habilidades de un contexto a otro. El principal rival del TDF es la hipótesis de filtrado, que dice que las mejores habilidades de razonamiento en un estudiante se deben a una propensión inicial al estudio matemático más que a una consecuencia del mismo. Sin embargo, el TDF ha seguido influyendo en la política educativa, aunque de vez en cuando se enfrenta a desafíos a nivel público y político. Las matemáticas en general, y los enunciados condicionales en particular, presentan una mayor carga cognitiva que los enunciados de hechos o los listados de información (Morsanyi, 2021).
El objetivo de la enseñanza de las matemáticas es promover la comprensión y la apreciación genuinas del material para la mayoría de los estudiantes que tenemos frente a nosotros, o es presentar a los estudiantes más capaces una amplia gama de temas e ideas, a fin de prepararlos para estudiar en otras disciplinas o posibles carreras futuras como matemáticos. Este tipo de problema no es tan inmediato en disciplinas menos analíticas, y hay que encontrar un equilibrio entre promover la comprensión y la variedad de matemáticas en un plan de estudios dado (Carrillo, et al., 2018).
La comprensión requiere tiempo y esfuerzo, por parte del profesor y del alumno, y esto a veces se sacrifica para abarcar más material y más temas que se perciben como necesarios para su posterior estudio. No todo el mundo piensa que el pensamiento lógico se ajusta o debería ajustarse a las normas matemáticas y lógicas estándar, y las críticas al valor del estudio matemático son ahora bastante comunes, por lo que las respuestas a tales preguntas podrían ser más importantes en el futuro para la salud del estudio matemático de lo que han sido en el pasado. Puede ser conveniente que la cultura matemática las considere más seriamente de lo que ha sido el caso (Güner & Erbay, 2021).
Callingham & Siemon (2021), dicen que las matemáticas se definen como la ciencia de los patrones que también enfatiza el orden, la estructura, el patrón y la relación lógica. Los estudiantes de educación matemática deben desarrollar su capacidad para razonar y pensar de manera lógica. Es requerido por estudiantes de todas las disciplinas en general y de matemáticas en particular. La educación matemática tiene como objetivo desarrollar el pensamiento lógico entre los estudiantes que generalmente piensan en algoritmos, pero eso no es pensamiento lógico, ya que existe una diferencia entre el pensamiento lógico y solo pensar. Depender del mero pensamiento conduce a la memorización que, en última instancia, no desarrolla el pensamiento lógico. Los estudiantes sin pensamiento lógico en matemáticas pueden manejar una situación similar pero no pueden hacer algo cuando se enfrentan a una situación diferente. El aprendizaje lógico les permite comprender la situación y encontrar una solución de inicio de sesión que los lleve hacia el pensamiento lógico.
Umarji, et al. (2021), mencionaron que el pensamiento lógico pasa de lo conocido a lo desconocido siguiendo ciertas reglas y estándares objetivos que son la gramática de la lógica. El pensamiento lógico está ligado a la idea de que el estudio de las matemáticas puede probar que ciertas cosas son verdaderas en matemáticas y existen ciertas reglas gramaticales con las que se pueden organizar los conceptos relacionados con las matemáticas. El pensamiento lógico se basa en ciertas premisas y si las premisas tienen naturaleza matemática, se puede decir que la lógica matemática está funcionando (Vîșcu & Watkins, 2021).
El estudio de las matemáticas proporciona una comprensión significativa cuando se comprende mediante el uso del razonamiento. El nivel de razonamiento lógico aumenta con su uso constante en varios contextos y cuando se aprende en los primeros años. El pensamiento matemático desarrolló el pensamiento lógico que ayudó a los estudiantes a comprender las realidades que los rodeaban y a realizar acciones sensatas. Los logros en matemáticas se han asociado con el razonamiento y el pensamiento lógico. Se cree que el razonamiento sistemático es una característica destacada de la educación matemática en la que se puede explorar, identificar y justificar todo el contenido relacionado con las matemáticas (Pande & Bharathi, 2020).
El estilo de aprendizaje lógico-matemático es uno de los ocho tipos de estilos de aprendizaje, o inteligencias. El estilo de aprendizaje lógico-matemático se refiere a su capacidad para razonar, resolver problemas y aprender utilizando números, información visual abstracta y análisis de las relaciones de causa y efecto. Las personas con estilos de aprendizaje lógico-matemático utilizan el razonamiento y la secuencia lógica para absorber información. Sus puntos fuertes son las matemáticas, la lógica, la percepción de patrones y la resolución de problemas. Les gusta trabajar con números, encontrar métodos lógicos para responder preguntas, clasificar y categorizar. Se sienten cómodos trabajando con lo abstracto. Disfrutan de las actividades escolares como matemáticas, informática, tecnología, dibujo, diseño, química y otras ciencias duras. Los aprendices lógico-matemáticos prefieren el orden lógico en la instrucción y a menudo trabajan mejor en entornos estructurados y organizados. Tienen fuertes habilidades de análisis visual, memoria y resolución de problemas. Las personas con estilos de aprendizaje lógico-matemático aprenden mejor cuando se les enseña utilizando materiales visuales, computadoras, programas estadísticos y analíticos y proyectos prácticos. Prefieren actividades estructuradas y orientadas a objetivos que se basan en el razonamiento matemático y la lógica en lugar de actividades creativas menos estructuradas con objetivos de aprendizaje inexactos (Carey, et al., 2015).
De acuerdo con Caviola, et al. (2021), el pensamiento matemático es bastante diferente a hacer matemáticas como se usa típicamente en nuestros sistemas escolares. Es una forma de pensar que involucra las matemáticas para resolver problemas del mundo real. Una característica clave del pensamiento matemático es pensar fuera de la caja, que es muy importante en el mundo actual. El pensamiento matemático también mejora su mente en términos de pensamiento lógico. El pensamiento lógico, a su vez, también ayuda a los niños a sobresalir en otras materias. Los convierte en un mejor solucionador de problemas, lo que puede resultar útil incluso fuera del ámbito académico.
De Ribaupierre (2015); y Morsanyi (2021), sugieren que los beneficios son:
Mejorar sus habilidades matemáticas: el desarrollo de habilidades de pensamiento crítico matemático permite comprender las lecciones de matemáticas más rápido. En lugar de memorizar ciegamente las fórmulas y los conceptos, el estudiante aprecia los conceptos a un nivel más profundo y los recuerda durante mucho tiempo. Resultando en una mejora significativa en sus habilidades matemáticas.
Establecer una conexión entre la teoría y la práctica: una vez que el estudiante desarrolla el pensamiento matemático necesario y las habilidades de razonamiento creativo, correlaciona la teoría con las cosas y situaciones que encuentran a su alrededor con regularidad. Esto permite que el aprendizaje de las matemáticas sea mucho más entretenido para ellos, y también adquieren el hábito de hacer matemáticas mentales, lo que resulta bastante útil en la vida cotidiana, así como en cualquier campo al que se dediquen en el futuro.
Resolver problemas matemáticos de manera más inteligente: el mayor obstáculo que enfrentan los estudiantes que memorizan conceptos matemáticos es resolver problemas matemáticos, que no son sencillos o son una modificación de una pregunta fácil. Los estudiantes con buen pensamiento matemático y habilidades de razonamiento creativo siempre tienen una clara ventaja en este sentido. Dividen los problemas de matemáticas en partes más pequeñas y pensarán de manera creativa para llegar a una solución inteligente en el menor tiempo posible. Por lo tanto, siempre se adelantan a los demás estudiantes cuando se trata de responder los exámenes de matemáticas de la escuela.
Mejorar habilidades para la resolución de problemas: el pensamiento matemático mejora las habilidades de los estudiantes para resolver problemas y les ayuda a convertirse en pensadores lógicos en lugar de pensadores emocionales. Es la base de la mejora, la comunicación y el aprendizaje constantes. Les permite ejercer control sobre el entorno a través de mejores decisiones.
Piaget nació en Suiza a fines del siglo XIX y fue un estudiante precoz, y publicó su primer artículo científico cuando tenía solo 11 años. Gran parte del interés de Piaget en el desarrollo cognitivo de los niños se inspiró en las observaciones que hizo de su propio sobrino e hija. Estas observaciones reforzaron su hipótesis en ciernes de que las mentes de los niños no eran simplemente versiones más pequeñas de las mentes de los adultos. Hasta este punto de la historia, los niños eran tratados en gran medida simplemente como versiones más pequeñas de los adultos. Piaget fue uno de los primeros en identificar que la forma en que piensan los niños es diferente a la forma en que piensan los adultos. En cambio, propuso, la inteligencia es algo que crece y se desarrolla a través de una serie de etapas. Los niños mayores no solo piensan más rápido que los niños más pequeños, sugirió. En cambio, existen diferencias tanto cualitativas como cuantitativas entre el pensamiento de los niños pequeños y el de los niños mayores. Con base en sus observaciones, concluyó que los niños no eran menos inteligentes que los adultos, simplemente piensan de manera diferente. Albert Einstein calificó el descubrimiento de Piaget de tan simple que sólo un genio podría haber pensado en él (Byrnes, 2020).
Muthivhi (2015), escribe que la teoría de etapas de Piaget describe el desarrollo cognitivo de los niños. El desarrollo cognitivo implica cambios en los procesos y habilidades cognitivos. En opinión de Piaget, el desarrollo cognitivo temprano implica procesos basados en acciones y luego progresa a cambios en las operaciones mentales. La teoría del desarrollo cognitivo de Jean Piaget sugiere que los niños atraviesan cuatro etapas diferentes de desarrollo mental. Su teoría se centra no solo en comprender cómo los niños adquieren conocimientos, sino también en comprender la naturaleza de la inteligencia. Las etapas de Piaget son:
Etapa sensoriomotora: desde el nacimiento hasta los 2 años.
Etapa preoperacional: de 2 a 7 años.
Etapa operativa concreta: de 7 a 11 años.
Etapa operativa formal: mayores de 12 años.
Piaget (1981), creía que los niños desempeñan un papel activo en el proceso de aprendizaje, actuando como pequeños científicos mientras realizan experimentos, hacen observaciones y aprenden sobre el mundo. A medida que los niños interactúan con el mundo que los rodea, continuamente agregan nuevos conocimientos, se basan en el conocimiento existente y adaptan las ideas que tenían anteriormente para adaptarse a la nueva información.
La primera etapa (sensoriomotora): Principales características y cambios en el desarrollo: el infante conoce el mundo a través de sus movimientos y sensaciones; los niños aprenden sobre el mundo a través de acciones básicas como chupar, agarrar, mirar y escuchar; los bebés aprenden que las cosas continúan existiendo aunque no se puedan ver, es decir, la permanencia del objeto; son seres separados de las personas y objetos que los rodean; se dan cuenta de que sus acciones pueden hacer que sucedan cosas en el mundo que los rodea. Realmente solo se aplicó a niños de hasta dos años de edad. Pero las siguientes dos etapas son muy relevantes para los grados de primaria (Carey, et al., 2015).
Durante esta primera etapa del desarrollo cognitivo, los bebés y los niños pequeños adquieren conocimientos a través de experiencias sensoriales y la manipulación de objetos. Toda la experiencia de un niño en el período más temprano de esta etapa ocurre a través de reflejos básicos, sentidos y respuestas motoras. Es durante la etapa sensoriomotora que los niños atraviesan un período de crecimiento y aprendizaje dramáticos. A medida que los niños interactúan con su entorno, continuamente hacen nuevos descubrimientos sobre cómo funciona el mundo (Bicer, et al., 2021).
El desarrollo cognitivo que ocurre durante este período tiene lugar durante un período de tiempo relativamente corto e implica un gran crecimiento. Los niños no solo aprenden a realizar acciones físicas como gatear y caminar; también aprenden mucho sobre el lenguaje de las personas con las que interactúan. Piaget también dividió esta etapa en varias sub etapas diferentes. Es durante la parte final de la etapa sensoriomotora cuando surge el pensamiento representacional temprano.
Segunda etapa (preoperacional): Principales características y cambios en el desarrollo: los niños comienzan a pensar simbólicamente y aprenden a usar palabras e imágenes para representar objetos; los niños en esta etapa tienden a ser egocéntricos y luchan por ver las cosas desde la perspectiva de los demás; si bien mejoran con el lenguaje y el pensamiento, todavía tienden a pensar en las cosas en términos muy concretos. Es posible que las bases del desarrollo del lenguaje se hayan sentado durante la etapa anterior, pero es el surgimiento del lenguaje uno de los principales sellos distintivos de la etapa de desarrollo preoperacional (De Ribaupierre, 2015).
Piaget sugirió que los niños en los primeros grados de la escuela primaria necesitan objetos, imágenes, acciones y símbolos concretos para desarrollar significados matemáticos. Por ejemplo, al enseñar la estrategia de suma hacer diez para descubrir hechos básicos como 9 + 4, los estudiantes de primer grado deben mover contadores en marcos de diez dobles para representar la idea de usar parte de un sumando para "hacer" el otro suma en un "diez" completo. De esta manera verbalizan "nueve más cuatro tiene el mismo valor que diez más tres". Al hacerlo, los números se tratan como cantidades, en lugar de símbolos. Posteriormente, la instrucción se traslada a una representación pictórica del mismo problema (Casey & Ganley, 2021).
En esta etapa, los niños aprenden a través del juego de simulación, pero aún luchan con la lógica y adoptan el punto de vista de otras personas. También suelen tener dificultades para comprender la idea de constancia. Por ejemplo, un investigador puede tomar un trozo de arcilla, dividirlo en dos piezas iguales y luego darle a un niño la posibilidad de elegir entre dos piezas de arcilla para jugar. Una pieza de arcilla se enrolla en una bola compacta, mientras que la otra se rompe en forma de panqueque plano. Dado que la forma plana parece más grande, es probable que el niño antes de la operación elija esa pieza, aunque las dos piezas sean exactamente del mismo tamaño.
Tercera etapa (concreta operativa): Principales características y cambios en el desarrollo: durante esta etapa, los niños comienzan a pensar lógicamente sobre eventos concretos; empiezan a comprender el concepto de conservación; que la cantidad de líquido en una taza corta y ancha es igual a la de un vaso alto y delgado, por ejemplo, su pensamiento se vuelve más lógico y organizado, pero aún muy concreto; y los niños comienzan a usar la lógica inductiva o el razonamiento a partir de información específica hasta un principio general (Byrnes, 2020).
Si bien los niños todavía son muy concretos y literales en su pensamiento en este punto del desarrollo, se vuelven mucho más expertos en el uso de la lógica. El egocentrismo de la etapa anterior comienza a desaparecer a medida que los niños se vuelven mejores para pensar en cómo otras personas podrían ver una situación. Si bien el pensamiento se vuelve mucho más lógico durante el estado operativo concreto, también puede ser muy rígido. Los niños en este punto del desarrollo tienden a tener problemas con conceptos abstractos e hipotéticos (Viarouge, et al., 2019).
Comienza alrededor del segundo grado. En estos grados, los estudiantes se vuelven más sofisticados en su pensamiento y comienzan a visualizar mentalmente las manipulaciones concretas y pictóricas a medida que las aplican a problemas más abstractos. Por ejemplo, si tienen una estrategia para 9 + 4, pueden continuar pensando cuantitativamente y aplicar el mismo pensamiento a 29 + 15. De la misma manera que "nueve más cuatro tienen el mismo valor que diez más tres", entonces "Veintinueve más quince tiene el mismo valor que treinta más catorce". El mismo pensamiento se puede aplicar a 298 + 56, lo que elimina la necesidad de aplicar un algoritmo tradicional de papel y lápiz.
Durante esta etapa, los niños también se vuelven menos egocéntricos y comienzan a pensar en cómo otras personas podrían pensar y sentir. Los niños en la etapa operativa concreta también comienzan a comprender que sus pensamientos son únicos para ellos y que no todos los demás necesariamente comparten sus pensamientos, sentimientos y opiniones.
Cuarta etapa (operativa formal): Principales características y cambios en el desarrollo: el adolescente o adulto joven comienza a pensar de manera abstracta y a razonar sobre problemas hipotéticos; surge el pensamiento abstracto; los adolescentes comienzan a pensar más en cuestiones morales, filosóficas, éticas, sociales y políticas que requieren un razonamiento teórico y abstracto; comienza a utilizar la lógica deductiva o el razonamiento desde un principio general hacia información específica (Muthivhi, 2015).
La etapa final de la teoría de Piaget implica un aumento de la lógica, la capacidad de utilizar el razonamiento deductivo y la comprensión de las ideas abstractas. En este punto, las personas se vuelven capaces de ver múltiples soluciones potenciales a los problemas y pensar de manera más científica sobre el mundo que les rodea. La capacidad de pensar en ideas y situaciones abstractas es el sello distintivo de la etapa operativa formal del desarrollo cognitivo. La capacidad de planificar sistemáticamente el futuro y razonar sobre situaciones hipotéticas también son habilidades críticas que surgen durante esta etapa (Paulus & Essler, 2020).
Es importante señalar que Piaget no veía el desarrollo intelectual de los niños como un proceso cuantitativo; es decir, los niños no solo agregan más información y conocimiento a su conocimiento existente a medida que crecen. En cambio, Piaget sugirió que hay un cambio cualitativo en la forma de pensar de los niños a medida que avanzan gradualmente a través de estas cuatro etapas. Un niño a los 7 años no solo tiene más información sobre el mundo que a los 2 años; hay un cambio fundamental en su forma de pensar sobre el mundo (Newman & Newman, 2020).
Materiales y métodos
La investigación se hizo con un corte transversal del mes de enero y marzo del 2021, a través de un estudio de enfoque cuantitativo de correlaciones que medía el efecto de la psicología piagetena o variable independiente en la educación de la matemática que se la deduce como la variable dependiente. La intención fue la de determinar lo que piensan los docentes del área de matemáticas de dos escuelas públicas sobre la premisa planteada y con ello validar una propuesta doctoral de la autora principal de este artículo. Se aplicó una encuesta con 10 ítems al total de una población, es decir, se emplea la muestra por conveniencia, que fueron 36 personas de las dos unidades educativas. El alfa de Cronbach resultó en 0.90.
La variable independiente se la llamó Formal Operacional, y se la estableció así porque las primeras 4 preguntas hechas a los docentes, están ligadas a los 4 tipos de desarrollo que el adolescente debe presentar entre los 11 y 17 años de edad. Cada pregunta se codificó como dimensión de la variable con los siguientes nombres: Razonamiento_hipot_deduc; Razonamiento_induc; Abstracciones y Razona_abst.
La variable dependiente fue llamada educación de la matemática, en el estudio, fueron integradas a las 4 últimas preguntas, que se relacionaban con la actividad docente y los mismos tipos de desarrollo adolescente, la intención de las preguntas y la variable es que el profesor identifique si el permite el desarrollo piagetano en la clase. Las dimensiones de las preguntas coordinadas con la variable se las denominó de la siguiente manera: Educación concreta; Creatividad; Razonamiento y Reflexiona.
Resultados y discusión
Se realizó la tabulación por frecuencias en la opción estadísticos descriptivos del SPSS y se obtuvo la siguiente información (Tabla 1):
Tabla 1 - Estadística descriptiva por frecuencia.
| Preguntas | Muy desacuerdo | Desacuerdo | Indiferente | De acuerdo | Muy de acuerdo |
|---|---|---|---|---|---|
| ¿El estudiante usa el razonamiento hipotético / deductivo? | 8,9% | 28,9% | 6,7% | 42,2% | 13,3% |
| ¿El estudiante usa el razonamiento inductivo? | 6,7% | 37,8% | 6,7% | 37,8% | 11,1% |
| ¿El estudiante hace abstracciones reflexivas? | 13,3% | 31,1% | 6,7% | 37,8% | 11,1% |
| ¿El estudiante demuestra capacidad para razonar de manera puramente simbólica / abstracta? | 11,1% | 37,8% | 8,9% | 33,3% | 8,9% |
| Usted como docente ¿Utiliza estrategias y materiales didácticos operativos concretos? | 11,1% | 26,7% | 11,1% | 33,3% | 17,8% |
| Usted como docente ¿Brinda a los estudiantes la oportunidad de explorar muchas preguntas hipotéticas? | 15,6% | 37,8% | 8,9% | 28,9% | 8,9% |
| Usted como docente ¿Da oportunidades para resolver problemas y razonar científicamente? | 11,1% | 24,4% | 6,7% | 48,9% | 8,9% |
| Usted como docente ¿Enseña conceptos amplios, no solo hechos, utilizando material e ideas relevantes para los estudiantes? | 17,8% | 51,1% | 6,7% | 20,0% | 4,4% |
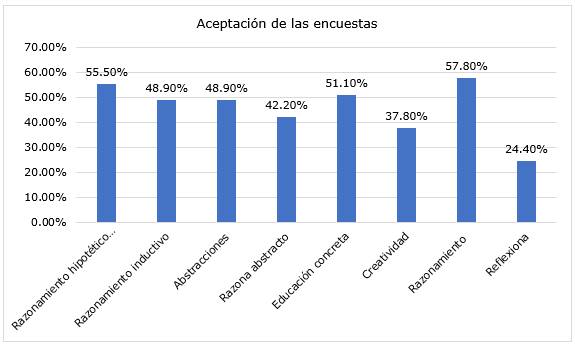
La lectura de estos datos explica en detalle la forma en la que se tabularon las respuestas, pero se hace de forma resumida, según las dimensiones establecidas, una figura con la aceptación a las preguntas planteadas (sumatoria de muy de acuerdo y de acuerdo), encontrando que 57,8% indican que los docentes buscan que los estudiantes razonen, 55,5 observan que tienen un razonamiento hipotético, 51,10% enseñan de forma concreta; 48,9% observan un razonamiento inductivo al igual que abstracciones en sus reacciones; el 42,20% cree que los estudiantes formaron su pensamiento abstracto; 37,80% permiten la creatividad en sus clases y 24,4% permite la reflexión en el aula (Fig. 1).
Una vez encontrados los datos descriptivos, para la demostrar la hipótesis, se hizo una prueba de normalidad de las dos variables planteadas en el estudio (Tabla 2).
Tabla 2 - Pruebas de normalidad.
| Kolmogorov-Smirnova | Shapiro-Wilk | |||||
| Estadístico | gl | Sig. | Estadístico | gl | Sig. | |
| Formal Operacional | ,168 | 45 | ,003 | ,926 | 45 | ,007 |
| Educación de la matemática | ,100 | 45 | ,200* | ,962 | 45 | ,148 |
*. Esto es un límite inferior de la significación verdadera. a. Corrección de significación de Lilliefors
Se tomó como referente al análisis de normalidad de Shapiro-Wilk por tener el estudio, una población menor a 50 sujetos en la encuesta; Al ser el P valor mayor a 0,05 en ambas variables significó que tienen distribución normal, por lo que se consideró que las pruebas deben ser paramétricas.
La hipótesis planteada es que:
H1: La teoría de Piaget desde lo formal operacional es aplicada en la Educación de la matemática.
H0: La teoría de Piaget desde lo formal operacional no es aplicada en la Educación de la matemática.
Tabla 3 - Pruebas de chi-cuadrado.
| Valor | gl | Sig. asintótica (2 caras) | |
|---|---|---|---|
| Chi-cuadrado de Pearson | 335,034a | 210 | ,000 |
| Razón de verosimilitud | 159,570 | 210 | ,996 |
| Asociación lineal por lineal | 40,567 | 1 | ,000 |
| N de casos válidos | 45 | ||
| a. 240 casillas (100,0%) han esperado un recuento menor que 5. El recuento mínimo esperado es ,02. | |||
La significancia asintótica (tabla 3) es menor al alfa 0,05 en ambos casos, por lo tanto se rechaza la hipótesis nula, pero como se vio en el análisis descriptivo, los valores no llegaban al 60%, es decir, que si se aplica según los docentes la teoría de Piaget pero de forme deficiente. Lo que aprueba lo planteado por la autora principal en su tesis doctoral.
Para conocer si ambas variables guardan relación, como se supone que deba ser, pero se debe demostrar, se hizo un análisis de correlación de tau_b de Kendall para prueba paramétricas y el resultado es 0.855 lo que indica que la educación en matemáticas es afectada en el 85,5%, por la teoría Piaget en la Formal Operacional (Tabla 4).
Tabla 4 - Correlaciones
| Formal Operacional | Educación de la matemática | |||
|---|---|---|---|---|
| Tau_b de Kendall | Formal Operacional | Coeficiente de correlación | 1,000 | ,855** |
| Sig. (unilateral) | . | ,000 | ||
| N | 45 | 45 | ||
| Educación de la matemática | Coeficiente de correlación | ,855** | 1,000 | |
| Sig. (unilateral) | ,000 | . | ||
| N | 45 | 45 | ||
| **. La correlación es significativa en el nivel 0,01 (1 cola). | ||||
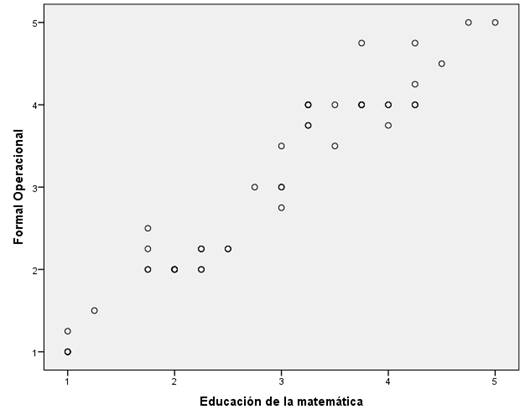
Los datos están agrupados (Fig. 2) hacia el centro y hacia la derecha, en la figura, lo que permite aceptar de que las dos variables guardan relación y sus datos no están dispersos en el estudio.
El estudio encontró que los docentes han estado utilizando los principios de Piaget en sus enseñanzas, pero en todos los casos, se presenta que de forma deficiente; en cuanto a si ellos permiten que los estudiantes interactúen de acuerdo a los principios piagetanos, estos valores resultaron igual de bajos (apenas superior al 50%), pero en el caso de enseñar fuera de los parámetros de los libros, apenas el 24,4% considera que lo hace, limitando la expresión del niño, lo que coincide con no dejar que los menores hipoteticen en el aula, pues aquí el resultado tuvo una aceptación leve, de apenas el 37,8%.
Como ejercicio científico, para corroborar un problema empírico, planteado por la autora principal de esta investigación, se prueba con la hipótesis de que, la teoría de Piaget, desde lo formal operacional, es aplicada en la Educación de la matemática en los dos centros de estudios investigados, pero los resultados descriptivos dejan observar que esto se cumple a medias. La correlación manifiesta que ambas variables planteadas guardan relación y que además la forma operacional incide en el 85.5% de la educación de la matemática, por lo que un modelo sería apropiado para mejorar los resultados aquí observados.
Conclusiones
En cuanto a la indagación en la literatura, se considera que esta es amplia y completa en los análisis de la relación de la psicología de Piaget y de la Matemática, pero no existen obras técnicas que enseñen el camino a seguir al docente para su utilización.
La intención de este documento fue la de determinar lo que piensan los docentes del área de matemáticas de dos escuelas públicas sobre psicología Piagetana en la educación de la matemática en estudiantes y se llegó a la conclusión de que ellos aplican de forma incompleta estos cuatro principios antes detallados. Es decir, que consideran de utilidad el hacerlo, pero se demuestra que no han logrado con éxito culminar su utilización.
Se pretendía validar una propuesta doctoral de la autora principal de este artículo y se concluye que, el análisis permitió reconocer los problemas que se están presentando y estos en especial resultaron entre la libertad de los menores a expresarse y que el docente debe ceder a escuchar las reflexiones de los estudiantes, algo muy poco usado en la enseñanza de la matemática.
Promover la publicación científica, de un modelo a seguir, para la implementación de la psicología piagetana en la enseñanza de la matemática.
Se recomienda hacer un estudio etnográfico cualitativo y observacional, que evidencia las necesidades del docente para la correcta aplicación de la teoría piagetana, como un elemento más en la enseñanza de la matemática e impulsar la creación de la investigación doctoral aquí propuesta en beneficio de la comunidad educativa.