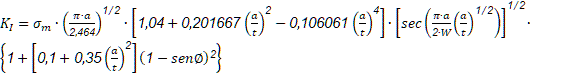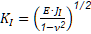INTRODUCCIÓN
El factor de intensidad de tensiones en modo “I” de carga (KI) se emplea en la mecánica de la fractura para caracterizar el estado de tensiones cerca de la punta de una grieta, causada por cargas remotas. Este factor usualmente es aplicado a materiales isotrópicos con comportamiento lineal-elástico, con vistas a suministrar criterios de fallas en materiales frágiles, aunque puede extenderse a aquellos que presentan deformación plástica a pequeña escala en la punta de grieta. Con vistas a modelar el comportamiento elasto-plástico de los materiales se introdujo el concepto de integral de contorno o “Integral J”, que se aplica para materiales con comportamiento lineal-elástico isotrópico o plástico isotrópico.
A pesar de que en la actualidad existen cientos de expresiones matemáticas para el cálculo de KI, muchos de los problemas industriales que se presentan no pueden ser resueltos mediante estas, por la diversidad de geometrías, sistemas de cargas y tipos de discontinuidades que aparecen. El análisis por elementos finitos (AEF) es una herramienta computacional que ha ganado popularidad a partir de las décadas de los 80 y 90 del pasado siglo, que resulta muy útil para ejecutar el cálculo del K e Integral J, en prácticamente cualquier caso (Sundaresan y col., 2015; Pawar y col., 2016; Kudari y Kodancha, 2017; Soutoa y col., 2020).
El presente trabajo se propone como objetivo implementar y validar el cálculo del factor de intensidad de tensiones y la integral J a través de los métodos de extrapolación de desplazamientos, integral de dominio y de integral de interacción, mediante la modelación por elementos finitos de problemas de piezas fisuradas en 2D y 3D.
MATERIALES Y MÉTODOS
2.1. Expresiones analíticas para el cálculo de KI
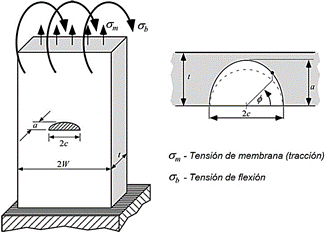
En la literatura se reportan expresiones analíticas para el cálculo de KI en geometrías conocidas. Una de estas expresiones (Ecuación 1) es la ofrecida en la norma ASTM E647-15, para el cálculo de KI en una probeta compacta, con geometría como la que se muestra en la Figura 1 (Anderson, 2017; ASTM E647-15, 2015).
Donde: “P” representa la fuerza aplicada (N); “B” espesor de probeta (m); “W” distancia desde el centro de los agujeros hasta el borde de la misma (m); “α” una relación 𝛼= 𝑎 𝑊 ; “a” distancia del centro de los agujeros hasta la punta de la grieta (m); KI se obtiene en (𝑃𝑎 𝑚 ).
Anderson (2017) ofrece una expresión analítica (Ecuación 2) para determinar KI en una placa plana, de dimensiones finitas, con una grieta semielíptica superficial, Figura 2. Para el caso particular de una grieta semicircular (a = c = radio de grieta), sometida solo a una tensión de tracción, la expresión se reduce a la que se expone a continuación.
Donde: σm representa una tensión aplicada de tracción (Pa); “a” radio de grieta (m); “t” espesor de probeta (m); “W” semiancho (m); “∅” posición angular del punto de interés en radianes; KI se obtiene en (𝑃𝑎 𝑚 ).
2.2. Sobre el mallado del modelo
Producto del elevado gradiente en los campos de tensiones y deformaciones en la punta de la grieta, la malla se debe refinar cerca de ella, empleando configuración de “tela de araña” (Anderson, 2017; ANSYS INC., 2017). Para obtener resultados razonables, la primera fila de elementos alrededor de la punta de la grieta debe ser de elementos singulares, con los nodos medios colocados a ¼ de la dimensión del lado. Estos deben tener un radio menor o igual a a/8, donde “a” es la longitud de la grieta. Se recomienda, en la dirección circunferencial, aproximadamente un elemento cada 30° o 40°. Los elementos de la punta de la grieta no deben distorsionarse y deben tomar la forma de triángulos isósceles. El comando KSCON del preprocesador genera automáticamente elementos singulares alrededor del keypoint especificado, en modelos 2D, aunque no está disponible para modelos 3D (ANSYS INC., 2017). El tipo de elemento recomendado para un modelo de fractura 2D es el PLANE183, cuadrático de 8 nodos, mientras para los modelos 3D se recomienda el SOLID186, ladrillo de 20 nodos (ANSYS INC., 2017).
2.3. Cálculo de KI a partir de la Integral J
El programa calcula la integral J en la etapa de solución, basado en el método de integral de dominio, a partir del comando CINT, y almacena el valor en el archivo de resultados. La aplicación de CINT requiere los siguientes pasos, que se ejemplifican con los comandos usados en este trabajo (ANSYS INC., 2017).
• Paso 1: Iniciar un nuevo cálculo de Integral J.CINT,NEW,1 (declara nuevo análisis)
• Paso 2: Definir la información de la grieta. Definir el componente del nodo de la punta de la grieta y la normal del plano de la grieta. CINT,NAME,CRACKTIP CINT,NORM,0,2 (define como normal al eje “y” del sist. coord. cartesiano)
• Paso 3: Especificar el número de contornos. CINT,NCON,6 (especifica 6 contornos de integración)
• Paso 4: Definir una condición de simetría de fisuras. CINT,SYMM,ON (declara condición de simetría en el plano de la grieta)
Para la condición de deformación plana existe una relación (Ecuación 3) entre JI y KI, para un modelo de material lineal-elástico (Anderson, 2017).
Donde: “E” representa el Módulo de elasticidad del material (Pa); JI se sustituye en (Pa?m); 𝜈 el coeficiente de Poisson; KI se sustituye en (𝑃𝑎 𝑚 ).
2.4. Cálculo de KI directamente
El cálculo de KI se puede realizar directamente a través del método de integral de interacción y el empleo del mismo comando CINT.
CINT,NEW,1 (declara nuevo análisis)
CINT,TYPE,SIFS (define tipo de cálculo a realizar- KI)
CINT,CTNC,CRACKTIP,NODOCARAGRIETA (define componente de nodo en la punta de grieta y nodo en la cara de esta)
CINT,NORM,0,2 (define como normal al eje “y” del sist. coord. cartesiano)
CINT,SYMM,ON (declara condición de simetría en el plano de la grieta)
CINT,NCON,6 (especifica 6 contornos de integración)
El cálculo de KI también se puede realizar a partir del método de extrapolación de desplazamientos y el comando KCALC, en la fase de post procesamiento.
Paso 1: Define un camino a lo largo de la cara de la grieta
El primer nodo de la ruta debe ser el nodo de la punta de la grieta. Para un modelo de media fisura, se requieren dos nodos adicionales, ambos a lo largo de la cara de la fisura.
PATH,KI,3,,, (define nombre de trayectoria, número de puntos de esta, 3)
PPATH,1,100 (define nodos en trayectoria, primero coincide con punta de la grieta)
PPATH,2,107
PPATH,3,106
Paso 2: Calcular KI.
KCALC,0,1,0,0 (define deformación plana, número de material, condición de simetría y que no entregue los desplazamientos locales)
Este método exige elementos singulares alrededor de la punta de grieta y una malla fina en la zona cercana a esta, a diferencia de los primeros dos métodos que emplean integración de área o volumen, donde esto no es indispensable.
2.5. Casos analizados para la determinación de KI empleando el análisis por elementos finitos
2.5.1. Caso No. 1-Determinación de KI en probeta compacta y simulación en 2D
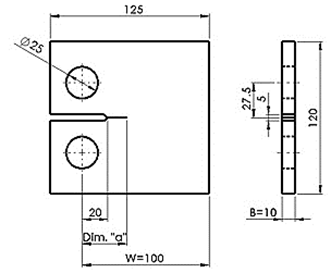
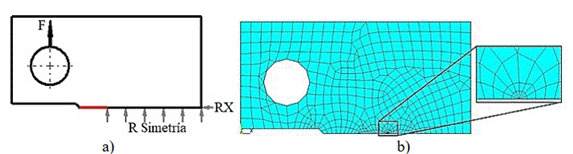
Como caso de análisis No. 1 se decidió determinar KI en una Probeta Compacta, con geometría según norma (ASTM E647-15, 2015), empleando un modelo de AEF bidimensional. Se asumieron las dimensiones mostradas en Figura 3. La dimensión “a” se varió entre 30 y 60 mm, lo que provoca que longitud de grieta varió ampliamente entre 10 y 40 mm; como se trabaja con un modelo de material lineal-elástico no es necesario imponer límites precisos a esta dimensión, con vistas a controlar la dimensión de la zona de deformación plástica en la punta de la grieta. Se asumió un módulo de Young de 210 GPa, y un coeficiente de Poisson de 0,3, valores característicos para aceros.
Arbitrariamente se aplicó una fuerza de 7000 N, que se introduce al modelo como carga aplicada por unidad de espesor (700000 N/m), ya que se modela en condición de “deformación plana”. Se modeló la mitad superior de la probeta aprovechando la simetría axial geométrica y de carga aplicada. Se declararon las restricciones de desplazamiento mostradas en Figura 4.
La malla se construyó con ocho elementos singulares de dimensión 1 mm, alrededor de la punta de la grieta y en el resto del modelo se emplearon elementos cuadriláteros, que se hacen más bastos a cierta distancia. La creación de los elementos singulares alrededor de la punta se realiza de manera automática, empleando el comando KSCON (vea Figura 4). En todo momento se emplea el elemento PLANE183.
2.5.2. Caso No. 2-Determinación de KI en probeta compacta y simulación en 3D
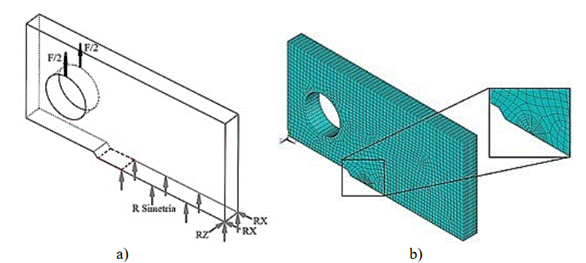
Se decidió, además, determinar KI a través de los métodos de integral de dominio e integral de interacción, para una probeta compacta, con las mismas dimensiones y condiciones del subepígrafe 2.5.1, pero modelando en 3D (Figura 5). Se modeló la mitad superior de la probeta, aprovechando la condición de simetría. Como condiciones de frontera, se aplicó sobre dos keypoint en la parte superior del agujero la mitad de la fuerza de 7000 N. Se declararon las restricciones de desplazamiento mostradas en la Figura 5.
Para el mallado se crea el área de la superficie frontal de la probeta compacta en 2D, similar al subepígrafe anterior. Se construye un área semicircular, con centro en la punta de la grieta, luego se malla esta área mediante el comando KSCON, que genera automáticamente elementos singulares alrededor de dicha punta, empleando elementos PLANE183. Se crearon seis elementos singulares alrededor de la punta, con dimensión de 1 mm. El resto del área de la probeta fuera del semicírculo se malla con elementos cuadriláteros, que se hacen más bastos en las zonas más alejadas de la punta de grieta. Para obtener el modelo 3D, se extruyen estas áreas en dirección perpendicular, declarando el espesor de probeta, como magnitud de extrusión; en este paso se forma la malla con elementos hexaédricos SOLID186 (Figura 5). Finalmente se eliminan de la malla los elementos bidimensionales. A pesar de que el comando KSCON no es aplicable directamente para el mallado tridimensional, lo que es una importante limitante, se aprovecha sus ventajas partiendo de una malla en 2D.
2.5.3. Caso No. 3-Determinación de KI en placa con grieta semicircular superficial mediante simulación en 3D
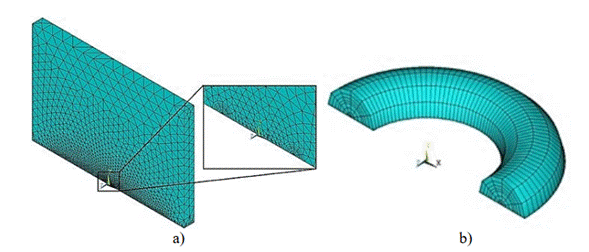
Como caso de análisis No. 3 se decidió determinar KI para una placa con grieta superficial semicircular, sometida a una tensión uniforme de tracción (Figura 6). Se asumió un módulo de Young de 210 GPa y un coeficiente de Poisson de 0,3. Se asumió un semiancho de probeta (W) de 300 mm y un espesor (t) de 40 mm. Se aplicó arbitrariamente una tensión de tracción uniforme (σ) de 150 MPa. Se consideró una geometría de grieta semicircular superficial con radios (a = c) de 10, 20 y 30 mm. Se modeló solo la mitad de la placa, aprovechando la condición de simetría. Se declararon las restricciones de desplazamiento mostradas en Figura 6.
La malla se construyó desarrollando un cuarto de toro con mallado del tipo “tela de araña”, con elementos singulares alrededor del frente de grieta circunferencial, Figura 7. La porción de toro se malló empleando elementos hexaédricos y el resto del modelo mediante elementos tetraédricos. Para el mallado del cuarto de toro se construyó un área semicircular, con centro en la punta de la grieta, luego esta se malló mediante comando KSCON y elementos PLANE183, se extruyó esta área semicircular siguiendo la trayectoria de una semicircunferencia con radio igual al de la grieta, construida en plano perpendicular a dicha área inicial (en este paso se forma la malla con elementos hexaédricos SOLID186) y finalmente se eliminan de la malla los elementos PLANE183.
RESULTADOS Y DISCUSIÓN
3.1. Resultados de KI determinados mediante simulación por elementos finitos en probeta compacta modelada en 2D, caso No. 1
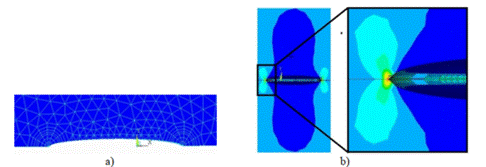
La Figura 8 muestra la malla deformada y la concentración de tensiones que ocurre en la punta de la grieta. Como se emplea un modelo de material lineal elástico, esto provoca que el modelo sobredimensione el valor de la tensión máxima que se produce en la punta de la grieta, ya que no ocurre la relajación por deformación plástica local del material.

Figura 8 a) Malla deformada. b) Campo de tensiones de Von Misses, modelo de material lineal elástico
La Tabla 1 resume los resultados del cálculo de KI a través de la expresión analítica (1) y del modelo de elementos finitos en 2D, y los métodos de integral de dominio e integral de interacción.
Tabla 1 Resultados de KI e Integral J para probeta compacta en 2D
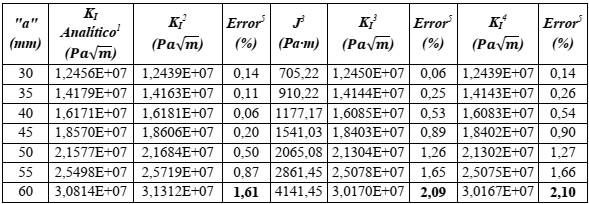
Notas: 1.- Valor según expresión 1; 2.- Según método de extrapolación de desplazamientos; 3.- Según método de integral de dominio; 4.- Según método de integral de interacción; 5.- Error relativo entre KI determinado según expresión analítica y según modelos, error = (KIanalítico-KImodelo)/KIanalítico·100.
En todos los casos el error relativo muestra un comportamiento creciente en la medida que aumenta la dimensión “a”, el que puede estar influenciado por la configuración de la malla y las dimensiones de los elementos alrededor de la punta de la grieta, que permanece invariable en todos los modelos. Por otro lado, el máximo error relativo fue prácticamente el mismo tanto para el método de integral de dominio, como para el de integral de interacción, 2,1 %. Para el método de extrapolación de desplazamientos el máximo error es de 1,61 %. Ambos errores, inferiores al 3 %, corroboran la calidad y confiabilidad del modelo de elementos finitos bidimensional, y el empleo de los tres métodos de determinación de KI.
3.2. Resultados de KI determinados mediante simulación por elementos finitos en probeta compacta modelada en 3D, caso No. 2
La Tabla 2 resume los resultados del cálculo de KI a través de la expresión analítica (1) y del modelo de elementos finitos en 3D. Todos los modelos concuerdan en que KI es máximo en donde el frente de grieta coincide con el centro del espesor de la probeta y es menor en la superficie de la misma, lo que coincide con lo reportado en la literatura para un modelo similar de probeta compacta (Kudari y Kodancha, 2017). Se obtuvo un valor máximo de KI de 13,28 MPa 𝑚 , para la grieta con dimensión “a” de 30 mm y de 32,26 MPa 𝑚 , para dimensión “a” de 60 mm.
Tabla 2 Resultados de KI e Integral J para probeta compacta en 3D

Notas: 1.- Encima, valor en superficie de probeta; debajo, valor al centro del espesor; 2.- Valor según expresión 1; 3.- Según método de integral de dominio; 4.- Según método de integral de interacción; 5.- Error = (KIanalítico-KImodelo)/KIanalítico·100.
El máximo error relativo de 6,6 % fue prácticamente el mismo, tanto para el modelo y el método de integral de dominio, como para el de integral de interacción, solo ligeramente superior al valor deseado de 5 %, pero que se considera adecuado ya que aún se aleja del 10 %, que en consideraciones ingenieriles es aún aceptable. De esta manera, se garantiza la calidad y confiabilidad del modelo de elementos finitos tridimensional, y el empleo de los dos conocidos métodos de integración para determinar KI. Sin embargo, se debe resaltar que el error máximo del cálculo de KI, empleando este modelo de elementos finitos tridimensional, triplica el error obtenido empleando el modelo bidimensional.
3.3. Resultados de KI determinados mediante simulación por elementos finitos en probeta con grieta semicircular superficial modelada en 3D, caso No. 3
La Figura 9 muestra la malla deformada en la cercanía de la grieta y la concentración de tensiones que ocurre en la punta de la misma, considerando un modelo de material lineal-elástico. La Tabla 3 resume los resultados del cálculo de KI a través de la expresión analítica (2) y del modelo de elementos finitos en 3D. Se calcula KI para tres radios del frente de grieta, 10, 20 y 30 mm, en cuatro ubicaciones angulares (Φ=0o, 30o, 60o y 90o), ver Figura 2. Todos los modelos concuerdan con la expresión analítica, en que KI es máximo en el punto donde el frente de grieta toca la superficie de la placa (Φ=0o) y disminuye en la medida que se recorre dicho frente hasta llegar al punto más alejado de dicha superficie (Φ=90o). Se obtuvo un valor de KI de 19,99 a 19,43 MPa 𝑚 , para la grieta de radio 10 mm, de 30,39 a 29,76 MPa 𝑚 , para radio de 20 mm y de 41,56 a 40,77 MPa 𝑚 , para radio 30 mm.
El error relativo resulta inferior a 3 % para el modelo y el método de integral de dominio, e inferior al 5 % para el método de integral de interacción. De esta manera se garantiza la calidad y confiabilidad del modelo de elementos finitos tridimensional, y el empleo de los dos conocidos métodos de integración para determinar KI, a lo largo del frente de grieta de geometría semicircular. Se garantiza la calidad del mallado alrededor del frente de grieta mediante el toroide construido.
Tabla 3 Resultados de KI e Integral J para probeta con grieta semicircular superficial
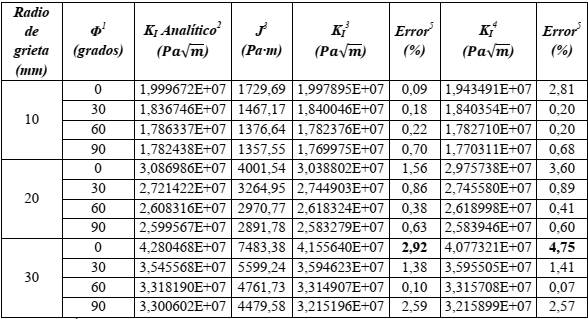
Notas: 1.- Ángulo de frente de grieta; 2.- Valor según expresión 2; 3.- Según método de integral de dominio; 4- Según método de integral de interacción; 5- Error = (KIanalítico-KImodelo)/KIanalítico·100.
Adicionalmente fue comprobado que, para los tres casos analizados, en la variación del error relativo de KI de los modelos de elementos finitos, respecto al valor analítico reportado en la literatura, solo influye la variación de las dimensiones de la grieta, como demuestran las tablas 1, 2, 3, pero no el valor de la carga o tensión aplicada sobre la probeta (aunque lo anterior no se tabula). Se evidenció que el aumento o disminución del valor de la carga o tensión aplicada (tabulado para 7000 N aplicados sobre probeta compacta y 150 MPa sobre probeta con grieta semicircular), provoca el aumento o disminución de la magnitud de KI, pero el error relativo se mantiene invariable, siempre que se mantengan inalterables los demás elementos de los modelos.
CONCLUSIONES
En todos los casos abordados, el error de los resultados de KI que brindan los modelos de elementos finitos, respecto a los obtenidos por soluciones analíticas conocidas, no supera el 3 % para los modelos bidimensionales y el 7 % para los tridimensionales, lo que permite considerar validada la implementación de los mismos.
Se logra un eficiente mallado del frente de grieta en 3D, del tipo “tela de araña”, aprovechando las ventajas del comando KSCON, mallando primero un área semicircular en 2D, con centro en la punta de grieta, y luego extruyendo la misma para obtener la porción tridimensional de cilindro o toro mallado que se requiera.
Se comprobó que, en todos los casos analizados, el aumento o disminución del valor de la carga o tensión aplicada sobre el modelo de elementos finitos, provoca un aumento o disminución del valor de KI calculado, pero siempre el error relativo respecto a la solución analítica se mantiene invariable, para cada dimensión de grieta.