INTRODUCCIÓN
El diseño de una estructura es condicionado por muchos factores, como por ejemplo la resistencia de los materiales, las acciones permanentes, las cargas variables y también por las vibraciones. Las vibraciones pueden causar daños significativos en las estructuras (Batou y Adhikari, 2019), tales como deformaciones, tensiones, agrietamientos, fatiga, pudiendo llegar al colapso si se alcanza la frecuencia propia de la estructura. Se denomina frecuencia de resonancia a la frecuencia en la que se alcanza el máximo grado de oscilación. Todo cuerpo o sistema tiene una o varias frecuencias características (Ahumada, 2010).
Estudiar el comportamiento dinámico de las estructuras permite conocer las frecuencias predominantes bajo la acción de la fuerza de excitación, los modos principales de oscilación, así como los desplazamientos que se generan en estos sistemas que están sometidos a las vibraciones. En el último siglo ha existido una tendencia a diseñar edificios cada vez más esbeltos, construir puentes muy largos para acortar grandes distancias entre sitios que se ven separados por ríos, bahías o cañones, construcciones livianas, estructuras más delgadas y con escasos apoyos para mejorar la estética y lograr el abaratamiento de los costos de fabricación (Petrini y col., 2020), (Alhamashi y Al-Ashtari, 2022). Desde el punto de vista estructural, esto conduce naturalmente a altas flexibilidades, períodos naturales elevados y consecuentemente a grandes desplazamientos por cargas dinámicas tales como viento, terremotos u otras fuerzas excitantes. Los niveles de peligrosidad y daños provocados por estas cargas pueden ser desde despreciables hasta generar grandes estragos económicos y sociales. Es por esta razón que ha surgido la necesidad de diseñar y construir estructuras resistentes a las implicaciones que este fenómeno presenta, con la finalidad de evitar el colapso parcial o total de las mismas (Barja y col., 2020), (Junfeng y col., 2022).
Se han presentado innumerables metodologías para dar solución a problemas de seguridad estructural provocados por vibraciones y fuerzas externas en puentes y otras edificaciones. Una de las alternativas más interesantes es la disipación de energía a través de sistemas de control de vibraciones acoplados a la estructura, en concreto, el uso de Amortiguadores de Masa Sintonizados (AMS) (Den, 1956).
Un Amortiguador de Masa Sintonizado (TMD, del inglés, Tuned Mass Damper), es un dispositivo compuesto por una masa, un resorte y un amortiguador que, al acoplarse a una estructura, controla y reduce su respuesta dinámica, a una frecuencia determinada (Jafari y Alipour, 2021), (Lai y col., 2023). La frecuencia del TMD se sintoniza con la frecuencia natural de la estructura portante, de tal forma que, al ser excitada, el TMD vibre en resonancia, disipando la energía absorbida y reduciendo en gran medida las oscilaciones provocadas por dicha alteración. Este fin se consigue variando los tres parámetros que definen un TMD: masa, amortiguación y rigidez (Hajji, 2016), (Di Matteo y col., 2017), (Chagoyen y col., 2021).
En este trabajo se determinan los parámetros del TMD (masa, amortiguación y rigidez) que hacen posible su eficiencia en la función que desempeña: reducir la respuesta dinámica de la estructura ante la acción de fuerzas externas. Se realiza el cálculo de tres variantes de resortes y la selección de un amortiguador, y se hace una propuesta donde se observa la disposición de los elementos en un diseño de TMD. Es decir, este trabajo tiene como objetivo diseñar los principales componentes y parámetros de un Amortiguador de Masa Sintonizado.
MATERIALES Y MÉTODOS
2.1. Determinación de la masa, el amortiguamiento y la rigidez del TMD
El objetivo de los TMD es reducir las vibraciones en los sistemas estructurales a los que se acoplan. El “caso de estudio” en este trabajo consiste en un puente ferroviario ubicado en el km 560 del ferrocarril central de Cuba. Las características del puente y de las fuerzas son conocidos, por lo que los parámetros que se pueden variar son los asociados al propio TMD: la masa, la amortiguación y la rigidez. En la tabla 1 se resumen los datos del puente “caso de estudio” al cual se le colocará el TMD. Como unidad de la masa se empleará la tonelada métrica (t) que es aceptada para su uso con unidades del Sistema Internacional y que habitualmente se emplea en esta propiedad de los puentes.
Tabla 1 Parámetros del puente de ferrocarril.
| m1 (t) | k1 (kN/m) | ξ1 | A(kN) | wf (Hz) |
| 95 | 50´000 | 0,025 | 20 | wn |
siendo: m1 la masa; k1 la rigidez; ξ1 la amortiguación; A la amplitud de la fuerza y wf la frecuencia asociada a la fuerza, todos referidos al puente (subíndice 1).
Para calcular los parámetros del TMD se desarrolla un código en el software MatLab 9.12 (R2022a). Se parte de la simplificación de que la estructura cuyas vibraciones se quieren reducir, se comporta como un único grado de libertad y a partir de estos datos iniciales, se crean tres bucles que utilizan un código desarrollado para el modelo de dos grados de libertad. En cada uno de esos tres bucles se modifica uno de los parámetros del TMD manteniendo fijos los otros dos, almacenando los resultados en vectores.
Para ver todo el potencial de amortiguación de estos dispositivos, se va a analizar una estructura cuya excitación provoque la resonancia, o sea, donde la frecuencia provocada por la fuerza perturbadora (wf) coincide con la frecuencia natural de la estructura (w01), que se calcula a través de la ecuación (1):
Masa: Los parámetros utilizados para resolver el problema se muestran en la tabla 2:
Tabla 2 Parámetros para la determinación de la masa.
| m1 (t) | k1 (kN/m) | k2 (kN/m) | ξ1 | ξ2 | A (kN) | wf (Hz) | Amplitud (m) |
|---|---|---|---|---|---|---|---|
| 95 | 50´000 | 4´400 | 0,025 | 0,075 | 20 | 22 | 0,003 |
siendo: k2 la rigidez y ξ2 la amortiguación, ambos del TMD (subíndice 2).
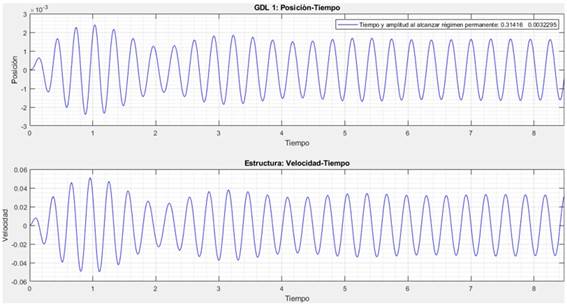
La amplitud de oscilación del puente (0,003) se obtiene del estudio dinámico con un grado de libertad (figura 1).
Utilizando el código de determinación de la masa, se obtiene una gráfica en la que se representan los valores de las amplitudes de la estructura y del TMD, para las distintas masas (figura 2).
La amplitud de la estructura (azul) presenta un mínimo en los desplazamientos para un valor de la masa del TMD (m2) de 8,6 t.
Amortiguamiento: Para disminuir aún más el desplazamiento de la estructura se puede variar el nivel de amortiguamiento. Para ello se realiza un bucle en el programa cuya variable es el amortiguamiento, pero con otros datos de entrada obtenidos en el gráfico anterior como la masa del TMD y la amplitud de la estructura con el TMD sintonizado, estos valores se pueden observar en la tabla 3.
Tabla 3 Parámetros para la determinación del amortiguamiento.
| m1 (t) | m2 (t) | k1 (kN/m) | k2 (kN/m) | ξ1 | A (kN) | wf (Hz) | Amplitud (m) |
|---|---|---|---|---|---|---|---|
| 95 | 8,6 | 50´000 | 4´400 | 0,025 | 20 | 22 | 0,0012 |
siendo: m2 la masa del TMD.
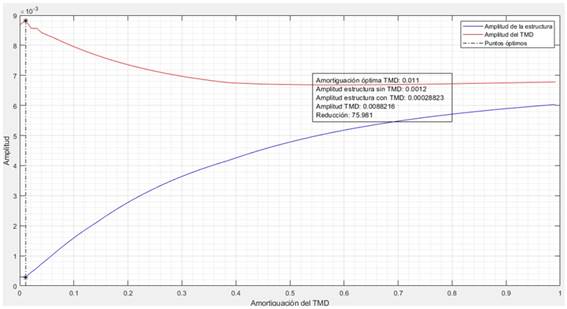
Se ejecuta el código elaborado para optimizar el amortiguamiento y se representa la curva de amplitudes de la estructura y del TMD en función de 𝜉2. Se obtiene la gráfica que aparece representada en la figura 3. El valor óptimo de ξ2 es 0,011.
Rigidez: En la tabla 4, se muestran los datos del problema para determinar la influencia de la rigidez del TMD en el comportamiento de la estructura.
Tabla 4 Parámetros para el análisis de influencia de la rigidez.
| m1(t) | m2(t) | k1(kN/m) | ξ1 | ξ2 | A(kN) | wf (Hz) | Amplitud (m) |
|---|---|---|---|---|---|---|---|
| 95 | 8,6 | 50´000 | 0,025 | 0,075 | 5 | 22 | 0,003 |
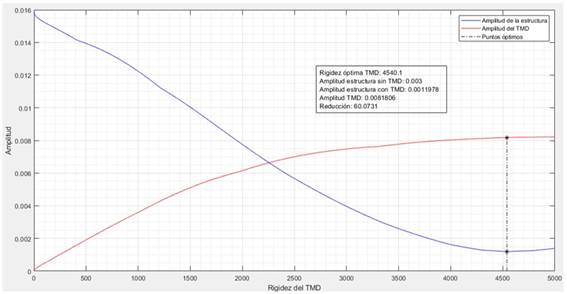
Para minimizar el desplazamiento de la estructura se desarrolla un código similar al de los apartados anteriores, creando un bucle donde se varía la rigidez con los parámetros ya definidos. Se obtiene con ello la gráfica que se muestra en la figura 4. El valor óptimo de k2 es 4´540,1 kN/m. Aquí al igual que en el caso de la masa, la amplitud del desplazamiento de la estructura presenta un mínimo claro para una rigidez determinada.
2.2. Diseño de los principales elementos del TMD. Diseño de los resortes
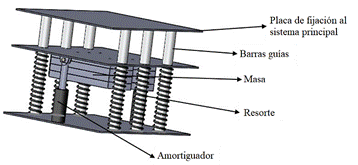
Los principales elementos que componen cualquier modelo de TMD son: resorte, amortiguador y masa oscilante. El resorte, con su rigidez, es el encargado de que se transmita la fuerza de excitación que actúa sobre la estructura y acompaña las oscilaciones de la masa del TMD elásticamente. El amortiguador, con su coeficiente de amortiguamiento, tiene como función absorber la energía del sistema y por ende disminuir las vibraciones. La masa del TMD será responsable de oscilar a la amplitud requerida en la dirección de la vibración (Elias y Matsagar, 2017), (Roozbahan y Turan, 2023). En el epígrafe anterior se calculó que la rigidez adecuada del TMD para la reducción de las vibraciones del sistema principal (k=4´540 kN/m). Esta rigidez es la equivalente para todos los resortes del dispositivo. Para conocer la rigidez de cada resorte se divide la equivalente entre el número de resortes a colocar, ya que estarán posicionados en paralelo. Primero se probó el diseño de los resortes para la colocación de un solo TMD con 3 variantes: TMD con 2 resortes, con 4 resortes y finalmente con 6 resortes, pero de esta manera se obtenía una rigidez muy elevada para los resortes y por tanto sus dimensiones eran erróneas.
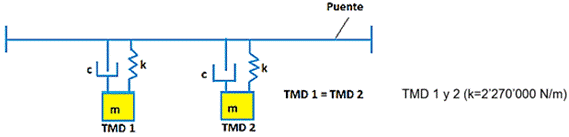
Por las características dinámicas de la estructura y la rigidez del sistema amortiguador obtenidas, se decide colocar dos TMD con las mismas cualidades (figura 5) y se realizará el diseño de los resortes para 4, 6 y 8 resortes en cada TMD (tabla 5).
k=4´540 kN/m k/2TMD=2´270 kN/m * 1´000 N/kN= 2´270´000 N/m (cada TMD)
Tabla 5 Variantes de la cantidad de resortes para dos TMD
| Cantidad de resortes | K para cada resorte (N/m) |
|---|---|
| 4 | 567’500 |
| 6 | 378’300 |
| 8 | 283’750 |
Para realizar el cálculo de los resortes se confeccionó una hoja de cálculo en el software Microsoft Excel 2016 donde se determina el número de espiras activas para cada diámetro de alambre (d) variando el diámetro medio del resorte (D), teniendo en cuenta el material de fabricación y los tres tipos de resortes a diseñar (k1= 567’500 N/m, k2= 378’300 N/m y k3= 283’750 N/m). En la figura 6 se muestra un ejemplo de estas hojas de cálculo.
El material de los resortes será acero al cromo-silicio (UNS G92540; AISI 9254) o acero al cromo-vanadio (UNS G61500; AISI 6150; ASTM 231-41), ambos tienen un módulo de cortante G= 77,2 GPa (77,2e9 N/m2). El diámetro de alambre que se emplea para estos aceros está entre 0.8 y 12 mm. En este diseño se utilizarán diámetros entre 5 y 12 mm.
En la propia hoja de cálculo se grafica la relación entre el número de espiras calculadas (N) y el diámetro medio de la espira (D), para cada diámetro del alambre y cada rigidez del resorte. A modo de ejemplo, en la figura 7 se pueden apreciar estas curvas para la Variante de 8 resortes (k= 283’750 N/m).
2.2.1. Cálculo de las dimensiones y comprobación de la estabilidad del resorte
Se realiza el diseño para tres tipos de resortes (Budynas y Nisbett, 2020):
1. TMD con 4 resortes, o sea cada resorte tendrá una k1= 567’500 N/m.
2. TMD con 6 resortes, cada resorte tendrá una k2= 378’300 N/m.
3. TMD con 8 resorte, cada resorte tendrá una k3= 283’750 N/m.
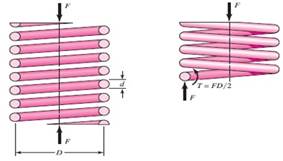
siendo: (figura 8)
d - Diámetro del alambre circular macizo (m).
G - Módulo de Cortante (N/m2).
D - Diámetro medio de la espira (m).
N - Número de espiras activas.
TMD de 4 resortes, k1= 567’500 N/m: De la hoja de cálculo para esta variante, se selecciona un resorte de 11 mm de diámetro del alambre (d), 40 mm de diámetro medio (D) y se calcula el número de espiras activas: N=4.
Dimensionamiento: Los extremos de este resorte de compresión se ponen a escuadra y aplanados a esmeril para obtener una mejor transferencia de la carga. De esto depende los siguientes parámetros geométricos (Budynas y Nisbett, 2020).
d= 11 mm D= 40 mm N= 4
Espiras de extremo, Ne=2.
Espiras totales:
Longitud cerrada (sólida):
Longitud libre:
Paso:
L0, se asume teniendo en cuenta la estabilidad: L0= 200 mm.
Comprobación de la Estabilidad: Los resortes sometidos a altas cargas de compresión pueden perder la estabilidad cuando la deflexión deviene demasiado grande. La estabilidad absoluta, para aceros ocurre cuando:
Para terminales “A escuadra y aplanados” α=0,5 y Lo<5,26*D.
L0= 200 mm; 200 mm < 5,26*40 mm
200 mm < 210,4 mm (Se cumple la Condición de Estabilidad).
Con el mismo procedimiento se realiza el cálculo para las restantes variantes de TMD (6 y 8 resortes). Se obtiene el dimensionamiento de estos resortes y se comprueba el cumplimiento de la condición de estabilidad. En la tabla 6 se resumen las características geométricas de los tres resortes calculados.
2.3. Selección del amortiguador
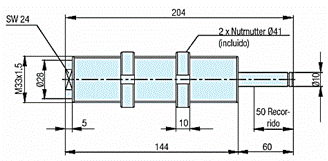
Se realizó una búsqueda bibliográfica encontrándose distintos catálogos de fabricantes de amortiguadores hidráulicos en aplicaciones industriales. De la gran variedad de amortiguadores producidos por diferentes fabricantes, se seleccionó un amortiguador industrial modelo 365M33X1.5LM fabricado en Alemania (ZIMMER, 2023) como se puede apreciar en la figura 9. El mismo se puede integrar perfectamente en el TMD y se sincronizará a la estructura estudiada (puente de ferrocarril). Las dimensiones de este amortiguador se muestran en la figura 10.
Este amortiguador posee un recorrido de 50 mm y resiste una masa efectiva máxima de 2´500 kg. Como la masa que se desplazará sobre el amortiguador en cada TMD es de 4´300 kg, se deben colocar como mínimo 2 amortiguadores en el dispositivo.
2.4. Propuesta de modelo de TMD
Este trabajo no tiene como objetivo el diseño mecánico del amortiguador de masa sintonizado con los detalles técnicos de sus componentes. En este epígrafe solo se pretende hacer una propuesta de TMD modelado en Solidworks 2020 (figura 11), para mostrar una posible disposición de la masa, los amortiguadores y los resortes. Lo que sí queda definido es que el TMD (o los TMD) que se vayan a diseñar para reducir la amplitud de las oscilaciones provocadas por las cargas externas en la estructura estudiada, debe tener los parámetros de rigidez, masa y amortiguamiento calculados en este trabajo.
RESULTADOS Y DISCUSIÓN
3.1. Análisis de los resultados del cálculo de los parámetros del TMD
En el gráfico de la figura 2, se puede observar que el valor de la masa del TMD (m2) de 8,6 t, hace que este tenga una amplitud mucho mayor que la estructura. De esta manera, se aprecia gráficamente que se cumple el objetivo del TMD, ya que la relación entre las variables del problema a la que se llega, hace que el amortiguador absorba gran parte de la energía. Además, se obtienen resultados muy importantes para un estudio dinámico, como la amplitud de la estructura sin TMD y con TMD, observándose una reducción de las oscilaciones de un 58%.
El valor óptimo de ξ2 es 0,011. En la figura 3, se observa que, para la menor amplitud de la estructura, el TMD tiene su mayor desplazamiento posibilitando una reducción en las oscilaciones de un 76%.
El amortiguador C, tiene dos funciones: disminuir las oscilaciones y gastar energía. La rigidez determinada posibilita una reducción de las vibraciones en la estructura de un 60%. Se observa también que para una rigidez del TMD cercana a cero, la amplitud también es casi nula. La rigidez representa la relación entre la fuerza que se aplica a un grado de libertad y el movimiento del mismo (k=F/x). Por lo tanto, si la rigidez es muy alta: el primer grado de libertad (estructura) vibra y transmite una fuerza al segundo. La elevada rigidez impide que el resorte se contraiga, por lo que el segundo grado de libertad (TMD) se desplaza de la misma manera que el primero. Si la rigidez es muy baja: el primer grado de libertad se mueve, pero el resorte apenas se opone a ser comprimido, por lo que el segundo grado de libertad permanece prácticamente inmóvil. Los resortes acompañan las oscilaciones de la masa del TMD elásticamente. Si no existiera amortiguador, los resortes y la masa acompañarían las oscilaciones de la estructura primaria (puente).
3.2. Análisis del cálculo de los resortes
En la hoja de cálculo creada se determinó el número de espiras activas para las tres variantes descritas lo cual posibilitó el dimensionamiento de los resortes. Además, se graficó la relación entre el número de espiras calculadas y el diámetro medio de la espira, para cada diámetro del alambre y cada rigidez del resorte. A partir de estas curvas, se obtiene una familia de ecuaciones que permiten determinar el número de espiras activas en los resortes para cualquier diámetro medio que se desee, teniendo como dato el diámetro del alambre, el material de fabricación y la constante de rigidez del resorte. En tabla 7 se muestran estas ecuaciones para las tres variantes estudiadas.
Tabla 7 Familia de ecuaciones para determinar el número de espiras activas
| Diámetro del alambre D (mm) | Rigidez k (N/m) | ||
| 567’500 | 378’300 | 283’750 | |
| Ecuaciones | |||
| 5 | y = 0,4923x-1,759 | y = 0,7386x-1,759 | y = 0,9847x-1,759 |
| 6 | y = 1,0209x-1,759 | y =1,5315x-1,759 | y = 2,0419x-1,759 |
| 7 | y = 1,8914x-1,759 | y = 2,8374x-1,759 | y = 3,7828x-1,759 |
| 8 | y = 3,2267x-1,759 | y = 4,8404x-1,759 | y = 6,4533x-1,759 |
| 9 | y = 5,1685x-1,759 | y = 7,7534x-1,759 | y = 10,337x-1,759 |
| 10 | y = 7,8776x-1,759 | y = 11,817x-1,759 | y = 15,755x-1,759 |
| 11 | y = 11,534x-1,759 | y = 17,302x-1,759 | y = 23,067x-1,759 |
| 12 | y = 16,335x-1,759 | y = 24,505x-1,759 | y = 32,67x-1,759 |
| Factor de corrección R²: | 0,9851 | 0,9851 | 0,9851 |
CONCLUSIONES
Los parámetros dinámicos del TMD para satisfacer las solicitudes estructurales del puente ferroviario ubicado en el km 560 del Ferrocarril Central son: m=8,6 t, ξ=0,011 y k=4´540 kN/m. Estos parámetros reducen la respuesta dinámica de la estructura en un 58, 76 y 60%, respectivamente cada uno.
La rigidez obtenida, k=4´540 kN/m, es muy elevada para un solo amortiguador de masa sintonizado. Al distribuir esta rigidez en 2 TMD y valorar para cada TMD la colocación de 4, 6 y 8 resortes en paralelo como distintas variantes de diseño, se obtienen resortes con rigideces menores (en el rango real). Para resortes con el mismo diámetro del alambre y de la espira, mientras menor sea su rigidez, mayor será el número de espiras activas y totales del resorte.
La poca complejidad de los elementos que componen un TMD (masa, resortes, amortiguadores y otros accesorios para el ensamblaje y conexión del dispositivo), y la eficiencia, más que probada a nivel mundial, que poseen los TMD, indican la factibilidad de la implementación de estos aparatos, para controlar el fenómeno de las vibraciones en diversos tipos de estructuras, especialmente en los puentes de ferrocarril.