Meu SciELO
Serviços Personalizados
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares em
SciELO
Similares em
SciELO
Compartilhar
Revista Cubana de Química
versão On-line ISSN 2224-5421
Rev Cub Quim vol.26 no.1 Santiago de Cuba jan.-abr. 2014
ARTICULOS
El análisis de sensibilidad de las constantes cinéticas de un mecanismo como una herramienta para elucidar la fenomenología química de una reacción
Sensitivity Analysis of the Kinetics Constants of a Mechanism as a Tool to Elucidate the Phenomenology of a Chemical Reaction
Dr.C. Jurgen Lange-BregadoI, Dr.C. Natalia DavidenkoI, Dr.C. Jacques Rieumont-BrionesII
I. Centro de Biomateriales, Departamento de Química Macromolecular, Universidad de La Habana, Ciudad de La Habana, Cuba, jurgen@biomat.uh.cu, natdavidenko@yahoo.es.
II. Instituto de Ciencia y Tecnología de Materiales, Universidad de La Habana, Ciudad de La Habana, Cuba, jacques@fq.uh.cu
RESUMEN
El análisis de sensibilidad es una herramienta matemática que permite obtener un criterio cuantitativo de cuáles son los pasos elementales que no contribuyen de forma significativa en un mecanismo cinético propuesto. De esta manera, es posible simplificar de manera notable un mecanismo cinético propuesto, y apreciar la influencia que tienen los parámetros en la respuesta del modelo matemático. En este análisis, la aplicación de la metodología de Come permite clasificar los pasos elementales de un mecanismo en tres categorías: 1) despreciables, 2) no determinantes y 3) determinantes. Los resultados obtenidos con esta herramienta en la modelación de los datos experimentales de la fotopolimerización radicálica del metacrilato de furfurilo demuestra que el mecanismo cinético consta esencialmente de los siguientes pasos elementales: Iniciación primaria, transferencia degradativas (Intermolecular y primaria), reiniciación y terminación cruzada.
Palabras clave: modelación matemática, polimerización, estudio cinético, análisis de sensibilidad.
ABSTRACTS
Sensitivity analysis is a mathematical tool that allows to obtain a quantitative criterion of which elementary steps do not contribute considerably to the proposed reaction mechanism. In this way, it is possible to be notably simplified a complex kinetic mechanism, and also, to appreciate the influence of parameters (between them kinetics constants) on the model answer. In this analysis, the application of Come’s methodology permits to classify the elementary steps of a mechanism in three category: Non-sensible, Non-determinant, Sensible. The results obtained with this tool in modeling of experimental data in free radical polymerization of furfuryl methacrylate suggest that kinetic mechanism consists mainly of five elementary steps: 1) primary initiation, 2) propagation, 3) degradative transfers (which include intermolecular and primary), 4) re-initiation and 5) cross-termination.
Keywords: mathematical modeling, numerical integration, furfuryl metacrylate, kinetic study.
INTRODUCCIÓN
El desarrollo de las técnicas de cómputo para la resolución numérica de sistemas de ecuaciones diferenciales (SEDO)1 posibilita actualmente la simulación de los datos experimentales de concentración de las especies en un sistema de reacción química.
El estudio cinético por modelación matemática se puede abordar considerando un esquema o mecanismo cinético que incluya todos los posibles pasos elementales que dan lugar al producto de reacción. En esta tarea, el balance material de cada especie propuesta en este mecanismo utilizando la ley de acción de masas conlleva a la obtención de un SEDO no lineal, en el que cada ecuación diferencial representa la velocidad de formación de cada una de las especies representada en el mecanismo cinético.
Con el objetivo de obtener de este SEDO, la evolución (o perfil de concentración) en el tiempo de cada especie, es necesario utilizar las métodos de integración numérica de SEDO. Estos métodos están bien establecidos en la literatura y existen paquetes de software que pueden ser aplicados a la integración de diferentes tipo de SEDO, como por ejemplo SEDO rígidos (stiff) y no rígidos (non-stiff)2, 3.
En la tarea de modelación matemática, el análisis de sensibilidad constituye una herramienta matemática auxiliar que permite obtener un criterio cuantitativo de cuáles son los pasos elementales que no contribuyen de forma significativa en el esquema cinético propuesto. Así, es posible simplificar de manera notable un mecanismo complejo, y a su vez ganar conocimiento de la influencia de cada paso elemental dentro de la fenomenología de reacción4, 5.
Desde el punto de vista práctico, el análisis de sensibilidad puede ser llevado a cabo por el método directo6, por análisis de Fourier7 o el método de la función de Green8. La utilización de los dos últimos métodos se justifica cuando se tienen mecanismos de cientos de pasos elementales9.
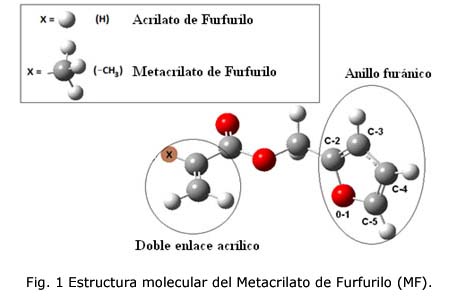
En este trabajo se presentará la implementación de esta herramienta utilizando el método directo y se aplicará a un sistema que posee complicaciones cinéticas tal como la polimerización radicálica en masa del metacrilato de furfurilo (MF, figura 1) en condiciones de iniciación fotoquímica.
FUNDAMENTACIÓN TEÓRICA
El balance material de las especies en un esquema cinético tomando en cuenta la ley de acción de masas, permite obtener un SEDO de primer orden no lineal. Este SEDO puede representarse en forma compacta como sigue:
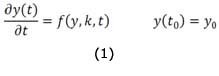
donde y es el vector de las variables dependientes (por ejemplo concentraciones de las especies en el mecanismo) con longitud n; k es el vector de parámetros (constantes cinéticas de los pasos elementales) con longitud m; t es la variable de integración (tiempo) y yo es el vector de condiciones iniciales (concentración de las especies a t = 0).
La diferenciación de la ecuación (1) con respecto a los parámetros k da la siguiente ecuación de sensibilidad10:
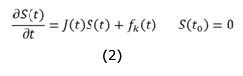
donde S(t) es la matriz n x m de los coeficientes de sensibilidad:
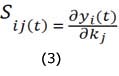
J(t) y fk(t) matriz jacobiana y de derivadas parámetricas respectivamente10. La ecuación (3) puede describirse en forma normalizada en la siguiente manera:
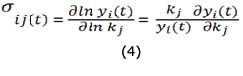
Aplicando aproximaciones de diferencias finitas a la ecuación (4) se obtiene:
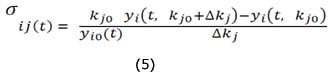
donde ?kj es la variación del parámetro kj(kjf-kjo); kjo es el parámetro kj con valor igual al obtenido en el óptimo, y kjf es un valor asignado al parámetro kj (por ejemplo akjo, siendo a un valor arbitrario). yi(t,kjo + ?kj) es el valor resultante de yi por integración numérica del SEDO con el parámetro modificado k i(kjo + ?kj) a un tiempo dado de reacción.
Desde el punto de vista computacional, la técnica comienza a funcionar, asignando inicialmente a las constantes cinéticas (kjo; j = 1,...,m) los valores obtenidos del conjunto "óptimo" (valores de constantes cinéticas que mejor simulan los datos experimentales). A partir de j= 1 hasta m se van seleccionando y modificando en a veces el valor de la constante . El valor modificado se almacena como kjo, y se realiza la integración del SEDO con esta constante modificada y las demás sin modificar. Con las concentraciones de las especies calculadas (yi) se forma una matriz cuyos elementos sij se obtienen a partir de la ecuación (5). Cada sij informa la variación relativa de la concentración de la especie i debido a la variación relativa de la constante kj.
Es importante mencionar que la matriz de sensibilidad se computa para un determinado instante de tiempo, ya que las concentraciones de las especies que forman esta matriz (y1, y2, y3, ...) se refieren a un instante de tiempo dado; por ejemplo, para un sistema de 50 pasos elementales de reacción y 100 especies, en este caso existe la siguiente matriz de sensibilidad:
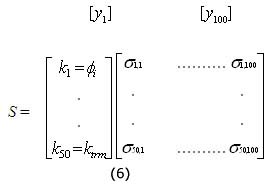
De acuerdo con la metodología de Come4, 5, según los valores escogidos para a y los valores obtenidos de los elementos de la matriz S (sij) se tendrá un juicio de la sensibilidad de los parámetros del sistema. Por ejemplo, cuando a se iguala a 0, y se obtiene como resultado que los coeficientes de sensibilidad sij para un j dado (correspondiente a una fila de la matriz anterior) son menores que 0,01.
Se puede concluir que el paso elemental denotado con kj es despreciable (no sensible), y por tanto puede ser eliminado del mecanismo. Si se calculan los coeficientes de sensibilidad para los pasos elementales restantes haciendo igual a 10 o 0,1, y los coeficientes |sij|, tienen valores muy pequeños, pero mayores que 0,01, tales pasos serán llamados no-determinantes, ya que variaciones limitadas de las constantes cinéticas de los pasos no determinantes no inducen variaciones significativas en las concentraciones de las especies químicas. Por otra parte, si al menos un coeficiente |sij| es aproximado a 1, el paso elemental denotado con kj es llamado determinante ya que variaciones del parámetro (kj) induce variación en al menos una concentración de las especies del sistema.
De lo anteriormente dicho, se desprende que valores precisos de los parámetros despreciables o no determinantes no son necesarios para lograr un buen ajuste del modelo teórico a los resultados experimentales. Desde el punto de vista matemático, esto quiere decir que la variación de los parámetros despreciables o no determinantes en el sistema no tienen influencia significativa en la solución del SEDO, y en términos estadísticos, que la constante cinética posee un intervalo amplio de confianza en la estimación de su valor por modelación11.
Para llevar a cabo un análisis más riguroso de la sensibilidad de las constantes cinética debe efectuarse una cinética de la sensibilidad de las constantes ya que los pasos elementales pueden variar su influencia con el tiempo de reacción. El análisis cinético de la importancia de cada paso elemental que sea no determinante o determinante en el tiempo se puede realizar cuando se grafican los valores de 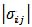 (sumatoria a través de las columnas, siendo n: número de especies) versus tiempo a partir de la información que brindan las matrices de sensibilidad obtenidas a diferentes tiempos de la polimerización.
(sumatoria a través de las columnas, siendo n: número de especies) versus tiempo a partir de la información que brindan las matrices de sensibilidad obtenidas a diferentes tiempos de la polimerización.
Experimento
El avance del proceso de fotopolimerización del MF fue registrado a través de mediciones del calor desprendido en la reacción a diferentes tiempos, para lo cual se empleó un Fotocalorímetro Diferencial de Barrido, basado en la incorporación de un sistema de irradiación a un calorímetro diferencial de última generación, Perkin-Elmer DSC-7 mediante el empleo de fibras ópticas de alta transmisión en el ultravioleta y visible. Antes de comenzar el estudio fotoquímico fue demostrado que en ausencia de irradiación a temperaturas hasta de 40 °C no se detecta polimerización térmica del MF.
La intensidad de luz incidente fue determinada inmediatamente antes de cada experiencia, con una cápsula grafitada idéntica a la que se iba a utilizar para la irradiación de la muestra. Las experiencias se realizaron en atmósfera inerte para lo cual la muestra se mantenía durante 10 minutos antes de iniciar la irradiación en corriente de nitrógeno (caudal estándar= 20 cm3/min). La descripción detallada del equipo, se presentan en el trabajo12.
El fotocalorímetro antes descrito permite determinar la velocidad de desprendimiento de calor (dH/dt) en mcal/s frente al tiempo de irradiación (t) en minutos en forma de una exoterma. Mediante integración de esta curva (cálculo del área bajo la curva a cada tiempo t escogido), se obtiene el calor de polimerización parcial (DHparcial) en cada instante de tiempo t. Con esta magnitud y el calor total de polimerización (DHtotal) se obtiene la conversión (x) de monómero al tiempo t.
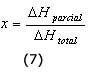
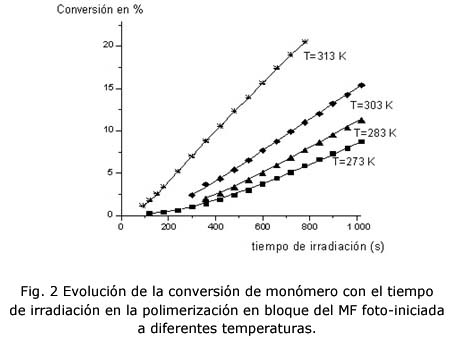
Con la metodología antes descrita se obtuvieron la cinética de polimerización (x vs t, figura 2) del MF a diferentes temperaturas de polimerización (273, 283, 303, 313 K).
Simulación
En la modelación de los datos experimentales de conversión de monómero del MF se utilizó para la integración numérica del SEDO, la rutina de Runge-Kutta implícito de 5to orden con rigidez1, 13. La optimización de los parámetros o constantes cinéticas se llevó a cabo con la rutina NLSFIT13. El análisis de sensibilidad se realizó mediante un programa implementado en FORTRAN 77 MS que usa la rutina de GEAR14, 15 para la integración del SEDO.
d[R·]/dt= 2fiIa - kin [R·][M] - ktp1[A·][R·] - ktp2[F·][R·] - k’trd [R·][M] (8)
d[A·]/dt=kin[R·][M] + kis [F·][M] - 2 kt [A·]2 - ktp1[A·][R·] - ktrd1[A·][M] - ktc [F·][A·] (9)
d[F·]/dt= ktrd1[A·][M] - ktp2[F·][R] - kis [F·][M] - ktc [F·][A·] (10)
-[M]odx/dt=d[M]/dt=-kin[R·][M]-kp[A·][M]-ktrd1[A·][M]-k’trd[R·][M]-ktrm[A·][M]-kis[F·][M] (11)
RESULTADOS Y DISCUSIÓN
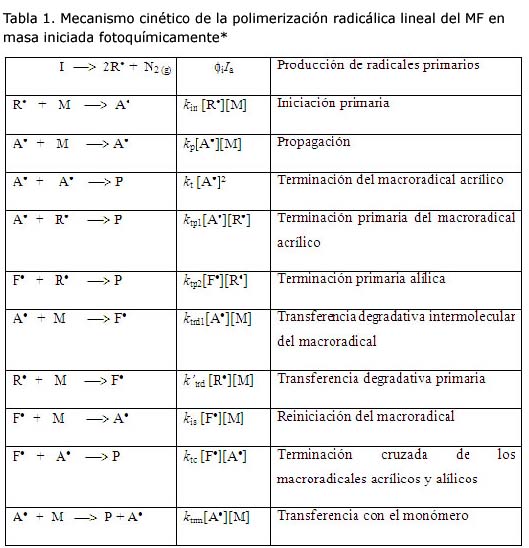
Tomando en cuenta las posibles reacciones que puede tener los dos centros de reacción presentes en el MF (doble enlace acrílico y anillo furánico, ver figura 1) con los radicales se puede proponer un mecanismo cinético como el que se muestra en la tabla 1. El balance material de las especies en este mecanismo de acuerdo con la ley de acción de masas conlleva al siguiente SEDO no lineal:
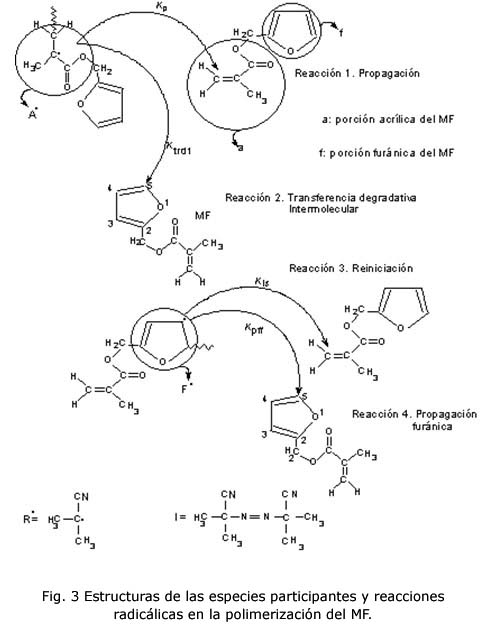
*Las especies químicas (I, R· , A· , F· ) involucradas en la fenomenología de este sistema se presentan en la figura 3
Aquí: [M]o Es la concentración de monómero inicial en la muestra de polimerización (mol . L-1).
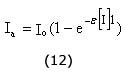
donde:
fi: rendimiento cuántico de iniciación (moles de radicales iniciados (R·) por mol de fotones incidentes);
Ia: intensidad de luz absorbida por el iniciador (Einstein . L-1 . s-1);
e: coeficiente de extinción molar del iniciador (L . mol-1 . cm-1)
[I]: concentración del fotoiniciador (mol . L-1);
l: paso óptico de la luz (cm);
I0: Intensidad de luz incidente sobre la muestra (Einstein/L . s)
[M]: Concentración del MF en la muestra de polimerización (mol . L-1).
A partir de la integración numérica del SEDO [ecuaciones (8) al (11)] y optimización de las constantes cinéticas, se pudo simular exitosamente la conversión de monómero vs tiempo de irradiación a diferentes temperaturas para la fotopolimerización en bloque del MF (figura 2).
Los símbolos indican los valores de conversión de monómero experimentales en por ciento del MF, mientras que las líneas son el resultado de los valores obtenidos por el modelo lineal.
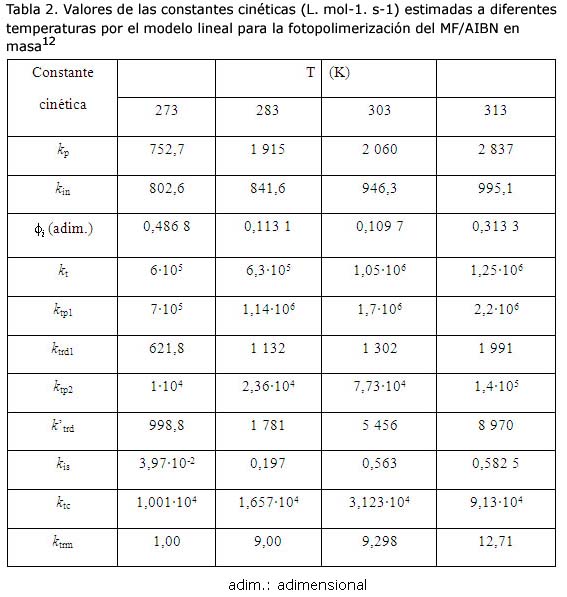
Con las constantes cinéticas optimizadas (tabla 2) se procedió a realizar el análisis de sensibilidad de las mismas con el objetivo de verificar la influencia que tiene cada paso elemental en el mecanismo.
Los resultados obtenidos en este análisis a un tiempo de polimerización igual a 1 380 s se muestran en la tabla 3.
Como se puede apreciar en la tabla 3, los pasos de terminación normal macroacrílica (kt), terminaciones con complicación primaria (ktp1, ktp2) y transferencia con el monómero (ktrm) tienen coeficientes de sensibilidad iguales a cero por lo que se puede concluir que los mismos no son sensibles, y se pueden excluir del esquema cinético.
Por otra parte, como al menos se encuentra un valor de |sij| próximo o mayor a 1 para los pasos de la iniciación (fi, kin), transferencias degradativas (ktrd1, k’trd), reiniciación (kis) y terminación cruzada (ktc), estos son determinantes por lo que deben estar incluidos en el mecanismo.
En el caso particular del paso de propagación (kp), los módulos de los valores de sensibilidad exhibidos en la tabla 3, indican que es un paso no determinante a 1 380 s por tener valores de 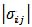 mayores a 0,01 pero no próximos a 1. No obstante este comportamiento no es el mismo al inicio de la polimerización (por ejemplo a los 60 s) en que los valores de sensibilidad obtenidos fueron muy próximos a cero, indicando que este paso se puede eliminar del mecanismo cinético.
mayores a 0,01 pero no próximos a 1. No obstante este comportamiento no es el mismo al inicio de la polimerización (por ejemplo a los 60 s) en que los valores de sensibilidad obtenidos fueron muy próximos a cero, indicando que este paso se puede eliminar del mecanismo cinético.
La explicación a este fenómeno se puede dar si se observa con detenimiento una cinética de sensibilidad de los pasos no despreciables (figura 4). Tal como se puede apreciar de esta figura, el paso de transferencia degradativa intermolecular (ktrd1) tiene los valores más altos de Si=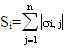 en el sistema desde el mismo comienzo de la polimerización. De acuerdo con el mecanismo propuesto (tabla 1), este hecho sugiere que los pocos radicales A· formados (» 10-7 mol . L-1) en el sistema deben ser consumidos preferentemente por el paso de transferencia degradativa intermolecular para dar lugar a la formación de radicales F· (» 10-4 mol · L-1).
en el sistema desde el mismo comienzo de la polimerización. De acuerdo con el mecanismo propuesto (tabla 1), este hecho sugiere que los pocos radicales A· formados (» 10-7 mol . L-1) en el sistema deben ser consumidos preferentemente por el paso de transferencia degradativa intermolecular para dar lugar a la formación de radicales F· (» 10-4 mol · L-1).
No obstante, a medidas que avanza la polimerización, existe más cantidad de radicales F·, y comienza a favorecerse otro paso por la ley de acción de masas, o sea, el paso de reiniciación radicálica (kis). Este paso conllevaría al incremento de la cantidad de radicales acrílicos A·, y con ello la importancia del paso de propagación (kp), tal como se observa en el incremento de los valores de Si para kp con el tiempo de polimerización (figura 4).
Debido a que la transferencia degradativa intermolecular (ktrd1) es el paso más importante del modelo a cualquier tiempo de polimerización se puede afirmar que la fotopolimerización del MF es un sistema esencialmente autoretardado, ya que en el mismo esta predominando el paso de transferencia degradativa del macroradical metacrílico con el anillo furánico.
Este hecho demuestra que en presencia de anillo furánico en la polimerización de estructuras metacrílicas ocurre una transferencia degradativa por la posición C5 del anillo furánico. Desde un punto de vista de modelación, si este paso de reacción se elimina del esquema cinético, resulta imposible lograr un buen ajuste entre la data teórica y experimental. Esto a su vez, resalta la importancia de esta reacción en el mecanismo. En cambio, al incluir el paso de transferencia degradativa intermolecular en el esquema cinético, se obtienen mediante una rápida convergencia en la optimización, valores adecuados de las constantes cinéticas y se logra también una buena concordancia del modelo a la data experimental.
Los resultados antes expuestos muestran que realmente el mecanismo cinético de polimerización del MF consta esencialmente de 5 pasos relevantes:
1) iniciación (kin), 2) propagación (kp), 3) transferencias degradativas que incluyen la primaria (k’trd) e intermolecular (ktrd1), 4) reiniciación (kis) 5) terminación cruzad (ktc). Considerando estos pasos se pudo modelar también exitosamente la data de polimerización del MF en condiciones de iniciación térmica y de la fotopolimerización del acrilato de furfurilo (figura 1)11 usando el método de los momentos10.
El análisis de sensibilidad de las constantes cinéticas permitió elucidar la fenomenología de polimerización del MF a partir del esclarecimiento de cuáles son los pasos elementales más relevantes de un mecanismo que tiene en cuenta todos los pasos probables.
Se demuestra la importancia del empleo del análisis de sensibilidad tanto para la discriminación de los pasos que no son esenciales en el mecanismo, como para la descripción detallada del aporte de cada etapa elemental a medida que avanza la reacción.
Este análisis, junto a evidencias experimentales cinéticas, se puede usar como una herramienta de verificación de la ocurrencia de pasos elementales en mecanismos químicos.
1. MATRIX LABORATORY (MATLAB R2009a) version 7.8.0347, the MathWorks, Inc. http://www.mathworks.com .
2. KELLS, L. M. Ecuaciones Diferenciales Elementales . 5ª ed. Madrid: Ediciones del Castillo, 1976, 321 p. ISBN 84-219-0288-1.
3. FLETCHER, R. Practical Methods of Optimization. 2da ed. New York: John Wiley & Sons, 2000. UK: Chichester, 436 p. ISBN: 0-471-49463-1.
4. RIEUMONT, J.; VEGA, R. "Studies of the Mechanism of the Radical Polymerization of Vinyl Acetate Inhibited by Furan Compounds. Phenomenology and Sensitivity Analysis". Makromol. Chem. 1991, 192, p. 1387-1397.
5. PIMENTEL, A. S.; GRACIELA, A. "Kinetic Analysis of the Gas-Phase Reactions of Methyl Tert-ButylEther with the OH Radical in the Presence of NOx". J. Braz. Chem. Soc. 1998, 9, p. 539-550.
6. DICKINSON, R. P.; GELINAS, R. J. "Sensitivity Analysis of ordinary differential equation systemsa direct method". J. Comput. Phys. 1976, 21, p. 123- 143.
7. CUKIER, R. I.; SCHAIBLY, J. H.; SHULER, K. E. "Study of the Sensitivity of Coupled Reaction Systems to Uncertainties in Rate Coefficients. III. Analysis of the Approximations". J. Chem. Phys. 1975, 63, p. 1140-1149.
8. MARK, A. K.; RABITZ, H.; CALO, J. M.; KEE, R. J. "Sensitivity Analysis in Chemical Kinetics: Recent Developments and Computational Comparisons". International Journal of Chemical Kinetics . 1984, 16, p. 559-578.
9. EDELSON, D.; ALLARA, D. L. "A Computational Analysis of the Alkane Pyrolysis Mechanism: Sensitivity Analysis of Individual Reaction Steps". International Journal of Chemical Kinetics. 1980, 12, p. 605-621.
10. LANGE, J.; DAVIDENKO, N.; SASTRE, R. "Kinetic Study of the Thermopolymerization of Furfuryl Methacrylate in Bulk by Mathematical Modeling. Part A: Simulation of Experimental Data and Sensitivity Analysis of Kinetic Parameters". Macromol. Theory Simul. 2009, 18, p. 511.
11. LANGE, J.; DAVIDENKO, N.; RIEUMONT, J.; SASTRE, R. "Mathematical Modeling of the Bulk Photopolymeryzatio of Furfuryl Acrylate". Macromol. Theory Simul . 2004, 13, p. 641-654.
12. LANGE, J.; DAVIDENKO, N.; RIEUMONT, J.; SASTRE, R. "Photoinitiated Bulk Polymerization of Furfuryl Methacrylate. Experimental and Kinetic Modelling Results Obtained at Different Temperatures". Polymer. 1998, 39, p. 2537-2542.
13. SCHITTKOWSKY, K. "NLSFIT: Fortran Code for Parameter Estimation in Differential Equation and Explicit model Functions". Mathematisches Institute, Universitat Bayreuth , D' 8580 Bayreuth, Germany.
14. IMSL FORTRAN LIBRARY: The International Mathematical and Statistical Libraries. Reference Manual. Inc. , Houston, 1983.
15. LANGE, J. "Estudio Cinético de la Fotopolimerización del Acrilato y Metacrilato de Furfurilo por Modelación Matemática". Tesis doctoral, Universidad de La Habana, 2007.
Recibido: 15/05/2013
Aceptado: 20/07/2013
Dr.C. Jurgen Lange-Bregado, Centro de Biomateriales, Departamento de Química Macromolecular, Universidad de La Habana, Ciudad de La Habana, Cuba, jurgen@biomat.uh.cu