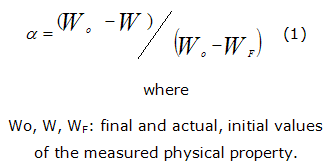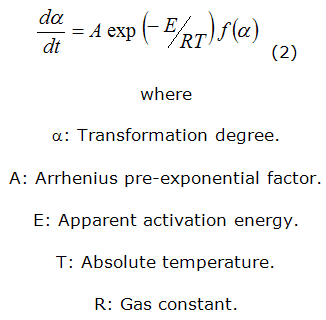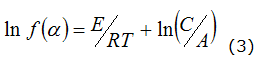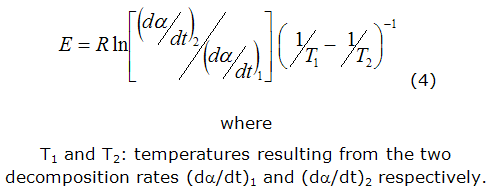Mi SciELO
Servicios Personalizados
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Revista Cubana de Química
versión On-line ISSN 2224-5421
Rev Cub Quim vol.28 no.1 Santiago de Cuba ene.-abr. 2016
ARTICULOS
Análisis Térmico Controlado por la Muestra y Termogravimetría de Alta Resolución. Influencia de las condiciones experimentales sobre los parámetros cinéticos calculados
Sample controlled thermal analysis and high resolution thermogravimetry. Influence of experimental conditions on calculated kinetic parameters
Dra. C. Omaida Quesada-GonzálezI, Dr. Julio Cesar Llópiz-YurellII, Dr. Enelio Torres-TorresII
IFacultad de Ciencias Naturales, Universidad de Oriente, Santiago de Cuba, Cuba, oquesada@cnt.uo.edu.cu
IIInstituto de Ciencia y Tecnología de Materiales, Ciudad de La Habana, Cuba
RESUMEN
El Análisis Térmico Controlado por la Muestra y la Termogravimetría de Alta Resolución fueron empleados para estudiar la deshidratación del BaCl2·2H2O. Los modelos controlados por el avance interfacial bidimensional (R2) y la energía de activación de 26 kJ/mol fueron calculados cuando se aplicaron las técnicas de ATCM; el modelo cinético difusivo tridimensional (D3) y la energía de activación de 40 kJ/mol fueron determinados cuando se aplicó la Termogravimetría de Alta Resolución. Se demostró la influencia de la atmósfera y particularmente de la presión residual en los alrededores de la muestra sobre los parámetros cinéticos calculados.
Palabras clave: Cinética, ATVC, TG Alta Resolución, BaCl2·2H2O.
ABSTRACT
Sample Controlled Thermal Analysis and High-resolution Thermogravimetry are used for to study the dehydration of BaCl2·2H2O. Model controlled by 2-dimensional interfacial advancement (R2) and activation energy of 26 kJ/mol were calculated when the technique SCTA was applied and a 3-dimensional diffusive kinetic model (D3) and activation energy of 40 kJ/mol were determined when Hi- Res ATG was applied. The influence of atmosphere and particularly of the residual pressure in environment of the samples on the calculated kinetic parameters was demonstrated.
Keywords: Kinetics, CRTA, Hi Res ATG, BaCl2·2H2O.
INTRODUCCIÓN
It has often been reported in the literature that the calculated thermoanalytical curves and kinetic parameters in solid state reactions depend on the experimental conditions and it is difficult to accept them as intrinsic constants of the investigated reaction. Many papers have illustrated this problem when the Conventional Thermal Analysis is used. It has been showed the influence of heating rate, sample weight, crystallite size, gas flow and shape of the crucible on the calculated kinetic parameters [1].
In the particular case of the control of atmosphere in environment of the sample, two procedures have been employed:
i) Experiments with permanent vacuum in the reaction zone. The gaseous products are eliminated in a continuous form.
ii) Experiments in dynamic atmosphere. It is used a continuous and constant gaseous flow that carries out the reaction products.
Criado and Rouquerol assert that it is a mistake to suppose that the use of the mentioned procedures (vacuum or flow) is sufficient to depreciate the adverse influence of the atmosphere in environment of the sample. The authors also say that the experimental results may depend on the mentioned conditions [1].
Then, the calculated kinetic parameters by Conventional Thermal Analysis are considered constant of the procedure and operational parameters. These aspects show the vulnerability of obtained kinetic parameters under arbitrary experimental conditions.
It is suggested the effective control of the temperature and pressure gradients, as well as the control of the atmosphere in the environment of the sample to reduce the inconvenience of the influence of the experimental conditions over the calculated kinetic parameters [1].
A new procedure to study the thermal behavior of a substance, based on the control of reaction rate appears. In the decade of 70 this idea was separately developed in Marseilles by Rouquerol and in Budapest by Paulik-Paulik. Rouquerol proposes a new approach known as Constant Decomposition Rate Thermal Analysis (CRTA) and the control of the flow of self-generated gas in the reaction. Paulik´s, in the mean time, suggests other approach known as the Quasi-isothermal and Quasi-isobaric Thermal Analysis (QIQITA) and the control of mass change rate obtained, differentiating electronically the mass signal [2].
In 1989 Rouquerol propose the Controlled Transformation Rate Thermal Analysis (CRTA) with the aim of to give a unified presentation to the modern trends of the Thermal Analysis.
The Controlled Transformation Rate Thermal Analysis can be defined as a general thermoanalytical method where a physical or chemical property X of a substance is modified, following a predetermined program X = f (t) under an appropriate action of temperature [2]. Recently the same author proposed the expression Sample Controlled Thermal Analysis for this same definition [3].
Another technique appears based essentially in the same principle and is known as High Resolution Thermogravimetric Analysis (Hi-Res TGA). In this technique, when no mass loss is occurring, it is possible to have a high heating rate (for example 50 °C/min), but when a minimum loss is detected, the heating rate is reduced towards zero or kept low until the mass again becomes nearly constant [4, 5]. The development of these techniques has allowed a best study of the kinetics parameters in the studied chemical process, what it is evidenced in some paper recently published [6, 7].
However, the effective control of temperature and pressure gradients that these modern techniques offer; sometimes is not sufficient and some researchers report the influence of the experimental conditions on calculated kinetic parameters.
In 1993, Rouquerol studies the kinetic of dehydration of Li2SO4·H2O by CRTA under a residual pressure selected in 10-5–10-2 mbar range. This work shows that, as the controlled pressure is increased, the kinetic model progressively switches from a phase boundary (or first order) controlled type to a nucleation and growth of nuclei [8].
In 1996, Rouquerol using the same technique shows the influence of residual pressure on the kinetic model for the dehydration of uranyl nitrate trihydrate in the range of pressure between 101 and 10-3 mbar. Two kinetic models are distinguished: in the upper pressure region a model of instantaneous nucleation and 2-dimensional nuclei growth occurs, lowering the pressure a 2-dimensional interfacial advancement model is favored [9]. In this paper, we compare the results obtained by Sample Controlled Thermal Analysis (SCTA) and High Resolution Thermogravimetric Analysis (Hi-Res TGA), using as reaction model the first dehydration of BaCl2·2H2O and show the influence of the experimental conditions on calculated kinetic parameters and particularly on the selected kinetic model.
Experimental
Material
In this study was used BaCl2·2H2O Panreac, purity 99 %.
Apparatus
The experiments were all carried out with:
- The thermolysis in SCTA equipment is carried out "under vacuum": The signal is produced by a Pirani gauge, which measures the total residual pressure of produced gases by the thermolysis. This signal is kept constant, controlling the furnace heating via a differential and integral, proportional regulation (PID). With this apparatus it is possible to work under a controlled residual pressure in the intervals from 10-3 to 100 mbar and in the temperature region among 30 and 100 °C. The dehydration of BaCl2·2H2O in a single experiment were carried out under a constant residual pressure of 1,86·10-3 mbar and constant reaction rate C = 0,001 5 h-1. When the rate jumps method is applied the ratio of the rate (rr) is fixed at a value of 4 and the fasted decomposition rate does not exceed 0,02 h-1.
- High Resolution Thermobalance, Hi-Res TGA (TA Instruments, mod. TG-2950). The experiments were done in flow of N2 (100 ml/min). The heating rates were 10 and 20 °C/min in non-isothermal segments and the experimental resolutions used was 5. In all cases the weight sample was about 56 mg.
Kinetic procedure
The kinetic law may be assumed by simple comparing of the experimental curve transformation degree (α) versus Temperature (T), with the set of isokinetic theoretical curves reported by Criado and Ortega. In general, kinetic models of instantaneous nucleation and nuclei growth give rise to curves with a minimum αm. Models limited by diffusion phenomena give rise to curves with an inflexion point (with exception of one-dimensional diffusion), and models governed by interfacial advancement produce curves which show neither a minimum nor an inflexion point [10].
Transformation degree can be calculated by the equation 1:
The analysis of isokinetic data is further carried out in the following way [8, 10] (2):
f (α): Function related to the kinetic model obeyed by the reaction (table 1).
TABLE 1. KINETIC MODEL FUNCTIONS f(α), USUALLY EMPLOYED IN
SOLID STATE REACTIONS [4,10]
| Model | Symbol | f(α) |
| One-dimensional diffusion | D1 | ½ α |
| Two-dimensional diffusion | D2 | -1/ ln (1-α) |
| Three-dimensional diffusion (Jander) | D3 | 3 (1- α) 2/3 / 2 [1-(1-α)1/3] |
| Three- dimensional diffusion (Ginstring- Brounshtein) | D4 | 3/2 [(1-α)-1/3-1]-1 |
| First order | F1 | (1-α) |
| Phase boundary controlled | Rn (1 ≤ n ≤ 3) | n (1-α)1-1/n |
| Nucleation and growth (Avrami-Erofeev) | Am (0,5 ≤ m ≤ 4) | m (1-α)[-ln(1-α)]1-1/m |
If dα/dt is a constant and logarithm is applied and reorganized the equation (2) we obtained the equation (3):
The term ln(A/C) is a constant. Then it is plotted ln f(α) versus reciprocal temperature (1/T) for various functions f(α) and the linear regression coefficients, together with the values of E, are calculated. The kinetic law or kinetic model is obtained from the best regression coefficient and the activation energy is calculated from the slope. This indicates that it is possible to obtain the reaction kinetic parameters from one single experiment [4, 11].
Another way to calculate the activation energy is the following:
When expression (2) is applied for two decomposition rates, in isoconversion points (α1 =α2), it is possible to calculate the activation energy without previous knowledge of the reaction kinetic model [11]. The resulting expression (4) is:
In the particular case of rate jumps method applied in SCTA [8, 9], where the sample decomposes alternatively at two different decomposition rate with a ratio rr, the equation (4) is simplificated to equation 5:
RESULTS AND DISCUSSION
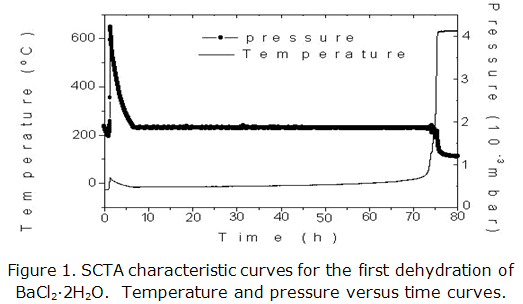
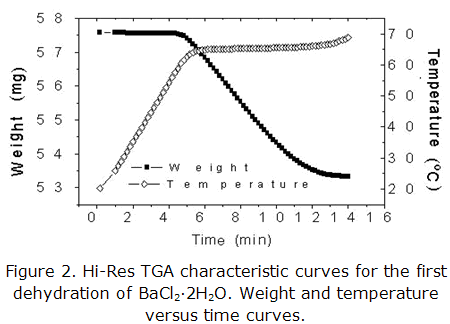
Figures 1 and 2 show characteristic curves of single experiments of SCTA and Hi-Res TGA respectively, for the dehydration first stage of BaCl2·2H2O. In the first case (figure 1) can be observed that reaction occurs under temperature and pressure constant conditions.
In the second case (figure 2) is appreciated an isothermal process. A similar result (isothermal process) is obtained when is applied the Paulik brother technique (QIQITA). These results show the control of temperature and pressure gradients attained with these techniques, which are essential factors to guarantee a best reproducibility and representability of calculated kinetic parameters. These aspects is not attained when are used the techniques of Conventional Thermal Analysis.
Kinetic of the dehydration according to SCTA
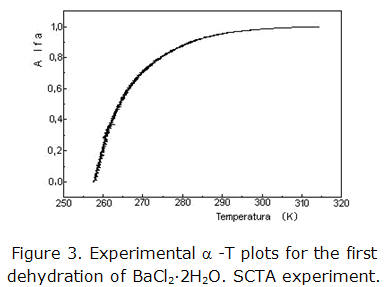
Figure 3 shows the dependency of transformation degree (α) with the temperature, in the interval of 0 ≤ α ≤ 1 for the first dehydration of BaCl2·2H2O. In this case, the single experiments were done under a residual pressure of 1,86 · 10-3 mbar and a constant reaction rate C = 0,015 h-1. This curve has a very interesting feature that offers information about of possible kinetic model of the reaction, when it is compared with the set of isokinetic theoretical curves reported by Criado and Ortega [8, 10]. The profile of this curve suggests that this reaction is controlled by models of interfacial advancement (R2, R3) or first order (F1).
It is obtained a similar result when is applied the expression 3. These results are shown in table 2.
TABLE 2. KINETIC RESULTS OF THE FIRST DEHYDRATION OF BaCl2·2H2O,
FROM EXPRESSION 3 AND SCTA EXPERIMENT
| Symbol of the Kinetic models | Coefficients of Regression | Standard Deviation | Activation Energy kJ/mol) |
| D1 | 0,654 | 0,78 | 42 |
| D3 | 0,890 | 0,79 | 96 |
| D4 | 0,876 | 0,78 | 88 |
| F1 | 0,684 | 0,003 | 7 |
| R2 | 0,992 | 0,061 | 31 |
| R3 | 0,992 | 0,082 | 41 |
| A2 | 0,729 | 0,44 | 59 |
| A3 | 0,461 | 0,57 | 63 |
| A4 | 0,314 | 0,64 | 48 |
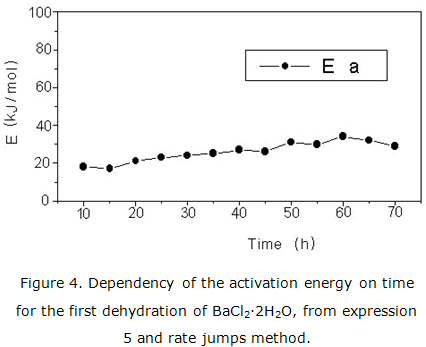
The values of calculated activation energy from this expression are 30 kJ/mol to R2 and 40 kJ/mol to R3. Besides, it is observed that the best fit correspond to the kinetic models R2 y R3; although can be difficult to unambiguously select the correct mechanism. This impossibility of calculation method to discriminate among the models a same group has been frequently reported in literature [1, 8]. Nevertheless, when the rate jumps methods and the equation (5) are applied, it can be identified the correct mechanism. Figure 4 represents the obtained results.
The ratio of the rate (rr) is fixed at a value of 4 and the fasted decomposition rate does not exceed 0,02 h-1.
Thus, the activation energy can be estimated without previous knowledge of actual reaction mechanism. The estimated value is 26 ± 10 kJ/mol. This value is in good agreement with the calculated value to R2 mechanism from expression (3). In this way, can be determined the actual mechanism and kinetic parameters by means of a combination of both analytical results.
Kinetic of the dehydration according to Hi-Res TGA
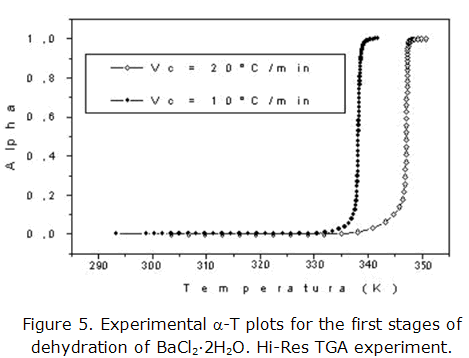
Figure 5 shows the dependency of transformation degree (α) with the temperature, in an interval of 0 ≤ α ≤ 1 and heating rates of 10 and 20 ºC/min, for the first dehydration of BaCl2·2H2O.
When comparing with the set of isokinetic theoretical curves [8, 10] the clearly sigmoide forms of the curves suggests diffusive process. Therefore, the slowest stage in the reaction is the diffusion of the molecules of water through the solid product [12].
Table 3 shows the obtained results to apply the expression 3, when the heating rate is 10 ºC/min. Similar results are obtained for the heating rate of 20 ºC/min. The best adjustments correspond to the kinetics models D1, D2, D3 and D4 although it cannot be select a kinetic model between the diffusive.
TABLE 3. KINETIC RESULTS OF THE FIRST DEHYDRATION OF BaCl2·2H2O
FROM EXPRESSION 3 AND Hi - Res TGA EXPERIMENTS
| Symbol of the Kinetic models | Coefficients of Correlation | Standard Deviation | Activation Energy (kJ/mol) |
| D1 | 0,995 | 0,004 7 | 29 |
| D2 | 0,992 | 0,078 | 14 |
| D3 | 0,986 | 0,128 | 40 |
| D4 | 0,990 | 0,094 | 52 |
| F1 | 0,939 | 0,112 | 96 |
| R2 | 0,939 | 0,056 | 73 |
| R3 | 0,939 | 0,075 | 88 |
| A2 | 0,78 | 0,084 | 23 |
| A3 | 0,797 | 0,077 | 10 |
| A4 | 0,798 | 0,103 | 15 |
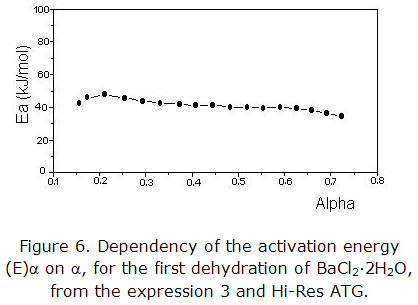
The dependency of the activation energy (E)α on α is shown in the figure 6, when is applied the equation (4) in points of isoconversion, for two experiments done to different decomposition rates.
The figure 6 shows in the 0,13 ≤ α ≤ 0,7 range, that the values of (E)α are essentially constant, with a slight tendency to decrease. Therefore, it is evidenced that activation energy is independent of the transformation degree. The estimated value of activation energy is 40 kJ/mol. The combination of the obtained analytical results from the equations (3) and (4) allows selecting the D3 kinetic model as the most probable, when Hi-Res ATG is used.
General considerations
The most important experimental consideration is deduced when are compared the obtained results by both techniques. In spite of the effective control of temperature and pressure gradients, when are used these experimental procedures, is evident the adverse influence of experimental conditions on the calculated kinetic parameters. The dependency of kinetic parameters and particularly of the kinetic model on the control of atmosphere in immediate vicinity of the sample is demonstrated.
The results suggest the residual pressure as experimental parameter that originates this difference. The experience for SCTA uses lower pressures (vacuum conditions) and a model of interfacial advancement limits the dehydration, while the Hi-Res ATG is carried out to greater pressure and is limited by diffusive process.
The interval of pressures established in each experiment allows favoring one or another kinetic model. In the table 2 for SCTA is observed that, the second models more probable are the diffusives and in the table 3 for Hi- Res ATG, the second models more probable are those characterized by the interfacial advancement.
Rouquerol coincides with Eyraud when asserts, sometimes the vacuum condition eliminate adsorption and diffusion process [13]. This affirmation can explain because during the experience of SCTA, the diffusive process is not determinant.
The literature refers that variations of pressure in 10-5–10-2 mbar range during the study by SCTA of dehydration of the LiSO4·H3O, cause changes of the kinetic model as was referred [8]. It is important to emphasize that the obtained differences in the kinetic models do not alter the values of calculated activation energy from both techniques.
CONCLUSIONS
The influence of atmosphere and particularly of the residual pressure in environment of the samples on the calculated kinetic parameters is demonstrated, for the first dehydration of BaCl2·2H2O. Model controlled by 2-dimensional interfacial advancement (R2) and activation energy of 26 kJ/mol are calculated when is applied the technique SCTA; a 3-dimensional diffusive kinetic model (D3) and activation energy of 40 kJ/mol are determined when Hi- Res ATG is applied. The limited validity of the expression (3) in the discrimination of reaction kinetic model was also demonstrated.
REFERENCES
1. CRIADO, J. M.; ORTEGA, A.; ROUQUÉROL, J. Y.; ROUQUEROL, F., "Un nuevo método de Análisis Térmico: El análisis térmico a velocidad de transformación controlada (ATVC)", Boletín de la Sociedad Española de Cerámica y Vidrio, 1987, 26, 3-11.
2. ROUQUEROL, J., "Controlled transformation rate thermal analysis: the hidden face of thermal analysis", Termochimica Acta, 1989, 144(2), 209-224.
3. ROUQUEROL, J., Sample Controlled Thermal Analysis, 2nd ed., France, Kluwer Acad. Press, 2003, 325 p.
4. HAINES, P. I., Thermal Methods of Analysis. Principles, Applications and Problems, Gran Bretaña, Backie Academic and Professional Publishing, 1995, 132 p.
5. VALOR, A.; KYCIA, S.; TORRES, E.; REGUERA, E.; VÁZQUEZ, C.; SÁNCHEZ, F., "Structural and thermal study of calcium undecanoate", J. Solid State Chemistry, 2003, 172(2), 471-479.
6. TORRES, E.; PELÁIZ, A., "Oxidation kinetic study of copper (I) in ferroelectric ceramic by high resolution thermogravimetric analysis", Thermochimica Acta, 2002, 372(1), 39-44.
7. ALEMAN VÁZQUEZ, L. O.; RODRÍGUEZ GATTORNO, G., "Oxidation process of MoOxCy to MoO3: kinetics and mechanism", J. Solid State Chemistry, 2004, 177(10), 3281-3289.
8. ROUQUÉROL, F.; LAUREIRO, Y.; ROUQUÉROL, J., "Influence of water vapour pressure on the thermal dehydration of lithium sulphate monohydrate", Solid State Ionics, 1993, 63, 363-366.
9. BORDÉRES, S.; ROUQUÉROL, F.; LLEWELLYN, P. L.; ROUQUÉROL, J., "Unexpected effect of pressure on the dehydration kinetics of uranyl nitrate trihydrate: an example of a Smith-Topley effect", Thermochimica Acta, 1996, 282, 1-11.
10. CRIADO, J. M.; ORTEGA, A.; PÉREZ, L., "The use of master plots for discriminating the kinetics model of solid state reactions from a single constant rate thermal analysis (CRTA) experiment", Thermochimica Acta, 1996, 277, 165-173.
11. TADASHI, A.; NOBUYUKI, F., "Controlled-rate thermal analysis. Kinetic study in thermal dehydration of calcium sulphate dihydrate", J. Analytical and Applied Pyrolysis, 1997, 39(2), 129-143.
12. QUESADA, O.; TORRES, E.; LLÓPIZ, J. C., "Termogravimetría de alta resolución. Estudio cinético de la deshidratación térmica del cloruro de bario dihidratado", Revista Cubana de Química, 2002, 14(1), 44-50.
13. ROUQUEROL, J.; GANTEAUME, M. , "Thermolysis under vacuum: essential influence of the residual pressure of thermoanalytical curves and the reaction products", J. Thermal Analysis, 1977, 11(2), 201-210.
Recibido: 07/05/2015
Aceptado: 25/09/2015
Dra. C. Omaida Quesada-González, Facultad de Ciencias Naturales, Universidad de Oriente, Santiago de Cuba, Cuba, oquesada@cnt.uo.edu.cu