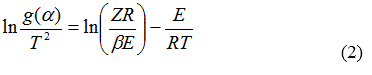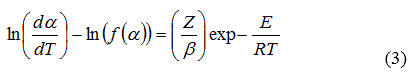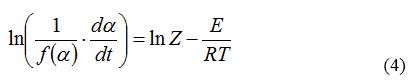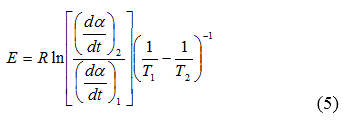Meu SciELO
Serviços Personalizados
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares em
SciELO
Similares em
SciELO
Compartilhar
Revista Cubana de Química
versão On-line ISSN 2224-5421
Rev Cub Quim vol.28 no.2 Santiago de Cuba maio.-ago. 2016
ARTICULOS
Estudio cinético de la pirólisis de la cáscara de naranja
Kinetic study of orange peel pyrolysis
Dra.C. Omaida Quesada-GonzálezI, Lic. Félix Enrique Alfonso-MartínezI, Dr.C. Enilio Torres-GarcíaII
IUniversidad de Oriente, Santiago de Cuba, Cuba, oquesada@uo.edu.cu
IIInstituto de Ciencia y Tecnología de Materiales, Ciudad de la Habana, Cuba
RESUMEN
La pirólisis de la cáscara de naranja es un proceso complejo porque involucra reacciones químicas simultáneas, de ahí la dificultad de realizar un estudio cinético del material. Se utilizaron varias expresiones cinéticas, entre ellas: Coats (integral), Sharp y Achar (diferenciales) e isoconversión (cinética libre). La discusión integrada de los resultados cinéticos logra una mayor representatividad de los mismos, lo cual resulta vital en el tratamiento de materiales naturales. El estudio cinético fue determinado por los modelos D4 y F1. Los valores de la energía de activación calculados se encontraron en un rango entre 80-90 kJ/mol para isoconversión y 25-237 kJ/mol por ajuste de las funciones, lo que se justifica por la ocurrencia de reacciones simultáneas y demuestra la mayor precisión de isoconversión.
Palabras clave: cinética heterogénea, pirólisis, cáscara de naranja.
ABSTRACT
The kinetic study of orange peel pyrolysis is realized in this paper. The pyrolysis is a complex process because it involves simultaneous chemical reactions, thence the difficulty to realize a kinetic study of the material. We use several equations: Coats (integral), Sharp, Achar (differentials) and isoconversional (free kinetic). The discussion integrated of the kinetic results obtains a larger representability of the same, which results necessary in the treatment of natural materials. The study kinetic is determined for models D4 and F1. The rank of activation energy are 80-90 kJ/mol (free kinetic) and 25-237 kJ/mol (model fitting method) because simultaneous reactions occur and demonstrates the biggest precision of the isoconversional method.
Keywords: heterogeneous kinetic, pyrolysis, orange peel.
INTRODUCCIÓN
Los estudios relacionados con la cinética heterogénea en la actualidad pueden ser abordados de diversas maneras. Esta diversidad está sustentada en la variedad de regímenes de calentamiento, métodos, metodologías de cálculo a emplear, equipamiento, material utilizado y particularidades de las reacciones químicas objeto de estudio, lo que ha sido demostrado en los innumerables estudios cinéticos realizados [1,2].
Cuando son aplicados los regímenes de calentamiento no isotérmicos para la realización de los cálculos cinéticos se utilizan dos métodos fundamentalmente: ajuste de las funciones y cinética libre. Dentro del método de ajuste de las funciones existe una gran cantidad de expresiones matemáticas que describen un procedimiento teórico-experimental específico, para llevar a cabo el estudio de una reacción en particular. Estas expresiones matemáticas se dividen en integrales y diferenciales. Además, dentro de este método ha sido muy discutido la influencia sobre los resultados cinéticos alcanzados de las condiciones experimentales de registro de las curvas térmicas, de modo tal que en ocasiones la cinética determinada no es característica de la reacción química en cuestión, sino de las condiciones experimentales, lo que sin duda es una limitación del método [3, 4].
En cuanto al método identificado como cinética libre (isoconversión), su particularidad para determinar la dependencia de la Energía de Activación (Ea) en función del grado de transformación, hacen de esta una técnica eficaz y versátil, muy difundida en la literatura. Esta ventaja se puede convertir en ocasiones en una limitación, por la imposibilidad de determinar el modelo cinético. No obstante, cuando los valores de la Ea calculados por ambos métodos son similares, la combinación de los mismos es una poderosa herramienta para estos estudios [5, 6].
La degradación de la cáscara de naranja, por tratarse de un producto natural, involucra varias reacciones químicas simultáneas. Ellas son la deshidratación del material, degradación de la hemicelulosa, de la celulosa y la lignina [7]. El presente trabajo tiene como objetivo estudiar la cinética de la pirólisis de la cáscara de naranja al utilizar regímenes no isotérmicos de calentamiento que involucran varias velocidades de calentamiento y la combinación de los métodos de ajuste de las funciones y de cinética libre.
MATERIALES Y MÉTODOS
Procedencia de la biomasa
La cáscara de naranja es una biomasa procedente de las jugueras de Veracruz, México. Esta ciudad tiene la mayor producción de cítricos de este país.
Preparación de la biomasa
La cáscara de naranja se secó a temperatura ambiente durante 15 días. Luego se calentó por 24 horas en horno a 120 ºC con flujo de aire. Finalmente, se trituró en un molino de bolas y fue tamizado hasta tamaño de partículas de 0,1 a 0,3 mm. El contenido de humedad determinado por Termogravimetria y fue de 2,7 % a 100 ºC.
Análisis térmico
ATG-CDB
La pirólisis de la cáscara de naranja fue realizada en equipos simultáneos de ATG - CDB (NEZTZSCH STA 409 PC). Se partió de una masa inicial de 12 mg de muestra. La cual fue calentada desde temperatura ambiente hasta 700 ºC a una velocidad de calentamiento de 5 y 10 ºC/min, usando una atmósfera de nitrógeno (100 mL/min).
Metodología
La ecuación básica que define la velocidad de una reacción heterogénea es (1):
Este modelo describe la dependencia de la velocidad de reacción con el grado de avance de la reacción [8, 9] (tabla 1).
TABLA 1. FUNCIONES DIFERENCIALES f (α) E INTEGRALES g(a) MÁS
COMUNES UTILIZADAS EN EL MÉTODO DE AJUSTE DE MODELOS [5]
| Modelo | Símbolo | f(α) | g(α) |
| Difusión unidimensional | D1 | 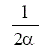 |
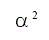 |
|
Difusión bidimensional | D2 | 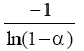 |
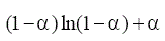 |
|
Difusión tridimensional (Jander) | D3 | 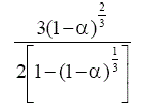 |
 |
|
Difusión tridimensional (Ginstring-Brounshtein) | D4 |  |
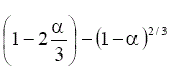 |
|
Crecimeinto unimolecular | F1 |  |
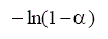 |
|
Fase de frontera controlada | Rn(1≤n≤3) | 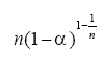 |
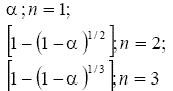 |
|
Nucleación y crecimiento (Avrami-Erofeev) | Am(0.5≤m≤4) | 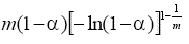 |
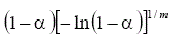 |
En cinética de sistemas heterogéneos, la validez de la ecuación de Arrehenius está asociada a la interpretación física que se le atribuya a los valores experimentales de la energía de activación y el factor pre-exponencial. Se está en presencia de una ecuación de Arrhenius donde la energía de activación está directamente relacionada con la entalpía de activación y el factor pre-exponencial es la frecuencia de vibración de los átomos en la red cristalina [8].
Método de ajuste de las funciones
De forma general, el método se basa en el ajuste por correlación estadística de una serie de modelos matemáticos (diferenciales o integrales) que describen los modelos cinéticos de reacción [1]. Para el estudio cinético se tomaron las ecuaciones de Coats-Redfern (método integral) y las ecuaciones de Sharp y Achar (método diferencial), las que se explican a continuación.
Método de Coats-Redfern
Integrando la ecuación (1) y aproximando la integral de temperatura (la cual no tiene solución exacta) mediante la serie asintótica y tomando hasta el primer término de la serie, al aplicar logaritmos y reordenar, para un programa de calentamiento no isotérmico se tiene la ecuación (2):
Graficando el miembro izquierdo con respecto a 1/T se obtiene E y Z de la pendiente y el intercepto respectivamente. El modelo se obtiene por el mejor ajuste linear [5].
Ecuaciones diferenciales
Estas son más empleadas cuando se puede medir directamente la velocidad del cambio de la propiedad física dα/dt, que al tener solución exacta, brinda más confiabilidad en los resultados [10].
Método de Achar o Método diferencial directo
A partir de reordenar y aplicar logaritmo natural a la ecuación (1) se obtiene la ecuación (3):
Esta ecuación permite obtener los parámetros de Arrhenius (energía de activación y factor pre-exponencial). Al graficar en la ecuación (3) el miembro izquierdo vs. 1000/T para cada función f(α), el modelo cinético que mejor describe la reacción es seleccionado a partir de los valores del coeficiente de regresión (r) y del factor pre-exponencial (Z). Entonces, el valor de la pendiente estará relacionado con el término E/R y el intercepto permite calcular Z [10].
Método de Sharp
En este método no se tiene en cuenta el término de la velocidad de calentamiento (ver ecuación (4)):
Y al graficar el miembro izquierdo vs. 1000/T para cada función f(a) se obtiene el triplete cinético. Debe escogerse entre todos los posibles modelos cinéticos el que tenga un coeficiente de correlación (r) más cercano a 1, así como (Z) que debe estar entre 1011 y 1014 [2].
Método de isoconversión
A este método se le denomina también cinética libre porque permite precisar la dependencia de la energía de activación en función de alfa, sin determinar el modelo cinético que mejor se ajusta a los resultados experimentales.
Para dos series de experimentos en puntos de isoconversión se obtiene la ecuación (5) a partir de la ecuación (1):
Los valores de Ea calculados al aplicar este método de isoconversión o de cinética libre, permiten tener un criterio de mayor fiabilidad que los determinados por el método de ajuste de las funciones f(a); puesto que es posible describir el comportamiento energético durante el curso de la reacción. La combinación de estos métodos puede resultar una herramienta útil en la evaluación cinética de un proceso, lo que facilita su comprensión y disminuye las inconsistencias antes mencionadas [5, 6].
RESULTADOS Y DISCUSIÓN
Estudio cinético de la pirólisis de la cáscara de naranja. Condiciones de registro
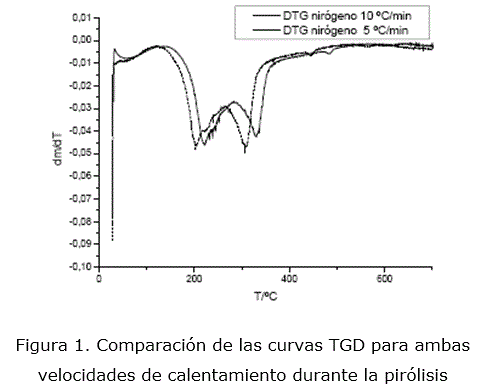
Tal como lo muestran las curvas TGD en la figura 1, el cambio en la velocidad de calentamiento no provoca, de forma general, una variación en el comportamiento térmico de la muestra, en lo que respecta a las etapas de degradación de la cáscara de naranja [7]; no así en cuanto a sus intervalos, los que se desplazan ligeramente, como era de esperarse. Estas similitudes y diferencias argumentan la decisión de estudiar la cinética para cada etapa, considerando que ocurre inicialmente la deshidratación del material, seguido de las etapas de degradación de la hemicelulosa, celulosa y lignina [7]. Es por ello que se presenta a continuación el estudio cinético de cada etapa para ambas velocidades de calentamiento.
Cinética de la Deshidratación del material
La tabla 2 muestra los resultados obtenidos para esta etapa, al aplicar las diferentes ecuaciones por el método de ajuste de las funciones. Se considera hasta Δr = 0.06 para distinguir los modelos más probables, dentro de una misma expresión.
TABLA 2. RESULTADOS CINÉTICOS DE LA DESHIDRATACIÓN EN NITRÓGENO, AL APLICAR
EL MÉTODO DE AJUSTE DE LAS FUNCIONES PARA TRES EXPRESIONES MATEMÁTICAS Y
DOS VELOCIDADES DE CALENTAMIENTO
| Resultados por la Ecuación de Coats | |||||||
| 10 °C/min. Nitrógeno | 5 °C/min. Nitrógeno | ||||||
| Modelo | r | Ea(kJ/mol) | Modelo | r | Ea(kJ/mol) | ||
| F1 | 0,92 | 40 | F1 | 0,93 | 38 | ||
| A2 | 0,89 | 17 | A2 | 0,91 | 16 | ||
| D4 | 0,88 | 69 | D4 | 0,89 | 61 | ||
| R2 | 0,86 | 32 | R2 | 0,87 | 29 | ||
| D2 | 0,86 | 66 | A3 | 0,87 | 9 | ||
| A3 | 0,85 | 9 | D2 | 0,87 | 58 | ||
| R3 | 0,84 | 30 | R3 | 0,85 | 27 | ||
| D1 | 0,83 | 59 | D1 | 0,83 | 51 | ||
| R1 | 0,80 | 27 | A4 | 0,81 | 5 | ||
| A4 | 0,78 | 6 | R1 | 0,80 | 23 | ||
| D3 | 0,05 | 0 | D3 | 0,32 | 1 | ||
| Resultados por la Ecuación de Shart | |||||||
| 10 °C/min. Nitrógeno | 5 °C/min. Nitrógeno | ||||||
| Modelo | r | Ea(kJ/mol) | Modelo | r | Ea(kJ/mol) | ||
| D1 | 0,97 | 41 | F1 | 0,95 | 50 | ||
| D3 | 0,92 | 56 | D4 | 0,93 | 45 | ||
| F1 | 0,89 | 27 | D1 | 0,92 | 275 | ||
| D4 | 0,88 | 51 | F2 | 0,86 | 26 | ||
| R3 | 0,85 | 12 | D2 | 0,83 | 28 | ||
| A4 | 0,82 | 14 | R3 | 0,79 | 12 | ||
| D2 | 0,81 | 37 | F3 | 0,76 | 19 | ||
| F2 | 0,81 | 20 | D3 | 0,65 | 14 | ||
| A3 | 0,77 | 10 | R2 | 0,62 | 5 | ||
| F3 | 0,72 | 16 | A4 | 0,30 | 6 | ||
| R2 | 0,66 | 7 | A2 | 0,24 | 5 | ||
| A2 | 0,36 | 2 | A3 | 0,14 | 3 | ||
| Resultados por la Ecuación de Achart | |||||||
| 10 °C/min. Nitrógeno | 5 °C/min. Nitrógeno | ||||||
| Modelo | r | Ea(kJ/mol) | Modelo | r | Ea(kJ/mol) | ||
| D3 | 0,93 | 54 | D3 | 0,96 | 49 | ||
| D4 | 0,92 | 50 | D4 | 0,95 | 44 | ||
| F1 | 0,87 | 25 | D2 | 0,85 | 27 | ||
| D2 | 0,83 | 36 | F1 | 0,83 | 25 | ||
| R3 | 0,80 | 13 | F2 | 0,70 | 18 | ||
| F2 | 0,77 | 18 | R3 | 0,70 | 11 | ||
| F3 | 0,67 | 14 | F3 | 0,58 | 13 | ||
| R2 | 0,65 | 7 | D1 | 0,51 | 12 | ||
| D1 | 0,64 | 22 | R2 | 0,41 | 4 | ||
| A4 | 0,41 | 9 | A4 | 0,31 | 7 | ||
| A3 | 0,26 | 5 | A2 | 0,18 | 4 | ||
| A2 | 0,15 | 3 | A3 | 0,17 | 4 | ||
Para ß =10 ºC/min, a partir de las expresiones de Coats y Achar se asume que los modelos F1 y D4, se encuentran entre los más probables, con valores de Ea entre 49-68 kJ/mol para D4 y 25-40 kJ/mol para F1. En el caso de la expresión de Sharp, los modelos más probables son el D1 y el D3, estando F1 y D4 entre los que le siguen en probabilidad. Aquí se demuestra lo imprescindible de usar más de una expresión, en aras de lograr resultados más precisos.
Para ß =5 ºC/min al interrelacionar los resultados por las tres expresiones matemáticas, se infiere que los modelos F1 con Ea entre 24-49 kJ/mol y D4 con Ea entre 43-61 kJ/mol son los más probables, lo que coincide con los resultados obtenidos para 10 ºC/min.
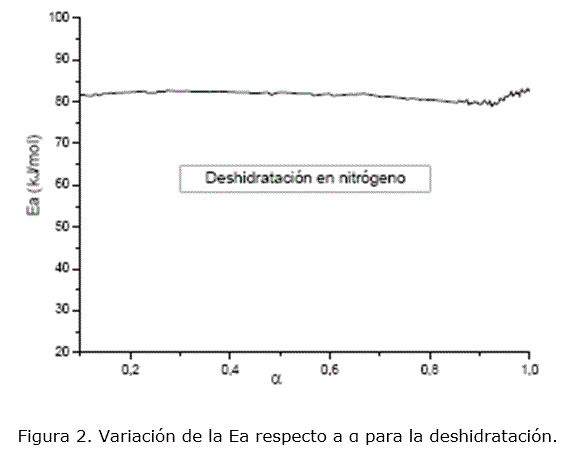
Los valores de Ea calculados por el método de isoconversión (figura 2) se mantienen casi constantes (81-82 kJ/mol) y resultaron próximos a los encontrados para el modelo D4, lo que permite identificar los modelos difusivos como los limitantes durante la deshidratación. Además, los pequeños valores de Ea calculados por todos los métodos y expresiones matemáticas utilizadas, son característicos de procesos difusivos. Por tanto, desde el punto de vista físico la etapa limitante durante la deshidratación es la difusión de las moléculas de agua gaseosa a través de la biomasa sólida.
Cinética de la degradación de la hemicelulosa
Los resultados cinéticos de la pirólisis de la hemicelulosa se muestran en la tabla 3. A diferencia de los resultados obtenidos para la etapa de deshidratación, existe diversidad en el comportamiento cinético para ambas ß, por lo que se discute de manera separada.
TABLA 3. RESULTADOS CINÉTICOS AL APLICAR EL MÉTODO DE AJUSTE DE
LAS FUNCIONES PARA TRES EXPRESIONES MATEMÁTICAS Y DOS VELOCIDADES
DE CALENTAMIENTO, DURANTE LA PIRÓLISIS DE LA HEMICELULOSA
| Resultados por la Ecuación de Coats | |||||
| 10 °C/min. Nitrógeno | 5 °C/min. Nitrógeno | ||||
| Modelo | r | Ea(kJ/mol) | Modelo | r | Ea(kJ/mol) |
| F1 | 0,99 | 84,3 | F1 | 0,98 | 76 |
| A2 | 0,98 | 38,2 | A2 | 0,98 | 34 |
| D4 | 0,98 | 156,8 | D4 | 0,88 | 142 |
| A3 | 0,98 | 22,8 | A3 | 0,97 | 20 |
| R2 | 0,97 | 75,8 | R2 | 0,97 | 69 |
| D2 | 0,97 | 154,5 | D2 | 0,97 | 140 |
| A4 | 0,97 | 15,1 | R3 | 0,97 | 67 |
| R3 | 0,97 | 73,4 | A4 | 0,97 | 13 |
| D1 | 0,96 | 146,3 | D1 | 0,96 | 133 |
| R1 | 0,96 | 69,2 | R1 | 0,96 | 63 |
| D3 | 0,74 | 8,5 | D3 | 0,72 | 7 |
| Resultados por la Ecuación de Shart | |||||
| 10 °C/min. Nitrógeno | 5 °C/min. Nitrógeno | ||||
| Modelo | r | Ea(kJ/mol) | Modelo | r | Ea(kJ/mol) |
| F1 | 1,00 | 69,4 | D3 | 0,99 | 135 |
| F2 | 0,99 | 59,0 | D4 | 0,99 | 131 |
| F3 | 0,99 | 148,9 | R3 | 0,98 | 56 |
| R3 | 0,99 | 60,2 | R2 | 0,98 | 51 |
| D4 | 0,99 | 144,8 | F1 | 0,98 | 68 |
| D3 | 0,98 | 53,8 | D2 | 0,97 | 118 |
| R2 | 0,98 | 55,5 | F2 | 0,97 | 58 |
| D2 | 0,98 | 137,4 | F3 | 0,96 | 53 |
| D1 | 0,92 | 39,5 | D1 | 0,93 | 36 |
| A2 | 0,90 | 22,9 | A2 | 0,83 | 26 |
| A3 | 0,49 | 7,4 | A3 | 0,54 | 12 |
| A4 | 0,02 | 0,3 | A4 | 0,24 | 5 |
| Resultados por la Ecuación de Achart | |||||
| 10 °C/min. Nitrógeno | 5 °C/min. Nitrógeno | ||||
| Modelo | r | Ea(kJ/mol) | Modelo | r | Ea(kJ/mol) |
| D3 | 0,99 | 148 | F1 | 0,99 | 62 |
| D4 | 0,99 | 143 | D3 | 0,99 | 138 |
| R3 | 0,98 | 62 | F2 | 0,99 | 53 |
| F1 | 0,98 | 74 | D4 | 0,99 | 135 |
| R2 | 0,98 | 56 | R3 | 0,99 | 55 |
| D2 | 0,97 | 129 | F3 | 0,98 | 49 |
| F2 | 0,97 | 64 | D2 | 0,98 | 127 |
| F3 | 0,96 | 58 | R2 | 0,98 | 52 |
| D1 | 0,95 | 114 | D1 | 0,97 | 118 |
| A2 | 0,85 | 28 | A2 | 0,87 | 19 |
| A3 | 0,56 | 13 | A3 | 0,36 | 5 |
| A4 | 0,26 | 5 | A4 | 0,15 | 2 |
En el caso de ß =10ºC/min, al comparar los resultados obtenidos para las tres expresiones matemáticas, se observa la similitud entre las r (muy cercanas a uno) para varios de los modelos cinéticos estudiados, lo que no permite distinguir entre ellos. A partir del criterio aplicado, de seleccionar los modelos cinéticos que más se repiten entre los más probables, para las tres expresiones matemáticas estudiadas, se proponen los modelos F1 y D4, con Ea entre 69-84 y 143-157 kJ/mol respectivamente, aunque no excluimos que pudieran coexistir otros modelos.
En el caso de ß =5 ºC/min, se repite la similitud entre los valores de r (muy cercanos a uno) para varios modelos. Vuelve a seleccionarse los modelos F1 y D4 como los más probables a partir del criterio ya expresado en el párrafo anterior; con valores de Ea entre 62-76 y 131-142 kJ/mol, respectivamente. Destacan los elevados valores de Ea calculados por este método para el modelo D4, lo que demuestra la complejidad del proceso que tiene lugar.
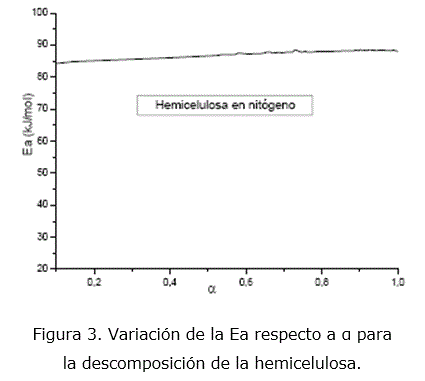
La dependencia de la Ea en función de α, calculada por isoconversión para esta etapa es de 84-87 kJ/mol y se presenta en la figura 3. La mayor similitud entre los valores de Ea calculados para el modelo F1 al emplear ajuste de las funciones y los valores de Ea calculados por isoconversión, constituye un criterio para seleccionar F1 como el más probable. Esto significa, desde el punto de vista físico, que la degradación de la hemicelulosa está determinada por una cinética de primer orden (n=1). En esta etapa aparecen la mayor cantidad de fragmentos orgánicos, lo que indica la depolimerización del material por la acción de la temperatura [7].
Cinética de la degradación de la celulosa
Los resultados obtenidos para la pirólisis de la celulosa se muestran en la tabla 4. Para la ß=10ºC/min se propone D4, por repetirse entre los más probables para las expresiones matemáticas de Coats y de Achar. Los valores de Ea calculados están entre 61-98 kJ/mol. En el caso de la expresión de Sharp, no se toman en cuenta estos resultados por no ser consistentes con los anteriores a partir de los criterios aplicados, si bien los modelos más probables son los difusivos. Se demostrarse nuevamente la validez de la discusión integrada de los cálculos cinéticos.
Para la ß= 5 ºC/min, por primera vez, los modelos cinéticos escogidos a partir del criterio de r para las tres expresiones matemáticas, son diferentes. Resultando como probables, por Coats (F1, A2 y D4), Sharp (D1) y Achar (A4, A3 y A2). Lo anterior no es usual, pues no se esperan que para una misma data se obtengan resultados cinéticos distintos, al utilizar diferentes expresiones matemáticas. De ahí lo imprescindible, cuando se estudian complejos procesos químicos, de utilizar varias expresiones matemáticas. Todo esto provoca cierta incertidumbre en relación al modelo que se propone. No obstante, a partir del criterio ya aplicado de escoger el que más se repite entre los más probables para las tres expresiones matemáticas utilizadas, se propone D4. Los valores de Ea para este modelo están entre 60-103 kJ/mol.
TABLA 4. RESULTADOS CINÉTICOS AL APLICAR EL MÉTODO DE AJUSTE
DE LAS FUNCIONES PARA TRES EXPRESIONES MATEMÁTICAS Y DOS
VELOCIDADES DE CALENTAMIENTO, DURANTE LA PIRÓLISIS DE LA CELULOSA
| Resultados por la Ecuación de Coats | |||||
| 10 °C/min. Nitrógeno | 5 °C/min. Nitrógeno | ||||
| Modelo | r | Ea(kJ/mol) | Modelo | r | Ea(kJ/mol) |
| F1 | 0,89 | 62 | F1 | 0,88 | 66 |
| A2 | 0,85 | 26 | A2 | 0,85 | 28 |
| D4 | 0,83 | 98 | D4 | 0,82 | 103 |
| D2 | 0,81 | 92 | R2 | 0,80 | 48 |
| R2 | 0,81 | 46 | D2 | 0,80 | 97 |
| A3 | 0,78 | 14 | A3 | 0,79 | 15 |
| R3 | 0,78 | 41 | R3 | 0,77 | 44 |
| D1 | 0,77 | 80 | D1 | 0,76 | 84 |
| R1 | 0,72 | 34 | R1 | 0,71 | 37 |
| A4 | 0,68 | 8 | A4 | 0,70 | 9 |
| D3 | 0,45 | 4 | D3 | 0,37 | 3 |
| Resultados por la Ecuación de Shart | |||||
| 10 °C/min. Nitrógeno | 5 °C/min. Nitrógeno | ||||
| Modelo | r | Ea(kJ/mol) | Modelo | r | Ea(kJ/mol) |
| D1 | 0,95 | 93 | D1 | 0,95 | 96 |
| D3 | 0,83 | 64 | D3 | 0,83 | 71 |
| D4 | 0,79 | 56 | D4 | 0,79 | 61 |
| F1 | 0,71 | 24 | F1 | 0,67 | 35 |
| A4 | 0,69 | 32 | D2 | 0,50 | 27 |
| A3 | 0,63 | 25 | F2 | 0,48 | 22 |
| D2 | 0,53 | 29 | A4 | 0,44 | 23 |
| R2 | 0,47 | 11 | A3 | 0,34 | 16 |
| A2 | 0,43 | 13 | F3 | 0,31 | 14 |
| F2 | 0,42 | 11 | R2 | 0,27 | 7 |
| F3 | 0,11 | 3 | R3 | 0,22 | 7 |
| R3 | 0,04 | 1 | A2 | 0,09 | 4 |
| Resultados por la Ecuación de Achart | |||||
| 10 °C/min. Nitrógeno | 5 °C/min. Nitrógeno | ||||
| Modelo | r | Ea(kJ/mol) | Modelo | r | Ea(kJ/mol) |
| D3 | 0,83 | 70 | A4 | 0,89 | 55 |
| D4 | 0,80 | 61 | A3 | 0,88 | 47 |
| F1 | 0,62 | 36 | A2 | 0,84 | 32 |
| D2 | 0,56 | 29 | D3 | 0,75 | 68 |
| F2 | 0,45 | 24 | D4 | 0,71 | 60 |
| A4 | 0,35 | 19 | R2 | 0,67 | 21 |
| F3 | 0,31 | 16 | F3 | 0,55 | 13 |
| R3 | 0,26 | 9 | D2 | 0,49 | 35 |
| A3 | 0,25 | 13 | F1 | 0,48 | 12 |
| R2 | 0,15 | 4 | R3 | 0,40 | 10 |
| D1 | 0,02 | 1 | F2 | 0,16 | 3 |
| A2 | 0,01 | 1 | D1 | 0,14 | 9 |
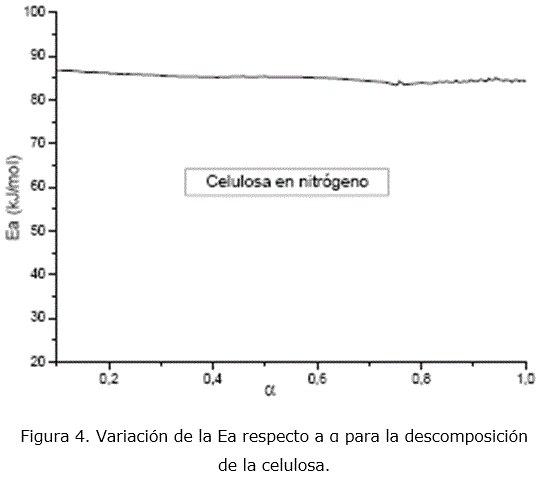
La Ea calculada por el método de isoconversión durante la pirólisis de la celulosa (figura 4), está en el intervalo de 85-87 kJ/mol. Estos valores se encuentran en los intervalos calculados para el modelo D4 por el método de ajuste de las funciones, lo que constituye un criterio adicional para seleccionar este modelo cinético. Al parecer la difusión de los productos gaseosos de la pirolisis de la celulosa (CO2 y H2O) determina la velocidad de la reacción.
Cinética de la degradación de la lignina
Del análisis de los resultados de la tabla 5, para 10 ºC/min se obtiene que los modelos difusivos sean los determinantes, siendo el modelo D4 el más probable, con valores de Ea entre 199-237 kJ/mol. Estos valores son altos para procesos difusivos, por lo que se puede suponer que más de una reacción tiene lugar.
TABLA 5. RESULTADOS CINÉTICOS AL APLICAR EL MÉTODO DE AJUSTE DE LAS FUNCIONES
PARA TRES EXPRESIONES MATEMÁTICAS Y DOS VELOCIDADES DE CALENTAMIENTO,
DURANTE LA PIRÓLISIS DE LA LIGNINA
| Resultados por la Ecuación de Coats | |||||
| 10 °C/min. Nitrógeno | 5 °C/min. Nitrógeno | ||||
| Modelo | r | Ea(kJ/mol) | Modelo | r | Ea(kJ/mol) |
| F1 | 0,96 | 167 | F1 | 0,91 | 165 |
| A2 | 0,95 | 77 | A2 | 0,90 | 76 |
| A3 | 0,94 | 47 | A3 | 0,89 | 47 |
| A4 | 0,93 | 32 | A4 | 0,87 | 32 |
| R2 | 0,91 | 117 | D4 | 0,86 | 259 |
| D4 | 0,91 | 237 | R2 | 0,86 | 127 |
| D2 | 0,89 | 219 | D2 | 0,84 | 245 |
| R3 | 0,88 | 105 | R3 | 0,83 | 118 |
| D1 | 0,85 | 181 | D1 | 0,81 | 215 |
| R1 | 0,83 | 84 | R1 | 0,79 | 101 |
| D3 | 0,15 | 2 | D3 | 0,21 | 4 |
| Resultados por la Ecuación de Shart | |||||
| 10 °C/min. Nitrógeno | 5 °C/min. Nitrógeno | ||||
| Modelo | r | Ea(kJ/mol) | Modelo | r | Ea(kJ/mol) |
| D3 | 0,94 | 226 | D3 | 0,92 | 198 |
| D1 | 0,954 | 173 | D1 | 0,92 | 182 |
| D4 | 0,93 | 199 | D4 | 0,91 | 177 |
| D2 | 0,89 | 104 | D2 | 0,81 | 109 |
| F1 | 0,80 | 156 | F1 | 0,79 | 104 |
| F2 | 0,71 | 124 | F2 | 0,65 | 74 |
| R3 | 0,70 | 79 | R3 | 0,63 | 47 |
| F3 | 0,63 | 101 | F3 | 0,52 | 53 |
| R2 | 0,54 | 41 | R2 | 0,38 | 18 |
| A2 | 0,49 | 69 | A4 | 0,26 | 29 |
| A3 | 0,30 | 39 | A2 | 0,16 | 16 |
| A4 | 0,19 | 24 | A3 | 0,14 | 14 |
| Resultados por la Ecuación de Achart | |||||
| 10 °C/min. Nitrógeno | 5 °C/min. Nitrógeno | ||||
| Modelo | r | Ea(kJ/mol) | Modelo | r | Ea(kJ/mol) |
| D3 | 0,94 | 226 | D3 | 0,92 | 198 |
| D4 | 0,93 | 199 | D4 | 0,91 | 177 |
| D2 | 0,88 | 105 | D2 | 0,81 | 109 |
| F1 | 0,80 | 156 | F1 | 0,79 | 104 |
| F2 | 0,71 | 125 | F2 | 0,65 | 74 |
| R3 | 0,69 | 79 | R3 | 0,64 | 47 |
| F3 | 0,63 | 101 | F3 | 0,52 | 53 |
| R2 | 0,53 | 41 | D1 | 0,48 | 46 |
| A2 | 0,49 | 69 | R2 | 0,38 | 18 |
| D1 | 0,35 | 22 | A4 | 0,26 | 29 |
| A3 | 0,30 | 39 | A2 | 0,16 | 16 |
| A4 | 0,19 | 24 | A3 | 0,14 | 14 |
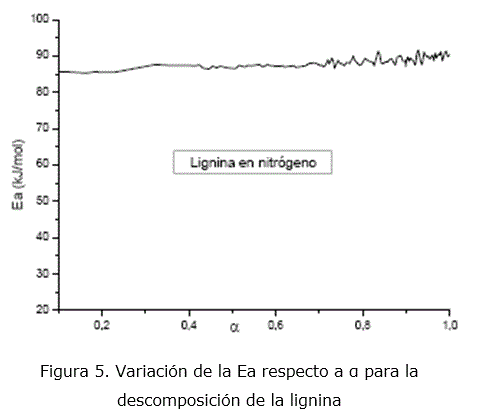
En el caso de 5 ºC/min, se obtiene igualmente el modelo D4 con valores de Ea entre 177-259kJ/mol, significativamente altos para procesos difusivos. Los valores de Ea calculados por el método de isoconversión se muestran en la figura 5. Estos valores son casi constantes dentro del intervalo de 85-90 kJ/mol. Esta es la primera vez que no se observa correspondencia entre los valores de Ea calculados por ambos métodos. No obstante, vuelve a ser la difusión de los productos gaseosos de la degradación de la lignina, los que limitan la velocidad de la reacción, sin excluir la ocurrencia de otros procesos.
A modo de resume en la tabla 6 se presentan los modelos cinéticos y los valores de Ea para ambos métodos y velocidades de calentamientos, durante las 4 etapas. Es evidente que prevalecen los modelos difusivos con excepción de la segunda etapa de degradación de la hemicelulosa, donde el modelo F1 es el que limita la velocidad de la reacción. La similitud entre los modelos cinéticos que predominan para ambas velocidades de calentamiento, permite deducir que esta no influye en la cinética del proceso.
TABLA 6. RESUMEN DE LOS RESULTADOS CINÉTICOS OBTENIDOS PARA AMBAS ATMÓSFERAS,
VELOCIDADES DE CALENTAMIENTO Y MÉTODO DE AJUSTE DE LAS FUNCIONES E ISOCONVERSIÓN
| ETAPAS | Atmósfera de NITRÓGENO (pirólisis) | ||||
| 10 ºC/min. | 5 ºC/min. | Isoconversión | |||
| Modelo | Ea (kJ/mol) | Modelo | Ea (kJ/mol) | ||
| Deshidratación | D4 | 49-68 | D4 | 43-61 | 81-82 |
| Hemicelulosa | F1 | 69-84 | F1 | 62-76 | 84-87 |
| Celulosa | D4 | 61-98 | D4 | 60-103 | 85-87 |
| Lignina | D4 | 199-237 | D4 | 177-256 | 85-90 |
Se demuestra la mayor exactitud del método de isoconversión para el cálculo de la Ea, lo que contrarresta con los valores obtenidos por el método de ajuste de las funciones para algunas etapas. La interrelación de los resultados cinéticos obtenidos a partir de los diferentes métodos y expresiones matemáticas aplicadas, aportó riqueza y precisión al análisis, pues fue demostrada la diversidad de modelos cinéticos que pueden prevalecer cuando se estudian complejas reacciones químicas. Esto constituye una limitación dentro de las investigaciones en esta rama y que la metodología aplicada contribuye a minimizar.
CONCLUSIONES
Se demostró la posibilidad de estudiar la cinética de procesos con reacciones químicas simultáneas, al interrelacionar el método de ajuste de las funciones con cinética libre y varias expresiones matemáticas y velocidades de calentamiento. Las etapas involucradas durante la pirólisis de la cáscara de naranja están limitadas por procesos difusivos con excepción de la degradación de la hemicelulosa que predomina el modelo F1.
REFERENCIAS BIBLIOGRÁFICAS
1. TORRES GARCÍA, E., VALOR, A., KYCIA, S., REGUERA, E., VÁZQUEZ RAMOS, C. y SÁNCHEZ SINENCIO, F., "Structural and thermal study of calcium undecanoate", Journal of Solid State Chemistry, 2003, 172, 471–479.
2. ALEMAN, L. O., TORRES GARCÍA, E., RODRÍGUEZ GATTORNO, G., "Oxidation process of MoOxCy to MoC: kinetics and mechanism", Journal of Solid State Chemistry, 2004, 177, 3281–3289.
3. TORRES GARCÍA, E., PELÁIZ BARRANCO, A., "Influencia de las condiciones experimentales sobre la cinética de deshidratación del K(NbW)O6·H2O", Revista Mexicana de Ingeniería Química, 2003, 2, 83-87.
4. LIU, Y., LIU, A., MAB, B., ZHAO, X., DENGA,Y., ZHANG, H., WANG, Z., "The decomposition of Co(NIA)2 (H2O)4 in nitrogen atmosphere", Thermochimica Acta, 2005, 433, 170–172.
5. KHAWAM A., FLANAGAN, D. R., "Role of isoconversional methods in varying activations energies of solid state kinetics II. Nonissotermal kinetics studies", Termochimica Acta, 2005, 436, 101-112.
6. JANKOVIC, B., "Kinetic analysis of the nonisothermal decomposition of potassium metabisulfite using the model-fitting and isoconversional (model-free) methods", Chemical Engineering Journal, 2007, 30, 12-22.
7. QUESADA GONZÁLEZ, O., TORRES GARCÍA, E., ALFONSO MARTÍNEZ, F. E., "Estudio de la degradación térmica del residuo de la naranja", Revista Cubana de Química, 2011, 23(1), 25-33.
8. GALWEY, A., BROWN, M., "Application of the Arrenius equation to solid state kinetics: can this be justified?", Termochimica Acta, 2002, 386, 91-98.
9. VYAZOVKIN, S. y CHEN, K., "Increase in effective activation energy during physical aging of a glass", Chemical Physics Letters, 2007, 448, 203–207.
10. TORRES, E., BALMASEDA J., CASTILLO, L. F., REGUERA E., "Termal evolution of microporous nitropussides on their dehydration process", Journal of Thermal Analysis and Calorimetry, 2006, 86(2), 371–377.
Recibido: 18/06/2015
Aceptado: 07/01/2016
Dra.C. Omaida Quesada-González, Universidad de Oriente, Santiago de Cuba, Cuba, oquesada@uo.edu.cu