Mi SciELO
Servicios Personalizados
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Revista Cubana de Ciencias Informáticas
versión On-line ISSN 2227-1899
Rev cuba cienc informat vol.7 no.1 La Habana ene.-mar. 2013
ARTÍCULO ORIGINAL
Granada modificado con restricción geométrica
Granada modified with geometric restriction
Daniel Hernández Valdés1, Carlos Enríquez Victorero1, Ulises Jáuregui Haza1*, Pablo Hernández Valdés2, Susana González Santana3
1 Instituto Superior de Ciencias y Tecnología Aplicadas, Quinta de los Molinos, Ave. Salvador Allende y Luaces, Plaza, La Habana, Cuba. *E-mail: ulises@instec.cu
2 Empresa de Consultoría y Seguridad Informática, Calle Zanja, No 651, esq. A Soledad, Centro Habana, La Habana, Cuba
3 Facultad de Química, Universidad de La Habana, Zapata s/n entre G y Carlitos Aguirre, Vedado, Plaza de la Revolución, La Habana, Cuba
RESUMEN
El desarrollo de la química computacional la ha convertido en una sólida e importante disciplina de la química moderna. Numerosos métodos han sido implementados con objetivos muy diversos. La metodología de Hipersuperficie de Múltiples Mínimos permite el estudio de la influencia de disolventes sobre un soluto, y en general de interacciones débiles, haciendo uso de las herramientas de la química cuántica y la termodinámica estadística. Con el objetivo de explorar el espacio de configuraciones se crea un ensemble N, V, T empleando el programa GRANADA para generar celdas o supermoléculas de configuraciones diferentes del (o los) disolvente(s) que rodean al soluto. El programa GRANADA no permite restringir la generación de configuraciones del disolvente a una zona del espacio específica respecto al soluto. Esta restricción es útil para evitar la exploración innecesaria (y el consiguiente costo computacional) de las zonas del espacio que no son de interés o no representan la realidad física del problema. Por tal motivo, en este trabajo se modificó el código fuente del GRANADA para implementar la restricción espacial en la generación de las celdas. Además se presenta un ejemplo de las ventajas de aplicar la restricción para la modelación de la influencia de grupos superficiales en la adsorción de Hexaclorociclohexano en Carbón Activado utilizando un modelo simple.
Palabras clave: GRANADA, hipersuperficie de múltiples mínimos, restricción geométrica.
ABSTRACT
During the last decades the computational chemistry has become more and more a solid and important field of the modern chemistry. Several methods have been developed and implemented to approach several problems. The Multiple Minimum Hypersurfases allows the study of solvent effects and, in general, the study of weak interactions through the use of Quantum Chemistry and Statistical Thermodynamics’ tools. The GRANADA program is used to generate cells or supermolecules of different configurations of the solvent molecules surrounding the solute, to build a canonical ensemble in order to explore the Potential Energy Surface of the system. The GRANADA program doesn't allow constraining the generation of the solvent molecules to a specific area with respect to the solute molecule. This geometric restriction is a useful tool to avoid wasting computational resources exploring space zones with no particular interest or those corresponding with physically unrealistic representations of the system. For that reason, in the present work we modify the GRANADA source code in order to implement the geometric restriction in cells generation. We also present an example of the advantage in applying the restriction for the modeling of Hexachlorocyclohexane adsorption onto Activated Carbon using a very simplified model.
Key words: geometric restriction, GRANADA, multiple minimum hypersurfases.
INTRODUCCIÓN
El desarrollo y evolución de las herramientas y métodos de la química computacional han propiciado un avance importante en la relación teoría-experimento, provocando un progreso acelerado de un gran número de áreas de la ciencia, la tecnología y el medio ambiente. La química computacional abarca un amplio rango de métodos que se diferencian en sus características y aplicaciones principales (Jensen, 1999; Cramer, 2002).La metodología de Hipersuperficie de Múltiples Mínimos (MMH, por sus siglas en inglés; del inglés, Multiple Minimum Hypersurfases) permite, entre sus aplicaciones, evaluar la influencia de disolventes sobre un soluto determinado (Montero, et al., 1998; Codorniu, et al., 2005, Morera, et al., 2009a, b). Para tener en cuenta el efecto de las moléculas de disolvente sobre el sistema en estudio se utiliza una aproximación estadística, se considera un ensemble canónico compuesto por M celdas o supermoléculas de configuraciones diferentes del disolvente rodeando al soluto, a temperatura y volumen constante. Para generar de forma aleatoria estas configuraciones se utiliza un programa escrito en Fortran llamado GRANADA, que está diseñado para leer archivos que contienen las coordenadas atómicas de las moléculas necesarias para crear las celdas (Montero, et al., 1998; Miranda, 2011; Codorniu, et al., 2005; Morera, 2009a).
El GRANADA presenta como inconveniente la imposibilidad de generar celdas en las que las moléculas de disolvente se ubiquen en una zona específica del espacio respecto a la molécula de soluto, lo cual resulta de gran interés para disminuir los costos computacionales o reproducir una realidad física determinada. Por este motivo se hace necesaria la modificación del código fuente del programa con el objetivo de implementar esta prestación.
METODOLOGÍA COMPUTACIONAL
Para poder entender la modificación realizada es necesario primero comprender el algoritmo utilizado por la versión original del GRANADA para generar sus celdas.
Entrada: La entrada del GRANADA consiste en una serie de ficheros con la información de las moléculas de soluto y de los disolventes. Además, un archivo nombrado input (sin extensión) debe estar presente en el directorio predefinido y contiene los parámetros generales para la corrida. En este archivo se define la cantidad y dimensiones de las celdas a crear, el número de moléculas de disolventes entre otras opciones (Montero, 2000; Granada, 2000).
Generación de celdas: El algoritmo utilizado para generar las celdas consiste en encerrar la molécula de soluto en una caja imaginaria la cual es situada en el centro del origen de coordenadas. Posteriormente se generan posiciones y orientaciones aleatorias para las moléculas de disolvente las cuales deben ubicarse entre la molécula central y las dimensiones de la caja cuadrada que se le pasa en el fichero input. Al final de la generación de cada celda se comprueba que no exista superposición de las moléculas. De existir alguna superposición se rechaza la celda y se continúan generando hasta llegar al número orientado.
Salida: La salida de GRANADA consiste en 5 archivos de textos cuyo nombre común es “SOLVATED” con extensiones .MOP cuando se trata de ficheros para emplear con el programa MOPAC en coordenadas internas; .XYZ cuando se trata ficheros a emplear con el programa MOPAC en coordenadas cartesianas; .LOG cuando se trata de los detalles de la formación de cada celda; .CAR cuando se trata del equivalente a .XYZ pero en el formato de archivos .CAR y .INP cuando es el de los detalles implícitos generales a la generación de todas las celdas.
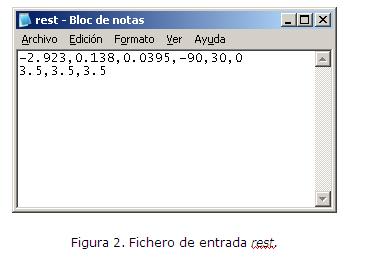
La modificación consiste en poder hacer que el GRANADA genere las celdas ubicando el disolvente en una caja rectangular de dimensiones especificadas por el usuario y que se pueda colocar en cualquier posición respecto a la molécula central (Figura 1). Para esto fue necesario realizar cambios en la entrada de los datos y en la generación de las celdas.
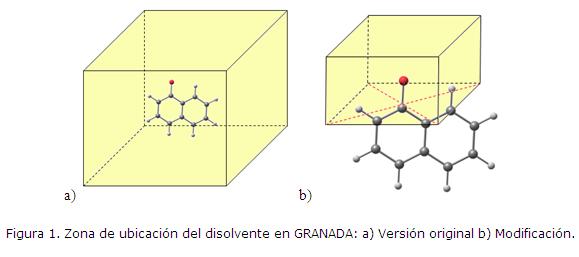
Entrada: Para poder utilizar esta modificación es necesario, además de los archivos de entrada ya mencionados, adicionar un archivo llamado rest como se muestra en la Figura 2. La primera línea contendrá 6 números, todos separados por comas, los tres primeros corresponderán a las coordenadas x, y, z de un punto que servirá de referencia para la creación de la nueva caja donde se ubicará el disolvente. Los otros tres números serán los ángulos a los que hay que rotar la molécula central con respecto a los ejes coordenados para ubicarla en una posición tal que la zona que se desee restringir quede definida en una caja normal al eje z. Los números de la segunda línea corresponden a las dimensiones de la caja, los dos primeros a las semiaristas en x e y, el último, al valor de la arista en z.
La segunda línea es opcional, en caso de no ponerla, las dimensiones de la caja serían las que originalmente se le pasan en el archivo input.
Generación de celdas: El algoritmo empleado en la generación de las celdas varía con respecto a la versión original. Luego de leer la información contenida en los archivos de entrada, las coordenadas del punto de referencia se rotan, los ángulos dados en el fichero rest. A partir de su nueva ubicación se crea la caja donde se va a colocar el disolvente.
Posteriormente, se generan posiciones y orientaciones aleatorias dentro de la nueva caja para las moléculas de disolvente las cuales son rotadas en los mismos ángulos que el punto de referencia pero en sentido contrario. Al final de la generación de cada celda se comprueba que no exista superposición de las moléculas. De existir alguna superposición se rechaza la celda y se continúan generando hasta llegar al número orientado. El algoritmo general se puede ver en la Figura 3.
Salida: Igual que en la versión original del GRANADA.
RESULTADOS Y DISCUSIÓN
Como resultado de esta modificación se tiene un programa que permite generar celdas en las que las moléculas de disolvente se ubican en una zona específica del espacio respecto a la molécula de soluto. Esto resulta de gran interés pues evita la exploración innecesaria (y el consiguiente costo computacional) de las zonas del espacio que no son de interés o no representan la realidad física del problema. A continuación se presenta un ejemplo donde se ilustra cómo la aplicación de la modificación del GRANADA permite obtener mejores resultados.
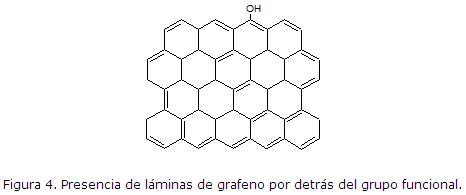
El carbón activado (CA) es un material con una gran área superficial, utilizado debido a su capacidad como adsorbente, para eliminar contaminantes ambientales de soluciones acuosas como son los pesticidas organoclorados. El estudio de la influencia de los diferentes grupos superficiales sobre el proceso de adsorción de los contaminantes puede evaluarse usando un modelo simplificado de carbón activado el cual consiste en un naftaleno con el grupo funcional que se desea evaluar. El uso de este modelo implica que las moléculas de disolvente deben ubicarse solamente en la región del grupo funcional y no por detrás de este donde aparecen láminas de grafeno (Figura 4). Usando la metodología MMH con la restricción geométrica se obtiene una mejor reproducción de la realidad física del fenómeno estudiado respecto al empleo de MMH sin restricción.
Estos resultados se pueden observar al evaluar la adsorción de una molécula de γ hexaclorociclohexano (γ-HCH, pesticida organoclorado) con un grupo hidroxilo (OH) generando 50 celdas. En la tabla 1 se resumen los resultados de las cuatro réplicas realizadas utilizando el MMH con el GRANADA original y la versión modificada. Como se observa, con la versión original en ninguna de las réplicas el número de celdas con sentido físico sobrepasa el 36 % del total, por lo que su utilización provocaría resultados erróneos. Hay que tener en cuenta además, que conocer cuáles de las celdas generadas son útiles para el estudio conlleva a realizar una exploración manual celda a celda, lo cual no es factible para la cantidad de celdas que se necesitan generar en la mayoría de estos estudios. Con la utilización de la modificación del GRANADA el 100 % de las celdas generadas tienen sentido físico (figura 5), lo cual evita una exploración innecesaria de la zona del espacio que no es de interés, disminuyendo así el costo computacional y haciendo más humano el trabajo.
A continuación se muestran los resultados de las energías de asociación obtenidas al evaluar la adsorción de moléculas de agua y de γ-HCH en carbón activado que contienen grupos de superficie hidroxilo y carboxilo. Se comparan los resultados obtenidos utilizando la versión original y modificada del GRANADA con resultados publicados usando cálculos ONIOM DFT/PM3: B3LYP(cc-pVDZ)/B3LYP(6-311++G(2d,2p)) con un núcleo DFT de 3 anillos aromáticos (Collignon, et al., 2005). Como se puede apreciar (Tabla 2) las diferencias de energía entre los cálculos ONIOM y los realizados por nosotros son mayores cuando se emplea el GRANADA original. Además, se puede apreciar que esta diferencia se hace mayor a medida que aumenta el número de moléculas del disolvente. Por su parte, la Tabla 3 muestra la diferencia en los cálculos de energía cuando se estudia la interacción del γ-HCH con CA en ausencia y con la presencia de hasta dos moléculas de agua. Todos estos resultados muestran los beneficios del empleo de esta modificación para el estudio de este tipo de sistemas.
CONCLUSIONES
La modificación realizada al programa GRANADA permite ampliar las utilidades de la metodología MMH para poder restringir la ubicación de las moléculas de disolvente a una zona del espacio respecto al soluto. Aunque la modificación realizada fue motivada por el estudio de adsorción de contaminantes ambientales en carbón activado esta puede ser utilizada en muchos otros sistemas. El empleo de la restricción posibilita la mejor reproducción de la realidad física y la disminución del costo computacional en algunos estudios de interacciones débiles.
REFERENCIAS BIBLIOGRÁFICAS
CODORNIU, E.; MESA, A.; HERNÁNDEZ R.; MONTERO, L. A.; et al. Essential Amino Acids Interacting with Flavonoids: A Theoretical Approach. International Journal of Quantum Chemistry, 2005, p. 103: 82-104.
COLLIGNON, B.; HOANG, P. N. M.; PICAUD, S.; et al. Clustering of Water Molecules on Model Soot Particles: an ab Initio Study. Chem. Phys. Lett., 2005, 1 (4): p. 277-287.
CRAMER, C. J. Essentials of Computational Chemistry: Theories and Models. Chichester, Wiley & Sons, 2002. p. 596.
GRANADA, Manual tutorial para el cálculo de las hipersuperficies de múltiples mínimos. [En línea] 2000. Disponible en: http://karin.fq.uh.cu/mmh/
JENSEN, F. Introduction to Computational Chemistry. Chichester, Wiley & Sons, 1999. p. 429.
MIRANDA, R. A. MMH-2 como una nueva metodología para la predicción de estructuras cristalinas. Tesis presentada en opción al grado científico de Licenciado en Radioquímica, InSTEC. La Habana, 2011. p. 65.
MONTERO, L. A. Manual del usuario GRANADA, 2000.
MONTERO, L. A.; ESTEVA, A. M.; MOLINA, J.; et al. A Theoretical Approach to Analytical Properties of 2, 4-Diamino-5-Phenylthiazole in Water Solution. Tautomerism and Dependence on pH. J. Am. Chem. Soc., 1998, 120 (46): 12023-12033.
MORERA, C.; ALONSO, E.; GONZÁLEZ, R.; et al. A Theoretical Approach to the Solvation of Brassinosteroids. Journal of Molecular Graphics and Modelling, 2009, p. 27: 600-610.
MORERA, C.; MORA N.; MONTERO, L. A.; et al. Interaction of Brassinolide with Essential Amino Acid Residues: A Theoretical Approach. Journal of Molecular Graphics and Modelling, 2009, p. 5931: 1-8.
Recibido: 15/01/2013
Aceptado: 23/01/2013