Mi SciELO
Servicios Personalizados
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Revista Cubana de Ciencias Informáticas
versión On-line ISSN 2227-1899
Rev cuba cienc informat vol.7 no.4 La Habana oct.-dic. 2013
ARTÍCULO ORIGINAL
Métodos de búsqueda para la configuración de redes neuronales asociativas
Methods of search to the configuration of the associative neural nets
Yoan Martínez-López1*, Rafael Falcón Martínez2
1Facultad de Informática. Universidad de Camagüey, Circunvalación Norte, km 5 ½, Camagüey, Cuba. CP.: 74650
2Electrical Engineering & Computer Science (EECS) University of Ottawa 800 King Edward Ave, Ottawa ON Canada K1N 6N5
*Autor para la correspondencia: yoan.martinez@reduc.edu.cu
RESUMEN Dentro del campo de la Inteligencia Artificial, el uso de las redes neuronales, permiten la resolución de problemas complejos. Es por eso que encontrar una configuración de un vector de entrada para trabajar con redes neuronales se hace muy engorroso, por lo cual se hace necesario utilizar métodos de búsquedas eficientes, como son: los métodos de búsquedas heurísticas: ascensión de colinas, búsqueda exhaustiva, algoritmos genéticos (AG), entre otros. El presente artículo consiste en el desarrollo de un diseño para la búsqueda de una configuración del vector de entrada para el trabajo con las redes neuronales asociativas.
Palabras clave: búsqueda, redes neuronales asociativas.
ABSTRACT
Within the field of Artificial Intelligence, the use of neural networks allows complex problem solving. That is why to find a configuration of an input vector to neural networks work becomes very cumbersome, so it is necessary to use efficient searching methods such as heuristic search methods: hill-climbing, exhaustive search, genetic algorithms (GA), among others. This article is the development of a design for finding a configuration of the input vector to the work with the associative neural network.
Key words: Associative neural net, search.
INTRODUCCIÓN
En la solución de problemas complejos de Inteligencia Artificial (IA), unas de las técnicas empleadas son las redes neuronales. Las redes neuronales artificiales (RNAs) son modelos computacionales que pretenden simular el funcionamiento del cerebro humano a partir del desarrollo de una arquitectura que toma las características del funcionamiento de este órgano sin llegar a desarrollar un duplicado del mismo. Las RNAs son capaces de aprender de la experiencia, de extender nuevos ejemplos a partir de ejemplos anteriores, las mismas son utilizadas para la predicción, la minería de datos, el reconocimiento de patrones, los sistemas de control adaptativo, entre otras aplicaciones.
Dentro de los distintos modelos de RNAs, se encuentran, los de tipo asociativo, que han aportado soluciones eficientes a problemas complejos (Bello, 2002), entre los que se destacan Hopfield (Hopfield, 1982), IAC (McClelland 1989), SIAC (García, 1997). La topología de los modelos de RNA asociativas (RNAAs) se forman por un grupo de neuronas por cada atributo del dominio del problema. En cada grupo se coloca una neurona por cada valor que aparezca para ese atributo en el conjunto de datos, existiendo enlaces entre las neuronas de grupos diferentes.
Debido a que la configuración de un vector de entrada para trabajar con redes neuronales se hace muy engorrosa, ya que depende de los diferentes parámetros de entrada, entre los cuales se encuentran las estrategias de asignación de los pesos, el tratamiento de los pesos de las redes, el procesamiento de los rasgos, si se desea configurar manualmente este vector, el espacio de búsqueda que permite obtener el mayor rendimiento de la RNAAs dados los parámetros de entrada se hace muy complejo, por eso es necesario utilizar métodos de búsquedas eficientes.
MATERIALES Y MÉTODOS
El problema consiste en encontrar un vector de configuración, para la obtención de un mayor rendimiento de las redes neuronales asociativas, utilizando un determinado método de búsqueda que a continuación se analizará.
Algoritmos de Búsquedas
Búsqueda exhaustiva o fuerza bruta:
Es una técnica sencilla donde se exploran todas las posibles soluciones del problema, de forma enumerada hasta encontrar una solución que satisfaga el problema, es decir, buscar la mejor una solución a un problema dado de forma secuencial.
Ascensión de colinas (Hill Climbing):
El método de búsqueda conocido por ascensión de colinas es un bucle que se mueve en dirección del valor creciente y termina cuando alcanza un pico en el que ningún vecino tiene valor mejor. A continuación se muestra su algoritmo:
P1. Evaluar el estado inicial. Si es objetivo SALIR con ÉXITO.
P2. Iterar hasta encontrar una solución o hasta que no haya nuevos operadores aplicables al estado actual.
Seleccionar un operador todavía no aplicado al estado actual y aplicarlo para producir un nuevo estado.
Evaluar el nuevo estado.
Si es objetivo SALIR con ÉXITO.
Si es mejor que el estado actual hacerlo estado actual.
Si no es mejor que el actual continuar en el lazo.
Algoritmos Genéticos (AG):
Los Algoritmos Genéticos (Goldberg, 1998), son métodos de búsqueda de propósito general basados en los principios de la genética natural, es decir, son algoritmos de búsqueda basados en los mecanismos de la selección natural y la genética.
Surgen como herramientas para la solución de complejos problemas de búsqueda y optimización, producto del análisis de los sistemas adaptativos en la naturaleza, y como resultado de abstraer la esencia de su funcionamiento. El término Algoritmo Genético se usa por el hecho de que estos simulan los procesos de la evolución a través del uso de operadores genéticos que operan sobre una población de individuos que “evoluciona” de una generación a otra. Los Algoritmos Genéticos son métodos de búsqueda de propósito general basados en los principios de la genética natural, es decir, son algoritmos de búsqueda basados en los mecanismos de la selección natural y la genética. Un AG puede ser visto como una estructura de control que organiza o dirige un conjunto de transformaciones que se ejecutan iterativamente sobre una población de individuos que representan soluciones para el problema a resolver; estas transformaciones se realizan mediante los llamados operadores genéticos, y considerando una función de calidad o grado de aptitud de un individuo, la cual es una medida que permite comparar las soluciones para determinar cuál es mejor.
Optimización basada en mallas variables (VMO):
La cual cae en la categoría de las técnicas de computación evolutiva. Un conjunto de nodos que representan soluciones potenciales de un problema de optimización forma una malla que dinámicamente crece y se desplaza por el espacio de búsqueda, para ello en cada ciclo se generan nodos intermedios entre los nodos de la malla y aquellos nodos que son extremos locales, entre los extremos locales y el extremo global y a partir de los nodos más externos de la malla. Los mejores nodos de la malla resultante son usados como malla inicial para el ciclo siguiente. La intención del nuevo modelo es permitir una mayor exploración del espacio de búsqueda.(Bello, 2007) . Un conjunto de nodos que representan soluciones potenciales de un problema de optimización que forma una malla que dinámicamente crece y se desplaza por el espacio de búsqueda.
Optimización basada en Enjambre de Partículas (PSO):
La optimización basada en enjambre de partículas (Engelbrecht, 2006), es un método de optimización bioinspirado basado en una población. Esta optimización está inspirada en el movimiento de los muchos individuos hacia un objetivo predefinido. El objetivo es maximizar o minimizar la función fijada.
Modelos de Redes Neuronales Artificiales (RNA):
Las RNA no son más que un modelo artificial y simplificado del cerebro humano, que es el ejemplo más perfecto del que disponemos para un sistema que es capaz de adquirir conocimiento a través de la experiencia. Debido a su constitución y a sus fundamentos, las RNA presentan un gran número de características semejantes a las del cerebro.
Dentro del área vasta y compleja de la resolución de problemas, los modelos asociativos han aportado una parte considerable de la eficiencia en la solubilidad lograda a escala mundial por las RNA (Bello, 2002). La topología de los modelos de RNA asociativos se forma por un grupo de neuronas por cada rasgo del dominio del problema. En estos grupos se coloca una neurona por cada valor que aparezca para ese rasgo en el conjunto de datos. Existen enlaces entre las neuronas de grupos diferentes.
Modelos de redes neuronales artificiales asociativas (RNAAs):
Modelo de IAC:
En la topología del modelo de IAC (McClelland, 1989) las neuronas se distribuyen en grupos y se establecen enlaces entre las neuronas de grupos diferentes y del mismo grupo. Las conexiones entre las neuronas de grupos diferentes son excitadoras, mientras que las conexiones dentro de los grupos son inhibitorias.
Este modelo puede ser usado como una memoria asociativa, donde la recuperación de un conjunto de atributos puede ser lograda mediante la estimulación de otros. IAC consiste de un conjunto de unidades de procesamiento organizadas en un número de grupos competitivos (llamados también pools). Hay conexiones bidireccionales inhibidoras (peso < 0) entre las unidades del mismo grupo, y bidireccionales excitadoras (peso > 0) entre neuronas de diferentes grupos. Cada unidad dentro del mismo grupo se conecta a todas las demás, y este es el mecanismo por medio del cual se logra la competencia. La tendencia es que las neuronas con mayor activación en el grupo tienden a someter a las otras, reforzando su propia señal y debilitando la de las demás. Los enlaces entre los grupos también son bidireccionales, lo que significa que un cambio en las unidades de cualquier grupo afectará otros grupos.
La entrada neta se calcula de la siguiente forma:.
Net = weightij*outputi+outputj (1).
Dónde:
weightij: es el peso del enlace entre la unidad i y la unidad j,
outputi: es el valor actual de activación de la neurona i
extinputj: es el valor de cualquier entrada externa a la unidad j.
En el modelo IAC todas las unidades pueden ser unidades de entrada, o sea, pueden ser estimuladas desde el exterior. Y también todas las unidades pueden ser consideradas de salida, pues la activación final de cualquier unidad nos brinda información acerca del comportamiento de un cierto rasgo. Este tipo de red asociativa posee un aprendizaje off line, y los pesos pueden ser positivos o negativos en dependencia del tipo de conexión que se establezca entre dos unidades. Los pesos no cambian con el tiempo, pues se calculan al inicio y no varían como en otros modelos.
Modelo SIAC:
El modelo de SIAC (García, 1997) ofrece cierta igualdad con el IAC, aunque aquí no existe competencia entre las neuronas del mismo grupo.
Las neuronas se organizan, al igual que en el IAC, por grupos, donde cada grupo se corresponde con un rasgo. En cada grupo se sitúa un nodo por cada elemento del dominio del rasgo. Se denomina dominio del rasgo xi y se denota por DOM (xi) al conjunto de valores que toma el rasgo según los elementos del conjunto de entrenamiento. Existe un arco no dirigido entre todo par de nodos, excepto entre los situados en el mismo clúster. Cada arco posee un peso wij que indica en qué medida se relacionan ambos valores. La función de activación de las unidades de este modelo puede describirse así:
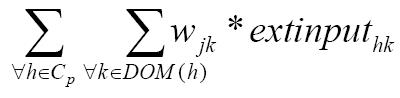 (2)
(2)
Dónde:
Cp: conjunto de rasgos predictores.
Extinput: entrada externa de la neurona representando el h-ésimo valor del rasgo k-ésimo.
Modelo Hopfield:.
Las redes de Hopfield (Hopfield, 1982) son redes de adaptación probabilística, recurrentes, funcionalmente entrarían en la categoría de las memorias autoasociativas, es decir, que aprenden a reconstruir los patrones de entrada que memorizaron durante el entrenamiento.
Una red de Hopfield se compone de sola capa de neuronas), pues recuerda un conjunto de vectores de entrada {x1 , x2 , ... , xN }. La forma en que se determinan los pesos es:
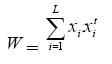 (3)
(3)
Siendo L la cantidad de patrones de entrada a memorizar.
Xi representa el valor de la neurona i.
W el peso total del entrenamiento de la RNA.
Estos modelos de RNA asociativas se encuentran implementados en la herramienta NeuroDeveloper (Falcón, 2003), donde se procesan los atributos de tipo simbólico y numérico. La selección de los valores representativos está guiada por el criterio experto en el dominio de aplicación. NeuroEvaluator (Falcón, 2006), otra plataforma computacional para la evaluación de modelos neuro-borrosos asociativos.
Forma de tratamiento de los pesos.
Todos utilizan un aprendizaje basado en la regla de Hebb, y en particular se definen tres variantes para el cálculo de los pesos: Frecuencia Absoluta, Frecuencia Relativa y Coeficiente de Correlación de Pearson. Con los cuales se calcula la activación de cada neurona.
Estrategia de asignación
Se especifica qué tipo de estrategia se aplicará para las funciones de pertenencia, a la hora de preprocesar los datos:
- Todas las pertenencias.
- Máxima pertenencia.
- Pertenencia>
Preprocesamiento de los rasgos
Para el procesamiento de los rasgos hay que tener en cuenta el tipo de rasgo con el cual trabajará la RNAAs, ya que en dependencia del tipo de rasgo se aplicará la lógica borrosa para fuzzificar el mismo utilizando una determianda función de pertenencia o se discretizará usando un determinado método de discretización.
Lógica borrosa (fuzzy logic):
Según (Östermark, 2000; Zadeh, 1994), la lógica borrosa surge como la posibilidad de flexibilizar el arcaico concepto de que una cosa “o es, o no es”, pues en la mayoría de los problemas de la matemática, estas decisiones duras son inconsecuentes y el principio del tercio exclusivo nos puede llevar a un callejón sin salida ante una decisión en la que exista un por ciento de verdad y otro de falsedad (Falcón, 2006).
Función de pertenencia (FP):.
Si X es una colección de objetos denotados genéricamente por x, entonces un conjunto borroso A en X se define como un conjunto de pares ordenados.
![]() (4)
(4)
Para cada término lingüístico se define un conjunto borroso mediante su función de pertenencia (FP).
Los tipos de FP (Nauck, 1997) más utilizadas dentro de la lógica borrosa son:
- Función de pertenencia triangular.
- Función de pertenencia trapezoidal.
- Función de pertenencia gaussiana.
- Función de pertenencia sigmoidal.
- Función de pertenencia beta.
- Función de pertenencia campana.
Discretizar los rasgos
No es más que dividir los valores de un atributo continuo, en un conjunto de intervalos adyacentes correspondiente al caso unidimensional de los métodos de agrupamiento. Este caso, conocido como discretización, es de especial importancia en Inteligencia Artificial, pues permite que muchos algoritmos de aprendizaje ideados para funcionar con atributos nominales o categóricos puedan también utilizarse con conjuntos de datos que incluyen valores numéricos (Hussain, 1999), algo esencial en la resolución de problemas reales.
En este caso se divide el rasgo en intervalos según el criterio de un experto o utilizando métodos automáticos. La correcta determinación de dichos intervalos se corresponde con el método empleado con este objetivo. Algunos métodos de discretización conocidos son: Equal Width (Hussain, 1999), Equal Frequency (Hussain, 1999), Chi-2 (Liu, 1997), CAIM (Kurgan, 2004), K-Means (Jyh-Shing, 1998).
Vector de configuración
Para el diseño del vector de configuración se debe tener en cuenta lo siguiente:
V = (v1, v2, v3, v4)
Donde:
v1 es el modelo de RNA asociativa.
v2 es la forma de tratamiento de los pesos.
v3 es la estrategia de asignación.
v4 es el preprocesamiento de los rasgos.
Teniendo en cuanta lo siguiente:
De la plataforma NeuroEvaluator:
Para v1: se seleccionan tres modelos de RNAAs.
Para v2: se seleccionan tres formas de tratamiento de los pesos.
Para v3: se seleccionan tres estrategias de asignación.
Para v4: existen AN formas de preprocesar todos los atributos de los que consta la base de casos, donde N es la cantidad de atributo y A las maneras de modelar un atributo.
En resumen el espacio total de búsqueda para encontrar el vector de configuración correspondiente con el objetivo de obtener el mejor rendimiento de la RNAAs será:
Espacio Total de Búsqueda (ETB) = 3*3*3* AN de combinaciones. (5)
Es decir el vector de configuración está formado por A+3 componentes pueden tomar 27* AN valores. La primera componente del vector son los modelos de RNA; se formará un vector por cada modelo fijando en la primera posición el modelo de RNA correspondiente y manteniendo el resto de las posiciones con valores iniciales iguales para todos los vectores que se formen. Estos valores iniciales fueron seleccionados previamente atendiendo a la incidencia que ellos tienen sobre el rendimiento de la RNA. Cada uno de los vectores formados será un estado inicial a partir del cual se comenzarán a generar los siguientes nodos según la heurística planteada.
Forma de tratamiento de los pesos:
- Frecuencia Absoluta.
- Frecuencia Relativa.
- Coeficiente de Correlación de Pearson.
Estrategia de asignación:
- Todas las pertenencias.
- Máxima pertenencia.
- Pertenencia>
Preprocesamiento de los rasgos:
- Rasgo a fuzzificar mediante la variante Triangle.
- Rasgo a fuzzificar mediante la variante All Gaussian.
- Rasgo a fuzzificar mediante la variante Sigmoidea, Gaussian, Sigmoidea.
- Rasgo a fuzzificar mediante la variante * Triangle.
- Rasgo a fuzzificar mediante la variante Triangle, Trapezoid, Triangle.
- Rasgo a discretizar mediante la variante CAIM.
- Rasgo a discretizar mediante la variante Chi_Square.
- Rasgo a discretizar mediante la variante K-Means.
- Rasgo a discretizar mediante la variante Equal_Width.
- Rasgo a discretizar mediante la variante Equal_Frequency.
Para lograr una mayor velocidad en la búsqueda de los vectores de configuración de las redes neuronales se debe utilizar la programación distribuida, que brinda la posibilidad de manejar los recursos de toda una red.
Programación distribuida
La construcción de sistemas distribuidos brinda la posibilidad de utilizar los recursos de toda una red. Los dos tipos principales de sistemas distribuidos son los sistemas computacionales distribuidos y los sistemas de procesamiento paralelo. En programación distribuida, un conjunto de ordenadores conectados por una red son usados colectivamente para realizar tareas distribuidas. Por otro lado en los sistemas paralelos, la solución a un problema importante es dividida en pequeñas tareas que son repartidas y ejecutadas para conseguir un alto rendimiento. Los sistemas distribuidos se pueden implementar usando dos modelos: el modelo cliente – servidor y el modelo basado en objetos. El modelo de cliente-servidor contiene un conjunto de procesos clientes y un conjunto de procesos servidor. Cliente y Servidor deben hablar el mismo lenguaje para conseguir una comunicación efectiva. En el modelo Orientado a Objetos hay una serie de objetos que solicitan servicios (clientes) a los proveedores de los servicios (servidores) a través de una interfaz de encapsulación definida. Un cliente envía un mensaje a un objeto (servidor) y éste decide qué ejecutar. RMI y CORBA son algunos de esos sistemas basados en objetos (Labrador, 2006).
Microsoft .NET Remoting provee un marco que permite que una aplicación pueda comunicarse con otra, tanto si ambas residen en el mismo equipo como si residen en equipos distintos de la misma red de área local o en redes distintas separadas por una gran distancia, incluso si los sistemas operativos que se ejecutan en dichos equipos son diferentes; con la peculiaridad de necesitar ejecutarse sobre Microsoft .Net Framework, del cual existen versiones para Linux y sus homólogos así como para todas las versiones de Windows. Microsoft .NET Framework es un artefacto importante dentro de la arquitectura .Net (Labrador, 2006).
La interfaz de programación de .NET Remoting en la plataforma .NET, tiene otra filosofía respecto a las comunicaciones y formatos de mensajes de otras APIs, como son COM distribuido (DCOM) o la invocación remota de métodos (RMI). En lugar de basarse en un protocolo y en mensajes propietarios, .NET Remoting utiliza estándares muy bien establecidos como SOAP para mensajería y HTTP y TCP como protocolo de comunicación. Incluso se pueden utilizar canales propios o de terceras partes.
Microsoft .NET Remoting oculta todos los detalles de implementación del trabajo con Sockets, entregando al programador final una interfaz de programación que se distingue por las facilidades de uso y su potente alcance. En el siguiente esquema se ejemplifican claramente las diferentes partes que conforman una típica llamada a un objeto remoto en .NET, ver Figura 1 .
RESULTADOS Y DISCUSIÓN
En la tabla se muestra cómo debe quedar el vector de configuración de acuerdo a los modelos de red que se utilizan: el tratamiento a los pesos, la estrategia de asignación y el preprocesamiento de los datos.
La figura 2 muestra cómo se conformarían los vectores de configuración en función del rendimiento de la RNAAs, utilizando el método de búsqueda de algoritmo genético (AG), para un solo atributo.
La búsqueda del vector de configuración se detendrá cuando el rendimiento de la RNAAs, sea mayor que el propuesto como umbral. En la figura 3 se muestra cómo se realizará la búsqueda de la configuración del vector de configuración utilizando la los sistemas distribuidos.
Costo computacional
El costo computacional de la búsqueda del vector de configuración, está relacionado con el tipo de búsqueda que se emplee, es ahí donde debe ser analizado este costo computacional, en el caso de la búsqueda exhaustiva es de O (n!) ya que depende de la exploración de todas las componentes del vector completo, en el caso de la Ascensión de colinas es de O(n), como depende de la información del vector anterior, no tiene que explorar todo el espacio, sino encontrar una solución mejor. El costo computacional del algoritmo PSO es de O(n2), el del algoritmo VMO es O(n3) y para el AG es de O(n4), teniendo en cuenta que O(n) O(n2) O(n3) O(n4) O (n!).
CONCLUSIONES
Con este diseño propuesto se pretende reducir considerablemente el número de configuraciones del vector a explorar, teniendo en cuenta que al determinar que un elemento de este no ofrece una mejora en el desempeño de la RNA, el mismo no volverá a ser examinado al combinarlo con otro de los elementos no explorados y se puede obtener un mayor rendimiento de la RNA, en un determinado tiempo y se evita la búsqueda engorrosa de estos vectores.
REFERENCIAS BIBLIOGRÁFICAS
BELLO , R. E. Aplicaciones de la Inteligencia Artificial. Universidad de Guadalajara. 2002.
BELLO, R. E. P. A. Optimización basada en mallas dinámicas. Su aplicación al problema de selección de rasgos. 2007.
ENGELBRECHT, A. P. Fundamentals of Computational Swarm Intelligence, 2006. John Wiley & Sons.
C. BLUM AND A. ROLI. “Metaheuristics in Combinatorial Optimization: Overview and conceptual Comparison”,TR/IRIDIA. 2001.
FALCÓN, R. J. Herramienta para el desarrollo de sistemas conexionistas en presencia de rasgos difusos., UCLV Marta Abreu. 2003.
FALCÓN, R. J. Plataforma evaluadora de modelos neuroborrosos asociativos., UCLV Marta Abreu. 2006.
FALCÓN, R. J. LABRADOR, A., NAVARRO, A., RODRÍGUEZ, Y. GARCÍA, M. Módulo de Experimentación Combinatoria para la Evaluación de Modelos Neuro-Borrosos Asociativos. UCLV Marta Abreu. 2006.
GOLDBERG, D. E. (Ed.) Genetic Algorithms in Search. Optimization and Machine Learning. 1998. Addison-Wesley Publishing Company: University of Alabama.
GLOVER, F. Tabu search for nonlinear and parametric optimization (with links to genetic algorithms). Discrete Applied Mathematics 49(1-3), 231-255 doi: 10.1016/0166-218X(94)90211-9. 1994.
HOPFIELD, J. J. Neural networks and physical systems with emergent collective computational abilities, Proc. Nat. Acad. Sci. USA. vol. 79: p. 2554-2558. 1982.
HUSSAIN, F. L., H. Discretization: An Enabling Technique. 1999.
JYH-SHING, R. Neuro-Fuzzy and Soft Computing. Prentice Hall. 1998.
KURGAN, L. CAIM Discretization Algorithm. IEEE Transactions on Knowledge and Data Engineering. , Vol 16. No. 2. 2004.
KENNEDY, J. EBERHART, R.C. 1995. Particle swarm optimization. Proc. of On Neural Networks, Piscataway, NJ, pp. 1942-1948.
LABRADOR, A. N. A. M. Módulo de Experimentación Combinatoria para la Evaluación de Modelos Neuro-Borrosos Asociativos. UCLV Marta Abreu. 2006.
LIU, H. A. S. R. CHI2: Attribute selection and discretization of numeric attributes. In Proceedings of the IEEE 7th Conference on tools with AI. 1997.
MCCLELLAND, J. L. y. R. "Explorations in parallel distributed processing.MIT Press". 1989.
MARTÍNEZ- LÓPEZ. Y, “Shell para la construcción de Sistemas Expertos Conexionistas”. , UCLV Marta Abreu. 2010.MOSCATO, P., COTTA. “An introduction to memetic algorithms” Revista Iberoamericana de Inteligencia artificial Nº19. 2003.
NAUCK, D. Foundations of neuro fuzzy systems, John Wiley & Sons, Inc. 1997.
ÖSTERMARK, R. A hybrid genetic fuzzy neural network algorithm designed for classification. 2000.
PURIS A., BELLO, R., MOLINA, D,HERRERA, F. “Variable mesh optimization for continuous optimization problems”, Soft Computing, vol. 16, no. 3, p. 511–525. 2011.
R. YANG. “Line-breeding Schemes for Combinatorial Optimization”, Lectures Notes in Computer Science 1498. Springer-Verlag Berlin. p. 448–457. 1998.
ZADEH, L. A. The fuzzy systems handbook: a practitioner’s guide to building, using and maintaining fuzzy system. 1994.
Recibido: 08/03/2013
Aceptado: 28/10/2013














