Mi SciELO
Servicios Personalizados
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Revista Cubana de Ciencias Informáticas
versión On-line ISSN 2227-1899
Rev cuba cienc informat vol.8 no.4 La Habana oct.-dic. 2014
ARTÍCULO ORIGINAL
Compensatory fuzzy logic for intelligent social network analysis
Lógica difusa compensatoria para el análisis inteligente de redes sociales
Maikel Y. Leyva-Vázquez1*, Rafael Bello-Lara1, Rafael Alejandro Espín-Andrade2
1 Centro de Consultoría y Desarrollo de Arquitecturas Empresariales. Departamento de Soluciones SOA. Universidad de las Ciencias Informáticas, Carretera a San Antonio de los Baños, km 2 ½, Torrens, Boyeros, La Habana, Cuba. CP.: 19370.
2 Universidad de Occidente, Mazatlán, México.
*Autor para la correspondencia:mleyvaz@uci.cu
ABSTRACT
Fuzzy graph theory has gained in visibility for social network analysis. In this work fuzzy logic and their role in modeling social relational networks is discussed. We present a proposal for extending the fuzzy logic framework to intelligent social network analysis using the good properties of robustness and interpretability of compensatory fuzzy logic. We apply this approach to the concept path importance taking into account the length and strength of the connection. Results obtained with our model are more consistent with the way human make decisions. Additionally a case study to illustrate the applicability of the proposal on a coauthorship network is developed. Our main outcome is a new model for social network analysis based on compensatory fuzzy logic that gives more robust results and allows compensation. Moreover this approach makes emphasis in using language for social network analysis.
Keywords: coauthorship network, compensatory fuzzy logic, fuzzy graph, social network analysis.
RESUMEN
La teoría de los grafos difusos ha ganado en visibilidad para el análisis de redes sociales. En este trabajo se discute el rol de las relaciones difusas y su papel en el modelado de redes sociales. En el artículo se presenta una propuesta para extender el marco de trabajo de la lógica difusa al análisis inteligente de las redes sociales usando las propiedades de robustez e interpretabilidad asociadas a la lógica difusa compensatoria. Mediante este enfoque es analizada la importancia de los caminos teniendo en cuenta la longitud y la fortaleza de la conexión entre nodos de la red. Los resultados obtenidos resultan más consistentes con la forma de tomar decisiones en los humanos. Adicionalmente se presenta un estudio de caso basado en el análisis de una red de coautoría mostrando la aplicabilidad de la propuesta. El principal resultado obtenido radica en un nuevo modelo para el análisis de redes sociales basado en la lógica difusa compensatoria brindando resultados más robustos y permitiendo la compensación. Adicionalmente el modelo contribuye al uso del lenguaje en el proceso de análisis de redes sociales.
Palabras clave: análisis de redes sociales, grafos difusos, lógica difusa compensatoria, redes de coautoría.
INTRODUCTION
Recently the ideas of a fuzzy relationship and fuzzy graph have gained in visibility. Fuzzy cognitive maps (Leyva et al., 2014) and the paradigm for intelligent social network analysis (PISNA) (Yager, 2008; Yager, 2014) are two examples. Social networks have become an important technology with examples like Facebook and LinkedIn or ResearcheGate, a network dedicated to researchers.
However the current approaches for social network analysis (SNA) based on fuzzy graphs have some limitations, especially for dealing with sensitivity to changes in the values of truth and compensation when calculating the accuracy of compound predicates (Ortega et al., 2013). Rickard and Yager (2013) propose a method for improving interpretability in SNA using interval type-2 (IT2) fuzzy sets (John and Coupland, 2006). The main drawback with this approach is the high computational cost and the need of preprocessing the information. Another proposal (Brunelli et al., 2014) is based on the construction of higher dimensional fuzzy m-ary adjacency relations from the binary relations by means of ordered weighted averaging (OWA) functions (Yager, 1988). This approach introduces a flexible consensus measure but is not directly applicable to general tasks of social network analysis.
In this paper we propose a model for SNA combining fuzzy graph and compensatory fuzzy logic (CFL) (Andrade et al., 2014a). This combination allows overcoming the limitation in traditional fuzzy logic for SNA to estimate the truth or falsity of observations about a network.
The outline of this paper is as follows: Section 1 is dedicated to fuzzy graphs and Section 2 to compensatory fuzzy logic. The intelligent fuzzy social network analysis based on CFL proposal is presented in Section 3. A case study is discussed in Section 4. The paper closes with concluding remarks, and discussion of future work in Section 5.
COMPUTACIONAL METHODOLOGY
Fuzzy Graph
While crisp relations are appropriate for describing relations like parent of, fuzzy set are better at capturing relationships of degree like friendship (Wierman, 2010). A fuzzy relationship on X is a mapping ![]() where R(x, y) indicates the degree of relationship between x and y (Yager, 2010). This allows extending the connections in a network from connected or not to fuzzy connections. Here we denote a fuzzy graph as
where R(x, y) indicates the degree of relationship between x and y (Yager, 2010). This allows extending the connections in a network from connected or not to fuzzy connections. Here we denote a fuzzy graph as ![]() here V is set of vertices, E is the set of edges and R is a relation
here V is set of vertices, E is the set of edges and R is a relation ![]() .
.
Fuzzy set theory has been applied to social network analysis (SNA) modeling fuzzy relations that exist between entities as graph (Nair and Sarasamma, 2007). A social network can easily be represented by a fuzzy relation or a fuzzy graph extending the analyst´s capabilities of examining networks (Yager, 2008).
Using fuzzy sets it is possible to formalize the idea of vocabulary. For any element![]() , its membership grade,
, its membership grade, ![]() indicate the compatibility of the value y with the linguistic concept W (Yager, 2008). For studying fuzzy graphs, there are a number of attributes about which it will be useful to have vocabularies. Strength of connection and the number of links in a path (link-length) are two of them.
indicate the compatibility of the value y with the linguistic concept W (Yager, 2008). For studying fuzzy graphs, there are a number of attributes about which it will be useful to have vocabularies. Strength of connection and the number of links in a path (link-length) are two of them.
It is possible to define a fuzzy adjacency matrix to represent a social network starting from real world information. If a value adjacency matrix ![]() exist with
exist with ![]() , and v* playing the role of the upper bound, we can rescale each vij into rij with a function
, and v* playing the role of the upper bound, we can rescale each vij into rij with a function ![]() ,
, ![]() (Brunelli and Fedrizzi, 2009).
(Brunelli and Fedrizzi, 2009).
Compensatory Fuzzy Logic
Fuzzy logic is a multivalent logic system introduced by Zadeh (1965) in 1965 at the University of Berkeley (California). Although the many advantages of fuzzy logic to model ambiguous or vague knowledge it have certain drawbacks. The mains limitations in the modeling of knowledge can be summarized as (Alonso et al., 2014):
- The associative property of conjunction and disjunction operators.
- The lack of sensitivity to changes in the values of truth of the basic predicates when calculating the truth value of compound predicates.
- The lack of compensation for the truth values of basic predicates when calculating the accuracy of compound predicates.
CFL is s a variant of fuzzy logic that overcomes the preceding limitations. A CFL system is a quartet of operators: a conjunction, a disjunction, a negation and a strict fuzzy order that satisfies the axioms of compensation, commutativity, strict growth, veto, fuzzy reciprocity, fuzzy transitivity and the Morgan’s laws (Andrade, Fernández and González, 2014a; Andrade et al., 2014c). In this work Geometric Mean Based Compensatory Logic (GBCFL) is used due to the robustness and relative simplicity of its operators (Ortega, Andrade and Gómez, 2013). In GBCFL conjunction is defined as follows:
![]()
The disjunction is defined as the dual of the conjunction:
![]()
The fuzzy negation is:
![]()
and the fuzzy strict order is:
![]()
At any fuzzy predicate P over the universe U, universal and existential propositions are defined respectively as (Andrade et al., 2014b):

The min-max approach of the Zadeh family of operator (Wierman, 2010) used in the PISMA approach is not sensible to the changes in the truth values of predicates. With CFL we can express an “appealing” sensibility and attaint more reliable operators according to the way that human take decisions. Combining the modeling capability of fuzzy graphs and CFL we can provide more realistic formulation of some concepts available in SNA as well as some new concepts.
Intelligent social network analysis based on CFL
The centrality measures have been used for the analysis in fuzzy graphs ( e.g. (Samarasinghea and Strickert, 2011), (Yager, 2010)). The most used centrality measures to identifying a central node are: degree centrality, betweenness centrality, closeness centrality (Samarasinghea and Strickert, 2011). Another way of measuring the centrality of a vertex by the number of other vertices to which it directly connected by at most k steps (Yager, 2008):
![]()
where RK(Vi,Vj) is the strength of the strongest path from Vi to Vj containing at most k links.
Strength (ST) of the path is usually defined as:
![]()
One of the drawbacks of the Min operator is that it leads to a degradation of outcomes by compressing strength, for example on a given node, a very strong relation and a moderate one would have the same partial effect if the previous path strength of influence is weak (Montibeller and Belton, 2009).
In this paper instead we define degree of connection of a path (how strong is a path) taking into account the strength in all its edges:
![]()
where ![]() is the universal proposition in CFL.
is the universal proposition in CFL.
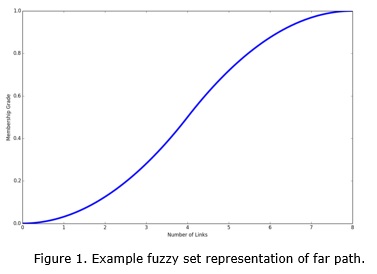
Moreover the length of a path L(p) can be defined as the number of edges the path contains. The word Far (F) can be defined a fuzzy subset ![]() such that F(K) is the degree to which a path of k links is Far. (figure 1).
such that F(K) is the degree to which a path of k links is Far. (figure 1).
We propose to find the better path between two vertices in terms of the negation of its farness and the degree of connection:
![]()
Where ![]() and
and ![]() are the negation and conjunctive operator in CFL respectively.
are the negation and conjunctive operator in CFL respectively.
RESULTS AND DISCUSSION
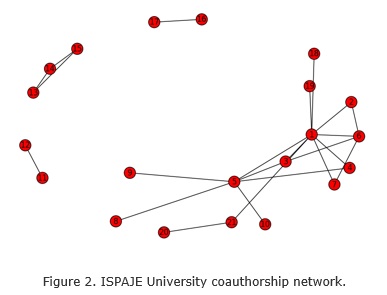
Coauthorship networks (Newman, 2004) are collaboration graph where nodes are scientific. Here we consider that two scientists are connected if they have appeared as authors in the same paper. figure 2 shows the network formed by of research staff at the ISPJAE University inside the Eureka network.
Eureka network is a multinational scientific network. Its objective is the contribution to increase capabilities of useful knowledge discovering for the management of organizations in Iberian American region. For constructing coauthorship network three books published by Eureka have been taking into account (Andrade et al., 2013; Espín et al., 2011; Leyva et al., 2013) .
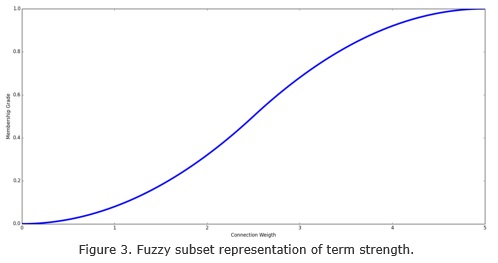
In this case study we analyze the principal component of this network. The strength of connection among adjacency vertices is obtained using the sigmoid membership function with parameters a and b (fig 3):
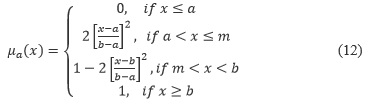
where ![]()
In this case a = 0 and b = 5 = v* (fig 3).
F(K) is calculate with the sigmoid function (12) with parameter a=0, b=8 and m=4 (fig 1).
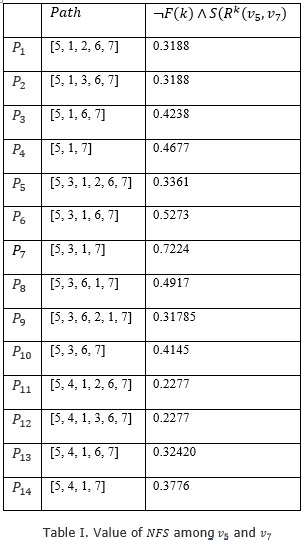
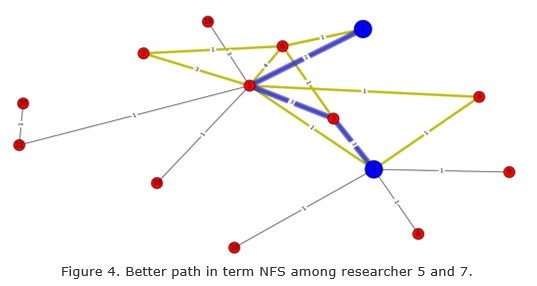
The NFS values of paths among vertices 5 y 7 in shown in table I.
If a ranking were required, this is as follows:
![]()
The better path in term of length and strength among researcher 5 and 7 (NFS(v5,v) = 0.7224) is shown in conjunction with all paths among them in figure 4. The path found is neither shortest (P4) nor strongest (P6), different to results with the min-max approach of Zadeh operators (Wierman 2010) and more consistent with the way that human make decisions.
Comparing our proposal with the PISNA approach as proposed by Yager (2008), we notice that the former model will only gives the most suitable or the shortest path not allowing to express compensation. Additionally our proposal will give more robust results because among fuzzy operators the those belonging to CFL are the most robust (Ortega, Andrade and Gómez, 2013). This results make our model appealing for combining decision making models and social networks analysis specially in recommendation tasks (Al Falahi, et al., 2012) and consensus reaching (Brunelli and Fedrizzi, 2014). Our approach is an opportunity to use the language as key element of communication in the construction of semantic models in SNA (Yager, 2008). It is closer to the objective to make reasoning processes in environments of uncertainty and imprecision with words (Zadeh, 1999).
CONCLUSIONS
In this work we discussed the idea of fuzzy graph and their role in modeling social relational networks. Compensatory fuzzy logic was introduced and we discussed how these technologies can provide the analyst further flexibility for social network analysis. We applied this approach to the concept path importance taking into account the length and strength of the connection.
The new model for intelligent social network analysis based on CFL gives more robust outcomes and allow expressing compensation. The sensibility of the operators in our proposal gives more consistent results with the way that human make decisions. Moreover it bring closer the opportunity to use the language as crucial component in the construction of semantic models in SNA.
As future research we intend to develop models for combining decision making and social networks analysis. Discovering knowledge with linguistic summarization of social networks based on CFL is a promising area. The mining of social relation networks, the development of more flexible ways for querying social networks, and the development of a software tool are other areas of future work.
ACKNOWLEDGEMENT
The authors are grateful to the anonymous reviewers for their valuable suggestions.
Author Maikel Leyva wants to thank to Dra. Macarena Espinilla from Jaén University and to MSc. Yasel Couce for their help.
REFERENCES
AL FALAHI, K., N. MAVRIDIS AND Y. ATIF. Social Networks and Recommender Systems: A World of Current and Future Synergies. In Computational Social Networks. Springer, 2012, p. 445-465.
ALONSO, M. M., R. A. E. ANDRADE, V. L. BATISTA AND A. R. SUÁREZ. Discovering Knowledge by Fuzzy Predicates in Compensatory Fuzzy Logic Using Metaheuristic Algorithms. In Soft Computing for Business Intelligence. Springer, 2014, p. 161-174.
ANDRADE, R. A. E., E. FERNÁNDEZ AND E. GONZÁLEZ. Compensatory Fuzzy Logic: A Frame for Reasoning and Modeling Preference Knowledge in Intelligent Systems In Soft Computing for Business Intelligence. Springer, 2014a.
ANDRADE, R. A. E., E. FERNÁNDEZ AND E. GONZÁLEZ. Compensatory Fuzzy Logic: A Frame for Reasoning and Modeling Preference Knowledge in Intelligent Systems. In Soft Computing for Business Intelligence. Springer, 2014b, p. 3-23.
ANDRADE, R. A. E., E. GONZÁLEZ, E. FERNÁNDEZ AND M. M. ALONSO. Compensatory Fuzzy Logic Inference. In Soft Computing for Business Intelligence. Springer, 2014c, p. 25-43.
ANDRADE, R. A. E., R. B. PÉREZ, A. C. ORTEGA, J. M. GÓMEZ, et al., Soft Computing for Business Intelligence. In.: Springer Berlin Heidelberg, 2013.
BRUNELLI, M. AND M. FEDRIZZI. A fuzzy approach to social network analysis. In Social Network Analysis and Mining, 2009. ASONAM'09. International Conference on Advances in. IEEE, 2009, p. 225-230.
BRUNELLI, M., M. FEDRIZZI AND M. FEDRIZZI Fuzzy m-ary adjacency relations in social network analysis: Optimization and consensus evaluation. Information Fusion, 2014, 17, 36-45.
ESPÍN ANDRADE, R., MARX GÓMEZ J. AND R. V. A. Towards a transdisciplinary technology for Business Intelligence: Gathering Knowledge Discovery, Knowledge Management and Decision Making. In Schriftenreihe der Oldenburger Wirtschaftsinformatik. Aachen, 2011.
JOHN, R. AND S. COUPLAND Extensions to type-1 fuzzy logic: Type-2 fuzzy logic and uncertainty. Computational Intelligence: Principles and Practice, 2006, 89-101.
LEYVA-VAZQUEZ, M., K. PEREZ-TERUEL AND R. I. JOHN. A model for enterprise architecture scenario analysis based on fuzzy cognitive maps and OWA operators. In Electronics, Communications and Computers (CONIELECOMP), 2014 International Conference on. IEEE, 2014, p. 243-247.
LEYVA LÓPEZ J. C., E. A. R., B. P. R. AND Á. C. P. Studies on Knowledge Discovery, Knowledge Management and Decision Support. In.: Atlantis Press, 2013.
MONTIBELLER, G. AND V. BELTON. Qualitative operators for reasoning maps: Evaluating multi-criteria options with networks of reasons. In.: Elsevier, 2009, vol. 195, p. 829-840.
NAIR, P. S. AND S. T. SARASAMMA. Data mining through fuzzy social network analysis. In Fuzzy Information Processing Society, 2007. NAFIPS'07. Annual Meeting of the North American. IEEE, 2007, p. 251-255.
NEWMAN, M. E. Coauthorship networks and patterns of scientific collaboration. Proceedings of the National Academy of Sciences, 2004, 101(suppl 1), 5200-5205.
ORTEGA, M., P. MICHEL, R. E. ANDRADE AND J. MARX GÓMEZ. Multivalued Fuzzy Logics: A Sensitive Analysis. In Fourth International Workshop on Knowledge Discovery, Knowledge Management and Decision Support. Atlantis Press, 2013.
RICKARD, J. T. AND R. R. YAGER. Perceptual computing in social networks. In IFSA World Congress and NAFIPS Annual Meeting (IFSA/NAFIPS), 2013 Joint. IEEE, 2013, p. 691-696.
SAMARASINGHEA, S. AND G. STRICKERT 2011. A New Method for Identifying the Central Nodes in Fuzzy Cognitive Maps using Consensus Centrality Measure. In Proceedings of the 19th International Congress on Modelling and Simulation, Perth, Australia, 12–16 December 2011 2011.
WIERMAN, M. J. An Introduction to the Mathematics of Uncertainty. Edtion ed. Omaha, Nebraska: Center for Mathematics of Uncertainty, Inc., 2010.
YAGER, R. R. On ordered weighted averaging aggregation operators in multicriteria decisionmaking. Systems, Man and Cybernetics, IEEE Transactions on, 1988, 18(1), 183-190.
YAGER, R. R. Intelligent social network analysis using granular computing. International Journal of Intelligent Systems, 2008, 23(11), 1197-1219.
YAGER, R. R. Concept representation and database structures in fuzzy social relational networks. Systems, Man and Cybernetics, Part A: Systems and Humans, IEEE Transactions on, 2010, 40(2), 413-419.
YAGER, R. R. Social Network Database Querying Based on Computing with Words. In Flexible Approaches in Data, Information and Knowledge Management. Springer, 2014, p. 241-257.
ZADEH, L. A. Fuzzy sets. Information and Control, 1965, 8(3), 338-353.
ZADEH, L. A. From Computing with Numbers to Computing with Words—From Manipulation of Measurements to Manipulation of Perceptions. IEEE TRANSACTIONS ON CIRCUITS AND SYSTEMS—I: FUNDAMENTAL THEORY AND APPLICATIONS, 1999, 45(1), 105.
Recibido: 14/05/2014
Aceptado: 15/10/2014