ARTÍCULO ORIGINAL

 

Un modelo de optimización difuso para el problema de atraque de barcos

 

A fuzzy optimization model for the berth allocation problem

 

 

Flabio Gutierrez S.^1*,Mario Rodríguez M.², Federico Barber S.², Edmundo Vergara M.³

¹Universidad Nacional de Piura. Urb. Miraflores s/n, Castilla, Piura, Perú.     [e-mail]
²Universidad Politécnica de Valencia. Camino de Vera, s/n, 46022 Valencia, España. {mrodriguez,fbarber}@dsic.upv.es [e-mail], [e-mail]
³Universidad Nacional de Trujillo. Calle Diego de Almagro 344, Trujillo, Perú. [e-mail]

*Autor para la correspondencia: [e-mail]

 

 

---

RESUMEN

El problema de asignación de atraques (BAP) en un terminal marítimo de contenedores se define como la asignación factible de atraques a los barcos entrantes. En este trabajo, desarrollamos un modelo de optimización difusa para el BAP continuo y dinámico. Se asume que el tiempo de llegada de los barcos es impreciso, en el sentido que los barcos pueden adelantarse o retrasarse hasta una tolerancia permitida. Se utilizan conjuntos difusos para representar la imprecisión en la llegada de los barcos. Para la solución del modelo se aplica el método de α – cortes. El modelo propuesto ha sido codificado en CPLEX y evaluado en diferentes instancias. Los resultados obtenidos muestran que el modelo propuesto puede ayudar a los administradores de un terminal marítimo de contenedores, pues tiene a su disposición planes de atraque con diferente grado de adelanto o retraso permitido y optimizados respecto al tiempo de espera.

Palabras clave: alpha – cortes, conjuntos difusos, imprecisión, optimización difusa, problema de asignación de atraque

---

ABSTRACT

The berth allocation problem (BAP) in a maritime container terminal is defined as a feasible allocation of berths to incoming vessels. In this paper, we developed a fuzzy mathematical programming model for continuous and dynamic BAP. It is assumed that the arriving time of vessels is imprecise, in the sense that the vessels can have an advance or delay but only up to a permitted tolerance.  Fuzzy sets are used to represent the imprecision. α – cuts method is applied to the model solution.  The proposed model has been codified in CPLEX solver and evaluated in different instances. The obtained results show that the proposed model can help the container terminal managers, since it has available berth plans with different degrees of allowed advance or delay, which are optimized according to the waiting time.

Key words: alpha – cuts, fuzzy sets, imprecision, fuzzy optimizaticon, berth allocation problema.

---

 

 

INTRODUCCIÓN

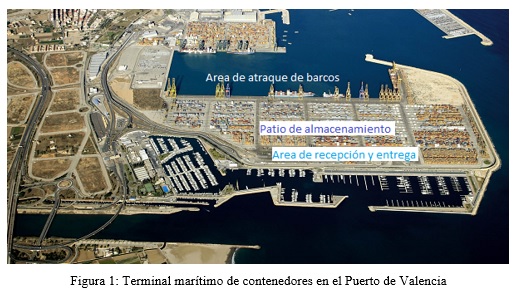
Aproximadamente el 80% del mercado global se lleva a cabo a través del mar (Buhrkal y otros, 2011), y mayormente se transfieren en contenedores. Los contenedores son cajas grandes de metal hechas en medidas estándar y se miden en múltiplos de 20 pies llamado “twenty-foot equivalent units” (TEU).  El volumen del comercio en contenedores en el 2012, llegó a 155 millones de TEUs. (U. N. Publications, 2013). Los terminales portuarios que manejan contenedores son llamados terminales marítimos de contenedores (TMC), estos tienen diferentes y más complejas operaciones que los puertos de pasajeros o los puertos de carga y descarga a granel.  Un TMC, generalmente sirve como zona de transbordo entre barcos y vehículos terrestres (trenes o camiones). Los TMC, son sistemas abiertos con tres áreas diferenciadas (ver Figura 1): el área de atraque, donde los barcos son atracados para el servicio (cargar o descargar contenedores); el patio de almacenamiento de contenedores, donde los contenedores se almacenan temporalmente mientras esperan a ser exportados o importados; y el área de recepción y entrega, que conecta el terminal de contenedores con el sistema de transporte al interior de un país (abastecimiento para la exportación o distribución en caso de importación). Cada uno de ellos presenta diferentes problemas de planificación y scheduling para ser optimizados (Steenken, y otros, 2004), por ejemplo, la asignación de muelle, planificación de la estiba, scheduling de las grúas del muelle deben ser gestionados en el área de atraque; el problema de apilamiento de contenedores, las operaciones de transporte horizontal deben llevarse a cabo en el patio de contenedores.

En este trabajo se aborda el problema de asignación de atraques, también conocido como BAP (Berth Allocation Problem), un problema NP-duro de optimización combinatoria (Lim, 1998), que consiste en asignar a cada barco entrante una posición de atraque en el muelle. Una vez que el barco llega al puerto, entra en tiempo de espera para atracar en el muelle. Los administradores de los TMC se enfrentan a dos decisiones relacionadas: dónde y cuándo los barcos deben atracar.

Los tiempos reales de la llegada de los barcos son bastante inciertos, esta incertidumbre depende, por ejemplo, de las condiciones meteorológicas (vientos, tormentas), problemas técnicos, otros terminales que el barco tiene que visitar o por otras razones. Los barcos pueden llegar respectivamente antes o después de su tiempo de llegada prevista (Bruggeling, y otros, 2011; Laumanns, y otros, 2010), sólo la mitad de los barcos llega a tiempo (Consultants D, 2008). Esto tiene efectos en las operaciones de carga y descarga, otras actividades del terminal, y, por tanto, en los servicios requeridos por el cliente.

Los administradores de los TMC cambian o revisan los planes, pero una revisión frecuente del plan de atraque no es deseable desde el punto de vista de la planificación de recursos (Dai, 2008). Por lo tanto, la capacidad de adaptación del plan de atraque es importante para la buena performance del sistema que maneja un TMC. Como resultado, el posible adelanto o retraso en la llegada de los barcos, debe considerarse al hacer un plan de atraque.

Hay varios tipos de incertidumbre, como la aleatoriedad, imprecisión (ambigüedad, vaguedad), la confusión. Varios tipos de incertidumbre puede ser categorizados como estocásticos o difusos (Zimmermann, 2001).

Los conjuntos difusos están especialmente concebidos para hacer frente a la imprecisión.

En este trabajo se presenta un modelo difuso para el BAP continuo y dinámico. Se asume que el tiempo de llegada de los barcos es impreciso, en el sentido que los barcos pueden adelantarse o retrasarse en su llegada.

 

MATERIALES Y MÉTODOS

Revisión de literatura

Hay varios atributos para clasificar los modelos relacionados con el BAP (Bierwirth and Meisel, 2010), los más importantes son: el espacial y el temporal.  El atributo espacial puede ser discreto o continuo. Para el caso discreto, el muelle es visto como un conjunto finito de atraques, donde cada atraque se describe por segmentos de longitud fija, usualmente, un atraque solo sirve a un barco a la vez; para el caso continuo, los barcos pueden atracar en posiciones arbitrarias dentro de los límites del muelle. El atributo temporal puede ser estático o dinámico. Para el caso estático, se asume que todos los barcos están en el puerto antes de realizar el plan de atraque; en el caso dinámico, los barcos pueden llegar al puerto en diferentes tiempos, durante el horizonte de planificación.   En (Bierwirth and Meisel, 2010; Stahlbock and Voÿ, 2008), los autores hacen una exhaustiva revisión de la literatura existente sobre el BAP. Hasta donde conocemos, en la literatura hay muy pocos estudios que traten el BAP con datos imprecisos.

Un trabajo que trató con entornos deterministas y difusos para la distribución de contenedores fue presentado en (Seyedhoseini & Damghani, 2009). Los autores desarrollaron un modelo de programación binaria con parámetros difusos. Las distancias entre el muelle y la zona de terminales, el número de contenedores en un barco que ha llegado y la estimación del área disponible en cada terminal en un puerto, fueron asumidos en una condición imprecisa. La imprecisión se representó con números difusos trapezoidales. El objetivo es minimizar la distancia total recorrida por los contenedores desde el barco, hasta a la zona de terminales que les fueron asignados.  El problema de asignación de atraques es tratado como un BAP discreto y estático y no consideran imprecisión en la llegada de los barcos. Un modelo planteado como problema lineal entero mixto (MILP) difuso para el BAP discreto y dinámico fue propuesto en (Melián -Batista, y otros, 2010). Los tiempos de llegada de los barcos están representados por números difusos triangulares. Se presenta el modelo y el diseño de un método de solución basada en MILP paramétrica, aunque no se muestra su evaluación, pero, no tratan el BAP continuo. Según (Bierwirth, 2010), para el diseño de un modelo continuo, la planificación del atraque es más complicada que para un diseño discreto, pero se tiene la ventaja de una mejor utilización del espacio del muelle. En (Gutiérrez, y otros, 2014), se propone un modelo MILP difuso para el BAP continuo y dinámico, el modelo solo contempla posibles retrasos, pero no la posibilidad de adelantarse.

En este trabajo proponemos un modelo de optimización difusa para el BAP continuo y dinámico. Suponemos que los barcos pueden retrasarse o adelantarse un cierto tiempo tolerable o permitido. Esta tolerancia se representa con un conjunto difuso con función de pertenencia de tipo triangular.

Conjuntos Difusos

Los conjuntos difusos ofrecen un entorno flexible para optimizar sistemas complejos. A continuación, se presenta algunos conceptos necesarios en el planteamiento de este trabajo.

Definición 1.  Sea X el universo del discurso, un conjunto difuso en X es un conjunto de pares:

Donde es llamada función de pertenencia, (x) representa el grado en que x pertenece al conjunto .

Para nuestros propósitos, nos restringimos a conjuntos difusos definidos en el conjunto de los números reales Una función de pertenencia puede ser triangular, trapezoidal, sigmoidal, etc.

Definición 2.     El conjunto difuso en es normal si  

Definición 3.   El conjunto difuso en es convexo si y solamente si la función de pertenencia de satisface la inecuación.

Definición 4.     Un número difuso es un conjunto difuso normal y convexo

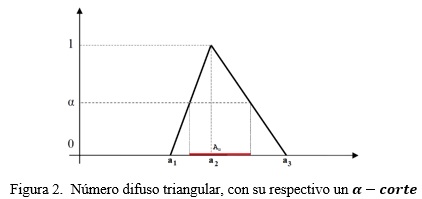
Un número difuso triangular (NDT) (Figura 2) puede ser representado  como = (a₁, a₂ , a₃)

Definición 5.     Sea = (a₁, a₂ , a₃) un número difuso y un número real  Se llama al conjunto clásico

El concepto de permite un enfoque muy interesante de la teoría de conjuntos difusos, ya que la familia formada por los contiene toda la información sobre el conjunto difuso. Mediante el ajuste del valor a se puede determinar el rango o conjunto de valores que satisfacen un determinado grado de pertenencia (presunción, certeza, son otras expresiones utilizadas), o expresado de otra manera el nivel de satisfacción, precisión del resultado o robustez del modelo.

Si consideramos el conjunto difuso con función de pertenencia de tipo triangular, A = (a₁, a₂ , a₃) de la Figura 2, entonces:

Distribuciones de posibilidad

La ambigüedad se puede representar con distribuciones de posibilidad (Zadeh, 1999). Estas distribuciones permiten formalizar de manera muy fidedigna gran cantidad de situaciones en la que se estiman magnitudes localizadas en el futuro. La medida de posibilidad de un evento puede ser interpretado como el grado de posibilidad de su ocurrencia en virtud de la distribución de posibilidad. Entre los diversos tipos de distribuciones, la triangular y la trapezoidal son los más comunes en la solución de problemas de programación matemática posibilista.

Formalmente, las distribuciones de posibilidad son números difusos, nos concentraremos en el NDT = (a₁, a₂ , a₃) el cual está determinado por tres cantidades: a₂ es el valor con más posibilidad de ocurrencia, a₁ y a₃ son los valores límites inferior y superior permitidos, respectivamente ( Figura 2). Por ejemplo, estos valores límite pueden interpretarse como el más pesimista y el más optimista, en función del contexto.

Programación matemática difusa

La programación matemática difusa puede ser de gran ayuda para manejar situaciones en problemas de optimización que incluye parámetros imprecisos (Luhandjul, 2007).  Hay diferentes enfoques para la programación matemática difusa dependiendo del tipo de imprecisión en los parámetros del modelo a optimizar. La programación difusa trata con parámetros vagos (Ramík, 2001), por otra parte, la programación posibilista trata la ambigüedad, es decir, los datos disponibles se conocen exactamente, aunque estos datos pueden variar dentro de un límite de tolerancia. En este caso, los parámetros se consideran como números difusos asociados con distribuciones de posibilidad (Lai and Hwang 1992; Lodwick and Untiedt, 2010).

 

RESULTADOS Y DISCUSIÓN

Modelo BAP difuso con imprecisión en la llegada de los barcos.

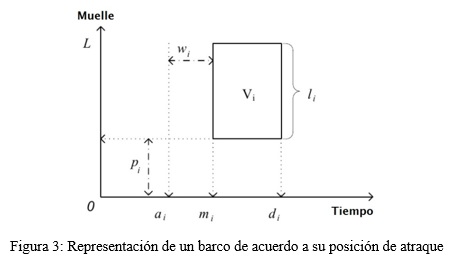
En esta sección, se presenta un modelo difuso para el BAP continuo y dinámico. Se inicia presentando la notación de los principales parámetros que se utilizaron en el modelo (Figura 3):

L: longitud total del muelle del TMC; H: horizonte de planificación.  V: el conjunto de barcos entrantes. Los datos del problema para cada barco i V están dadas por : ai : tiempo de llegada al puerto; wi = mi - ai, tiempo de espera del barco desde que llega hasta que atraca; li : longitud del barco; hi : tiempo de estancia del barco en el lugar de atraque (tiempo de servicio). Con estos datos, se deben decidir las variables: mi : Tiempo de atraque del barco;   pi : Posición donde será atracado el barco. El tiempo de partida del barco di dependerá de mi y hi. La posición de atraque pi se determinará de acuerdo a la longitud de barco. Además, se tiene en cuenta las siguientes suposiciones: Toda la información relativa a los barcos en espera se conoce de antemano, cada barco tiene un calado menor o igual que el muelle, el momento de atraque y desatraque no consume tiempo, está permitido el atraque simultáneo, no se considera distancia de seguridad entre los barcos. El objetivo es distribuir los barcos, minimizando el tiempo total de espera cumpliendo ciertas restricciones: el tiempo de atraque debe ser al menos el mismo que el tiempo de llegada: mi ≥ ai, hay suficiente espacio contiguo en el muelle para atracar la embarcación: pi + li ≤ L.

Se asume que el tiempo de llegada de un barco es ambigua (imprecisa), en el sentido que los barcos pueden adelantarse o retrasarse hasta una cierta tolerancia permitida.

La llegada de cada barco se representa con una distribución de posibilidad triangular como en la Figura 2, es decir, se considera que la llegada no será antes de a₁ , ni después de a₂, la llegada con la máxima posibilidad es a₃.

En la Figura 4, se muestra las distribuciones de posibilidad triangulares para la llegada de tres barcos. Por ejemplo, para el barco 1, la llegada no será antes de la 1 am., ni después de las 4 a.m. la llegada con la máxima posibilidad es a las 2 a.m.

Formalmente, consideramos que la imprecisión en la llegada de los barcos es un NDT = (a₁, a₂ , a₃)

Con la posibilidad de adelanto o retraso en las llegadas y en base al modelo determinista (Kim and Moon, 2003), se propuso el siguiente modelo difuso para manejar la imprecisión en el BAP.

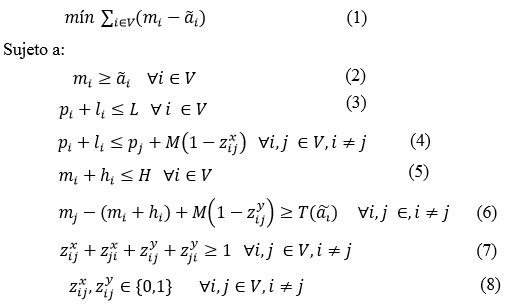
Donde es una variable de decisión que indica si el barco i  está localizado a la izquierda del barco j en el atraque ( = 1), = 1 indica que el tiempo de atraque del barco i  está antes que el del barco j. M es una constante entera grande. La restricción (6), obliga que para un barco j  que atraca después del barco i, su tiempo de atraque m_j  incluya la precisión que se le puede tolerar al barco i.  El modelo (1) -(8) representa a un problema de programación lineal entero mixto difuso, cuyo método de solución se presenta en la siguiente sección.

Solución del modelo BAP difuso

De acuerdo a la sección previa la llegada imprecisa de un barco se representa con el NDT = (a₁, a₂ , a₃). Según la definición 6, su está dado por:   

El corte representa el intervalo de tiempo que se permite o tolera en la llegada de un barco, para un grado de precisión a. El tamaño de ese intervalo  T(a) = (1 - a) (a₃ - a₁ ) , es el tiempo que se tolera en la llegada del barco, el cual debe ser tomado en cuenta en el tiempo de atraque del barco que atracará después.

Se puede observar que para el valor a, el adelanto permitido es: ta(a) = (1 - a) (a₂ - a₁ ), el retraso permitido es:  tr(a) = (1 - a) (a₃ - a₂ ) ,   con lo cual    T(a) = ta(a) + tr(a).

En la Figura 4, se muestra los alfa cortes para la llegada de tres barcos, con un nivel   a = 0.5.

Utilizando los alfa cortes como método de desfuzificación a la llegada difusa de los barcos, una solución al modelo BAP difuso se obtiene del siguiente modelo paramétrico MILP. Figura 5

El horizonte de planificación está dado por

Evaluación

Los experimentos fueron realizados en 50 instancias, que consisten de 8 barcos con una distribución uniforme en los tiempos de llegada imprecisos. Todas las instancias tienen las mismas características de los barcos (tiempo de servicio y longitud), así como el tiempo de llegada con más posibilidad a2. Pero, todas las instancias tienen diferentes valores para el mínimo y máximo tiempo de llegada permitido, a1 y a3 respectivamente.

La longitud del muelle es L=700. El algoritmo ha sido codificado y resuelto en forma óptima en CPLEX. Las instancias fueron resueltas en una computadora personal equipada con un Core (TM) i5 – 4210U CPU 2.4 Ghz con 8.00 Gb RAM.

Los experimentos se llevaron a cabo con un "timeout" (tiempo de cómputo máximo) de 60 minutos.

Para el reporte de los datos, se utilizan los parámetros siguientes: m1i: Tiempo de atraque mínimo permitido, m2i: Tiempo de atraque óptimo, m3i: Tiempo de atraque máximo permitido, tai: Tiempo de adelanto permitido, tri: Tiempo de retraso permitido, d1i: Tiempo de salida mínimo permitido, d2i: Tiempo de salida óptimo, d3i: Tiempo de salida máximo permitido.

 

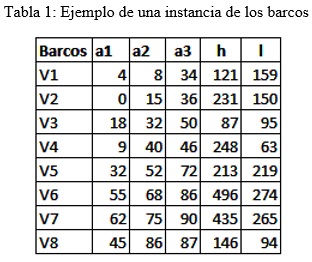
Una instancia se muestra en la Tabla 1, en la Figura 6, se muestra las funciones de pertenencia para la llegada de los barcos de la instancia de la Tabla 1. Por ejemplo, el barco V1 debe llegar a las 8 unidades de tiempo, pero se le permite adelantarse y retrasarse hasta 4 y 34 unidades de tiempo respectivamente.

El valor de a , representa el grado precisión permitido a los barcos. Por ejemplo, a = 1, significa una llegada exacta es decir, no se tolera adelantos y retrasos;  a = 0 , es la máxima ausencia de precisión (imprecisión) permitida.

Para cada una de las instancias y para cada uno de los barcos, considerando once grados de retrasosα = {1;0,9;...;0}, se generaron 11 planes de atraque.

Como un ejemplo ilustrativo, para la instancia de la Tabla 1, tres planes de atraque diferentes se muestran en la Tabla 2, y en forma gráfica en la Figura 7. Estos planes fueron obtenidos con el modelo paramétrico, variando el valor de α = {O; 0,5; 1}.

Para α=1, en todos los barcos los adelantos y retrasos son ta = 0 y tr =0 respectivamente, es decir no se permite adelantos y retrasos en los barcos (parte superior de la Figura 7).  En la mayoría de los casos, si un barco se atrasa en llegar respecto a su tiempo preciso de llegada este plan deja de ser válido.  Por ejemplo, el barco V3 tiene un tiempo de atraque m2=32 y tiempo de salida d2=119, si este barco se atrasa, el barco V8 no puede atracar en su tiempo asignado m2 = 119, y el que le sigue, el barco V7 tampoco puede atracar en su tiempo asignado m2 = 265. Para un número mayor de barcos (como es en la realidad), el retraso de los barcos complica aún más los planes de atraque.

Para un grado de precisión α=0,5, por ejemplo, para el barco V3, el tiempo de atraque óptimo es m2=32, el adelanto permitido es ta= 7, el retraso permitido es tr = 9, es decir, el barco puede atracar en el intervalo de tiempo [25, 41], y puede salir en el intervalo de tiempo [112, 128].  Después del barco V3, el barco V8 puede atracar en el tiempo m2 = 128 con un adelanto permitido de ta =21 y retraso permitido de tr=0,5, el tiempo óptimo de atraque es m2 = 148,5, pero pude atracar en el intervalo de tiempo [128; 149] (Ver Figura 7, parte intermedia).

En α=0 (mínima precisión permitida), los adelantos y retrasos son incrementados, por ejemplo, para el barco V3, el tiempo óptimo de atraque es m2=32 (el mismo que para α = 0:5), pero el adelanto permitido es ta=14 y el retraso permitido es tr=18. Por lo tanto, el intervalo de tiempo donde el barco puede atracar es [18, 50] (Ver Figura 7, parte inferior).

Por la forma como se ha construido el modelo, para cada valor de α, los adelantos y retrasos permitidos son proporcionales a su tiempo máximo adelanto y de retraso. Por ejemplo, para α=0,5, el barco V1 puede adelantarse y retrasarse hasta un máximo de 2 y 13 unidades de tiempo respectivamente. Si α=0, los adelantos y retrasos para el barco V1, son 4 y 26 respectivamente (Ver Tabla 2)

Para las cincuenta instancias, la Figura 8 (a), ilustra la variación del promedio de la función objetivo (FO) con respecto al grado de precisión α. Hay una relación lineal entre el grado de precisión y el promedio de la FO, el decremento del grado de precisión, incrementa el promedio de la FO, por ejemplo, para un grado de precisión α = 0,5, el promedio de la FO es 459,27; y para α = 0 el promedio de la FO es 516,90.

El tomador de decisiones del TMC, puede escoger un plan de acuerdo al par (α; Función Objetivo) que sea una solución satisfactoria. Por ejemplo, si se desea el plan más óptimo, aunque no permita adelantos ni retrasos en la llegada de los barcos, puede escoger el par (1; 401); si se desea un plan con 0,5 de precisión en la llegada de los barcos, aunque se pierda optimalidad, tiene la posibilidad de elegir el par (0,5; 459,27)

Por otro lado, en laFigura 8 (b), se muestra el promedio del Tw y el tiempo de cómputo de las 50 instancias para los diferentes grados de precisión permitidos. El menor Tw = 401 se obtiene con tiempo de 2:59 segundos, correspondiente a un grado de precisión α = 1; y el mayor Tw = 516,90, se obtiene en un tiempo de 2,95 segundos correspondiente a un grado de precisión α = 1.

 

CONCLUSIONES

El sistema de un TMC requiere herramientas que ayuden a los administradores en la toma de decisiones. El BAP es uno de los problemas más críticos y estudiados en los TMC. Muchas investigaciones se han desarrollado sobre el BAP, sin embargo, la mayoría asume que la llegada de los barcos es determinista. Esto no es real, en la práctica pueden ocurrir adelantos o retrasos en las llegadas de los barcos. Por lo tanto, la adaptabilidad de un plan de atraque es importante para el rendimiento global del sistema en un TMC.

En este trabajo, se ha presentado un modelo MILP difuso para el BAP continuo y dinámico. En el modelo propuesto, se asumió que el tiempo de llegada de los barcos es impreciso, en el sentido que los barcos pueden adelantarse o retrasarse hasta un grado de tolerancia permitido. Esta imprecisión se representó mediante conjuntos difusos con función de pertenencia de forma triangular.

Se utilizó el método de para transformarlo en un problema de programación lineal paramétrica.

El modelo propuesto fue codificado y resuelto en forma óptima con la herramienta de optimización CPLEX. El modelo ha sido evaluado por medio de 50 instancias de ocho barcos. Se utilizó ocho barcos con fines ilustrativos, pero el modelo se comporta de la misma manera para un número mayor de barcos.

Los resultados obtenidos mostraron que el procedimiento puede ayudar a los administradores de un TMC en la toma de decisiones, pues tiene a su disposición planes de atraque con diferentes grados de precisión y optimizados respecto al tiempo de espera, con la característica que, a más precisión en la llegada de un barco, el modelo le otorga un tiempo de atraque más preciso.

Finalmente, como resultado de la investigación, se abren posibilidades para futuras investigaciones:

(i)  Extender el modelo propuesto, para tratar con problemas de optimización que contemplen la imprecisión que aparece en las llegadas y el tiempo de servicio de los barcos.

(ii)  Usar metaheuristicas con optimización difusa con el fin de solucionar en forma más eficiente el BAP difuso.

 

AGRADECIMIENTOS

Para la realización de este trabajo se ha contado con ayuda del Fondo para la Innovación Ciencia y Tecnología del Perú FINCyT  (Proyecto    PIBA-2-P-069-14).

 

REFERENCIAS BIBLIOGRÁFICAS

BIERWIRTH, C. & MEISEL, F. A survey of berth allocation and quay crane scheduling problems in container terminals. European Journal of Operational Research, 2010, 202: p.615 627.

BRUGGELING, M.; VERBRAECK, A. & HONIG, H. Decision support for container terminal berth planning: Integration and visualization of terminal information. In Proceedings van de VervoerslogistiekeWerkdagen. University Press, Zelzate, 2011, p. 263 - 283.

BUHRKAL, K.; et al.  Models for the discrete berth allocation problem: A computational comparison. Transportation Research Part E: Logistics and Transportation Review, 2011, 47(4): p. 461-473.

CONSULTANTS D. The drewry container shipper insightthird quarter 2008. Drewry Shipping Consultants: London. 2008, p.83.

DAI, J., LIN, W.; MOORTHY, R. & TEO, C. Berth allocation planning optimization in container terminals. Supply Chain Analysis, 2008, p. 69-104.

GUTIÉRREZ, F; RODRÍGUEZ; M.; BARBER F.; VERGARA E. Un modelo de optimización difuso para asignación de atraques con retrasos en la llegada de los barcos. X SELASI. X Seminario Euro Latinoamericano de Sistemas de Ingeniería. La Habana – Cuba. 2014, p. 758-770.

KIM, K. & MOON. K. Berth scheduling by simulated annealing. TransportationResearchPart B: Methodological, 2003,37(6): p.541-560.

LAI, Y.  & HWANG, C. A new approach to some possibilistic linear programming problems. Fuzzy Sets and Systems, 1992, 49(2): p.121-133.

LAUMANNS, M.; et al. Robust adaptive resource allocation in container terminals. En Proc. 25th Mini-EURO Conf. Uncertainty and Robustness in Planning and Decision Making, Coimbra, Portugal, eds. CH Antunes, DR Insua and LC Dias. 2010. p. 501-517.

LIM. A. The berth planning problem. Operations Research Letters, 1998, 22(2): p.105- 110.

LODWICK, W. & UNTIEDT, E. Introduction to fuzzy and possibilistic optimization. En Fuzzy Optimization. Springer Berlin Heidelberg, 2010. p. 33-62.

LUHANDJUL, M. Fuzzy mathematical programming: Theory, applications and extension. Journal of Uncertain Systems, 2007, 1(2): p.124-136.

MELIÁN-BATISTA, B.; MORENO-VEGA, J.  & GALDEANO, J. Una primera aproximación al problema de asignación de atraques con tiempos de llegada difusos. XV Congreso Español Sobre Tecnologías y Lógica Fuzzy, 2010.

RAMÍK, J. Soft computing: overview and recent developments in fuzzy optimization. Ostravskáuniverzita, Listopad, 2001, p.33-42, 2001.

SEYEDHOSEINI, S.  & DAMGHANI, K. Fuzzy containers allocation problem in maritime terminal. Journal of Industrial Engineering and Management, 2009, 2(2); p. 323-33

STAHLBOCK, R. & VOŸ, S. Operations research at container terminals: a literatura update. Or Spectrum, 2008, 30(1): p.1-52.

STEENKEN, D.; VOŸ, S. & STAHLBOCK, R. Container terminal operation and operations research-a classification and literature review. OR spectrum, 2004, 26(1): p.3-49.

U.N. PUBLICATIONS.  Review of maritime transport. United Nations Conference on Trade and Development (UNTAC), 2013, p. 23- 24.

ZADEH, L. Fuzzy sets as a basis for a theory of possibility. Fuzzy sets and systems, 1999, 100: p.9-34.

ZIMMERMANN, H. Fuzzy set theory and its applications. Fourth, Revised Edition. Springer, 2001.

 

 

Recibido: 17/08/2016
Aceptado: 10/10/2016