My SciELO
Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO
Related links
-
 Similars in
SciELO
Similars in
SciELO
Share
Revista Cubana de Ciencias Informáticas
On-line version ISSN 2227-1899
Rev cuba cienc informat vol.11 no.1 La Habana Jan.-Mar. 2017
ARTÍCULO ORIGINAL
Marcadores para Segmentación Watershed Usando Transformada de Radon
Watershed Segmentation Markers Using Radon Transform
A. González Betancourt1*,P. Rodríguez Ribalta1, R. Orozco-Morales1
1 Centro de Estudios de Electrónica y Tecnologías de la Información, Universidad Central “Marta Abreu” de Las Villas, Cuba, {anier,prodriguez,rorozco}@uclv.cu
*Autor para la correspondencia: anier@uclv.cu
RESUMEN
La determinación de marcadores en imágenes puede ser muy útil tanto en imagenología médica como en fotografía convencional. La imposición automática de marcadores en imágenes médicas es una de las cuestiones propuestas en los últimos años por muchos trabajos, por su gran aplicación en el procesamiento digital, pero no existe un algoritmo global. En este trabajo se presenta la utilización de la transformada Radon para determinar marcadores de eritrocitos en imágenes de microscopia celular de glóbulos rojos con fines de segmentación watershed. Para ello, la búsqueda de marcadores se realiza basada en la propiedad de la transformada Radon de detectar parámetros de forma y su comportamiento ante estructuras circulares. Partiendo de una imagen de microscopía óptica de campo claro con extendido de sangre, se determina una imagen gradiente. A la imagen gradiente se le aplica la transformada Radon directa, para después filtrar cada una de las proyecciones del sinograma con un filtro adaptado. Con la transformada Radon reversa se obtiene una imagen con picos en los eritrocitos. Con un umbral automático se obtiene una imagen marcadora que determina la posición de los eritrocitos. En evaluaciones realizadas con diversas imágenes que contienen un total de 1120 eritrocitos con diferente grado de aglomeración se obtuvo una exactitud del 86.54 %, una sensibilidad del 88.02 %, una predictividad positiva del 97.37 % y una medida-F del 92.39 %, resultados comparables con otros métodos publicados.
Palabras clave: imagen gradiente, marcadores, sinograma, transformada Radon.
ABSTRACT
The determination of markers in images can be very useful both in medical imaging and in conventional photography. The automatic imposition of markers on medical images is one of the issues proposed in recent years by many works, due to their great application in digital processing, but there is no global algorithm. This work presents the use of the Radon transform to determine erythrocyte markers in cellular red cell microscopy images for watershed segmentation purposes. For this, the search of markers is made based on the property of the Radon transform to detect shape parameters and their behavior in relation to circular structures. Starting from a clear field optical microscopy image with blood smear, a gradient image is determined. To the gradient image is applied the direct Radon transform, to then filter each of the projections of the sinogram with an adapted filter. With the Reverse Radon transform, an image with peaks in the erythrocytes is obtained. With an automatic threshold, a marker image is obtained that determines the position of the erythrocytes. An accuracy of 86.54%, a sensitivity of 88.02%, a positive prediction of 97.37% and an F-measure of 92.39% were obtained in evaluations performed with diverse images containing a total of 1120 erythrocytes with different degree of agglomeration, results comparable with other published methods.
Key words: gradient image, markers, radon transform, sinogram.
INTRODUCCIÓN
La malaria es una enfermedad producida por un parásito del género Plasmodium. De acuerdo con el Reporte Mundial de Malaria en 2015 a pesar de los avances a nivel global, 3.200 millones de personas, la mitad de la población mundial, está en riesgo de malaria. En el año 2015, se produjeron 214 millones de casos, con 438.000 muertes (Rocha. D, 2015).
Existen dos técnicas clásicas usadas para el diagnóstico de la enfermedad de la malaria. La que generalmente es usada es el diagnóstico clínico basado en los síntomas tales como fiebre alta, dolor de cabeza, escalofríos severos y molestias en el cuerpo. Sin embargo, estos síntomas no son específicos de malaria, por lo que la fiabilidad del diagnóstico clínico es muy baja. La segunda técnica es el diagnóstico mediante la microscopía óptica de extendidos delgados de sangre periférica, pero la misma requiere un examinador experto para tomar las muestras y analizarlas. Mientras que las muestras sean bien preparadas y examinadas el diagnóstico es muy fiable, permitiendo la determinación del tipo de malaria, el estado de maduración del parásito y el grado de infección (WHO, 1991). Los métodos de reconocimiento manual suelen llevar mucho tiempo y esfuerzo por parte del analista, especialmente en situaciones donde se requiera el análisis de muchas muestras.
Gracias a los avances computacionales se pueden realizar algoritmos que permitan llevar a cabo este engorroso trabajo de forma automática, el cual está libre de fatigas tras el análisis de varias muestras.
El conteo de las células y la detección de parásito por un software computacional es tema de estudio en los últimos años. Por ello es necesaria la búsqueda de métodos rápidos y eficientes que detecten la presencia de estos, previniendo un falso diagnóstico.
Después de obtener las imágenes uno de los primeros pasos para el reconocimiento de patrones, es una buena segmentación de la imagen para poder analizar cada uno de los objetos presentes en la misma. Los métodos propuestos hasta el momento son variables, pero debido a las características de las imágenes es necesaria la implementación de uno que separe todas las células, incluso las aglomeradas. La transformada watershed es una herramienta de procesamiento morfológico que permite segmentar imágenes (Maragos.P, 1996), (Soille.P, 2004). Esta transformada se adapta a los diferentes tipos de imágenes siendo capaz de distinguir objetos sumamente complejos que no pueden ser procesados correctamente mediante algoritmos convencionales. El éxito de la transformada watershed depende fundamentalmente de la existencia de marcadores unívocos para cada uno de los objetos de interés. En el caso que nos ocupa, cada uno de los eritrocitos de la imagen.
La búsqueda de marcadores ha sido propuesta por diferentes vías. En 2015 Benson. C. C. y colaboradores (Benson. C, 2015) publican la búsqueda de marcadores para imágenes médicas de rayos X, CT, MRI, ultrasonido, PET, SPECT y fMRI. Para estas imágenes obtiene una exactitud, aplicando métodos basados en clustering del 85.0 %, aplicando métodos de umbralado del 77.5 % y aplicando métodos basados en morfología del 93.75%. La morfología matemática ha sido empleada en ello por ser un método automático, de fácil implementación y bajo costo computacional (Valdés.L, 2010), no obstante, para el caso de eritrocitos aglomerados, esta falla debido a que cuando el grado de solapamiento es elevado, o se aglomeran varios eritrocitos, usualmente se produce una sola marca.
También existen otras vías en las cuales se obtienen marcadores mediante la determinación de parámetros de forma. Generalmente en la detección de parámetros de forma la transformada más utilizada es la de Hough, sin embargo, en otros estudios se demuestra que el método de la transformada Radon es equivalente, la diferencia reside simplemente en su interpretación computacional. Además, la transformada de Hough es más costosa computacionalmente que la transformada Radon (Ginkel M., 2004), (Tek, F.B, 2005).
En este trabajo se expone cómo obtener marcadores mediante la transformada Radon, que puedan ser utilizados para segmentar eritrocitos en imágenes de extendidos delgados de sangre periférica teñida con Giemsa aplicando la transformada watershed.
MATERIALES Y MÉTODOS
En el procesamiento digital de imágenes se han implementado diferentes métodos para la detección de marcadores basados en morfología matemática, lógica difusa, etc. Para obtener marcadores en imágenes de microscopía celular nos hemos basado en la propiedad de la transformada Radon ante estructuras circulares. Partiendo de una imagen de microscopia celular de glóbulos rojos, el primer paso es detectar los bordes de cada célula, los cuales se aproximan a una circunferencia. A esta imagen con bordes detectados se le aplica la transformada Radon. El siguiente paso es aplicar un filtrado adaptado con filtro de función tipo "herradura de caballo" y un radio específico a cada una de las proyecciones de la transformada Radon, y después reconstruir la imagen mediante la transformada reversa de Radon, lo cual da como resultado elevaciones máximas en presencia de circunferencias (Peng. H, 2008).
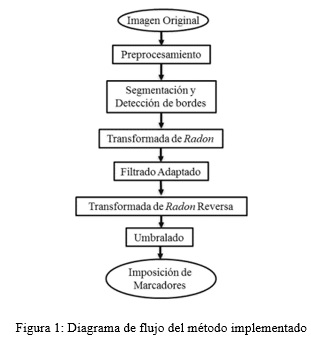
La Figura 1 muestra el diagrama de flujo de nuestro procesamiento.
Para mostrar por qué se trabaja con una imagen con bordes detectados puede utilizarse el siguiente ejemplo donde se observa una imagen de tres figuras geométricas, un cuadrado, un triángulo y un círculo, todos con semejante área. En la Fig. 2 a) se presenta la imagen con intensidad cero en el fondo y las figuras geométricas con intensidad uno. En la Fig. 2 b) se muestra la misma imagen después de realizarle cada uno de los pasos y por último reconstruirla con la transformada Radon reversa. Se puede observar cómo el círculo es resaltado por encima de las demás figuras geométricas, solo que no con una diferencia tan amplia como cuando se aplica el mismo procedimiento, ahora tomando la misma imagen y detectándole primeramente los bordes como muestra la Fig. 3.
Podemos observar en Fig. 3 a) los bordes detectados para cada figura geométrica y en b) como es realzado el pico que representa la circunferencia muy por encima de los demás objetos de la imagen.
A. Transformada de Radon directa
La transformada Radon bidimensional (RT-2D) continua es la integral de una función sobre un conjunto de rectas. Una recta p = xcos(θ) + ysen(θ) es el ángulo que forma el eje x con el vector posición del punto de la recta más cercano al origen. Las coordenadas de una imagen son usualmente positivas con el origen en su esquina superior izquierda; no obstante, para el cálculo de la RT -2D el origen debe desplazarse al centro de la imagen, lo que involucra un desplazamiento espacial. La transformada se presenta en la ecuación (1).
![]()
La transformada Radon (Peng. H, 2008), calcula las integrales de líneas de múltiples fuentes a lo largo de rayos paralelos que atraviesan el objeto, en este caso la imagen, en una cierta dirección. Para representar una imagen, toma múltiples proyecciones de rayos paralelos, a diferentes ángulos, rotando la fuente alrededor del centro de la imagen.
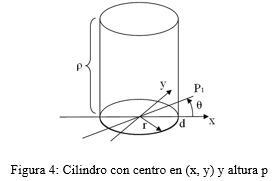
Para ver cómo funciona esta transformada ante estructuras circulares se explicará su comportamiento ante un cilindro como estructura teórica semejante a un eritrocito. El cilindro expresado por la función ![]() centrada en el origen (x,y) con simetría circular y altura
centrada en el origen (x,y) con simetría circular y altura ![]() se muestra en la Fig. 4; para el caso que tenga un soporte d positivo en el plano (x,y) puede representarse si su radio satisface |r| < d mediante
se muestra en la Fig. 4; para el caso que tenga un soporte d positivo en el plano (x,y) puede representarse si su radio satisface |r| < d mediante
![]()
Por tanto, la transformada Radon en un ángulo dado para un cilindro se define a partir de (1) y (2) en la ecuación (3).
![]()
El resultado obtenido en (3) se denomina ¨herradura de caballo”.
Como se analizó anteriormente la transformada Radon resalta con más claridad las estructuras en forma de circunferencia que en forma de disco. Por tanto, la función de una circunferencia se representa mediante la siguiente ecuación:
![]()
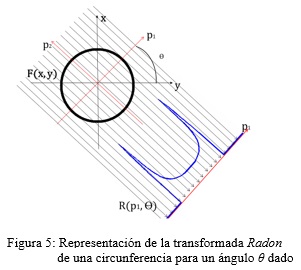
Para cualquier ángulo la transformada Radon de una circunferencia se comporta como una "herradura de caballo" invertida. El conjunto de las proyecciones de la transformada Radon directa para múltiples direcciones, 0 ≤ θ ≤ 180 grados, es el sinograma.
En la aplicación práctica para imágenes digitales la transformada Radon no se aplica en su forma continua. Los rayos paralelos que atraviesan la imagen a todo lo largo de cualquier proyección, son un número finito, ya que los sensores prácticos en las cámaras digitales son de espacio discreto. Además, los incrementos de los ángulos de giro θ también son discretos, como se puede observar en la Fig. 5. Por esta razón la transformada Radon se aplica en el espacio discreto. La cantidad de proyecciones y ángulos dependen de las características de la imagen u objeto a reconstruir y ningún autor define una cantidad fija. En el espacio discreto 2D la proyección de una imagen es la sumatoria de todos sus píxeles en un ángulo dado. Para un sistema de coordenadas [n1 , n2], definido por un ángulo θ, la transformada Radon a lo largo del eje n1 es la sumatoria de todos sus píxeles, definido en la ecuación (5).
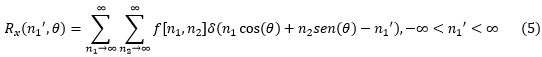
Para la implementación de la transformada Radon se utilizó la función proveniente del toolbox de Matlab para Procesamiento Digital de Imágenes (Image Processing Toolbox), radon, la cual calcula las proyecciones de la imagen a lo largo de direcciones paralelas específicas. En este trabajo se utiliza la opción de la transformada Radon con haces paralelos y no divergentes (fan). La función radon, como está en el espacio discreto, calcula la sumatoria de los píxeles a lo largo de caminos paralelos, o rayos (beams), en determinada dirección. Para representar una imagen, toma múltiples proyecciones de la misma en forma de haz, rotando la fuente diferentes ángulos alrededor del centro de la imagen (MathWorks, 2010). La misma tiene la siguiente sintaxis:
[R,xp] = radon(I,θ) (6)
En (6) R devuelve la transformada Radon de una imagen I en el ángulo θ. En caso de que θ sea un vector de ángulos, será una matriz denominada sinograma donde cada una de sus columnas representa la transformada de cada ángulo, teniendo tantas columnas como ángulos se quiera. Por lo general, y en este trabajo se emplea así, se toman los ángulos de 0 a 179 grados con incrementos de 1 grado, ya que para los demás ángulos se comporta de forma simétrica respecto al eje de las abscisas. El ángulo 180 no se incluye debido a la propiedad de la simetría de la transformada Radon.
B. Implementación del filtro adaptado
Un filtro adaptado es un sistema lineal e invariante cuya función principal es detectar la presencia de una señal conocida, o referencia, dentro de una señal recibida. La señal a la salida del filtro será la correlación de la señal de referencia (función del filtro) con la señal desconocida.
Para cada ángulo de rotación θ la proyección del cilindro sobre el eje p es la función "herradura de caballo", debido a la simetría del cilindro y a que este se encuentra centrado en el origen de (x,y). Para la construcción del filtro se realizó primeramente el cálculo matemático, el cual se explica a continuación.
En el plano (x,y) un cilindro de soporte d centrado en el origen sería como se presenta en la Fig. 6 a), y su proyección para cada ángulo ![]() en la Fig. 6 b).
en la Fig. 6 b).
Por ejemplo, para θi = 0 en cada punto pi la altura de ![]() es la cuerda de cada vertical con x, lo que coincide con el doble de la altura medida desde el eje x
es la cuerda de cada vertical con x, lo que coincide con el doble de la altura medida desde el eje x
2d = 2r (7)
El punto pi constituye la apotema de la circunferencia. Basado en conocimientos de trigonometría elemental, la longitud de la cuerda que pasa por el punto pi, en función del largo de la apotema, siendo el valor pi el lado de la apotema, es
![]()
Por tanto, conociendo la cuerda puede calcularse la apotema (p).
Para una estructura circular con un radio conocido r0 la construcción del filtro se obtendría a partir de las proyecciones correspondientes a cada ángulo (Peng. H, 2008). Por lo que se demostró anteriormente es necesario trabajar con imágenes donde los objetos que se quieren resaltar estén representados como circunferencias. La transformada Radon de una circunferencia es similar a la función “herradura de caballo”, pero invertida como se mostró anteriormente en la Fig. 5. La solución de la transformada Radon de una función circular para cualquier ángulo dado, (Peng. H, 2008) es:

Sustituyendo (7) en (10):

Un paso muy importante para que el algoritmo desarrollado dé como resultado picos en el centro de cada objeto que detecte como circunferencia, es la etapa de filtrado. Para realzar los marcadores correspondientes a circunferencias en la imagen final es necesario filtrar cada una de las proyecciones de la transformada Radon con un filtro adaptado. Posteriormente se reconstruye la versión de la imagen con la transformada Radon reversa. El filtro adaptado debe tener la forma de la transformada Radon de una circunferencia, la cual responde a la función "herradura de caballo" invertida dada por (11).
Antes de la construcción del filtro adaptado es necesario conocer el diámetro de una de las células, y a partir del mismo determinar el del filtro. Este diámetro se calculó de forma automática. Para ello se toma la máscara binaria obtenida de la imagen original. En esta imagen se encuentran elementos con aéreas más pequeñas que la de las células, comportándose como ruido y otros más grandes que son las células aglomeradas. Es necesario eliminar la mayor parte de las estructuras indeseadas, para ello se realiza una apertura morfológica con un disco de radio 20 píxeles con fines de suavizado. Se escoge un disco de este tamaño ya que el radio promedio de un eritrocito para las imágenes en cuestión es superior a los 50 pixeles. A partir de la máscara limpia de ruido se calcula el área de cada componente con la función regionprops y se obtiene un vector de áreas.
Seguido se calcula la mediana de este vector para garantizar que el área que se escoja pertenezca a una célula y no a un objeto ruidoso que no se eliminó o a un aglomerado. Suponiendo las células como un círculo y conociendo su área se calcula el diámetro despejando en la función de área de una circunferencia.
Para detectar las circunferencias es necesario aplicar un filtrado a cada una de las proyecciones de la transformada Radon, como ya se había mencionado. Para el filtrado se utilizó la función imfilter, con la siguiente sintaxis:
![]()
Donde R es la imagen a la cual se le aplicó la transformada Radon, filt es el filtro adaptado calculado y Rf es una matriz donde cada columna representan las proyecciones de Radon en cada ángulo, pero filtradas.
Para ver la función del filtro en la Fig. 7 a) se observa una imagen con cinco circunferencias y enFig. 7 b) la proyección de 45° de la transformada Radon. Al filtrar esta proyección con un filtro adaptado, Fig. 7 c), se puede observar como el mismo realza las estructuras que tengan su forma en la Fig. 7 d).
C. Transformada Radon reversa
Johann Radon demostró matemáticamente que es posible recuperar una función de dos variables si se conocen las integrales de la misma en todas las líneas del plano. Este resultado equivale a que se puede reconstruir la imagen de un objeto bidimensional si se tienen suficientes proyecciones del objeto en 180°.
El Teorema de la Proyección (Jain A.K, 1989) es un resultado fundamental, pues demuestra que a partir de suficientes proyecciones se puede conseguir una aproximación suficientemente buena de
f´(x, y), lo cual trae consigo poder reconstruir f(x, y). Si tal reconstrucción es posible, debe existir una forma de expresar la transformada inversa de Radon, pues dicha operación consiste en recuperar la imagen f(x, y) a partir de sus proyecciones.
La recuperación mediante retroproyección es el aporte de cada proyección sobre los píxeles de la imagen desde su ángulo de adquisición entre el número de proyecciones. Para la reconstrucción de la imagen x[n1 , n2], donde Rx(n1', θ) es su sinograma en las direcciones 0 ≤ θ < 180, puede calcularse su retroproyección mediante la ecuación (13).
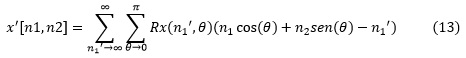
La principal dificultad de la retroproyección es que tras su única iteración no alcanza la solución esperada, por tanto, es necesario mejorar el resultado. La retroproyección filtrada es la variante mejorada, la misma realza las altas frecuencias mediante un filtrado paso-alto de las proyecciones del sinograma previo a la reconstrucción. Para ello es necesario utilizar el teorema de línea central de Fourier de la transformada Radon.
El problema de utilizar el teorema de la línea central de Fourier como método para recuperar la imagen a partir de sus proyecciones radica en el muestreo no uniforme. Una vez filtrado paso-alto el sinograma en el dominio de la frecuencia se retorna al dominio del espacio mediante la transformada de Fourier inversa 1D de sus columnas.
El método de retroproyección filtrada es el más utilizado en tomografía para reconstrucción tanto en imágenes de transmisión (ej. Tomografía computarizada) como de emisión (ej. Tomografía por emisión de positrones, PET) y es actualmente el algoritmo recomendado por la Asociación Nacional de la Industria Eléctrica (NEMA por sus siglas en inglés) debido a su bajo costo computacional, velocidad y sencillez.
La transformada Radon reversa se aplica después de pasarle el filtro con forma “herradura de caballo” invertida a cada una de las proyecciones de la transformada Radon. El objetivo no es recuperar la imagen exactamente como estaba al principio, sino que la misma tenga las células resaltadas con picos en el centro.
La reconstrucción de la imagen por este método está implementada en Matlab con la función iradon. La sintaxis de la misma es:
![]()
En (14) IR es la imagen reconstruida, Rf serán las proyecciones de la transformada Radon, en nuestro caso serán las proyecciones después de filtradas con el filtro adaptado, y θ es el mismo vector de ángulos que tiene como argumento la función radon.
También se le pasa como argumento otros dos parámetros adicionales. Primero el tipo de interpolación, utilizado en el algoritmo de retroproyección (back projection) para convertir de coordenadas radiales a coordenadas rectangulares. Segundo un filtro paso-alto tipo rampa en frecuencias que se aplica en este algoritmo para realzar los detalles a ser reconstruidos. La función iradon usa el algoritmo de reconstrucción retroproyección filtrada (filtered back projection). El filtro que aplica el algoritmo es diseñado directamente en el dominio de la frecuencia y multiplicado por la transformada rápida de Fourier (FFT por sus siglas en inglés) de las proyecciones. Las proyecciones son rellenadas con ceros para evitar el aliasing en el dominio espacial y acelerar la FFT.
Tras un proceso devaluación, el método de interpolación que mejor resultados ofreció fue interpolación nearest (vecinos más cercanos) ya que tiene menor costo computacional que todas los demás y porque de acuerdo a la evaluación estadística los resultados son semejantes. El tipo de filtro escogido es el Ram-Lak (filtro rampa) que al compararlo con los demás computacionalmente las diferencias no son significativas, pero los marcadores obtenidos son mejores en cuanto a posición y cantidad, por sus características de resaltar las altas frecuencias.
Al aplicarle esta función al sinograma filtrado con el filtro adaptado, el cual realza las formas donde hay una estructura similar a la “herradura de caballo” invertida, y reconstruir la imagen con la transformada Radon reversa, obtendremos a la salida una imagen con elevaciones en la posición central de todos los elementos de la imagen que se hayan detectados como circunferencias. En la Fig. 8 se muestra un ejemplo de cómo al aplicar este método las células son resaltadas en el centro. En Fig. 8 a) se muestra la imagen de glóbulos rojos, en Fig. 8 b) se muestra la imagen después de aplicarle la transformada Radon directa, filtrar cada una de las proyecciones de la misma y recuperarla con la transformada Radon reversa y en Fig. 8 c) se muestra topográficamente para visualizar mejor los picos.
D. Umbralado y detección de marcadores
Después de obtener la imagen reconstruida mediante la transformada Radon reversa es necesaria la búsqueda de un umbral, como se muestra en la Fig. 9 a), para binarizar la misma y obtener la imagen marcador. Los picos por encima de un nivel de umbral serían los marcadores y todo lo demás el fondo en negro, Fig. 9 b).
La obtención de este umbral de forma automática que funcione para todas las imágenes y obtenga solo los picos que representan centros de células no es simple. Como se puede observar en la Fig. 8 c) y Fig. 9 a), los picos que representan centros de células no tienen la misma altura, dependen del tamaño de la célula y la posición que ocupe la misma en la imagen.
La detección de un umbral adaptativo podría ser la solución, pero no solamente binariza los picos que marcan la posición central de las células, también lo hace con los bordes de las células que están levemente resaltados. El histograma de la imagen recuperada no es bimodal, tiene un solo lóbulo, y el cálculo del umbral por el método de Otsu no ofrece una solución para el problema. Para calcular el umbral de forma automática y que el mismo se comporte diferente según la imagen a tratar se tuvo en cuenta la forma de las mismas y cómo se comporta su histograma.
El histograma de una imagen por el eje de las abscisas representa la distribución de grises y por el eje de las ordenadas la cantidad de píxeles presentes en la imagen de un nivel de intensidad determinado. En la imagen obtenida a la salida de la transformada Radon reversa los picos que representan los centros de los eritrocitos, son los que tiene niveles de intensidades más cercanos a uno. La probabilidad de ocurrencia de los niveles de intensidad que representan los picos es muy baja.
Analizando las imágenes recuperadas y sus histogramas, Fig. 10 a), se pudo observar que la distribución de píxeles representadas en el lóbulo del mismo, representa completamente el fondo de la imagen, y no los picos que sobresalen en el centro de las células. La representación de los picos en el histograma son los píxeles que se encuentran desde el final del lóbulo visible hasta el final de histograma.
En la imagen recuperada, erróneamente se producen picos que no representan el centro de ninguna célula. Para determinar un umbral que fuese automático y en la medida de lo posible se adaptara a cada una de las imágenes, determinando todos los centros de células y discriminando aquellas elevaciones que no son de interés, se tomó como criterio adoptar un valor fijo para el eje de las ordenadas, y que en dependencia del mismo se calculará el umbral en las abscisas.
Para ello se hizo un ciclo while que recorriera el histograma de mayor a menor intensidad, y cuando llegara a una cantidad de píxeles dada se detuviera y estableciera el umbral. Probando para el conjunto de las 20 imágenes diferentes utilizadas en la evaluación, con 1120 células, se observó que fijando una cantidad cualquiera de probabilidad de ocurrencia de píxeles entre 100 y 200 (eje de las ordenadas), el cálculo del umbral no varía significativamente para una misma imagen (eje de las abscisas), y los resultados son los esperados. Las líneas en rojo, Fig. 10 b), prueban esta afirmación. Además, el cálculo del umbral se adapta a las veinte imágenes. Se tomó 150 como la cantidad de píxeles fijas, representada por las líneas verdes de la Fig. 10 b).
Como se puede observar en la Fig. 9 b) puede existir más de un marcador dentro de una célula. Para solucionar este problema se realizó una dilatación sobre la imagen binaria obtenida al aplicar el umbral mencionado en el párrafo anterior, con un disco de radio veinte, para unir todos los píxeles dentro de una misma célula y representarlo con un solo marcador. Con el objetivo de que los marcadores fuesen todos del mismo tamaño se aplicó la función bwmorph con la sintaxis que muestra la ecuación (15)
![]()
Otro problema que puede presentarse es que existan marcadores en el fondo de la imagen donde no existen células. Para eliminar este problema se realizó un AND lógico entre la imagen obtenida y la binaria limpia de ruido.
E. Evaluación estadística
Después que el algoritmo marque las células, el método propuesto debe ser evaluado estadísticamente. Un análisis estadístico comúnmente empleado para evaluar la calidad de métodos de procesado de imágenes es el cálculo de indicadores de desempeño. Ejemplo de los mismos son sensibilidad (Se), especificidad (Sp), predictividad positiva (PP o P+), medida-F, etc (Nasir A.S.A, 2012), (Nasir A.S.A, 2013), (Popovic A., 2007). Para evaluar el método se tomaron veinte imágenes con un total de 1120 eritrocitos, las cuales fueron marcadas por cinco expertos y tomando como ground-truth aquellos eritrocitos en los que coincidieran al menos tres de los expertos.
En este trabajo se adaptan estas medidas con vistas a la evaluación de los algoritmos marcadores de eritrocitos. Los verdaderos positivos son células marcadas por el experto que el software marco como célula, los falsos positivos donde marcó el software que no marcó el experto, los falsos negativos son las marcadas por el experto y no por el software y los verdaderos negativos son las células no marcadas por el experto y tampoco por el software.
RESULTADOS Y DISCUSIÓN
El resultado final del algoritmo desarrollado en este trabajo es una imagen binaria donde el fondo es de intensidad cero y en la posición de los eritrocitos puntos con intensidad uno. En la Fig. 11 se observan dos imágenes con marcadores de color verde. La Fig. 11 a) es el ground-truth, la cual se le impusieron los marcadores de forma manual y la Fig. 11 b) imagen marcada por el algoritmo implementado, lo cual es la superposición de la imagen resultante del marcado con la imagen original.
En este ejemplo, se puede observar cómo son marcadas por el software la mayoría de las células consideradas por el experto como contables. Encerrados en una circunferencia negra se puede observar algunos eritrocitos aglomerados, los cuales son marcados de forma independiente. En algunos casos como los señalados con flechas rojas el software impone una sola marca donde los expertos determinan que existen dos eritrocitos, lo cual puede ser debido a que están demasiado solapados. En otros casos, señalados con flecha azul, hay eritrocitos con dos marcadores. La causa de que el algoritmo ofrezca como resultado más de una marca por célula es debido a la calidad de la imagen a la cual se le aplica la transformada Radon directa. Esto trae como resultado que al recuperar la imagen con la transformada Radon reversa exista más de un pico por eritrocito. La flecha amarilla señala un ruido en el fondo de la imagen el cual no fue marcado por el algoritmo.
A. Valor medio y desviación estándar de los índices
Para analizar el comportamiento del método planteado en la Tabla 1 se muestran la media y la desviación estándar de los índices exactitud, sensibilidad, predictividad positiva y medida-F para los 1120 eritrocitos. La predictividad positiva y la medida-F se representan en por ciento.
Cada uno de estos índices es calculado para las veinte imágenes, y después se le calcula la media, la cual se observa en la Tabla 1. La desviación estándar (Std), es una medida del grado de dispersión de los resultados del índice con respeto a su media. Cuanto mayor sea este valor mayor será la variabilidad del índice ante cada una de las muestras, en este caso las marcas en los eritrocitos.
La exactitud es la probabilidad de que los resultados del software sean completamente verdaderos, nos da una medida de que tan exacto es a la hora de marcar sin cometer errores. Benson. C. C. (Benson. C, 2015), calcula valores de exactitud para imágenes médicas por tres métodos. El método basado en clustering le da como resultado un 85 %, el basado en umbralado un 77,5 % y el de morfología matemática 93.75%. Para las imágenes que nos ocupan los métodos basados en morfología matemática no son eficientes sobre todo a la hora de marcar los eritrocitos que se encuentran aglomerados.
La sensibilidad es la probabilidad de que lo marcado por el experto como eritrocito el algoritmo también lo marque, y puede tomarse como el porciento de marcado. El índice predictividad positiva se presenta como la probabilidad de que los eritrocitos detectados realmente lo sea, lo cual da una medida del porciento marcado por el algoritmo con respecto al marcado por los expertos. Como se puede observar en la tabla, este índice es de 97.3724 %, lo cual da una medida de que el software impone menos de tres marcas cada cien donde no debía. La medida-F es un índice que expresa la probabilidad de que el algoritmo marque los eritrocitos señalados por el experto sin cometer errores. Este índice, como se observa en la Tabla 1 está por encima del noventa por ciento, y además con una desviación estándar menor que cinco.
CONCLUSIONES
La aplicación de la transformada Radon es muy útil para marcar como independientes los eritrocitos que están solapados, siempre y cuando no sea en la mayor parte de su área.
El algoritmo deja de marcar en ocasiones eritrocitos que visualmente no se consideran que tengan dificultad para colocar marcadores sobre los mismos. Ello es debido a que en la segmentación estos no quedan de forma circular y a la hora de aplicar el filtrado adaptado al sinograma de la transformada Radon no logran ser realzados lo suficiente.
Otra causa de por qué los algoritmos dejan de marcar eritrocitos es el umbralado de la imagen resultante de la transformada Radon reversa. Los picos que resaltan en esta imagen deberían ser idealmente del mismo tamaño, pero no es así, por lo que a la hora de determinar un umbral los mismos pueden quedarse por debajo y ser eliminados en la imagen marcador.
El uso de la transformada Radon para determinar marcadores en imágenes de extendidos de sangre periférica ayuda a mejorar el conteo automático de eritrocitos por medio de una computadora y permite el marcado de los mismos para una posterior segmentación mediante la transformada de watershed.
REFERENCIAS BIBLIOGRÁFICAS
Benson. C. C, Kumar Rajamani and Lajish V. L. (September 2015). "A Review on Automatic Marker Identification Methods in Watershed Algorithms Used for Medical Image Segmentation." IJISET 2(9).
Ginkel, M.v., C.L.L. Hendriks, and L.J.v. Vliet, A short introduction to the Radon and Hough transforms and how they relate to each other. Quantitative Imaging Group Technical Report Series, 2004.
Jain, A.K, Fundamentals of Digital Image Processing, Prentice Hall, NJ, ISBN: 0-13-336165-9, 1989.
Maragos, P., R. W. Schafer, and M. A. Butt, Editors, Mathematical Morphology and its Application to Image and Signal Processing, Kluwer Academic Publishers, Boston, 1996.
MathWorks, Image Processing Toolbox™ 7, User’s Guide, 2010.
Nasir, A.S.A., M.Y.Mashor, and Z.Mohamed, Segmentation Based Approach for Detection of Malaria Parasites Using Moving K-Means Clustering. 2012.
Nasir, A.S.A., M.Y. Mashor., and Z. Mohamed., Colour Image Segmentation Approach for Detection of Malaria Parasites Using Various Colour Models and k-Means Clustering. Biology and Biomedicine, WSEAS Transactions on, 2013. 10(2): p. 41-56.
Peng, H. and R. Rao, A novel circle detection method using Radon Transform. 2008. Vol. 6813.
Popovic, A., et al., Statistical validation metric for accuracy assessment in medical image segmentation. Int J CARS, 2007. Vol. 2: p. 169–181.
Rocha, D. A. and C. S. Ferrer (2015). "Informe Mundial sobre la Malaria 2015: avanzando hacia su erradicación." 7/03/16, from http://www.madridsalud.es/temas/Informe_Mundial_sobre_la_Malaria2015.php.
Soille, P., Texture analysis, En: Morphological Image Analysis: principles and applications: Ch. 11, Second ed., P. Soille (ed.), Springer. 2004: Italy. 399.
Tek, F.B., Andrew G. Dempster, Izzet Kale Blood Cell Segmentation Using Minimum Area Watershed and Circle Radon Transformations in Mathematical Morphology: 40 Years On, S. Netherlands, Editor. 2005. p. 441-454.
Valdés, L. C. and J. V. L. Ginori (2010). "Evaluación de Alternativas Basadas en la Transformada de Distancia para la Segmentación de Imágenes de Objetos que se Solapan." International Conference of Computer Science and Informatics.
WHO, Basic malaria microscopy Part I. Learner's Guide. World Health Organization, 1991.
Recibido: 03/09/2016
Aceptado: 15/12/2016