My SciELO
Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO
Related links
-
 Similars in
SciELO
Similars in
SciELO
Share
Revista Cubana de Ciencias Informáticas
On-line version ISSN 2227-1899
Rev cuba cienc informat vol.11 no.2 La Habana Apr.-June 2017
ARTÍCULO ORIGINAL
Reparación de Data Warehouses con sentido semántico
Repairing Data Warehouses with semantic meaning
Raúl Arredondo1*, Luis Muñoz1
1Universidad de Los Lagos, raul.arredondo@ulagos.cl
*Autor para la correspondencia: raul.arredondo@ulagos.cl
RESUMEN
Un Data Warehouse (DW) es un almacén de datos que se modela utilizando el modelo multidimensional, el cual estructura la información a través de dimensiones y hechos. Una dimensión es un concepto abstracto que agrupa datos que comparten un significado semántico común, modelada mediante jerarquías de categorías, las que contienen elementos. Una dimensión es estricta si cada elemento de toda categoría tiene un único ancestro en cada categoría superior y homogénea si cada elemento tiene al menos un ancestro en cada categoría superior. Una dimensión puede volverse inconsistente con respecto a sus restricciones de integridad estrictas y homogéneas después de una actualización y cuando esto sucede la dimensión debe ser reparada. Una reparación es una nueva dimensión que satisface el conjunto de restricciones estrictas y homogéneas y se obtiene insertando y eliminando arcos entre elementos de las categorías. Si la dimensión se vuelve inconsistente luego de una única operación de reclasificación de elementos es posible computar una reparación, que contiene la actualización, en tiempo polinomial, sin embargo, esta reparación no garantiza la semántica de los datos. En este artículo se indican otra clase de restricciones que guían el proceso de reparación tales como restricciones de prioridad y seguras, nuevas heurísticas y una propuesta algorítmica que permitan encontrar una reparación con correcto sentido semántico, sin embargo, es posible no encontrar una reparación que garantice la semántica de los datos.
Palabras clave: Data Warehouse, inconsistencia, restricciones estrictas, restricciones homogéneas, heurísticas.
ABSTRACT
A Data Warehouse (DW) is a data repository that is modeled using the multidimensional model, which structures the information according to dimensions and facts. A dimension is an abstract concept that brings together data that share a common semantic meaning, modeled by category hierarchies, which contain elements. A dimension is strict if all category each element has a unique ancestor in each upper and covering category if each element has at least one ancestor each higher category. A dimension can become inconsistent with respect to their strictness constraint and covering integrity after update operations and when this happens the dimension must be repaired. A repair is a new dimension that satisfies the set of strictness and covering constraints and that is obtained inserting and deleting arcs between elements of the categories. If the dimension becomes inconsistent after a single operation reclassification of items it is possible to compute a repair, in polynomial time, but this repair does not guarantee the semantics of the data. In this article different kind of restrictions that guide the repair process such as priority and safe constraints, new heuristics and a algorithmic approach that allow to find a repair with a correct semantic meaning, however, it is possible not to find a repair that guarantees the semantics of the data.
Key words: Data Warehouse, inconsistency, stricness constraints, covering constraints, heuristics.
INTRODUCCIÓN
Un Data Warehouse (DW) es un conjunto de datos orientados a temas específicos, integrados, que se acumulan en el tiempo, para apoyar la toma de decisiones (Chaudhuri and Dayal, 1997), los cuales son integrados de distintas fuentes. Éstos son modelados bajo un enfoque multidimensional a través de dimensiones y hechos. Las dimensiones reflejan la forma en que se organizan los datos y se modelan como jerarquías de elementos, llamadas esquemas jerárquicos donde cada elemento pertenece a una categoría. Los hechos corresponden a eventos que se asocian generalmente a valores numéricos llamados medidas, y hacen referencia a elementos de una dimensión (Hurtado et al., 1999).
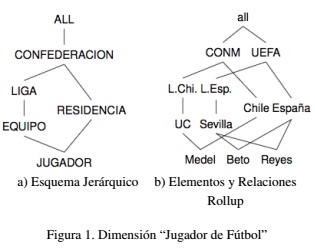
Como un ejemplo, la Figura 1(a) muestra un esquema jerárquico de la dimensión “Jugador de Fútbol”, mientras que la Figura 1(b) muestra los elementos y como éstos se relacionan, es decir sus relaciones rollup (Hurtado et al., 1999). Aquí se señala que CONM (que significa CONMEBOL) y UEFA son elementos de la categoría CONFEDERACION, L. Chi. (Liga Chilena) y L.Esp. (Liga Española) son elementos de la categoría LIGA, UC (Universidad Católica) y Sevilla son elementos de la categoría EQUIPO, Chile y España son elementos de la categoría RESIDENCIA y por último Medel, Beto y Reyes son elementos de la categoría JUGADOR (categoría inferior). La estructura jerárquica de las dimensiones permite el cálculo de consultas a diferentes niveles de granularidad, por ejemplo, en la dimensión indicada en la Figura 1(b) es fácil computar consultas agrupadas por JUGADOR, LIGA y así sucesivamente.
Es una práctica común en DWs utilizar los resultados precomputados en los niveles inferiores de jerarquía de la dimensión, para calcular resultados en niveles superiores (esto se llama sumarizabilidad (Hurtado et al., 2005), (Lenz and Shoshani, 1997)).
Para garantizar la sumarizabilidad, una dimensión debe satisfacer ciertas restricciones de integridad (Hurtado and Gutierrez, 2007). Primero, debe ser estricta, es decir que cada elemento de una categoría inferior esté relacionado con un único elemento en la categoría superior, y homogénea, es decir que cada elemento de una categoría inferior esté relacionado por lo menos con un elemento en las categorías superiores. Una dimensión es consistente si satisface todas sus restricciones de integridad, de lo contrario, es inconsistente (Caniupán et al., 2012).
Una dimensión puede volverse inconsistente con respecto a sus restricciones de integridad después de una reclasificación de elementos, que es una modificación a la relación rollup entre dos elementos, sobre todo para dimensiones cuyos esquemas jerárquicos cuentan con un nivel de conflicto (Caniupán and Vaisman, 2011), es decir, una categoría que es alcanzada desde la categoría inferior por caminos alternativos, como el esquema jerárquico de la Figura 1(a), donde la categoría CONFEDERACION es un nivel de conflicto.
De acuerdo a (Caniupán et al., 2012) una dimensión inconsistente debe ser reparada (corregida). A modo de ejemplo, la Figura 2(b) muestra una actualización en la dimensión “Jugador de Fútbol” (D) indicada en la Figura 2(a), es decir un cambio en la relación rollup entre elementos de las categorías JUGADOR y EQUIPO, ya que el elemento Medel se relaciona con Sevilla, en vez de UC. Después de esta actualización, la dimensión no satisface la restricción estricta JUGADOR → CONFEDERACION (la que establece que un jugador está asociado a una única confederación), ya que ahora el jugador Medel está asociado con dos elementos de la categoría CONFEDERACION, esto es con CONM a través de la categoría RESIDENCIA y con UEFA por las categorías EQUIPO y LIGA. Para resolver este problema, la dimensión necesita ser corregida.
MATERIALES Y MÉTODOS
El problema de reparación en bases de datos relacionales con respecto a un conjunto de restricciones de integridad (por ejemplo, dependencias funcionales y dependencias de inclusión) ha sido ampliamente estudiado en (Arenas et al., 1999; Arenas and Bertossi, 2003; Bravo and Bertossi, 2004; Bertossi, 2006; Lopatenko and Bertossi, 2006).
Si bien existen muchas formas de poder representar un DW usando modelos relacionales (esquema en estrella o esquema copo de nieve (Chaudhuri and Dayal, 1997), (Anisimov, 2003)), no es posible usar las técnicas de reparación para bases de datos relacionales para calcular las reparaciones de DWs.
Esto se debe a que en el enfoque relacional, la inconsistencia de la base de datos se soluciona mediante la insersión, eliminación y actualización de tuplas e incluso alterando la dimensión (Kimball, 1996) y esto no coincide con el enfoque utilizado en DWs que modifica arcos entre elementos. En (Caniupán et al., 2012) se muestran varios ejemplos donde se puede concluir que es imposible codificar una dimensión multidimensional dentro de un esquema relacional de DW y obtener las mismas reparaciones minimales mostradas en (Caniupán et al., 2015) utilizando técnicas relacionales.
Una diferencia importante con respecto a las reparaciones relacionales es que en los DWs se utiliza una semántica de reparación basada en cardinalidad (Afrati and Kolaitis, 2009), (Bertossi, 2006), es decir, reducir al mínimo el número de cambios realizados en una dimensión, mientras que en el modelo relacional además de basarse en la cardinalidad, se puede reparar reduciendo al mínimo el conjunto de tuplas insertadas y eliminadas.
Una r-reparación minimal es una nueva dimensión que satisface su conjunto de restricciones de integridad la cual se obtiene desde la dimensión original aplicando eliminación e insersión de arcos entre elementos y en el caso general, encontrar una r-reparación minimal es NP-duro (Caniupán and Vaisman, 2011), sin embargo bajo ciertas condiciones, el cómputo de r-reparaciones puede hacerse en tiempo polinomial y para ello ya hay algoritmos procedurales que resuelven este problema (Caniupán et al., 2015).
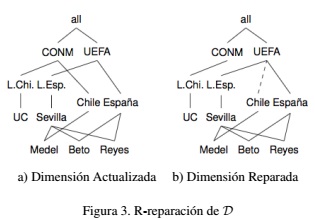
Como se señala en la Figura 3(b), la r-reparación computada por lo presentado en (Caniupán et al., 2015) es un cambio entre las categorías RESIDENCIA y CONFEDERACION ya que la relación rollup existente entre los elementos Chile y CONM es reemplazada por Chile y UEFA.
La Figura 3(b) es una r-reparación sintácticamente correcta de la dimensión D señalada en 3(a) ya que devuelve la consistencia a la dimensión, sin embargo, por la semántica y lógica de los datos, no tiene sentido que Chile se relacione con UEFA. Esto se debe a que UEFA es la confederación de fútbol que asocia a países de Europa y algunos países en controversia como Israel, mientras que CONM (CONMEBOL) agrupa a países de Sudamérica. Por esta razón, se han considerado señalar nuevas restricciones impuestas por el administrador del DW para obtener una r-reparación con correcto sentido semántico:
-
Restricciones seguras: Una restricción segura señala que el vínculo directo entre dos categorías no se debe modificar, es decir, que ninguna relación rollup que involucre a elementos de estas categorías puede alterarse aunque sea necesario hacer cambios para lograr la consistencia de una dimensión.
-
Restricciones con grado de prioridad: Un grado de prioridad es una constante real que oscila entre 0 y 1, la cual indica el grado de confianza que existe entre los vínculos di rectos entre dos categorías. Mientras la prioridad sea más cercana a 0, menos confiable es la relación que existe entre las categorías involucradas; contrariamente es el caso en que la prioridad sea más cercana al valor 1.
Cabe señalar que estas restricciones deben ser señaladas por el administrador del DW previo a ejecutar un proceso de reparación y que no son parte del esquema jerárquico de una dimensión.
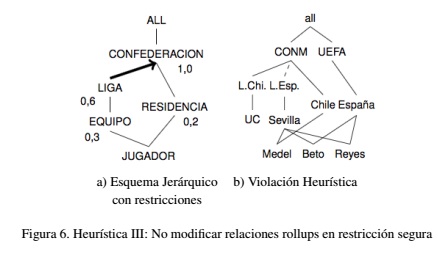
Como se indica en la Figura 4, se han denotado las siguientes restricciones con grado de prioridad:
-
Grado de prioridad entre las categorías RESIDENCIA y CONFEDERACION: 1,0
-
Grado de prioridad entre las categorías JUGADOR y RESIDENCIA: 0,2
-
Grado de prioridad entre las categorías JUGADOR y EQUIPO: 0,3
-
Grado de prioridad entre las categorías EQUIPO y LIGA: 0,6
Adicionalmente, en la Figura 4, se ha denotado la restricción segura entre las categorías LIGA y CONFEDERACION (señalada con una flecha).
A modo de análisis, las relaciones rollups entre RESIDENCIA y CONFEDERACION son muy confiables, es decir, históricamente se han hecho pocos cambios entre estas categorías. Sin embargo, las relaciones rollups entre JUGADOR y RESIDENCIA han sufrido diferentes actualizaciones en el transcurso del tiempo.
Para poder computar una r-reparación con correcto sentido semántico en tiempo polinomial se ha redefinido el proceso de reparación considerando las siguientes heurísticas:
(i) No generar nuevas inconsistencias en el proceso de reparación: esta heurística se encuentra definida en (Caniupán and Vaisman, 2011).
(ii) Elegir en lo posible, los cambios donde el rollup tenga menor grado de prioridad: Sea el esquema jerárquico, las restricciones con grado de prioridad y la restricción segura mostrada en la Figura 5(a) y la actualización señalada en la Figura 2(b).
Esta heurística permite orientar la búsqueda de cambios en las relaciones rollups donde las categorías posean el menor grado de prioridad posible. Como se señala en la Figura 5(c), la modificación esperada sea en una relación rollup entre las categorías JUGADOR y RESIDENCIA, puesto que tienen el menor grado de prioridad según el administrador del Data Warehouse (0,2).
La r-reparación computada utilizando el algoritmo mostrado en Caniupán et al. (2015), ya que este algoritmo realiza los cambios entre las categorías RESIDENCIA y CONFEDERACION, que según el administrador del Data Warehouse tiene prioridad 1,0.
(iii) No modificar relaciones rollup en la(s) restriccion(es) segura(s):Sea el esquema jerárquico, las restricciones con grado de prioridad y la restricción segura mostrada en la Figura 6(a) y la actualización señalada en la Figura 2(b).
La Figura 6(b) indica un mal cambio, puesto que no se pueden modificar las relaciones rollups existentes entre las categorías LIGA y CONFEDERACION puesto que es una restricción segura. Además, si se quisieran realizar cambios entre estas categorías, nuevos elementos se ven involucrados en la inconsistencia, violando la heurística (i) definida en Caniupán and Vaisman (2011).
A continuación se presenta una propuesta algorítmica para poder computar, en lo posible, una r- reparación con correcto sentido semántico:
Para explicar el funcionamiento del algoritmo 1 se analizará el esquema jerárquico mostrado en la Figura 1(a), la actualización señalada en la Figura 2(b) y las restricciones impuestas por el administrador del DW (grados de prioridad y restricciones seguras) indicados en la Figura 4. Para ello se detalla el valor de las variables de entradas del algoritmo 1:
-
D: es la dimensión con la que se trabajará, en este caso “Jugador de Fútbol”.
-
R: es la reclasificación que originó la inconsistencia con respecto a sus restricciones de integridad. En este caso, es el cambio en la relación rollup entre Medel y UC, por la relación rollup entre Medel y Sevilla.
En la línea 1 del algoritmo 1 se obtienen todos los elementos que se volvieron inconsistentes con respecto a sus restricciones de integridad representados en caminos, almacenando sus grados de prioridad (por notación, la restricción segura tendrá el valor 2,0 y el elemento perteneciente al nivel de conflicto tendrá el valor 1,5), en esta situación:
-
Medel(0,3) → Sevilla(0,6) → L.Esp.(2,0) → UEFA(1,5) →
-
Medel(0,2) → Chile(1,0) → CONM(1,5) →
Como no hay más elementos en la categoría inferior (JUGADOR) involucrados en la inconsistencia, se procede a ejecutar las líneas 2 y 3 del algoritmo 1, en las cuales se obtienen los elementos en el nivel de conflicto que están involucrados en la inconsistencia, en este caso:
-
UEFA que será almacenada en la variable var1 (elemento afectado por la reclasificación).
-
CONM que será almacenada en la variable var2 (elemento no afectado por la reclasificación).
En las líneas 4 y 5 de este algoritmo, se procede a obtener las mínimas prioridades que alcanzan los caminos que llegan a los elementos en el nivel de conflicto involucrados en la inconsistencia con respecto a sus restricciones de integridad, lo que en el ejemplo mostrado es:
-
Mínima prioridad en la ruta entre Medel y UEFA es 0,3. Este valor es almacenado en la variable p_var1.
-
Mínima prioridad en la ruta entre Medel y CONM es 0,2. Éste es almacenado en la variable p_var2.
El ciclo descrito entre las líneas 6 y 20 del algoritmo 1 se ejecutará hasta que no hayan inconsistencias con respecto a sus restricciones de integridad (líneas 7 a la 18), o hasta que no encuentre una r-reparación con correcto sentido semántico (líneas 19 y 20). Siempre se buscará hacer los cambios en las relaciones rollups con menor grado de prioridad y para este ejemplo se buscará un cambio en la ruta cuyo último elemento es CONM, puesto que la mínima prioridad existente en la ruta entre Medel y CONM (0,2) es menor que la mínima prioridad existente entre Medel y UEFA (0,3), es decir, se ejecutarán las instrucciones entre las líneas 12 y 16 de este algoritmo. Si se da una situación contraria a la descrita anteriormente, se ejecutarán las instrucciones entre las líneas 7 y 11 del algoritmo 1.
Si no se encuentra un cambio que retorne la consistencia a la dimensión (línea 15 del algoritmo 1 para este caso), se procederá a buscar el siguiente grado de prioridad mínimo existente en la ruta analizada (línea 16 del algoritmo en esta situación). De lo contrario, se buscará un nuevo elemento en la categoría inferior involucrado en la inconsistencia (líneas 17 y 18 del algoritmo 1), situación que no se da en este escenario.
El algoritmo 2 trata de computar los cambios con correcto sentido semántico que devolverán la consistencia a la dimensión. Las variables de entrada a este algoritmo dependerá de las líneas 9 y 14 del algoritmo 1. Para este ejemplo, se ejecutó la línea 14 del algoritmo 1 y se tienen los siguientes resultados:
-
D es la dimensión con la que se trabajará, en este caso “Jugador de Fútbol”
-
R es la reclasificación que originó la inconsistencia con respecto a sus restricciones de integridad. En este caso, es el cambio en la relación rollup entre Medel y UC, por la relación rollup entre Medel y Sevilla.
-
inc representa a todos los elementos involucrados en la inconsistencia con respecto a sus restricciones de integridad.
-
v1 es el elemento en la categoría nivel de conflicto que será relacionado con todos los elementos involucrados en la inconsistencia, en este escenario UEFA.
-
v2 es el elemento en la categoría nivel de conflicto que no tendrá relación con todos los elementos involucrados en la inconsistencia, en este ejemplo CONM.
En este caso, para cada ruta de un elemento en la categoría inferior involucrado en la inconsistencia con respecto a sus restricciones de integridad (líneas 1 a la 17 del algoritmo 2), se busca la ruta donde se encuentre el elemento v2 (líneas 2 y 3 del algoritmo 2), en este caso:
-
Medel(0,2) → Chile(1,0) → CONM(1,5) →
Posteriormente, se obtiene el elemento e1 en la ruta donde se encuentre la menor prioridad, que no deshaga la actualización que originó la inconsistencia y que no origine nuevas inconsistencias en el proceso de reparación (función elemento_min_prio(), línea 4), que en este ejemplo es Medel. En caso de no encontrar un elemento e1, el algoritmo 2 retorna 0 al algoritmo 1, para que continúe su ejecución (líneas 5, 14 y 15 del algoritmo 2).
En la línea 6, se obtiene la categoría (C1) a la que pertenece el elemento e1, que según este ejemplo Medel pertenece a la categoría JUGADOR. Entre las líneas 7 y 8, se obtienen la categoría superior (C2) y el elemento en esta categoría (e2), que permitirá computar la reclasificación de elementos que devolverá la consistencia a la dimensión, que para este ejemplo (C2) corresponde a la categoría RESIDENCIA y e2 al elemento España. De no existir estos valores, el algoritmo 2 retorna 0 al algoritmo 1, para que continúe su ejecución (líneas 12 y 13 del algoritmo 2). En definitiva, obtener una r-reparación con correcto sentido semántico, se compone de dos procesos:
-
El proceso que obtiene los elementos que son inconsistentes con respecto a restricciones estrictas y permite analizar las posibles variantes de reparación (algoritmo 1).
-
El proceso que se encarga de computar los cambios aplicando las heurísticas mencionadas anteriormente:
-
No generar nuevas inconsistencias en el proceso de reparación.
-
Elegir en lo posible, los cambios donde el rollup tenga menor grado de prioridad.
-
No modificar relaciones rollup en la(s) restriccion(es) segura(s).
-
Sea n el número máximo de elementos de una categoría, r el número máximo de relaciones rollups entre dos categorías, y ms el número de restricciones estrictas. El costo de comprobar si una restricción estricta ci → cj es violada por una dimensión D es O(r2) ya que la relación ![]() es de tamaño O(r) y se necesita comparar cada tupla en ella con todas sus tuplas. A pesar de que en el peor de los casos r es O(n2), se espera que r sea O(n) ya que en general el número de violaciones de una restricción es pequeña, y por lo tanto la mayoría de los elementos en una categoría se relacionan con un único elemento en una categoría superior.
es de tamaño O(r) y se necesita comparar cada tupla en ella con todas sus tuplas. A pesar de que en el peor de los casos r es O(n2), se espera que r sea O(n) ya que en general el número de violaciones de una restricción es pequeña, y por lo tanto la mayoría de los elementos en una categoría se relacionan con un único elemento en una categoría superior.
Luego, para realizar los cambios que restauran la consistencia es necesario obtener el o los elementos que hacen rollup a un elemento inconsistente e ∈ ci, sea ese elemento e0 que pertenece a la categoría cinferior con cinferior ![]() (rollup) ci, tal que (e',e) con e ∈ ci. El número de rutas y el costo de computarlas, en el peor de los casos es O(n|C|), pero en la mayoría de los casos, en que el número de elementos inconsistentes es bajo, es de O(|C|). Por lo tanto, el Algoritmo para obtener una r-reparación con correcto sentido semántico se ejecuta en el peor de los casos en O(ms(r2 + n|C|)) y en el caso esperado en O(n2(ms)).
(rollup) ci, tal que (e',e) con e ∈ ci. El número de rutas y el costo de computarlas, en el peor de los casos es O(n|C|), pero en la mayoría de los casos, en que el número de elementos inconsistentes es bajo, es de O(|C|). Por lo tanto, el Algoritmo para obtener una r-reparación con correcto sentido semántico se ejecuta en el peor de los casos en O(ms(r2 + n|C|)) y en el caso esperado en O(n2(ms)).
CONCLUSIONES
Es posible que en determinados casos se permitan encontrar r-reparaciones con correcto sentido semántico al incorporar grados de prioridad y restricciones seguras en las relaciones rollups, para ello es necesario considerar las siguientes heurísticas: (i) no generar nuevas inconsistencias en el proceso de reparación, (ii) elegir, en lo posible, los cambios donde el rollup tenga menor grado de prioridad, (iii) no modificar rollup en la(s) restriccion(es) segura(s). Sin embargo, es posible que al existir restricciones seguras no se pueda encontrar una r-reparación con correcto sentido semántico.
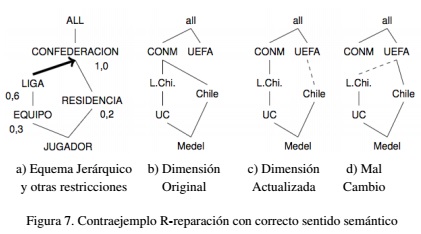
En la Figura 7 se indica un caso donde no es posible computar una r-reparación con correcto sentido semántico, donde la Figura 7(a) se indican las restricciones de prioridad y restricciones seguras del esquema jerárquico mostrado en la Figura 1(a), la dimensión original reflejada en la Figura 7(b) y la actualización a la dimensión indicada en la Figura 5(c). No es posible, bajo las restricciones indicadas en la Figura 7(a) computar la r-reparación reflejada en la Figura 7(d), puesto que cambiar el rollup L.Chi. y CONM por L.Chi. y UEFA viola la restricción segura entre las categorías LIGA y CONFEDERACION.
Como trabajo futuro se tiene la experimentación con grandes volúmenes de datos y comparar el rendimiento con diferentes herramientas para reparar dimensiones inconsistentes.
AGRADECIMIENTOS
Raúl Arredondo y Luis Muñoz agradecen a la Universidad de Los Lagos, a través del proyecto interno de investigación R12/15. Adicionalmente Raúl Arredondo agradece a Mónica Caniupán por insertarlo en el área de investigación en temáticas relevantes en Ciencias de la Computación.
REFERENCIAS BIBLIOGRÁFICAS
Foto Afrati and Phokion Kolaitis. Repair checking in inconsistent databases: algorithms and complexity. In Proceedings of the 12th International Conference on Database Theory, ICDT ’09, pages 31–41. ACM, 2009.
Alexander Anisimov. Review of The data warehouse toolkit: the complete guide to dimensional modeling (2nd edition) by Ralph Kimball, Margy Ross. John Wiley & Sons, Inc. 2002. ACM SIGMOD Record, 32(3):101–102, 2003.
Marcelo Arenas and Leopoldo Bertossi. Answer Sets for Consistent Query Answering in Inconsistent Databases. Theory and Practice of Logic Programming, 3(4):393 – 424, 2003.
Marcelo Arenas, Leopoldo Bertossi, and Jan Chomicki. Consistent query answers in inconsistent databases. In Proceedings of the eighteenth ACM symposium on Principles of database systems PODS’99, pages 68–79. ACM Press, 1999.
Leopoldo Bertossi. Consistent query answering in databases. ACM SIGMOD Record, 35(2):68, June 2006.
Loreto Bravo and Leopoldo Bertossi. Consistent query answering under inclusion dependencies. In Proceedings of the 2004 conference of the Centre for Advanced Studies on Collaborative research, CASCON ’04, pages 202–216. IBM Press, 2004.
Mónica Caniupán and Alejandro Vaisman. Repairing dimension hierarchies under inconsistent reclassification. In ER Workshops, pages 75–85, 2011.
Mónica Caniupán, Loreto Bravo, and Carlos Hurtado. Repairing inconsistent dimensions in data warehouses. Data & Knowledge Engineering, 79-80:17–39, 2012.
Mónica Caniupán, Alejandro Vaisman, and Raúl Arredondo. Efficient repair of dimension hierarchies under inconsistent reclassification. Data & Knowledge Engineering, 95:1–22, 2015.
Surajit Chaudhuri and Umeshwar Dayal. An overview of data warehousing and OLAP technology. ACM SIGMOD Record, 26(1):65–74, 1997. ISSN 0163-5808.
Carlos Hurtado and Claudio Gutierrez. Data Warehouses and OLAP: Concepts, Architectures and Solutions, chapter Handling Structural Heterogeneity in OLAP. Idea Group, Inc, 2007.
Carlos Hurtado, Alberto Mendelzon, and Alejandro Vaisman. Maintaining Data Cubes under Dimension Updates. In Proceedings of the 15th International Conference on Data Engineering, ICDE ’99, pages 346—-. IEEE Computer Society, 1999. ISBN 0-7695-0071-4.
Carlos Hurtado, Claudio Gutierrez, and Alberto Mendelzon. Capturing summarizability with integrity constraints in OLAP. ACM Transactions on Database Systems, 30(3):854–886, 2005.
Ralph Kimball. Slowly changing dimensions. DBMS Magazine, 9(4):14, 1996.
Hans-Joachim Lenz and Arie Shoshani. Summarizability in olap and statistical data bases. In SSDBM, pages 132–143, 1997.
Andrei Lopatenko and Leopoldo Bertossi. Complexity of consistent query answering in databases under cardinalitybased and incremental repair semantics. In Proceedings of the 11th international conference on Database Theory, ICDT’07, pages 179–193. Springer-Verlag, 2006. ISBN 3-540-69269-X, 978-3-540-69269-0.
Recibido: 21/04/2016
Aceptado: 16/02/2017