Mi SciELO
Servicios Personalizados
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Revista Cubana de Ciencias Informáticas
versión On-line ISSN 2227-1899
Rev cuba cienc informat vol.11 no.3 La Habana jul.-set. 2017
ARTÍCULO ORIGINAL
Inferencia de redes de asociación de genes empleando algoritmos genéticos y topología de grafos
Inference of gene association networks using genetic algorithms and graph topology
Liuben López Aparicio1*, Cosme E. Santiesteban-Toca1, Raúl Giráldez Rojo2
1Centro de Bioplantas, Universidad Máximo Gómez Báez, Ciego de Ávila, Carretera a Morón, Km 9½, Cuba, {liuben, cosme}@bioplantas.cu
2Universidad Pablo de Olavide, Sevilla, España, Carretera a Utrera, rgirroj@upo.es
*Autor para la correspondencia: liuben@bioplantas.cu
RESUMEN
Debido a que existe un gran número de enfermedades de naturaleza poligenética, en la actualidad se confiere mayor importancia al resultado de la interacción genética que a la función de cada gen por separado. Por este motivo es muy significativo el estudio de las redes de genes. En los últimos años se ha afrontado el problema de inferir redes de asociación de genes mediante diversas técnicas, sin embargo, a pesar de estos esfuerzos, aun no se logra un grado significativo de precisión al inferir las redes. Es por ello que se propone un algoritmo de inferencia de redes de genes basado en un algoritmo genético que toma en cuenta que muchas de las redes biológicas caracterizadas de forma experimental se ajustan a la topología de grafos libres de escala y de mundo pequeño. Como resultado, este algoritmo logra inferir redes de genes con una alta precisión y manteniendo el sentido biológico.
Palabras clave: Redes de Genes, Algoritmo Genético, Inferencia, Topología de Grafos.
ABSTRACT
Because of the existence of a large number of diseases of polygenic nature, a greater importance to the result of genetic interaction is imparted nowadays to the function of each gene separately. For this reason, it is very significant to study gene networks. In recent years, the problem of inferring gene association networks using various techniques has been tackled, however, despite these efforts, even a significant degree of accuracy is not achieved by inferring networks. That is why an algorithm for inference of gene networks based on a genetic algorithm that takes into account that many of the biological networks characterized so far experimentally, adjust to the free scale and small world graphs topology. As a result, this algorithm achieves to infer gene networks with high accuracy and maintaining the biological sense.
Key words: Gene Networks, Genetic Algorithm, Inference, Graph Topology.
INTRODUCCIÓN
El estudio de enfermedades mono génicas ha alcanzado sus límites, fallando en el tratamiento de enfermedades complejas, en el diseño de fármacos y en el desarrollo de terapias génicas. Motivos que han estimulado el desarrollo de la biología molecular de sistemas donde se observa de forma global los procesos biológicos. Tecnologías como el microarray (Tseng, Ghosh y Feingold 2012), (Breman et al. 2012), (Wang y Li 2011) y (Robinson, McCarthy y Smyth 2010) juegan un papel fundamental en este sentido debido a que mediante estos se puede monitorizar el nivel de expresión de miles de genes simultáneamente, incluso de todo el genoma de un organismo. Por otra parte, el análisis de los microarrays y la extracción de información valiosa de estos, como pudiera ser determinar genes reguladores o una red de coexpresión de genes, es una tarea engorrosa debido al gran volumen de datos que estos contienen.
Las redes de coexpresión de genes o redes de genes se describen matemáticamente como un grafo conexo donde los nodos representan genes y las aristas representan interacciones entre genes, en donde se define que genes presentaran actividad en dependencia de la acción de otros genes.
Muchas de las redes biológicas complejas (Costanzo et al. 2016) caracterizadas de forma experimental hasta la fecha cumplen la propiedad de ser libre de escala y de mundo pequeño. Donde, una red libre de escala es un tipo específico de grafo donde algunos nodos están altamente conectados, es decir, algunos nodos poseen un gran número de enlaces a otros nodos, aunque el grado de conexión de casi todos los nodos es bastante bajo. Y una red de mundo pequeño es un tipo de grafo donde la mayoría de los nodos no son vecinos entre sí, pero la mayoría de los nodos pueden ser alcanzados desde cualquier nodo origen del grafo a través de un número relativamente corto de saltos entre ellos. En el caso de la regulación genética esto es apreciable debido a que se han determinado genes reguladores (o factores de transcripción) que son encargados de desencadenar o inhibir la expresión de varios genes y se logran procesos biológicos complejos con la interacción de un grupo relativamente pequeño de genes.
En los últimos años se han empleado varios algoritmos estocásticos para realizar la inferencia de redes de genes mediante técnicas basadas en similitud, aprendizaje automático, probabilidad y mixtas (Madhamshettiwar et al. 2012), (Zhang et al. 2013), (Maetschke et al. 2014), (Michailidis y D’Alch-Buc 2013), (Kumar, Stecher y Tamura 2016). Sin embargo, a pesar de estos esfuerzos, aun no se logra un grado significativo de precisión al inferir las redes. Es por ello que el objetivo del presente trabajo es desarrollar un algoritmo de inferencia de redes de genes, a partir del empleo de un algoritmo genético de cromosomas variables (Kim y De Weck 2005) y el empleo de la topología de redes, que sea capaz de inferir redes con sentido biológico y que mantenga un alto grado de correlación entre los genes.
Método propuesto ‘‘Algoritmo IRG’’
Los microarrays donde los datos no han sido sometidos a ningún preprocesamiento, se caracterizan por tener muchos rasgos lo que dificulta el procesamiento de los datos. Para reducir la dimensión de estos datos sin perder información útil se realizó un preprocesamiento siguiendo la hipótesis biológica de que: “genes con perfiles de expresión similar comparten el mismo régimen regulatorio” (The GTEx Consortium et al. 2015). Siguiendo esta hipótesis los genes que se expresan de forma irregular en una muestra no serán significativos para las redes a inferir y serán excluidos a partir de un análisis de entropía.
Lectura y preprocesamiento del microarray
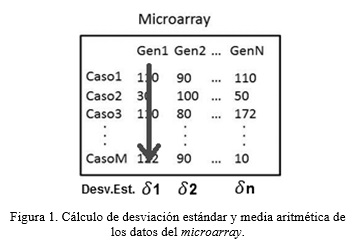
El preprocesamiento de los datos del microarray se realiza haciendo un análisis de la entropía utilizando como base la medida estadística de desviación estándar (Ecuación 1 ) en búsqueda de eliminar los atributos con mayor grado de dispersión. Para este proceso se tomaron un grupo de microarrays y se conformó con estos una matriz numérica de MxN (Figura 1 ) donde cada caso corresponde a los perfiles de expresión genética de un individuo dado y cada rasgo los genes que se están cuantificando. Posteriormente se calcula la desviación estándar para cada rasgo, lo que produce una lista de desviaciones estándar del mismo tamaño que la cantidad de rasgos. Cada valor de esta lista se normaliza de 0 a 1 (Ecuación.2) con vista a eliminar de la matriz aquellos rasgos que tengan un valor de desviación de un 5%, o sea se van a eliminar los que estén por encima de 0.95 y por debajo de 0.05.
En este proceso se obtienen los genes con valores más centralizados y se eliminan los grupos con valores extremos. Con los genes resultantes tras este proceso de selección se construye un nuevo microarray que será sobre el que el algoritmo de inferencia realice la extracción de las redes de genes.

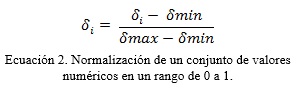
Cálculo del coeficiente de correlación
Tras el preprocesamiento de los datos se calcula la correlación del microarray. Para el cálculo del coeficiente de correlación se utilizó la correlación de Spearman (Ecuación 3 ).
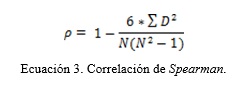
Este método se escogió teniendo en cuenta que no es sensible ante la dispersión y se utiliza para datos donde no se sabe si la distribución es normal (Eisen et al. 1998). Este coeficiente de correlación al igual que otros se encuentra entre los valores de –1 a 1, donde 1 es perfectamente correlacionado, 0 no correlacionado y –1 es perfectamente correlacionado negativamente. En esta investigación se desean los genes que tengan una alta correlación positiva debido a que serán los que tengan un grado de coexpresión más elevado.
Obtención de la matriz de adyacencia
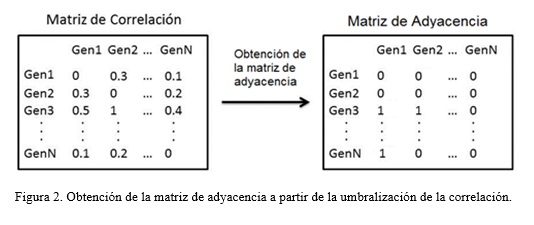
La matriz de adyacencia es una matriz cuadrada que se utiliza como un método de representación de relaciones binarias. Esta matriz establece la relación de todos los genes del microarray a partir de la correlación que existe entre ellos, esto se logra penalizando las correlaciones débiles y maximizando las fuertes (Figura 2). De esta forma, se genera un grafo global que toma como nodos a los genes y como aristas a la relación que existe entre estos. El umbral de selección se estableció en 0.5, donde los genes que tengan una correlación mayor o igual a 0.5 tendrán relación (valor 1 en la matriz de adyacencia), y los que tengan una correlación inferior a 0.5 no tendrán relación (valor 0 la matriz de adyacencia).
Modelo propuesto para la inferencia
La solución que se presenta en este trabajo utiliza como modelo de inferencia un algoritmo genético. Los algoritmos genéticos establecen una analogía entre el conjunto de soluciones de un problema, llamado fenotipo, y el conjunto de individuos de una población natural, codificando la información de cada solución en una cadena, llamada cromosoma. Los símbolos que forman la cadena son llamados los genes. Los cromosomas evolucionan a través de iteraciones, llamadas generaciones. En cada generación, los cromosomas son evaluados usando alguna medida de aptitud o función de fitness. Las siguientes generaciones de cromosomas, llamada descendencia, se forman utilizando los operadores genéticos de cruzamiento y de mutación.
Codificación del vector de entrada
El vector de entrada será de longitud variable o sea son redes de genes de longitudes diferentes. Este vector se descompone en 2 partes: una lista de tuplas, donde cada tupla tienen dos genes y la correlación entre ambos, y la medida de calidad de la red (fitness) (Función 1). En la siguiente figura (Figura 3). Se muestra la estructura de una red de genes. El cálculo y selección de los valores que conforman esta estructura se explica a continuación.
Inicialización de la población
Para generar la población inicial se determina la cantidad de cromosomas que la conformarán y se procede a crear estos cromosomas. Para generar cada cromosoma se irá tomando aleatoria y cíclicamente una cantidad determinada de genes del espacio y se evaluará si son aptos para formar la red. Los genes que formarán un cromosoma son aptos cuando en la menor cantidad de estos estén la mayoría de las aristas o conexiones (grado de conexión), a los que se les denomina como nodos centrales o hubs (Figura 4).
Para esto entre los genes seleccionados se busca el grado de conexión de cada uno con el resto, mediante la matriz de adyacencia y si cumplen con la propiedad descrita anteriormente, se procede a generar las aristas entre ellos. Las aristas se encuentran establecidas en la matriz de adyacencia, de modo que cada gen tendrá conexión con el resto de los seleccionados en base a la matriz de adyacencia. Una característica que debe seguir el grafo generado (cromosoma) es que debe ser conexo, de modo que si fuera seleccionado un gen que no tenga relación con ningún otro del cromosoma se enlaza con el que mayor correlación tenga según la matriz de correlación. Esto generará un grafo que cumple con la propiedad de ser libre de escala donde el peso de las aristas será la correlación que existe entre esos dos nodos según la matriz de correlación.
En este punto cada cromosoma corresponde a un vector de entrada que tendrá una lista de tuplas que describen una arista de un grafo y el peso de esta arista (Figura 3).
Evaluación de la población inicial
La evaluación de la población inicial (cromosomas) se realizará en función de dos parámetros: el ajuste a la topología (libre escala y mundo pequeño), y el grado de correlación media del grafo. Por lo que el valor de fitness de los cromosomas dependerá del ajuste a estos dos parámetros. Para esto se diseñó la siguiente función de fitness:
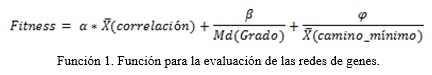
Donde ![]() ,
, ![]() y
y ![]() son constantes ajustables (según la bondad de ajuste calculada
son constantes ajustables (según la bondad de ajuste calculada ![]() = 0.5 ,
= 0.5 , ![]() = 0.25 y
= 0.25 y ![]() =0.25) que sumadas deben dar 1. Esto tiene como objetivo darle un valor de importancia a cada componente de la función y a su vez normalizar los valores de fitness de las redes, debido a que las redes son de tamaño variable y por lo tanto el valor de fitness podría ser afectado por el tamaño del grafo (red de genes).
=0.25) que sumadas deben dar 1. Esto tiene como objetivo darle un valor de importancia a cada componente de la función y a su vez normalizar los valores de fitness de las redes, debido a que las redes son de tamaño variable y por lo tanto el valor de fitness podría ser afectado por el tamaño del grafo (red de genes).
![]() (Correlación) Correlación Media: viene dada por el cálculo de la media de las correlaciones de todas las aristas del grafo. Mientras mayor sea el valor de la
(Correlación) Correlación Media: viene dada por el cálculo de la media de las correlaciones de todas las aristas del grafo. Mientras mayor sea el valor de la ![]() (Correlación) , mayor será el valor de fitness del cromosoma que se está evaluando. Esta medida es la que más peso tiene en la función debido a que la correlación muestra el grado de coexpresión entre los genes y se desean redes con un alto grado de coexpresión entre sus nodos, la correlación de cada par de genes debe tener el mayor valor posible para maximizar la función de evaluación.
(Correlación) , mayor será el valor de fitness del cromosoma que se está evaluando. Esta medida es la que más peso tiene en la función debido a que la correlación muestra el grado de coexpresión entre los genes y se desean redes con un alto grado de coexpresión entre sus nodos, la correlación de cada par de genes debe tener el mayor valor posible para maximizar la función de evaluación.
Md(Grado) Grado de Moda: viene dado por el cálculo de la moda de los grados de todos los nodos del grafo. Debido a que en las redes libres de escala la mayoría de las aristas están en pocos nodos, la mayoría de los nodos tienen pocas aristas y por lo tanto un grado pequeño, por lo cual mientras menor es el grado de moda más se va a maximizar la función de fitness.
![]() (camino_mínimo) Camino Mínimo Medio: viene dado por el cálculo de la media de las distancias de los caminos mínimos de un nodo a todos los nodos de la red. Los caminos mínimos se calculan mediante el algoritmo de Dijkstra (Dijkstra 1959). Debido a que en las redes de mundo pequeño se puede ir de un nodo a otro con pocos saltos, el camino medio debe ser pequeño para que la red cumpla esta propiedad, por lo cual mientras menor es el camino medio de la red más se va a maximizar la función de fitness.
(camino_mínimo) Camino Mínimo Medio: viene dado por el cálculo de la media de las distancias de los caminos mínimos de un nodo a todos los nodos de la red. Los caminos mínimos se calculan mediante el algoritmo de Dijkstra (Dijkstra 1959). Debido a que en las redes de mundo pequeño se puede ir de un nodo a otro con pocos saltos, el camino medio debe ser pequeño para que la red cumpla esta propiedad, por lo cual mientras menor es el camino medio de la red más se va a maximizar la función de fitness.
Los valores resultantes de la evaluación de estas redes a través de la función de fitness se encuentran normalizados en un rango de 0 a 1, siendo más aptas las que posean un valor más elevado. Tras el cálculo del fitness de la población inicial, se almacena su valor según se muestra en la codificación del vector de entrada (Figura 3).
Cruzamiento de los cromosomas
El cruce o recombinación de los cromosomas de la población inicial se realiza tomando pares de cromosomas y cruzándolas por un determinado criterio. El criterio que se implementó es la recombinación en un punto.
Para esto se selecciona el punto medio de dos cromosomas padres y se combinan los fragmentos de forma tal que a partir de dos cromosomas padres se van a generar cuatro hijos (Figura 5).
Tomando en cuenta que estos cromosomas describen un grafo, si tras el proceso de recombinación este queda desconectado se reorganiza el grafo buscando que quede conexo. Esto se realiza examinando en los dos fragmentos de cromosoma padre que conforman el cromosoma hijo los nodos que quedan más cercanos según la matriz de adyacencia y enlazándolos en una nueva tupla que se le agrega al cromosoma hijo. Tras el cruzamiento de los padres los hijos generados se les calculan el valor de fitness y se almacena este valor en el cromosoma (vector de entrada, Figura 3).
Mutación de los cromosomas hijos
La mutación ocurre sobre los hijos en base a una probabilidad estadística por lo general muy baja. Este valor se encuentra entre cero y cien (5 por ciento para este caso). La estrategia de mutación que se implementó consistió en cambiar un nodo central (A) por otro nodo (B) con similar centralidad, posteriormente se estableció una conexión entre los nodos adyacentes al nodo (A) con el nodo (B), basándose en la matriz de adyacencia. Posteriormente se eliminaron del grafo los nodos que estaban enlazados con el nodo (A) y no tienen relación, según la matriz de adyacencia con el nodo (B). Este proceso de mutación va a generar saltos en el espacio de búsqueda lo que evitará que converja rápidamente a óptimos locales. Cuando sucede la mutación se evalúa nuevamente los cromosomas mutados en busca del nuevo valor de fitness, a estos cromosomas.
Selección de la próxima generación
La selección de la próxima generación se implementó mediante el método de la ruleta. Este método consiste en crear una lista con cien posiciones, donde se asignará cada cromosoma una cantidad determinada de veces a la ruleta en función de su valor de fitness. Para esto se unen los cromosomas padres con los hijos en una sola lista, donde cada cromosoma tendrá una probabilidad de ser seleccionado para la nueva generación en dependencia de su valor de fitness. O sea, mientras mayor sea el valor de fitness de un cromosoma más posiciones va a ocupar en la ruleta, por lo que tendrá mayor posibilidad de ser seleccionada, pero como este proceso es pseudoaleatorio pude ser seleccionada una menos apta. De esta lista se va a seleccionar la misma cantidad de cromosomas que había en la población inicial y serán los que la sustituyan, pasando a ser la nueva generación que utilizará el algoritmo para la próxima iteración. Esto tiene como objetivo evitar la convergencia demasiado rápida a una solución local y así reducir el encuentro de falsos descubrimientos.
Condición de parada del algoritmo genético
La condición de parada está dada, primeramente, por el fitness de las redes. Por cada generación se conoce la red que mayor valor de fitness posee e inicialmente se introduce un valor que se va a utilizar como condición de parada o umbral (0.8 para este caso). Cuando una red posea un valor de fitness superior al establecido como umbral el algoritmo genético dejará de crear nuevas generaciones y se devolverán todas las generaciones destacando el mejor cromosoma por cada una de ellas.
En la condición de parada se establece como segunda opción por la cantidad máxima de generaciones. Si suceden una cantidad de generaciones determinada (100 para este caso) y los valores de fitness de los cromosomas generados no alcanzan el valor esperado el proceso debe terminar debido a que estos modelos pueden estar creando nuevas generaciones indefinidamente. Esto es usual para microarrays con una baja correlación de sus genes o por un inadecuado cálculo de la bondad de ajuste del algoritmo para un determinado microarray.
Evaluación experimental
Para la evaluación experimental del algoritmo, se utilizó un grupo de bases de datos del repositorio la Universidad Tecnológica de Nanyang, Singapur. Este repositorio en línea con dirección http://sdmc.lit.org.sg/GEDatasets/Datasets.html, brinda datos biomédicos de alta dimensión, incluyendo los datos de expresión génica. Estas bases de datos fueron seleccionadas debido a que son muy referenciadas y sus datos no han sido sometidos a ningún análisis.
Se utilizaron bases de datos de texto plano de diversa naturaleza, como: Ovarian Cancer (Ovarian), MLL (MLL), ALL-AML Leukemia (Leu 2C), Bcell-Tcell-AML Leukemia (Leu 3C), Bcell-Tcell-BM-PB Leukemia (Leu 4C), Yeast y Central Nervous System (CNS). Las bases de datos pertenecen a perfiles de expresión genética extraídas de un grupo de organismos sanos o enfermos expresados en microarrays.
Análisis de la calidad de las redes obtenidas
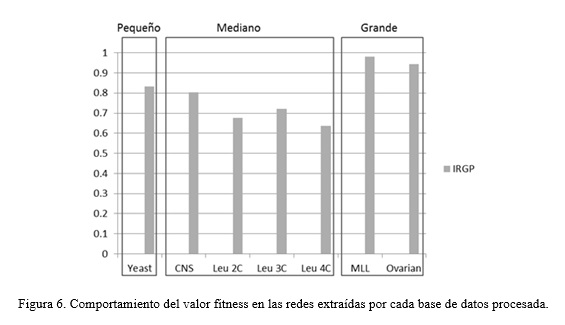
Para el análisis de la experimentación se separaron las bases de datos según las dimensiones de sus datos en: pequeñas (menos de 5000 genes), medianas (de 5000 a 10000 genes) y grandes (más de 10000 genes), esta distribución se mostrará en la figura encerrando cada grupo según su tamaño en un rectángulo (Figura 6).
Teniendo en cuenta que lo que se desea en maximizar el valor de fitness, el algoritmo tuvo un mejor comportamiento en bases de datos de gran dimensión, debido a que en estas fue donde se extrajeron redes con un valor de fitness más elevado. Igualmente se extrajeron redes con un elevado valor de fitness en bases de datos de pequeña dimensión con valores superiores a 0.8. Los resultados más discretos se obtuvieron en bases de datos de mediana dimensión, aunque no fueron críticos con respecto a los resultados obtenidos en bases de datos de pequeña y gran dimensión.
Gráfico de las mejores redes obtenidas
A continuación, se muestran las redes obtenidas por el algoritmo IRG para las bases de datos: Yeast, Central Nervous System (CNS), MLL (MLL) y Ovarian Cancer (Ovarian).
Las redes obtenidas son de diferentes dimensiones y el valor de fitness baría de una a otra. En la aplicación asociada al algoritmo se puede graficar las redes como se muestra a continuación y se obtiene información concreta como: que genes son los que conforman la red, cantidad de nodos y aristas, nodos centrales o posibles factores de transcripción de la red, así como facilidades interactivas de organización y reorganización de la red, y especificaciones de los genes involucrados. Ver Figuras 7, 8, 9, 10
Mecanismo de interpretación
El mecanismo de interpretación del algoritmo viene dado por la codificación del vector que se usa para representar una red o grafo, y por la posibilidad de graficar este vector en una herramienta asociada, lo que permite a los especialistas realizar su experimentación en función de los genes por individual o por grupos (clústeres formados alrededor de un Nodo Central). Si se toma en cuenta que las experimentaciones genéticas por lo general son de forma exhaustiva, en función de un grupo de genes que se sospecha están involucrados en un proceso biológico, el tiempo que puede tardar un investigador en determinar los genes que intervienen en el proceso estudiado es muy extenso. Si a esto se suma que puede ser un grupo de esos genes coexpresándose y que el problema sería combinatorio es casi imposible de hallar una solución en un tiempo razonable.
Usando una de estas redes como modelo a seguir para realizar la experimentación el tiempo se debe reducir considerablemente, debido a que los genes en la vecindad tienen un alto grado de posibilidad de estar involucrados en el mismo proceso, ya que se están expresando de una forma similar cuantitativamente según lo expuesto en la base biológica de la que partimos en la investigación (genes con perfiles de expresión similar comparten el mismo régimen regulatorio).
CONCLUSIONES
Se desarrolló un algoritmo de inferencia de redes de asociación de genes, empleando técnicas evolutivas y genéticas, que es capaz de inferir redes con sentido biológico desde el punto de vista de la topología de grafos empleada y que mantienen un alto grado de correlación entre los genes.
Se propuso una nueva medida de evaluación de las redes de genes, basada en las características topológicas y el nivel de correlación que ésta alcanza, que se ajusta a los principios biológicos de la interacción genética.
AGRADECIMIENTOS
Al Laboratorio de Bioinformática del Centro de Bioplantas, en Ciego de Ávila, Cuba.
REFERENCIAS BIBLIOGRÁFICAS
BREMAN, A., PURSLEY, A.N., HIXSON, P., BI, W., WARD, P., BACINO, C.A., SHAW, C., LUPSKI, J.R., BEAUDET, A., PATEL, A., CHEUNG, S.W. y VAN DEN VEYVER, I., 2012. Prenatal chromosomal microarray analysis in a diagnostic laboratory; experience with >1000 cases and review of the literature. Prenatal Diagnosis, vol. 32, no. 4, pp. 351-361. ISSN 01973851. DOI 10.1002/pd.3861.
COSTANZO, M., VANDERSLUIS, B., KOCH, E.N., BARYSHNIKOVA, A., PONS, C., TAN, G., WANG, W., USAJ, M., HANCHARD, J., LEE, S.D., PELECHANO, V., STYLES, E.B., BILLMANN, M., VAN LEEUWEN, J., VAN DYK, N., LIN, Z.-Y., KUZMIN, E., NELSON, J., PIOTROWSKI, J.S., SRIKUMAR, T., BAHR, S., CHEN, Y., DESHPANDE, R., KURAT, C.F., LI, S.C., LI, Z., USAJ, M.M., OKADA, H., PASCOE, N., SAN LUIS, B.-J., SHARIFPOOR, S., SHUTERIQI, E., SIMPKINS, S.W., SNIDER, J., SURESH, H.G., TAN, Y., ZHU, H., MALOD-DOGNIN, N., JANJIC, V., PRZULJ, N., TROYANSKAYA, O.G., STAGLJAR, I., XIA, T., OHYA, Y., GINGRAS, A.-C., RAUGHT, B., BOUTROS, M., STEINMETZ, L.M., MOORE, C.L., ROSEBROCK, A.P., CAUDY, A.A., MYERS, C.L., ANDREWS, B. y BOONE, C., 2016. A global genetic interaction network maps a wiring diagram of cellular function. Science [en línea], vol. 353, no. 6306, pp. aaf1420-aaf1420. ISSN 0036-8075. DOI 10.1126/science.aaf1420. Disponible en: http://www.sciencemag.org/cgi/doi/10.1126/science.aaf1420.
DIJKSTRA, E.W., 1959. A note on two problems in connexion with graphs. SpringerLink,
EISEN, M., SPELLMAN, P.T., BROWN, P.O. y BOTSTEIN, D., 1998. Cluster analysis and display of genome-wide expression patterns. National Academy of Sciences of the United States of America,
KIM, I.Y. y DE WECK, O.L., 2005. Variable chromosome length genetic algorithm for progressive refinement in topology optimization. Structural and Multidisciplinary Optimization, vol. 29, no. 6, pp. 445-456. ISSN 1615147X. DOI 10.1007/s00158-004-0498-5.
KUMAR, S., STECHER, G. y TAMURA, K., 2016. MEGA7 : Molecular Evolutionary Genetics Analysis Version 7 . 0 for Bigger Datasets Brief communication. MBE, pp. 1-5. DOI 10.1093/molbev/msw054.
MADHAMSHETTIWAR, P.B., MAETSCHKE, S.R., DAVIS, M.J., REVERTER, A. y RAGAN, M.A., 2012. Gene regulatory network inference: evaluation and application to ovarian cancer allows the prioritization of drug targets. Genome Medicine [en línea], vol. 4, no. 5, pp. 41. ISSN 1756-994X. DOI 10.1186/gm340. Disponible en: http://genomemedicine.biomedcentral.com/articles/10.1186/gm340.
MAETSCHKE, S.R., MADHAMSHETTIWAR, P.B., DAVIS, M.J. y RAGAN, M.A., 2014. Supervised, semi-supervised and unsupervised inference of gene regulatory networks. Briefings in Bioinformatics, vol. 15, no. 2, pp. 195-211. ISSN 14774054. DOI 10.1093/bib/bbt034.
MICHAILIDIS, G. y D’ALCH-BUC, F., 2013. Autoregressive models for gene regulatory network inference: Sparsity, stability and causality issues. Mathematical Biosciences [en línea], vol. 246, no. 2, pp. 326-334. ISSN 00255564. DOI 10.1016/j.mbs.2013.10.003. Disponible en: http://dx.doi.org/10.1016/j.mbs.2013.10.003.
ROBINSON, M.D., MCCARTHY, D.J. y SMYTH, G.K., 2010. edgeR: A Bioconductor package for differential expression analysis of digital gene expression data. Bioinformatics, vol. 26, no. 1, pp. 139-140. ISSN 13674803. DOI 10.1093/bioinformatics/btp616.
THE GTEX CONSORTIUM, WELTER, D., MACARTHUR, J., MORALES, J., BURDETT, T., HALL, P., JUNKINS, H., KLEMM, A., FLICEK, P., MANOLIO, T., HINDORFF, L., PARKINSON, H., VISSCHER, P.M., BROWN, M.A., MCCARTHY, M.I., YANG, J., STRANGER, B.E., STAHL, E.A., RAJ, T., WARD, L.D., KELLIS, M., MAURANO, M.T., HUMBERT, R., RYNES, E., THURMAN, R.E., HAUGEN, E. y ET, A., 2015. The Genotype-Tissue Expression (GTEx) pilot analysis: multitissue gene regulation in humans. Science [en línea], vol. 348, no. 6235, pp. 648-60. ISSN 1095-9203. DOI 10.1126/science.1262110. Disponible en: http://www.ncbi.nlm.nih.gov/pubmed/25954001%5Cnhttp://www.pubmedcentral.nih.gov/articlerender.fcgi?artid=PMC4547484.
TSENG, G.C., GHOSH, D. y FEINGOLD, E., 2012. Comprehensive literature review and statistical considerations for microarray meta-analysis. Nucleic Acids Research, vol. 40, no. 9, pp. 3785-3799. ISSN 03051048. DOI 10.1093/nar/gkr1265.
WANG, L. y LI, P.C.H., 2011. Microfluidic DNA microarray analysis: A review. Analytica Chimica Acta [en línea], vol. 687, no. 1, pp. 12-27. ISSN 00032670. DOI 10.1016/j.aca.2010.11.056. Disponible en: http://dx.doi.org/10.1016/j.aca.2010.11.056.
ZHANG, X., LIU, K., LIU, Z.P., DUVAL, B., RICHER, J.M., ZHAO, X.M., HAO, J.K. y CHEN, L., 2013. NARROMI: A noise and redundancy reduction technique improves accuracy of gene regulatory network inference. Bioinformatics, vol. 29, no. 1, pp. 106-113. ISSN 13674803. DOI 10.1093/bioinformatics/bts619.
Recibido: 20/05/2017
Aceptado: 25/06/2017