Meu SciELO
Serviços Personalizados
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares em
SciELO
Similares em
SciELO
Compartilhar
Revista Cubana de Ciencias Informáticas
versão On-line ISSN 2227-1899
Rev cuba cienc informat vol.12 no.1 La Habana jan.-mar. 2018
ARTÍCULO ORIGINAL
Algoritmo meta-heurístico Firefly aplicado al pre-entrenamiento de redes neuronales artificiales
Firefly meta-heuristic algorithm applied to artificial neural network pre-training
Jairo Rojas Delgado1*, Rafael Trujillo Rasúa1
1Facultad de Ciencias y Tecnologías Computacionales. Universidad de las Ciencias Informáticas. La Habana, Cuba.
*Autor para la correspondencia: jrdelgado@uci.cu
RESUMEN
El campo de investigaciones referente a las Redes Neuronales Artificiales (RNA) es uno de los más activos en la comunidad científica con múltiples aplicaciones recientes. El algoritmo Firefly ha sido empleado con éxito en el pre-entrenamiento de RNAs con el objetivo de evitar la convergencia en mínimos locales de métodos de entrenamiento convencionales como el algoritmo Stochastic Gradient Descent (SGD). Sin embargo, en redes con un considerable número de parámetros, el pre-entrenamiento pasa a ser un problema de optimización en espacios de elevada dimensionalidad, y la aplicación del algoritmo Firefly, así como cualquier meta-heurística, presenta limitaciones computacionales a considerar. En este trabajo se investiga una variante del algoritmo Firefly que permite entrenar una RNA con un subconjunto del conjunto de patrones de entrenamiento original sin disminuir la precisión.
Palabras clave: aprendizaje profundo, firefly, mínimo local, pre-entrenamiento, redes neuronales artificiales.
ABSTRACT
Artificial Neural Networks (ANN) is an active research topic in the scientific community. Firefly algorithm has been successfully used on pre-training ANNs, aiming to avoid local minima convergence of conventional training methods such as Stochastic Gradient Descent. However, pre-training ANNs with a high number of parameters using Firefly algorithms, or any other metaheuristic optimization technique, usually is a high computationally complex task. This paper presents a variation of the firefly algorithm that trains the ANN with a subset of training patterns without causing negative effects in the convergence.
Key words: artificial neural network, deep learning, firefly, local minima, pre-training.
INTRODUCCIÓN
El campo de investigaciones referente a las Redes Neuronales Artificiales (RNA) es uno de los más activos en la comunidad científica con aplicaciones recientes en áreas como el reconocimiento de imágenes (Simonyan and Zisserman, 2014; Ciresan et al., 2012), el procesamiento de señales (Yu and Deng, 2011) y la síntesis de voz (Dahl et al., 2012; Hannun et al., 2014). El entrenamiento de una RNA se realiza a través de la minimización de una superficie de error generada a partir de la presentación de patrones de entrenamiento, usualmente mediante el procedimiento conocido como Stochastic Gradient Descent (SGD), o variaciones de este, que se caracteriza por su poca capacidad para evadir mínimos locales.
El surgimiento relativamente reciente del Aprendizaje Profundo (Deep Learning) propone RNAs con un mayor número de capas, un mayor número de neuronas, y consecuentemente un considerable número de parámetros, en el orden de 106 (Yu and Deng, 2011). Se ha mostrado que las superficies de error surgidas durante el entrenamiento de RNAs de este tipo son no convexas (Janzamin et al., 2015) y la cantidad de mínimos locales se incrementa exponencialmente en la medida que aumenta la cantidad de parámetros o el tamaño de la red (Ge et al., 2015; Lipton, 2016). Esto causa una disminución de la convergencia de los métodos de entrenamiento tipo gradiente descendiente hacia mínimos globales, y por tanto de la precisión del entrenamiento.
Los métodos de optimización estocásticos, como los algoritmos evolutivos y metaheurísticas bioinspiradas, han sido empleados de manera combinada con el SGD para el entrenamiento de RNAs convencionales, con el objetivo de evitar la convergencia en mínimos locales (Mavrovouniotis and Yang, 2013; Sahel and Boudour, 2015). La idea básica es encontrar un punto en el espacio de parámetros de la red ubicado en la pendiente donde se ubica al mínimo global, y posteriormente refinar la solución mediante el algoritmo SGD.
El problema de entrenamiento de una RNA se formula como un problema de optimización. Formalmente, dada una función f(w,X) que mide el error de la red al evaluar un conjunto de patrones de entrenamiento X, donde w ![]() es el vector de pesos o parámetros de una RNA, el problema de optimización se define como:
es el vector de pesos o parámetros de una RNA, el problema de optimización se define como:
![]()
donde
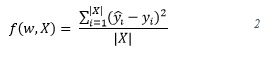
siendo ![]() la salida esperada y la salida real de la red respectivamente para el patrón xi del conjunto X. La definición de la función objetivo se conoce también como el error cuadrático medio (MSE, Mean Squared Error).
la salida esperada y la salida real de la red respectivamente para el patrón xi del conjunto X. La definición de la función objetivo se conoce también como el error cuadrático medio (MSE, Mean Squared Error).
Se ha demostrado que la optimización de los pesos de una RNA es un problema NP-hard (Lipton, 2016). Uno de los problemas más complejos se relaciona con el costo computacional de evaluar la función objetivo , pues se debe evaluar la RNA para cada uno de los elementos del conjunto X.
En la Figura 1 se muestra el efecto del incremento de la cantidad de parámetros w y la cardinalidad del conjunto de patrones de entrenamiento X en la precisión de los modelos de RNAs. Se puede observar que no es suficiente incrementar la cantidad de parámetros, sino también es necesario aumentar la cantidad de patrones de entrenamiento para obtener modelos más precisos. La explicación de esta relación tiene sus orígenes en el principio de parsimonia u overfitting (Hawkins, 2004) como se le denomina por lo regular en la bibliografía especializada.
El empleo de métodos heurísticos de optimización global aplicados al problema de pre-entrenamiento de RNAs se encuentra actualmente limitado por la expansión del espacio de búsqueda definido por w y por el costo de evaluar la función objetivo f(w,X). En este trabajo se estudia el efecto de disminuir la cantidad de patrones de entrenamiento para dirigir la búsqueda realizada mediante el algoritmo Firefly (Yang and Press, 2010), el cual ha sido empleado anteriormente en problemas de elevada dimensionalidad (Nandy et al., 2012; Nayak et al., 2015). Nuestra hipótesis es que si se emplea el algoritmo Firefly para resolver el problema (1) en el proceso de entrenamiento, es posible disminuir la cantidad de patrones en X empleados y a la vez obtener precisiones similares.
El presente documento se encuentra estructurado de la siguiente forma: una primera sección dedicada al estudio del problema de optimización que surge durante el entrenamiento de RNAs, el problema de los mínimos locales y el algoritmo meta-heurístico Firefly, seguida de una segunda sección donde se abordan temas referidos a la configuración de los parámetros del algoritmo Firefly. Finalmente se analizan los resultados experimentales obtenidos y se muestran las conclusiones del trabajo.
Entrenamiento de redes neuronales artificiales
Introducción a las redes neuronales artificiales
Las RNAs, también conocidas como modelos conexionistas surgieron en 1943 introducidas por McCulloch y Pitts en el trabajo titulado Perceptrons. Una perspectiva común para su caracterización es la idea del Procesamiento Paralelo Distribuido (McClelland et al., 1987). Bajo esta perspectiva las RNAs son variaciones de un modelo de procesamiento paralelo distribuido que se caracteriza por un grupo de aspectos de los cuales a continuación se enumeran los más importantes para nuestro análisis.
1. Unidades de procesamiento (Neuronas). Cada unidad de procesamiento realiza un trabajo relativamente simple: recibir una entrada de sus unidades vecinas o de fuentes externas y usar esta entrada para producir una señal de salida que se propaga luego hacia otras unidades de procesamiento o hacia la salida de la red. En esta investigación se emplea un tipo de unidades de procesamiento conocidas en la bibliografía como sigma-units cuya regla de propagación corresponde a la Ecuación 3.
En la Ecuación 3 Wjk es el peso asociado a la entrada ![]() es el bias correspondiente a la neurona k n un instante de tiempo t. Posteriormente el valor sk se evalúa en una función de activación para acotar la contribución de la entrada neta en la activación de la neurona. Frecuentemente se emplea una función no decreciente como la que se muestra en la Ecuación 4.
es el bias correspondiente a la neurona k n un instante de tiempo t. Posteriormente el valor sk se evalúa en una función de activación para acotar la contribución de la entrada neta en la activación de la neurona. Frecuentemente se emplea una función no decreciente como la que se muestra en la Ecuación 4.
![]()
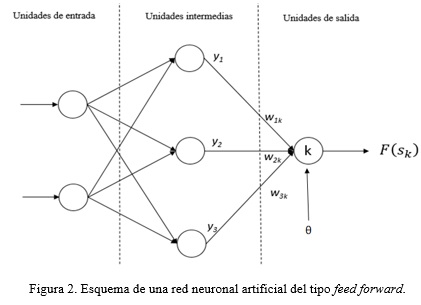
2. Patrón de conectividad entre unidades de procesamiento. Las unidades de procesamiento se encuentran conectadas unas con otras. La forma en que se establecen estas conexiones determina lo que la red es capaz de representar y aprender. Entre las arquitecturas de conexión más frecuentes se encuentran las redes feed-forward, recurrent y convolutional.
Las redes feed-forward son las más simples y empleadas (Figura 2). Esta arquitectura se basa en un grupo de capas de unidades organizadas en cascada. Las unidades ubicadas en una misma capa no poseen conexiones entre ellas, reciben su entrada de la salida de las unidades ubicadas en la capa anterior, y envían sus salidas a las unidades en la capa posterior. Por simplicidad en lo subsiguiente se asumirá que una RNA del tipo feed-forward se encuentra conformada por una capa de neuronas de entrada, la cual no realiza procesamiento, una capa de neuronas intermedias u ocultas y una capa de neuronas de salida. Esta configuración particular es ampliamente reconocida como una red del tipo multilayer perceptron.
3. Regla de aprendizaje. Para que una red reconozca determinado problema es necesario un procedimiento que modifique los patrones de conectividad a partir de la experiencia obtenida de los patrones de entrenamiento. Esto significa entrenar la red o, lo que es lo mismo, modificar los pesos que ponderan la importancia de las entradas de cada neurona.
Para el entrenamiento de RNAs tradicionalmente se emplea el algoritmo SGD. Este algoritmo realiza un recorrido en el espacio de parámetros de una red de forma tal que se minimice la función de error f(w, X),
siguiendo iterativamente la dirección de un gradiente de error calculado en un punto inicial aleatorio del espacio de parámetros. En cada paso se realizan pequeños movimientos en la dirección contraria de dicho gradiente hasta que encuentra un mínimo. Debido a este comportamiento, la familia de algoritmos basados en gradiente descendente es sensible a converger en mínimos locales del espacio de parámetros, y por tanto es sensible a los valores iniciales de los pesos de la red.
Optimizadores globales para el problema de los mínimos locales
Investigadores del campo de Deep Learning coinciden en que los modelos construidos convergen en mínimos locales (Lipton, 2016). El problema se agudiza al considerar que bajo ciertas condiciones, la gran mayoría de irregularidades en las superficies de error no son mínimos locales sino puntos de montura (saddle points) que se comportan como un mínimo y un máximo local simultáneamente (Lipton, 2016). La dificultad fundamental es que dichos puntos de montura se encuentran rodeados por elevadas plataformas de error que pueden disminuir considerablemente la velocidad de convergencia de los algoritmos de aprendizaje (Janzamin et al., 2015).
Los métodos estocásticos de búsqueda se caracterizan por ser optimizadores globales (Khan and Sahai, 2012; Mavrovouniotis and Yang, 2013; Raja and Rajagopalan, 2014). El objetivo de estas soluciones es emplear algoritmos meta-heurísticos con dos rasgos fundamentales: explotación local y exploración global. Existen reportes experimentales de resultados para meta-heurísticas como Cuckoo Search (Valian et al., 2011; Nawi et al., 2015a; Sreeshakthy and Preethi, 2016), Firefly (Nandy et al., 2012; Nayak et al., 2015), Wolf Search (Nawi et al., 2015b), colonia de hormigas (Mavrovouniotis and Yang, 2013; Pandian, 2013), enjambre de partículas (Gudise and Venayagamoorthy, 2003) y enfoques híbridos (Chen et al., 2015).
Entrenamiento basado en el algoritmo metaheurístico Firefly
El algoritmo Firefly fue desarrollado por Xin-She Yang en el año 2007, inspirado en el apareamiento de las luciérnagas mediante destellos de luz (bioluminiscencia) De acuerdo a (Yang, 2012) el algoritmo Firefly se basa en tres principios idealizados: todas las luciérnagas son del mismo sexo; la atracción entre dos luciérnagas es proporcional a su brillo y a la distancia entre ellas, de forma tal que la de menor brillo se moverá hacia la de mayor brillo; y el brillo de una luciérnaga se encuentra determinado por la función objetivo.
En el Algoritmo 1 se indican los pasos fundamentales del algoritmo Firefly. En el paso 1 del algoritmo se genera aleatoriamente la población inicial de luciérnagas. La generación aleatoria de la población de luciérnagas determina la capacidad de exploración global del algoritmo. En nuestro problema, cada luciérnaga representa un vector de pesos , por lo que se generan números aleatorios para cada peso ![]() siguiendo una distribución normal.
siguiendo una distribución normal.
En el paso 2 del algoritmo se calcula el brillo de cada individuo a partir de la función objetivo, que para nuestro problema sería la definida en la Ecuación 2. En el paso 3 se establece un grupo de parámetros de configuración del algoritmo. El coeficiente de absorción λ simula el fenómeno de atenuación de la luz entre dos luciérnagas respecto a la distancia entre ellas. La atracción β cuando la distancia entre dos luciérnagas es cero es una especie de ratio de aprendizaje que controla el paso en que una luciérnaga se mueve en dirección a otra más brillante. Finalmente el parámetro de aleatoriedad η controla en qué medida una luciérnaga puede moverse de forma aleatoria, por lo que este parámetro tiene una estrecha relación con la capacidad de exploración del algoritmo.
El paso 4 es el ciclo de ejecución del algoritmo, determinado por un número máximo de iteraciones, aunque bien puede ser condicionado mediante alguna medida de precisión de la solución dada una tolerancia de error. Los pasos del 5 al 10 simulan el movimiento de las luciérnagas menos brillantes hacia aquellas de mayor brillo. Esto provoca que cada individuo realice una exploración en el espacio de parámetros con una elevada probabilidad de encontrar la solución global. En el paso 15 el algoritmo devuelve el mejor individuo de la población, que sería la solución encontrada.
Aproximaciones de la función objetivo para reducir la complejidad temporal de su evaluación
Si el espacio de parámetros de una RNA estuviera constituido por solo dos pesos, la superficie de error definida por los patrones de entrenamiento pudiera representarse como un paisaje conformado por valles y colinas. Un individuo en un punto cualquiera de ese paisaje en busca de una elevación tendría que decidir en qué dirección ir. Esto se corresponde al hecho de generar un grupo de soluciones candidatas y, sobre la base de cierta experiencia, elegir cuál podría ser la mejor. En la práctica esa experiencia se encuentra modelada en la función objetivo. La función objetivo de alguna forma representa una medida de la altura o calidad de cada solución candidata.
Planteamos la conjetura de que no es necesario obtener una medición altamente precisa de la función objetivo para comparar cualitativamente soluciones candidatas. Por ejemplo, no siempre es un requisito conocer la cantidad exacta de metros de altura de dos elevaciones para estimar que una es más alta que la otra. De este modo, es posible reducir la cantidad de patrones que se emplean para calcular el valor de la función objetivo sin que esto afecte la capacidad de exploración y explotación del algoritmo Firefly. Para reducir la cantidad de patrones se realiza un muestreo del conjunto de entrenamiento inicial. Este muestreo se realiza aleatoriamente siguiendo una distribución uniforme.
RESULTADOS Y DISCUSIÓN
Selección de bases de datos de prueba y configuración de parámetros
En esta sección se describe un grupo de pruebas realizadas para constatar el efecto de disminuir la cantidad de patrones de entrenamiento en la velocidad de convergencia del algoritmo Firefly aplicado al problema de pre-entrenamiento de RNAs. Las pruebas se realizaron empleando una RNA mutlilayer perceptron con unidades sigmoid. Para medir la calidad de cada individuo se empleó la métrica MSE (Ecuación 2). Para las pruebas se escogieron tres modelos de RNAs obtenidos de las siguientes bases de datos de regresión (Lichman, 2013):
-
Wine Quality Data Set. Se trata de una base de datos relacionada con muestras de vino tinto tomadas en el norte de Portugal. El objetivo es predecir la calidad del vino basado en un grupo de pruebas físico-químicas. La base de datos contiene 4898 instancias y 12 atributos. El modelo de RNA se compone de 11 unidades de entrada, 14 unidades intermedias y 1 unidad de salida para un total de 183 parámetros.
-
Concrete Compressive Strength Data Set. La base de datos está relacionada con la capacidad compresiva del concreto. La fortaleza compresiva del concreto es una función no lineal que involucra el tiempo y los ingredientes empleados. El problema consiste en predecir la fortaleza compresiva de un concreto caracterizado por sus atributos o ingredientes. La base de datos contiene 1030 instancias, para las cuales se consideran 9 atributos. Las pruebas se realizaron empleando una RNA con 8 unidades de entrada, 14 unidades intermedias y 1 unidad de salida para un total de 141 parámetros.
-
Combined Cycle Power Plant Data Set. Esta base de datos contiene información relacionada con el ciclo de producción de energía de una planta durante 6 años. Los atributos consisten en variables ambientales como la presión, la temperatura y la humedad relativa. El objetivo es predecir la cantidad de energía eléctrica que la planta produce cada hora. La base de datos posee 9568 instancias y 5 atributos. Las pruebas se llevaron a cabo con modelos de 4 unidades de entrada, 17 unidades intermedias y 1 unidad de salida para un total de 103 parámetros.
-
El empleo de un subconjunto de patrones para dirigir la búsqueda en el espacio de parámetros de una RNA mediante el algoritmo Firefly ofrece resultados similares en cuanto a precisión, comparado con el empleo de todos los patrones.
-
Desde el punto de vista experimental, emplear un subconjunto de patrones para dirigir la búsqueda en el espacio de parámetros de una RNA posibilita contar con más datos de validación que no son utilizados durante el entrenamiento por lo que es posible reducir el intervalo de confianza para la estimación de errores.
-
Mediante la disminución de la cantidad de patrones de entrenamiento se disminuye la complejidad temporal de la función objetivo que se emplea en la resolución del problema de optimización que surge en el pre-entrenamiento de RNAs, haciendo posible tratar problemas de mayores dimensiones.
Los algoritmos Firefly ySGD se configuraron empleando SMAC (Hutter, 2011), un algoritmo de optimización automática de hiper-parámetros. En base a trabajos previos y recomendaciones en la literatura (Nandy, 2012), se decidió que el tamaño de la población para el algoritmo Firefly sea de 40 individuos.
Medición de la precisión del algoritmo Firefly empleando diferentes cantidades de patrones de entrenamiento
El objetivo de esta prueba es realizar una medición de la precisión del algoritmo Firefly cuando se emplean diferentes cantidades de patrones de entrenamiento en comparación con el algoritmo SGD. Con precisión se refiere al MSE del mejor individuo. La medición del MSE se realiza con todos los patrones de la base de datos, pero el entrenamiento con un subconjunto de este.
En la Figura 3 puede apreciarse el promedio del MSE al emplear distintas cantidades de patrones de entrenamiento para la base de datos 1. En escala de grises, las tonalidades más claras representan una menor cantidad de patrones de entrenamiento comenzando con 50 patrones hasta 1000 patrones con paso 50. En línea azul se presenta el comportamiento del MSE al emplear todos los patrones de entrenamiento. Las mediciones se realizaron con una granularidad de 3 iteraciones en el intervalo de 1 a 500.
La Figura 3 sugiere un incremento en la velocidad de convergencia del algoritmo Firefly al emplear menor cantidad de patrones de entrenamientos. En las primeras iteraciones del algoritmo se aprecia cómo los individuos de la población exploran el espacio de parámetros resultando en oscilaciones pronunciadas del MSE. Posteriormente en las iteraciones siguientes el MSE decae hasta cierto mínimo. Se puede observar que en la medida que la cantidad de patrones se incrementa el algoritmo comienza a converger en una menor cantidad de iteraciones y en mejores soluciones. Sin embargo, al emplear todos los patrones de entrenamiento (ver curva azul) el algoritmo converge más lentamente y en soluciones más pobres.
A continuación, se muestran los resultados de mediciones del MSE promedio para las tres bases de datos estudiadas. Para cada base de datos y para cada cantidad de patrones de entrenamiento se repitieron las mediciones 10 veces, calculando el promedio del MSE promedio en el cual el algoritmo convergió. En la Tabla 1 se presentan los resultados de estas mediciones.
Como puede apreciarse, el empleo de un subconjunto de patrones de la base de datos inicial para dirigir la exploración del espacio de parámetros de una RNA mediante el algoritmo Firefly es factible. Los resultados muestran que el MSE de los subconjuntos de patrones de entrenamiento se comporta de manera similar al MSE cuando todos los patrones de entrenamiento son empleados para el algoritmo Firefly. Sin embargo, este comportamiento no parece mantenerse en el caso del algoritmo SGD, donde la precisión decrece al emplear una menor cantidad de patrones de entrenamiento.
CONCLUSIONES Y RECOMENDACIONES
De forma general, la investigación arrojó las siguientes conclusiones:
REFERENCIAS BIBLIOGRÁFICAS
CHEN Jeng-Fung, DO Quang-Hung, and Ho-Nien Hsieh. Training artificial neural networks by a hybrid pso-cs algorithm. Algorithms, 8(2):292–308, 2015.
CHILIMBI Trishul, SUZUE Yutaka, APACIBLE Johnson, and KALYANARAMAN Karthik. Project adam: Building an efficient and scalable deep learning training system. In 11th USE-NIX Symposium on Operating Systems Design and Implementation (OSDI 14), pages 571–582, 2014.
CIRESAN Dan, MEIER Ueli, and SCHMIDHUBER Jurgen. Multi-column deep neural networks for image classification. In Computer Vision and Pattern Recognition (CVPR), 2012 IEEE Conference on, pages 3642–3649. IEEE, 2012.
DAHL George E, YU Dong, DENG Li, and ACERO Alex. Context-dependent pre-trained deep neural networks for large-vocabulary speech recognition. Audio, Speech, and Language Processing, IEEE Transactions on, 20(1):30–42, 2012.
GE, Rong, et al. Escaping from saddle points—online stochastic gradient for tensor decomposition. En Conference on Learning Theory. 2015. p. 797-842.
GUDISE Venu G and VENAYAGAMOORTHY Ganesh K. Comparison of particle swarm optimization and backpropagation as training algorithms for neural networks. In Swarm Intelligence Symposium, 2003. SIS’03. Proceedings of the 2003 IEEE, pages 110–117. IEEE, 2003.
HANNUN Awni Y, MAAS Andrew L, JURAFSKY Daniel, and ANDREW Y Ng. First-pass large vocabulary continuous speech recognition using bi-directional recurrent dnns. ArXiv preprint arXiv:1408.2873, 2014.
HAWKINS Douglas M. The problem of overfitting. Journal of chemical information and computer sciences, 44(1):1–12, 2004.
HUTTER, Frank; HOOS, Holger H.; LEYTON-BROWN, Kevin. Sequential Model-Based Optimization for General Algorithm Configuration. LION, 2011, vol. 5, p. 507-523.
JANZAMIN Majid, SEDGHI Hanie, and ANANDKUMAR Anima. Beating the perils of non-convexity: Guaranteed training of neural networks using tensor methods. CoRR abs/1506.08473, 2015.
KHAN Koffka and SAHAI Ashok. A comparison of ba, ga, pso, bp and lm for training feed forward neural networks in e-learning context. International Journal of Intelligent Systems and Applications, 4(7):23, 2012.
LICHMAN M. UCI machine http://archive.ics.uci.edu/ml. 2013.
LIPTON Zachary C. Stuck in a what? Adventures in weight space. arXiv preprint arXiv:1602.07320, 2016.
MAVROVOUNIOTIS Michalis and YANG Shengxiang. Evolving neural networks using ant colony optimization with pheromone trail limits. In Computational Intelligence (UKCI), 2013 13th UK Workshop on, pages 16–23. IEEE, 2013.
MCCLELLAND James L, RUMELHART David E, PDP Research Group, et al. Parallel distributed processing, volume 2. MIT press Cambridge, MA, 1987.
NANDY Sudarshan, SARKAR Partha Pratim, and DAS Achintya. Analysis of a nature inspired firefly algorithm based back-propagation neural network training. arXiv preprint arXiv:1206.5360, 2012.
NAWI Nazri Mohd, KHAN Abdullah, and REHMAN MZ. Data classification using metaheuristic cuckoo search technique for levenberg marquardt back propagation (cslm) algorithm. In INTERNATIONAL CONFERENCE ON MATHEMATICS, ENGINEERING AND INDUSTRIAL APPLICATIONS 2014 (ICoMEIA 2014), volume 1660, page 050068. AIP Publishing, 2015a.
NAWI Nazri Mohd, REHMAN MZ, and KHAN Abdullah. Ws-bp: An efficient wolf search based back-propagation algorithm. In INTERNATIONAL CONFERENCE ON MATHEMATICS, ENGINEERING AND INDUSTRIAL APPLICATIONS 2014 (ICoMEIA 2014), volume 1660, page 050027. AIP Publishing, 2015b.
NAYAK Janmenjoy, NAIK Bighnaraj, and BEHERA HS. A novel nature inspired firefly algorithm with higher order neural network: Performance analysis. Engineering Science and Technology, an International Journal, 2015.
PANDIAN Arun. Training neural networks with ant colony optimization. PhD thesis, California State University, Sacramento, 2013.
RAJA V Saishanmuga and RAJAGOPALAN SP. A comparative analysis of optimization techniques for artificial neural network in bio medical applications. Journal of computer science, 10(1):106, 2014.
SIMONYAN Karen and ZISSERMAN Andrew. Very deep convolutional networks for large-scale image recognition. arXiv preprint arXiv:1409.1556, 2014.
SREESHAKTHY M and PREETHI J. Classification of human emotion from deap eeg signal using hybrid improved neural networks with cuckoo search. BRAIN. Broad Research in Artificial Intelligence and Neuroscience, 6(3-4):60–73, 2016.
VALIAN Ehsan, MOHANNA Shahram, and TAVAKOLI Saeed. Improved cuckoo search algorithm for feedforward neural network training. International Journal of Artificial Intelligence & Applications, 2(3):36–43, 2011.
VASSILVITSKII Sergei and ARTHUR David. k-means++: The advantages of careful seeding. In Proceedings of the eighteenth annual ACM-SIAM symposium on Discrete algorithms, pages 1027–1035, 2006.
XU Rui and WUNSCH Don. Clustering, volume 10. John Wiley & Sons, 2008.
YANG Xin-She. Chaos-enhanced firefly algorithm with automatic parameter tuning. Int J Swarm Intell Res, 2(4):125–36, 2012.
YANG Xin-She and PRESS Luniver. Nature-inspired metaheuristic algorithms second edition. 2010.
YU Dong and DENG Li. Deep learning and its applications to signal and information processing [exploratory dsp]. Signal Processing Magazine, IEEE, 28(1):145–154, 2011.
Recibido: 02/10/2017
Aceptado: 29/01/2017