ARTÍCULO ORIGINAL

 

Application of algebraic topology to fingerprint recognitiony

 

Aplicación de la topología algebraica al reconocimiento de impresiones dactilares

 

 

Alejandro Valdés Camejo^1*, Javier Lamar León¹

¹Centro de Aplicaciones de Tecnologías de Avanzada (CENATAV), 7a  21812 e/ 218 y 222, Rpto. Siboney, Playa, C.P. 12200, La Habana, Cuba.

*Autor para la correspondencia: {avaldes,jlamar}@cenatav.co.cu

 

 

---

ABSTRACT

In the present work, an algorithm for fingerprints verification based on an application of the algebraic topology is presented. Specifically,  we propose a representation of impressions  as simplicial complexes and the definition of local structures based  on local filtrations  ordering from the complexes.  This filtrations  are determined by neighboring minutiae. It is also proposed the extraction of a set of features based on the analysis of the homology variation in these filtrations. The features combine information about the quantity and connectivity of papillary ridges in the local structures. In addition, a matching  method based on the extracted topological information is presented. This paper shows that this information is discriminative and can be used in combination with classic geometric features to improve the description of local structures of the impressions and the accuracy in the comparison.

Key words: algebraic topology, homology, fingerprints, topology, verification

---

RESUMEN

En este trabajo se presenta  un algoritmo para la verificación de impresiones dactilares basado en una aplicación de la topología algebraica.  Específicamente,  se propone  una representación de las impresiones como complejos simpliciales y la definición de estructuras locales de las impresiones a partir de filtraciones ordenadas locales de los complejos. Estas filtraciones quedan determinadas por minucias vecinas. También se propone  la extración de un conjunto de rasgos basados en el análisis de la variación de la homología en estas filtraciones. Estos rasgos combinan información acerca de la cantidad y la conectividad de las crestas papilares en las estructuras locales definidas. Además,  se presenta   un método de cotejo de las impresiones  basado en la información topológica extraída. En este trabajo se muestra  que esta información es discriminativa y puede usarse en combinación con rasgos geométricos clásicos para mejorar  la descripción de estructuras  locales de las impresiones y la eficacia en la comparación.

Palabras clave: homología, impresiones dactilares, topología, topología algebraica, verificación

---

 

 

INTRODUCTION

Fingerprint  is one of the most popular and used biometric feature due to its uniqueness and immutability Peralta et al. (2015). Fingerprint verification is the process of deciding if two impressions belong to the same finger or not. A lot of methods have been proposed in the literature for fingerprint verification with excellent results Peralta et al. (2015). However it is not a solved problem. When the fingerprint image quality is poor, the nonlinear distortion is high or the overlap region is too small, the problem become very hard Jain et al. (2010). A constantly objective of researchers is to obtain features that allow more robust matching.

Topology is a mathematical field that studies the properties of the bodies that remain unchanged by continuous transformations. It usually focuses only on features such as shape, size and position; although it is also possible to integrate the objects geometry. Algebraic topology is a branch of topology based on the abstract algebra for the study of topological spaces. Algebraic topology can study structural relationships of spaces that are usually ignored by most common geometric features, for example the space connectivity. These information has been applied in some fields of pattern recognition such as human gait recognition Lamar et al. (2013) with good results. In fingerprint recognition many algorithms uses geometrical  information extracted from local regions of the impression for matching. The topological information can be used to improve the description of local regions where non linear distortions can cause significant changes in the geometry but not in the topology of ridge patterns. Also, it can be used as a new feature when the overlap region is small and few geometrical information is available. The topological information can be combined with classical features to obtain a more accurate matching.

In this work we propose a representation of fingerprints as topological spaces through simplicial complexes. Then, we propose a set of features vectors extracted from the analysis of the homology of locals regions in the simplicial complex. At the end, we propose an algorithm to match two fingerprints based on these vectors and an analysis of its accuracy.

Related  Work

Methods based in minutiae are the most well-known and used for fingerprint recognition Maltoni et al. (2009). Each minutia may be described  by a set of attributes like its position, orientation and type, among others.

Usually, they are consider  as a triplet  m = {x,y, θ}(x,y - minutia location coordinates,  θ - minutia ridge orientation). The minutia based methods  can be grouped into two  families: Global minutiae matching and Local minutiae matching Peralta et al. (2015).

In global matching, usually the fingerprints are represented  as a set of minutiae T = {m1,m2, ..., mn}. Given two  representations T  and T´  the final goal is to perform a match between the sets and give a similarity dependent of the number of minutiae matches. These methods obtain high distinctiveness because they capture fingerprint global spatial relationships Maltoni et al. (2009). On the other hand, generally they have a high computational cost because they need to perform an important alignment process to fit the translation and rotation differences. Examples of algorithms based in global matching are Chen et al. (2013), Liu et al. (2004).

Local matching consists of comparing two fingerprints according to local minutiae structures Maltoni  et al. (2009). These structures are formed by attributes extracted from a minutia neighborhood and the relations- hip with respect to closer minutiae. The structures are invariant to global transformations (translation and rotation). Compared to global matching, the local technique present low computational complexity and high distortion tolerance. It also allow to perform matching with partial information Peralta et al. (2015). However the local matching presents low distinctiveness because they do not take into account the global relationships. Actually, the better results can be obtained by implementing hybrid strategies that perform a local matching to robustly determine pairs of minutiae as alignment candidates followed by a consolidation stage based in global matching Maltoni  et al. (2009). The fingerprint  local matching methods can be classified  in several groups given its local structure representation similarities Maltoni et al. (2009), Peralta et al. (2015). Some of the most important are:

• Nearest Neighbors Jiang and Yau (2000), Chikkerur et al. (2006): This classification involve the firsts and classical works. The local structures are formed by one central minutia and the information about the relationship with respect to some other neighbor minutiae, usually the closests ones. Some of the common features extracted are the distances, angle differences and ridge count between the central minutia and it nearest-neighbor. These information  serves  as  base to the subsequent  works which improve  these structure with other features.

• Fixed Radius Ratha et al. (2000): A fixed distance (d) and a circle of radius d around a central minutia are defined as the neighborhood of the minutia to be analyzed. The main difference with nearest neighbors is that the selection of the minutiae depends on the distance d. The principal problem in these methods are the minutiae mismatch in the region border due to the local distortions. The evolution of these methods is in the direction to avoid this issue.

• Minutiae Triangle Tan and Bhanu (2003), Xu et al. (2007): Triangles are constructed using minutiae as it vertices. Information about the triangles are incorporated such as they angles, side distance,  number of ridge along the sides, triangle type, triangle direction, minutiae density in a local area and others.

• Texture Tico and Kuosmanen (2003), Feng (2008): Information from minutiae is combined with other kind of information relative to the local fingerprint appearance such as ridge local orientation or ridge frequency. Usually sampling points are uniformly distributed around a minutiae and are used to calculate this information.

The algebraic topology has been applied in the pattern recognition and biometric fields Alonso et al. (2015). To the best of our knowledge it has not been applied in fingerprint recognition.

Topology Background

In order to understand the method presented in this work we provide some concepts about algebraic topology. Here we present the mains definitions but it is a large and dense topic. We suggest consulting  more specialized literature such as Edelsbrunner  and Harer (2010) for better understanding.

Definition  1. Zomorodian (2009) A k-simplex (σ) is the convex hull of k + 1 affinely independent pointsbS = {v0,v1, ..., vk}. The points in S are the vertex of the simplex. The dimention of σ is k.

A k-simplex has an intuitive interpretation in Rⁿ. It can be a point, segment, triangle, tetrahedron or other entity of higher dimension. The simplices of different dimension are related by the operator face () (See Def2). For example, the faces of a segment are their points and the faces of a triangle are their sides. A simplicial complex is a set of simplices and their faces where the intersection  between simplices can be only on their faces (See Def 3). A simplicial complex defines a topological space Zomorodian (2009).

Definition  2. Zomorodian (2009) Let σ be a k-simplex defined by S = {v0, v1, ..., vk}. A simplex τ defined by T ⊆ S is a face of σ and has σ as a coface. The relationship is denoted  as τσ and σ >- τ .

Definition  3. Zomorodian (2009) A simplicial complex K is a finite set of simplices such that:

1. If σ ∈ K and τσ ⇒ τ ∈ K.
2. If σ0, σ1 ∈ K ⇒ (τ = σ0 ∩ σ1 = ∨ τ σ0, σ1).

Definition  4. Zomorodian (2009) A filtration ordering of a simplicial complex K is a full ordering of its simplices, such that each prefix of the ordering is a simplicial complex.

Simplicial homology is a topological invariant defined over simplicial complexes. It studies the way in which a k-simplex is connected to a (k − 1)-simplex and how this relationship affects the creation of holes in the k and k − 1 dimensions.

Definition  5. Edelsbrunner and Harer (2010) A d-chain is a formal sum of d-simplices in a simplicial complex. The sum of two d-chains a and b is their symmetric difference a ⊕ b = (a ∪ b) − (a ∩ b).

Definition   6.  Edelsbrunner and Harer (2010) The set of all d-chain in a simplicial complex K and the operation ⊕ form a abelian group and is denoted  as Cd(K).

Definition  7. Edelsbrunner and Harer (2010) Let K be a simplicial complex and σ ∈ K a d-simplex, the boundary ∂d(σ) is the set of all faces of σ in the dimention d − 1. The border of a d-chain is the symmetric difference of its simplices borders.

The operator ∂d sets a relationship between the chain groups of differents dimentions. This relationship allows the definition of the homology groups (See Edelsbrunner  and Harer (2010)). These groups capture important features of the simplicial complexes such as the holes in each dimention.

Persistence homology studies how homology  changes in a simplicial complex through a filtration  ordering. It registers the moment in the filtration  when a hole is created or destroyed for each dimension.  The holes have an intuitive  interpretation in each dimension, for example, in dimension 0 they are convex components, in dimension 1 they are cycles and in dimension 2 they are cavities. As a result of the persistence homology  a list of pairs [a, b) is obtained where a is the index of the d-simplex whose addition creates (born) a hole in the dimension d, and b is the index of the (d + 1)-simplex whose addition causes that this hole disappear (die). If a hole does not disappear, it has a persistence pair [a, ∞) (See Fig 1).

Proposed Method

We present our method split into two subsection: feature extraction and matching. For each subsection we use a set of definitions for a better explanation of our approach.

Feature extraction

The feature extraction stage is divided into four main steps. The first step is the representation of the fingerprint as a topological space through a simplicial complex  (See Def 9). This complex is built from a skeleton image E of the fingerprint. A skeleton image is a binary image that is submitted to a thinning stage which allows for the ridge line thickness to be reduced to one pixel (See Fig 2). The simplicial complex was defined under the assumption that the major information of the fingerprint is determined by the ridge pattern configuration. The objective was to build a simplicial complex  as representative to this pattern as possible.

Definition  8. An edge set C(E) from a skeleton image E, is the set of all edges in the form < (x, y), (u, v) > where (x, y) and (u, v) are the coordinates of neighbor black pixels in E considering the 8-neighborhood of each pixel.

Definition  9. An edge simplicial complex of a skeleton image E, denoted  as S(E) is the set of all elements in C (E) and its faces according  the operator(See Def 2).

The second step is the extraction of the filtrations ordering over the simplicial complex. It is the input of the homology persistence algorithm and is a crucial step because it defines the topological relationships that can be captured. Differing from Lamar et al. (2013), in the fingerprints case, it make no sense to create filtrations over all the complex due to the overlaped region in genuine impressions is not the same. For that reason, in this work we propose to make local filtrations in the simplicial complex. For defining the filtrations it is necessary to define some concepts:

Definition  10. The center  of a simplex σ is the point which coordinates are equal to the mean of the simplex vertex coordinates. The  distance between a simplex and a minutia  d(σ, m) is defined as the Euclidean distance between the simplex center and the minutia. The distance between two simplex d(σi, σj ) is defined  as the Euclidean distance between their centers.

Definition  11. Let S(E) be a simplicial complex defined over a skeleton imagen E and mi a minutia in E; it is defined  as neighborhood of radius r of mi to the set where r > 0.

Definition  12. The filtrations  ordering (mi) and (mi) are the ascending and descending ordering of elements respect to their distances d(σ, mi) where r = d(mi,mj) and mj is the k-th nearest minutia to mi.

Definition  13.  The set Gk(E)  = {(mi),(mi)  | ∀mi∈ M (E),  0 < j ≤ k}is the set of all filtration ordering of the impression E, centered in each minutia mi. The value of k is called neighborhood size.

The filtrations of the definition 12 are an ordering of the simplices in a circular region centered in one minutia. The filtrations g+  describe the ridge flow in the region growing from the center to the borders, and the g− in reverse (See Fig 1). These estructures are rotation and translation invariant. An important consideration of these kind of filtrations is that the size of the filtration  a discriminatory factor.

The third step in the feature extraction stage is the analysis of the homology persistence. For each filtration  in Gk(E) their persistence intervals are calculated (See Def 14). For this objective was used an implementation of the algorithm known as sparse matrix reduction from Edelsbrunner and Harer (2010).

Definition  14. It is defined  as and to the pair lists resulting from homology persistence calculation over the filtrations ordering(mi) y(mi) respectively.

A list of pairs for each dimention in the simplicial complex result from the persistence  calculation of one filtration.  The index p in the term lijprepresents the dimention of the list. In this work we propose to use only dimention 0 because the information in dimention 1 is very poor.

The persistence pairs can be represented in the persistence diagrams  (See Fig 3). The interpretation of these diagrams is related to the connectivity history of the ridge flow through the filtration.  For example, in the case of (See Fig 3), many points appear with finite born time and infinite death time. This is because in this filtration  generally  each ridge appears  as a convex component and continues in this way until the end. Some points with finite death time reflect the time when two ridges are joined and one component dies, for example, in a bifurcation. In the case of many components appear for the first time because the ridges are cut by the circle border and they die when these ridges are joined through the filtration.

The complete set of lijlists of an impression E represent the topological information proposed in this work to extract from E. As a final step, we continue with the idea proposed in Lamar et al. (2013) and define a vector of numbers extracted from the diagrams  (See Def 15).

Definition  15. Let lij be a list of persistence intervals and m the lower value such as m ≥ x and m ≥ y, ∀ [x, y) ∈ lijwith y = ∞, it is denoted  as Vijthe vector of 2*n integer values associated to lij with n ≤ m and is defined ∀ 0 ≤ t < n as:

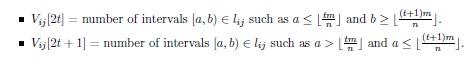
The set of all Vij  is the final features of an impression for the matching process proposed in this work. The information captured by these vectors performs  as a special ridge counter. The number of independent ridges that exists until the filtration  moment appears in the even positions of each vector, and the number of ridges that were born in the filtration  interval appears in the odd positions.

Matching

For each minutia miin one impression E, a set of feature vectors are extracted, which describe a local region determined by mineighbor minutiae (See Def 16). In this work we propose a matching stage based in the comparison of these local regions (See Def 18). The similarity between two impressions is given by their p most similar regions. The best value of p can be estimated in a training stage. This value depend on the fingerprint overlap region and minutiae density.

Definition  16. The topological descriptions from a minutia miis defined as the set bi= {Vij0 , Vij1 ...Vijk} of vectors associated to mi. The set B(E) = {b0,b1...bn}is defined  as the set of all topological descriptions in an impression E.

Definition  17. The similarity  between two topological minutia  descriptions is defined as the function with bi, bj  ∈ B ∧ m = |bi| = |bj | and d is the Euclidean distance.

Definition  18. The similarity  between two  impression I and I´ is defined by where {S0, S1...Sp} are the p-th lowers values of with and the pairs are disjoints.

Global Matching

As was said before the global matching can improve the accuracy in the verification process. In this work we propose a global matching process inspired in Jiang and Yau (2000). The process consist on aligning the sets of minutiae M (I ) and M (I l) of two impression I and I l by the pair of central minutiae of the more similar regions selected in the local matching stage. If mi  is the minutia selected in one impression, the rest of the minutiae are rewritten in the form mj  = {dij , θij , ij } where dij  is the distance between mi  and mj , θij  is the angle differences between their local ridge direction and ij  is the angle between mi  local ridge direction and the line that joins mi  and mj . Then the minutiae set is sorted by the dij  parameter in an ascending way. Finally a simple matching process between the two sets is performed. The final score is where m is the number of minutia matched and

 

EXPERIMENTAL RESULTS

To test our method we use the FVC2002 DB1 database Maio et al. (2002). This database was built with an optical sensor ”TouchView II” by Identix with an image size of 388x374 (142 pixels) and a resolution of 500 dpi. The database contains 8 impression of 110 fingers split into two sets: DB1 (B) with 80 images to train and DB1 (A) with 800 images to test. We follow the same experimental protocol proposed in the competition. In these protocol, the principal measure used to compare the algorithms is the EER (equal error rate) but also are presented the FMR100, FMR1000, ZeroFMR (where FMR mean False Match Rate) Maio et al. (2002).

Our experiments were carried out in two directions. First, we tested our methods using as fingerprint similarity score only the result of the local matching. Secondly we analyze the accuracy of our method by adding the consolidation step based in the global minutia matching. Also, for each test, we changed the features vectors by other features vectors with  some classical  geometric information similar to the ones used by Jiang and Yau (2000) to compare the performance. These geometric feature vectors have the form (dij,θij,ij) where these parameters have the same meaning  as in the global matching (See: Proposed  Method). This geometric information was also added to the topological vectors to analyse the behavior of the combined information.

Table 1 shows the best results obtained in the local matching for each type of features. We performed tests for integer values of parameters p and k in the range 0 < p ≤ 10, 0 < k ≤ 10 where p is the number of descriptions considered for the similarity (See Def 18) and k is the neighborhood  size (See Def 13). Table 2 shows the best results obtained in the global matching (local matching + consolidation step) for each type of features. In this case, we used p = 1 (Because is selected the pair of minutiae descriptions that best match in the local comparison for align) and we consider the values 0 < k ≤ 10.

As shown in Table 1, the local matching based on topological features alone does  not offer good results. This is mainly because the local matching method is based on the selection of the most similar regions. In impostor impressions, is common to find many areas where the ridge pattern is very similar. Generally, these area, were selected by the matching method and these impostors impression received good evaluation results. Nevertheless,  as shown in Table 2, when we added the consolidation step, the EER was reduced from 20 % to 8 %. This is because the global spatial information helps to discriminate between impostors impressions. Also, it means that the selection of the most similar region for alignment in genuine impression, for alignment was correct in the majority of cases. This shows the discriminatory power of these features.

The result of EER = 8,58 % is not one of the  bests reported in the FVC2002 DB1 database. That  means that these topological features by themselves are not enough for a completely verification algorithm. As was said in section Related Works and showed in Table 1 and Table 2, the relationship between the minutiae geometrical features is very discriminative. What we aim to show with our work is that the combination of geometrical features with topological features may provide better results. This can be seen in row 3 of Table 2, where we achieved 2.97 of EER by the combination of both types of features, improving the EER of the geometrical features alone (row 2). This means that the topological information enriched the local region descriptions and allowed a better selection of alignment minutiae.

In the experiments  analysis we find that topological information has better results in impressions where the minutia density is low. It makes sense because in these cases the minutiae neighborhood captures a bigger area and a more complete description of the ridge pattern. Also, in some cases, when the overlap region is small and few minutiae exists, topological features allow a better matching (See Fig 4). The invariance to non linear distortions was not solved completely because the filtration size depend on minutiae neighbors, nevertheless the negative impact in the feature vectors by this concept is small. The main limitation  of topological information is the noise in the ridge connectivity which causes differences in the convex components history.

 

CONCLUSIONS

In this work we presented an algorithm for fingerprint recognition  based on the topological analysis of the ridge pattern through persistence homology. The proposed topological description works like a special ridge counter in the minutiae neighborhood. Experiments showed that this information is discriminative but not enough for an effective matching algorithm by themselves. However the topological information was used to improve the description of fingerprints local structures in combination with other geometrical features. This work is the first application of this topic to fingerprint recognition. In the future we may consider the representation of the fingerprint as a different simplicial complex or the definitions of other filtrations that capture a different information. Also, it is possible to extend this idea to palm print recognition.

 

REFERENCES

R Alonso, E Garc´ıa, and J Lamar. De la homolog´ıa simplicial a la persistencia homol´ogica. un estado del arte. Serie Azul, 2015.

Fanglin Chen, Xiaolin Huang, and Jie Zhou.  Hierarchical minutiae matching for fingerprint and palmprint identification. IEEE Transactions on Image Processing, 22(12):4964–4971, 2013.

S Chikkerur, A N Cartwright,  and V Govindaraju. K-plet and coupled bfs: a graph based fingerprint repre- sentation and matching algorithm.  In International Conference on Biometrics, pages 309–315. Springer,
2006.

H Edelsbrunner and J.L Harer. Computational topology: an introduction. American Mathematical Soc., 2010. J Feng. Combining minutiae descriptors for fingerprint matching. Pattern Recognition, 41(1):342–352, 2008. Anil K Jain, Jianjiang Feng, and Karthik  Nandakumar. Fingerprint matching. Computer, (2):36–44, 2010.

X Jiang and Wei-Yun Yau. Fingerprint minutiae matching based on the local and global structures. In Pattern recognition, 2000. Proceedings. 15th international conference on, volume 2, pages 1038–1041. IEEE, 2000.

Javier Lamar, Edel Garcia-Reyes, Rocio Gonzalez-Diaz, and Raul Alonso-Baryolo. An application for gait recognition using persistent homology. Electronic Journal Image-A, 3 (5), 2013.

Chaoqiang Liu, Tao Xia, and Hui Li.  A hierarchical hough transform  for fingerprint  matching.  Biometric Authentication, pages 171–182, 2004.

D Maio, D Maltoni, R Cappelli, J L Wayman, and A K Jain. Fvc2002: Second fingerprint verification competi- tion. In Pattern recognition, 2002. Proceedings. 16th international conference on, volume 3, pages 811–814. IEEE, 2002.

D Maltoni, D Maio, A Jain, and S Prabhakar. Handbook of fingerprint recognition. Springer Science & Business Media, 2009.

D Peralta, M Galar, I Triguero, D Paternain, S Garc´ıa, E Barrenechea, J M Ben´ıtez, H Bustince, and F Herrera. A survey on fingerprint  minutiae-based local matching for verification and identification: Taxonomy and experimental evaluation. Information Sciences, 315:67–87, 2015.

N K Ratha, R M Bolle, V D Pandit, and V Vaish. Robust fingerprint authentication using local structural similarity.  In Applications of Computer Vision, 2000, Fifth IEEE Workshop on., pages 29–34. IEEE, 2000.

Xuejun Tan and Bir Bhanu. A robust two step approach for fingerprint identification.  Pattern Recognition Letters, 24(13):2127–2134, 2003.

Marius Tico and Pauli Kuosmanen. Fingerprint matching using an orientation-based minutia descriptor. IEEE Transactions on Pattern Analysis and Machine Intelligence, 25(8):1009–1014, 2003.

Wenquan Xu, Xiaoguang Chen, and Jufu Feng. A robust fingerprint matching approach: Growing and fusing of local structures. Advances in Biometrics, pages 134–143, 2007.

A. Zomorodian. Topology for Computing. Cambridge University Press, New York, NY, 2009.

 

 

Recibido: 15/11/2017
Aceptado: 12/10/2018