Mi SciELO
Servicios Personalizados
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Revista Cubana de Ciencias Informáticas
versión On-line ISSN 2227-1899
Rev cuba cienc informat vol.12 no.4 La Habana oct.-dic. 2018
ARTÍCULO ORIGINAL
Selección de variables para el diagnóstico de fallos en chumaceras.
Variables selection for journal bearing fault diagnostic.
Joel Pino Gómez1*, Fidel E. Hernández Montero1, Julio Cesar Gómez Mancilla2
1Universidad Tecnológica de la Habana (CUJAE). 114, Marianao, Habana, Cuba. joelpinogomez@gmail.com, fhernandez@tele.cujae.edu.cu
2Instituto Politécnico Nacional (IPN). Ciudad de México. México. Correo electrónico. gomezmancilla@gmail.com
*Autor para la correspondencia: joelpinogomez@gmail.com
RESUMEN
En la selección de los rasgos más importantes para el diagnóstico de fallos de chumaceras no se considera el conocimiento experto que se expresa en variables no numéricas, sin embargo, esta información puede ser vital para mejorar la eficiencia del diagnóstico. Este trabajo fue desarrollado con el objetivo identificar los rasgos más relevantes para clasificar un grupo de fallos ocurridos en las chumaceras de una turbina de vapor. Los conjuntos de valores de las variables que soportan el trabajo corresponden a los datos almacenados en reportes de diagnóstico y mantenimiento de una termoeléctrica en explotación. Las técnicas aplicadas para procesar los datos cuantitativos y cualitativos son herramientas del enfoque lógico combinatorio al reconocimiento de patrones. Mediante diferentes criterios de comparación se determinó la confusión de los rasgos del conjunto inicial y posteriormente los testores y testores típicos. Finalmente se calculó el peso informacional de los rasgos. Los resultados alcanzados mostraron, entre otras consideraciones, que la relevancia de los rasgos cualitativos que se incorporaron a la descripción de los fallos es superior a la de los rasgos numéricos.
Palabras clave: confusión, mezclados, rasgos, selección, testores
ABSTRACT
Experts in diagnostic can provide essential information, expressed in mixed variables (quantitative and qualitative), about journal bearing faults, nevertheless feature selection researches for fault diagnostic applications forget this important knowhow. This work is focused to identify the most important features for fault identification in a steam turbine journals bearings. The values sets that support this research come from stored diagnostics and maintenance reports of an active thermoelectric power plant. Mixed data processing was accomplished by mean of logical combinatorial pattern recognition tools. Confusion of raw features set was obtained employing different comparison criteria’s. Subsequently was identified the testor and typical testor and compute the informational weight of features that conform typical testor. The values of the mixed features originated by expert knowledge are shown through the obtained results.
Key words: confusion, features, mixed, selecticon, testor
INTRODUCCIÓN
Muchas de las averías en máquinas rotatorias están vinculadas con los fallos de los rodamientos (El-Thalji, 2015; Khelf, 2013; Lei, 2013). Una parte considerable de la industria que centra su funcionamiento en grandes máquinas rotatorias emplea chumaceras. El conocimiento experto sobre los fallos que ocurren en las chumaceras de importantes máquinas rotatorias se expresa en variables de diferente naturaleza, es decir tanto en variables cuantitativas como cualitativas. Seleccionar qué variables se deben utilizar para el diagnóstico dado el conjunto completo de rasgos disponibles, tanto numéricos como no numéricos, es de vital importancia para alcanzar buenos resultados en la clasificación. Hasta ahora los trabajos desarrollados para diagnosticar chumaceras utilizan solo variables cuantitativas que son procesadas utilizando redes neuronales artificiales (ANN), análisis discriminante de Fisher (FDA), máquinas de soporte vectorial (SVM) y K vecinos cercanos (KNN) (Saridakis, 2008; Byungchul, 2014; Babu, 2014; A.Moosavian, 2013), aspecto que limita la efectividad de las técnicas desarrolladas.
El enfoque lógico combinatorio al reconocimiento de patrones aporta herramientas muy útiles para el trabajo con variables mezcladas (rasgos numéricos y no numéricos) que lo hacen idóneo para realizar la selección de los rasgos necesarios para describir los fallos (Ruiz-Shulcloper, 2002). El trabajo que se presenta propone la aplicación de este enfoque a la identificación de los rasgos más importantes que describen fallos en chumaceras de una turbina de vapor. Los conjuntos de valores de las variables que soportan el trabajo corresponden a los datos almacenados en reportes de diagnóstico y mantenimiento de una termoeléctrica en explotación.
Enfoque Lógico Combinatorio
El enfoque lógico combinatorio al reconocimiento de patrones se nutre de la Lógica Matemática, la Teoría de Testores, la Teoría Clásica de Conjuntos, la Teoría de los Subconjuntos Difusos, la Teoría Combinatoria y la Matemática Discreta en general. Esencialmente los objetos son descritos por medio de una combinación de rasgos de diferente naturaleza de manera que todos (incluidos los cualitativos) pueden ser procesados por funciones numéricas (Ruiz-Shulcloper, 2002). El primer problema que atiende este enfoque es la selección de variables, y seguidamente puede atender diferentes tipos de problemas de clasificación (Ruiz-Shulcloper, 2002). El problema que trata este trabajo es de selección de variables, lo cual consiste en encontrar los rasgos que inciden en el problema de manera determinante y reducir el número de rasgos en términos de los cuales se deben describir los objetos. Para desarrollar la selección de variables en este enfoque son muy útiles en primera instancia los criterios de comparación para valores de una variable.
Criterios de Comparación
Un criterio de comparación consiste en una formulación matemática que permite, dados dos valores de un rasgo, calcular un determinado nivel de semejanza o similaridad entre ellos. A continuación se describen brevemente los criterios de comparación (CC) empleados en este trabajo.
El primer criterio de comparación abordado, el criterio de comparación de igualdad (CC1), se empleó con variables no numéricas debido a que el dominio de las variables numéricas utilizadas pertenece al conjunto de los números reales y en tal condición carece de sentido el empleo de este criterio. El CC1 establece que dos valores de un rasgo son semejantes siempre que dichos valores sean iguales o estén vacíos (no se cuenta con información, no existen dichos valores), como se describe en la siguiente expresión (Ruiz-Shulcloper, 2002):

donde Xs(Oi) y Xs(Oj) son los valores del rasgo s para los objetos Oi y Oj, respectivamente.
Otro criterio de comparación empleado en el trabajo, el criterio de pertenencia a un intervalo (CC2), se describe a través de la siguiente expresión:
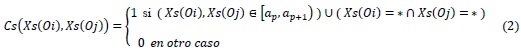
El CC2 establece que si dos valores de un rasgo están dados en un mismo intervalo, entonces son semejantes. Igualmente serán semejantes si ambos objetos presentan ausencia de información para ese rasgo. De lo contrario, son diferentes (Ruiz-Shulcloper, 2002).
La semejanza entre dos datos aritméticos también puede determinarse como una función de las distancias entre ellos, el criterio de cercanía de datos aritméticos (CC3), expresa semejanza en caso de que la diferencia entre dos valores de un rasgo no exceda un umbral, tal como se muestra en la siguiente expresión:
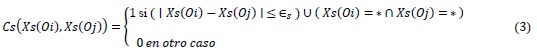
La comparación del rasgo también resultará semejante en caso de que ambos valores estén vacíos (Ruiz-Shulcloper, 2002).
Otro criterio de comparación utilizado en el trabajo es el criterio de cercanía normalizada de datos aritméticos (CC4), el cual también expresa proximidad aritmética entre dos valores de un rasgo. La semejanza de acuerdo a este criterio sedefine de acuerdo a la siguiente ecuación:
![]()
En este caso la diferencia calculada se normaliza a la máxima diferencia admisible (∆Xs) y la sustracción a 1 se realiza para expresar similaridad. A diferencia de los CC2 y CC3, donde la salida es booleana, la salida de CC4 es real. Un resultado cercano a 1 expresa un alto grado de semejanza, mientras que uno próximo a 0 expresa lo contrario (Ruiz- Shulcloper, 2002).
Un criterio que puede utilizarse tanto en variables cuantitativas como cualitativas es el criterio de pertenencia a un conjunto (CC2c), pero al igual que CC1, en este trabajo solo fue empleado para comparar rasgos no numéricos. El criterio CC2c se define como:
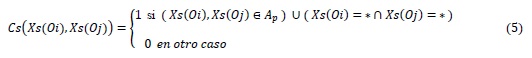
y establece la semejanza entre dos valores si ambos pertenecen a un mismo conjunto (o a la unión finita de varios conjuntos) de valores posibles para el rasgo que se analiza (Ruiz-Shulcloper, 2002).
Confusión.
La confusión (error) introducida por un rasgo (o grupo de rasgos) se define como la cantidad de pares semejantes, de acuerdo a algún criterio de comparación, de valores de un rasgo (o grupo de rasgos) que pertenecen a objetos que yacen en clases distintas. Mientras menor sea la confusión más útil será para diferenciar las clases involucradas en un proceso de clasificación (Ruiz-Shulcloper, 2002).
Testores y Testores típicos. Concepto extendido.
Dado un conjunto de columnas ![]() de una tabla T formada por descripciones de objetos pertenecientes a las clases T0 y T1, si después de eliminar de T todas las columnas, excepto las de
de una tabla T formada por descripciones de objetos pertenecientes a las clases T0 y T1, si después de eliminar de T todas las columnas, excepto las de ![]() , no existe fila alguna en T0 semejante (de acuerdo a algún criterio de comparación) con alguna fila de T1, entonces
, no existe fila alguna en T0 semejante (de acuerdo a algún criterio de comparación) con alguna fila de T1, entonces ![]() se denomina testor de la tabla T para las dos clases T0 y T1. Un testor se llama típico (irreducible) si al eliminar cualquiera de sus columnas este deja de ser un testor para las dos clases T0 y T1 (Ruiz-Shulcloper, 2002). Si en la tabla T existen objetos semejantes, pertenecientes a clases diferentes, entonces no se podrán obtener testores, según la definición planteada.
se denomina testor de la tabla T para las dos clases T0 y T1. Un testor se llama típico (irreducible) si al eliminar cualquiera de sus columnas este deja de ser un testor para las dos clases T0 y T1 (Ruiz-Shulcloper, 2002). Si en la tabla T existen objetos semejantes, pertenecientes a clases diferentes, entonces no se podrán obtener testores, según la definición planteada.
Es difícil encontrar descripciones originales de las clases en matrices sin solapamiento (clases disjuntas), es decir que ningún objeto de una clase sea semejante a algún otro ubicado en otra clase. La definición extendida de testor plantea entonces que, dado un conjunto de columnas ![]() de una tabla T, que puede tener o no objetos semejantes, si después de eliminar de T todas las columnas, excepto las de
de una tabla T, que puede tener o no objetos semejantes, si después de eliminar de T todas las columnas, excepto las de ![]() , no aparecen nuevas sub-descripciones semejantes en clases diferentes, entonces
, no aparecen nuevas sub-descripciones semejantes en clases diferentes, entonces![]() se denomina testor de la tabla T (Ruiz-Shulcloper, 2002).
se denomina testor de la tabla T (Ruiz-Shulcloper, 2002).
Medidas de importancia informacional de los rasgos.
Los testores ofrecen una clara visión de que existen rasgos que aportan mayor información que otros en la clasificación de los objetos. A continuación se describen las medidas de relevancia de un rasgo utilizadas en este trabajo. La relevancia de un rasgo puede determinarse a partir de la cantidad de testores típicos de los que forma parte, así se puede definir la relevancia frecuentista de un rasgo de acuerdo a la siguiente expresión (Ruiz-Shulcloper, 2002):

donde ![]() es el número total de testores típicos y
es el número total de testores típicos y ![]() (x) es el número de testores típicos donde aparece el rasgo x. Según esta medida, un rasgo es más importante en la medida que aparece en una mayor cantidad de testores típicos. Como una medida de importancia complementaria aparece la relevancia longitudinal de un rasgo:
(x) es el número de testores típicos donde aparece el rasgo x. Según esta medida, un rasgo es más importante en la medida que aparece en una mayor cantidad de testores típicos. Como una medida de importancia complementaria aparece la relevancia longitudinal de un rasgo:
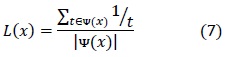
donde t representa la longitud de cada testor típico donde aparece el rasgo x y ![]() (x) representa la cantidad de testores típicos que lo contienen.
(x) representa la cantidad de testores típicos que lo contienen.
Finalmente se expresa la relevancia de un rasgo a partir de una función que considera las medidas anteriores (Ruiz- Shulcloper, 2002).
![]()
donde los parámetros α y β son parámetros de ponderación de la influencia en la relevancia de los factores p(x) y L(x), respectivamente.
MATERIALES Y MÉTODOS
El trabajo se realizó sobre un conjunto de datos proporcionados por especialistas de diagnóstico de una termoeléctrica a partir de las mediciones de las vibraciones de una chumacera durante tres condiciones de fallo diferentes: roturas de babbitt inferior (BI), holguras excesivas (H) y roturas de babbitt inferior y holguras excesivas simultáneamente (BIH).
El trabajo se desarrolló sobre los conjuntos de datos formados por las mediciones de las vibraciones en las direcciones horizontal y vertical. Estos conjuntos se trabajaron de manera independiente debido a que los especialistas de diagnóstico sugieren que los fallos se manifiestan de forma diferente en una y otra dirección de medición, llegando incluso en algunos casos a considerarse irrelevante la información que aporta alguna de las direcciones. Cada conjunto está formado por 215 objetos pertenecientes a la clase BI, 354 objetos pertenecientes a la clase H y 553 objetos pertenecientes a la clase BIH.
Los rasgos utilizados para describir cada uno de los objetos se determinaron a partir de la opinión de los expertos de diagnóstico sobre los registros de vibraciones. Por un lado, de los espectros de amplitud de las vibraciones se obtuvieron 18 variables de naturaleza numérica: 8 variables son los valores de amplitud de los armónicos (1X a 8X), 7 variables son los valores de amplitud de los inter-armónicos presentes, y 3 variables corresponden a frecuencias sub-síncronas. Por otro lado, se obtuvieron 18 variables de naturaleza cualitativa: 1 variable identifica el nombre de la componente predominante en el espectro sin considerar la síncrona (Pred) y 17 variables contienen la relación de las amplitudes de los rasgos espectrales respecto a la amplitud de la componente síncrona (O2 a O18). “Pred” es una variable nominal y los 17 rasgos restantes son ordinales.
A través del cálculo de la confusión entre las clases fue verificada la efectividad de la aplicación de diferentes criterios de comparación y se logró la reducción del conjunto inicial de rasgos. No solo se realizó el cálculo de la confusión entre las clases, es decir, entre BI y H, entre H y BIH, y entre BI y BIH, sino que además se determinó la confusión entre los objetos de una misma clase, es decir, la confusión de BI, la confusión de H y la confusión de BIH.
La confusión de un rasgo (o grupo de rasgos) entre clases se determinó a través de la definición aportada en la Sección 2.2. La confusión de un rasgo (o grupo de rasgos) para una misma clase se determinó en este trabajo como la cantidad de ocasiones en que los valores de un rasgo (o grupo de rasgos) fueron encontrados no semejantes. La semejanza se determina de acuerdo a un determinado criterio de comparación.
El procedimiento de reducción del conjunto de rasgos, así como de selección del criterio de comparación a utilizar para cada rasgo, se basó en la determinación de aquellos rasgos con los que no se sobrepasó un 35% de confusión, tanto para la confusión entre las clases, como para las confusiones propias de cada clase. Cuando varios criterios de comparación no sobrepasan el 35% de confusión para el mismo rasgo, se selecciona el criterio de comparación que arroja menor porciento de confusión.
El cálculo de la confusión siguiendo la metodología antes descrita se llevó a cabo empleando los criterios de comparación CC2, CC3 y CC4, para el conjunto de rasgos numéricos, y los criterios de comparación CC1, CC2, CC3, CC4 y CC2c, para el conjunto de rasgos mezclados. Además, para el conjunto de rasgos mezclados se aplicó el criterio de comparación definido a continuación:
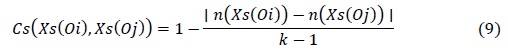
donde n(Xs(Oi)) y n(Xs(Oj)) se refiere a las posiciones de los valores que toma el rasgo s en las descripciones de los objetos i y j, respectivamente, y es el tamaño del alfabeto de posibles valores para el rasgo s.
Este criterio fue nombrado “criterio de cercanía normalizada de datos ordinales” (CCm1), y a través de él es posible analizar la cercanía de dos datos cualitativos ordinales, dado el conjunto finito y completamente ordenado de los valores que puede tomar el rasgo que se analiza.
Con los resultados obtenidos del análisis de la confusión se desarrolló el cálculo de los testores y posteriormente se determinó la importancia informacional de los rasgos presentes en los testores típicos, aplicando las definiciones dadas en los epígrafes 2.3 y 2.4, respectivamente.
RESULTADOS Y DISCUSIÓN
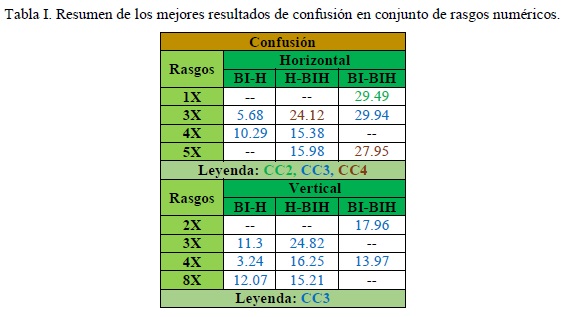
Los resultados de todo el trabajo realizado se exponen a continuación, comenzando por el cálculo de la confusión. En las tabla I y tabla II se muestran los mejores resultados de los cálculos de confusión para el conjunto de datos numéricos y el conjunto de datos mezclados, respectivamente. En ambas tablas aparecen 3 columnas, una para cada par de clases posibles, mientras que cada fila representa uno de los rasgos sobrevivientes del procedimiento de reducción de rasgos. Con diferente color se identifica el criterio de comparación con el que se obtuvo el mejor resultado. En la tabla I se muestra el resumen de los mejores resultados del cálculo de la confusión de los 18 rasgos numéricos. De un total de 18 rasgos presentes en la descripción inicial de cada objeto las variables se redujeron a solo 4 rasgos, para un 22.2% del total de rasgos, tanto para el conjunto de datos de las vibraciones de la dirección horizontal, como de la dirección vertical. De los 3 criterios de comparación empleados, el más efectivo es el CC3 ya que a través de este criterio se obtienen los más bajos porcientos de confusión de modo general.
En la tabla II se aporta el resumen de los mejores resultados de confusión en el caso del conjunto de rasgos mezclados. Como se aprecia, de las 36 variables quedaron 11 (30.5%) para el conjunto de datos correspondiente a las vibraciones de la dirección horizontal y 8 variables (22.2%) quedaron para el conjunto de datos correspondiente a las vibraciones de la dirección vertical. Los porcientos de confusión logrados con el conjunto de rasgos numéricos de las vibraciones de la dirección horizontal (ver tabla I) fueron significativamente mejorados por los alcanzados trabajando con el conjunto de datos mezclados. En este caso, además, los mejores resultados de confusión se alcanzan con el CC2c, superando los resultados alcanzados con CC3, cuando solo se trabajó con los datos numéricos. En este caso también se obtienen menores porcientos de confusión para diferenciar la clase BIH de las clases BI y H. Los resultados mostrados por el conjunto de datos mezclados de la vibración de la dirección vertical reflejan que para diferenciar las clases H y BIH los porcientos de confusión obtenidos son mejores en relación con los logrados para el caso del trabajo con solamente datos numéricos.
En la tabla III aparecen los criterios de comparación seleccionados para cada rasgo.
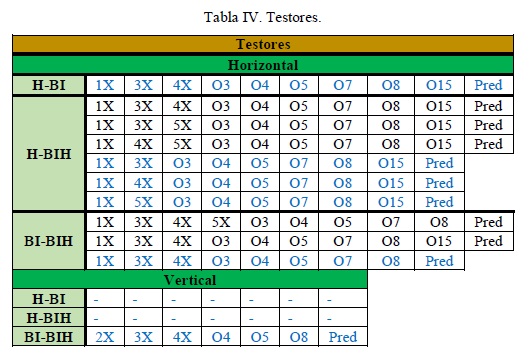
En la tabla IV se muestran los testores (color negro y azul) y testores típicos (color azul) que se obtuvieron para diferenciar las clases correspondientes, tanto para el conjunto de datos de vibraciones de la dirección horizontal como para las vibraciones de la dirección vertical. Se aprecia que las variables cualitativas que se consideran dentro del conjunto de datos mezclados tienen una participación decisiva en la diferenciación de cada una de estas clases. También se evidencia un orden en el que la diferenciación de los pares de los fallos pudiera conducir a mejores resultados atendiendo a la cantidad de testores típicos que existen para cada par; ese orden es H-BIH (con tres testores típicos), BI-BIH (con dos testores típicos) y H-BI (con un testor típico). Además, se demuestra que los resultados para el conjunto de datos de vibraciones de la dirección vertical son pobres, aportando solo un testor. Por último, como el rasgo 8X no aparece en el único testor para el conjunto de datos de vibraciones de la dirección vertical, este puede eliminarse.
El cálculo del peso informacional de cada uno de los rasgos que conforman los testores típicos se calculó de acuerdo con la ecuación (8), obteniéndose los resultados que se muestran en la tabla V.
No se expone la relevancia de los rasgos que conforman el único testor típico para las vibraciones de la dirección vertical debido a que carece de sentido hacerlo, pues todos tienen la misma relevancia (solo se obtuvo un testor). Los rasgos más importantes para la diferenciación de las clases, de acuerdo con los resultados mostrados en la tabla V, son, en primer lugar, los rasgos 1X, O3, O4, O5, O7, O8 y Pred, en segundo lugar, los rasgos O15, 3X y 4X, y por último, el rasgo 5X.
CONCLUSIONES
Este trabajo constituye la aplicación de un enfoque de reconocimiento de patrones a la identificación de los rasgos más importantes que describen fallos en un entorno industrial. Uno de los aspectos más importantes del trabajo que se presenta es que manejó datos obtenidos de un ambiente de explotación real.
Este trabajo representa por primera vez la incorporación de conocimiento experto expresado en variables no numéricas a la selección de los rasgos más importantes para el diagnóstico de fallos de un componente industrial, en particular, de chumaceras. Los resultados alcanzados mostraron que la relevancia de los rasgos cualitativos que se incorporaron a la descripción de los fallos es superior a la de los rasgos numéricos.
De manera particular, los resultados alcanzados demostraron que el conjunto de datos derivados de las mediciones de las vibraciones realizadas en la dirección horizontal es el más importante para diferenciar los fallos tratados, pues las vibraciones de la dirección vertical solo ofrecen buenos resultados para diferenciar las clases BI y BIH. El orden en el que los fallos evidencian mayores posibilidades de clasificación es H-BIH, BI-BIH y BI-H.
AGRADECIMIENTOS
A grupo de diagnóstico de termoeléctrica Máximo Gómez de Mariel, en especial a los compañeros especialistas: Julio González Martínez, Yuritza Cruz Guzmán, Jorge C. Arce Miranda y María Antonia Téllez.
REFERENCIAS
A.Moosavian, 2013. Comparison of two classifiers; K-nearest neighbor and artificial neural network, for fault diagnosis on a main engine journal-bearing. Shock and Vibration , Issue 20, p. 263–272.
Babu, T. N., 2014. High Frequency Acceleration Envelope Power Spectrum for Fault Diagnosis on Journal Bearing using DEWESOFT. Research Journal of Applied Sciences, Engineering and Technology, 8(10), pp. 1225-1238.
Byungchul, J., 2014. Statistical Approach to Diagnostic Rules for Various Malfunctions of Journal Bearing System Using Fisher Discriminant Analysis. s.l., s.n.
El-Thalji, I., 2015. A summary of fault modelling and predictive health monitoring of rolling element bearings. Mechanical Systems and Signal Processing, pp. 252-272.
Khelf, I., 2013. Adaptive fault diagnosis in rotating machines using indicators selection. Mechanical Systems and Signal Processing, Issue 40, p. 452–468.
Lei, Y., 2013. A review on empirical mode decomposition in fault diagnosis of rotating machinery. Mechanical Systems and Signal Processing , Issue 35, pp. 108-126.
Ruiz-Shulcloper, J., 2002. Logical Combinatorial Pattern Recognition: A Review. Recent Research Developments in Pattern Recognition, Volume 3, pp. 133-176.
Saridakis, K., 2008. Fault Diagnosis of Journal Bearings Based on Artificial Neural Networks and Measurements of Bearing Performance Characteristics. Scotland, s.n.
Recibido: 15/10/2017
Aceptado: 19/10/2018