Meu SciELO
Serviços Personalizados
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares em
SciELO
Similares em
SciELO
Compartilhar
Revista Cubana de Ciencias Informáticas
versão On-line ISSN 2227-1899
Rev cuba cienc informat vol.12 supl.1 La Habana 2018
ARTÍCULO ORIGINAL
Metaheurística GRASP para el problema Vertex Bisection Minimization.
GRASP metaheuristics for the Vertex Bisection Minimization problem.
Jorge Moreno Ramírez1*
1Departamento de Ciencia de la Computación, Universidad Federal Fluminense, 24210-240, Brasil
*Autor para la correspondencia: jmoreno@ic.uff.br
RESUMEN
Dado un grafo no orientado G = (V, E), donde V denota el conjunto de vértices y E representa el conjunto de aristas, el problema Vertex Bisection Minimization consiste en particionar el conjunto V en dos subconjuntos B y B1, de manera que |B| = l|V |/2Jy se minimice el número de vértices en B que son adyacentes a algún vértice de B1. Este problema pertenece al conjunto de los problemas de diseño de grafos y tiene aplicaciones en áreas como optimización de redes, teoría de grafos, recuperación de información, etc. Este problema es NP-difícil sobre grafos en general, aunque polinomialmente soluble para árboles e hipercubos. Por su importancia, diversos enfoques heurísticos han sido realizados con el propósito de encontrar soluciones de calidad. En este trabajo fue desarrollada una metaheurística GRASP para abordar este problema.
Los resultados experimentales muestran que el algoritmo propuesto obtiene resultados de mejor calidad que los algoritmos heurísticos encontrados en la literatura para este problema.
Palabras clave: Metaheurística, GRASP, Bisección de vértices
ABSTRACT
Given a non-oriented graph G = (V, E), where V denotes the set of vertices and E represents the set of edges, the Vertex Bisection Minimization problem consists of partitioning V into two subsets B and B1, such that |B| = l|V |/2J and minimizing the number of vertices in B that are adjacent to some vertex of B1. This problem belongs to the set of graph layout problems and has applications in areas such as network optimization, graph theory, information retrieval, etc. This problem is NP-hard on graphs in general, but polynomially soluble for trees and hypercubes. Because of its importance, various heuristic approaches have been carried out with the purpose of finding quality solutions. In this work, a GRASP metaheuristics was developed to address this problem. The experimental results show that the proposed algorithm obtains better quality results than the heuristic algorithms found in the literature for this problem.
Key words: Metaheuristics, GRASP, Vertex Bisection
INTRODUCCIÓN
Los problemas de diseño de grafos aparecen con frecuencia en áreas como optimización de redes, diseño de circui- tos VLSI (Very Large Scale Integration ), teoría de grafos, recuperación de información, etc (Díaz et~al., 2002). Estos problemas son generalmente NP-difíciles, por lo que con frecuencia se recurre al uso de procedimientos heurísticos.
Dado un grafo G = (V, E), donde V representa el conjunto de vértices y E denota el conjunto de aristas, el problema Vertex Bisection Minimization (VBM) consiste en particionar el conjunto de vértices del grafo en dos subconjuntos B y B1, de manera que |B| = l|V |/2Jy se minimice el número de vértices en B que son adyacentes a algún vértice de B1(Díaz et~al., 2002). Este problema pertenece al conjunto de los problemas de diseño de grafos y ha sido abordado a través de métodos exactos y heurísticos al tratarse de un problema NP-difícil (Brandes and Fleischer, 2009). Un algoritmo exacto basado en ramificación y poda fue propuesto en (Jain et~al., 2016a) para el problem VBM. Ese algoritmo consiguió resolver instancias con grafos de hasta 24 vértices. Otro algoritmo exacto, pero basado en la Programación Lineal en Enteros es presentado en (Jain et~al., 2016b), resolviendo este problema en grafos de hasta 48 vértices. Desafortunadamente, el uso de algoritmos exactos se torna inviable sobre grafos de mayor tamaño. En ese sentido, varios algoritmos heurísticos han sido desarrollados para abordar este problema.
Algunas de las heurísticas para el problema Vertex Bisection Minimization están basadas en las heurísticas desarrolladas para el problema Graph Bisection. En ese problema, el objetivo es particionar el conjunto de vértices del grafo en dos subconjuntos, de manera que se minimice el número de aristas entre los subconjuntos. Entre las heurísticas desarrolladas para el problema Graph Bisection están una heurística basada en Simulated Annealing (Johnson et~al., 1989), un algoritmo genético (Bui and Moon, 1996), así como un procedimiento basado en la metaheurística Colonia de Hormigas (Aguilar, 2016).
Un algoritmo memético fue propuesto para el problema Graph Bisection en (Galinier et~al., 2011) con resultados relevantes para ese problema. En (Jain et~al., 2016c) se implementa una adaptación de ese algoritmo para el problema VBM denominada AMAGP. En ese mismo artículo se presenta un nuevo algoritmo memético para el problema VBM denominado MAVBMP. El algoritmo MAVBMP usa diferentes heurísticas para generar la población inicial, así como diferentes operadores de cruzamiento. Otro de los elementos incorporados es un operador de mejora, cuyo objetivo es mejorar una solución mediante intercambios de vértices. A pesar de esto, este operador contiene muchas restricciones para ser aplicado y como consecuencia no puede ser usado en varias situaciones.
La metaheurística GRASP (Greedy Randomize Adaptive Search Procedure ) ha sido usada exitosamente en nu- merosos problemas de optimización combinatoria (Mestria et~al., 2013; Díaz et~al., 2017). Esta metaheurística ha sido ampliamente estudiada y posee características deseables, como la posibilidad de ser implementada usan- do paralelismo y la simplicidad de su estructura. El objetivo de este trabajo fue desarrollar un procedimiento heurístico basado en la metaheurística GRASP que presente resultados competitivos con tiempos cortos de respuesta.
El resto de este documento está organizado como se explica a continuación. La siguiente sección describe los algoritmos implementados que constituyen la estructura básica de la metaheurística GRASP. A continuación son descritos los experimentos computacionales realizados y son analizados los resultados obtenidos. Finalmente, son presentadas las conclusiones del trabajo y las referencias bibliográficas del mismo.
Metaheurística desarrollada
La metaheurística Greedy Randomized Adaptive Search Procedure (GRASP) es un método para obtener so- luciones de buena calidad en problemas de optimización combinatoria (Resende and Ribeiro, 2016). GRASP puede definirse como un proceso iterativo, donde en cada iteración se realiza una fase de construcción y una búsqueda local.
En la fase de construcción, la idea es combinar un algoritmo ávido con una componente aleatoria. Los algorit- mos ávidos suelen ser generalmente iterativos, de manera que en cada iteración se seleccione el elemento que proporcione el mayor incremento de calidad a la solución que está siendo construida. Como consecuencia, este tipo de procedimiento no siempre obtiene el valor óptimo y en algunas instancias de problemas puede dar lugar a soluciones muy alejadas del valor óptimo. Este inconveniente es enfrentado por la metaheurística GRASP mediante la inclusión de una componente aleatoria en el procedimiento de construcción. La inclusión de esta componente aleatoria es realizada con el propósito de incorporar diversificación a las soluciones creadas, lo que pudiera conducir a buenos resultados.
Una vez que se genera una solución, la metaheurística GRASP emplea un procedimiento de búsqueda local. Este procedimiento consiste en buscar soluciones mejores en una vecindad de la solución generada en la fase constructiva. Este proceso de crear soluciones y realizar búsquedas locales se repite hasta alcanzar cierto criterio de parada establecido. Finalmente, el algoritmo devuelve como resultado la mejor solución encontrada entre todas las iteraciones.
Construcción de las soluciones iniciales
Para la construcción de las soluciones iniciales fueron utilizados dos métodos que son descritos a continuación. Ambos métodos están basados en la idea que los vértices en B deben tener la mayoría de sus vértices (o todos) adyacentes en B. El conjunto de vértices adyacentes a un vértice v y que pertenecen a un conjunto S ⊆ V se denotará como NS (v).
El Algoritmo 1 presenta el primero de estos métodos, denominado como Const_Inic1. Este método está basado en la heurística ávida H 1 (Jain et~al., 2016c), pero introduciendo el uso de una componente aleatoria. Esta componente aleatoria se encuentra en el proceso de selección del vértice que será adicionado al conjunto B. La heurística H 1 selecciona en cada paso el vértice con menor número de vértices adyacentes en V \ B. Para evitar esta selección golosa se crea una lista con aquellos vértices de B que tienen "pocos" vértices adyacentes en V \ B. Esto se conoce como Lista Restricta de Candidatos (LRC) y está condicionada a un parámetro α (línea 5). Si el parámetro α = 0 se estaría en presencia de una selección ávida o golosa. Por otro lado, si α = 1 se estaría en presencia de una selección aleatoria. Una vez creada la LRC, un elemento u ∈ B es seleccionado al azar de esta lista (línea 6). Después de seleccionar aleatoriamente un elemento u de la LRC e insertarlo en B, son analizados los vértices adyacentes a u que no están en B. Si todos los vértices adyacentes a u pueden ser adicionados a B, entonces estos vértices son insertados en B (línea 10). De no ser posible, se adicionan a B tantos vértices adyacentes de u como sea posible hasta que |B| = l|V |/2J (líneas 12-13).

El otro procedimiento utilizado en este trabajo para generar soluciones iniciales es mostrado en el Algoritmo 2, denominado como Const_Inic2. Este algoritmo comienza adicionando al conjunto B un vértice seleccionado aleatoriamente. En su ciclo principal (líneas 3-9), el algoritmo selecciona un vértice de la lista de candidatos LRC, creada con aquellos vértices de V \ B con "muchos" vértices adyacentes en B. A diferencia del algoritmo anterior, el algoritmo Const_Inic2 presenta un carácter ávido cuando α = 1 y un carácter aleatorio cuando α = 0. Como será mostrado más adelante, cada uno de los algoritmos Const_Inic1 y Const_Inic2 generará la mitad de las soluciones iniciales usadas por la metaheurística.

Búsqueda Local
Las soluciones generadas en la fase constructiva del GRASP pueden estar alejadas de la solución óptima. Por ese motivo es realizada una exploración por soluciones vecinas a la solución generada, con el objetivo de encontrar soluciones de mayor calidad.
La búsqueda local desarrollada en este trabajo usa la estrategia de best improvement. Esta estrategia consiste en actualizar la mejor solución encontrada con aquella solución vecina de mayor calidad.
Sea S = (B, B1) una solución para el problema VBM, una solución vecina S1 se obtiene a partir de S, intercambiando un vértice en B por un vértice en B1. Para cada vértice u ∈ B1 se calcula φ(u), que representa cuántos vértices podrían ser eliminados del valor de la solución al pasar el vértice u ∈ B1para el conjunto B. Posteriormente se calcula para cada vértice en v ∈ B el valor σ(v), que determina el número de vértices en B que serían adicionados al valor de la solución si se pasara v ∈ B para el conjunto B1. Finalmente se determina el par (v, u) ∈ (B, B1) que minimice el valor ψ(v, u) = φ(u) − σ(v). Si el par encontrado (v, u) ∈ (B, B1) satisface que ψ(v, u) > 0, entonces la solución S1= ((B \ {v}) ∪ {u},(B1\ {u}) ∪ {v}) será mejor que la solución S.
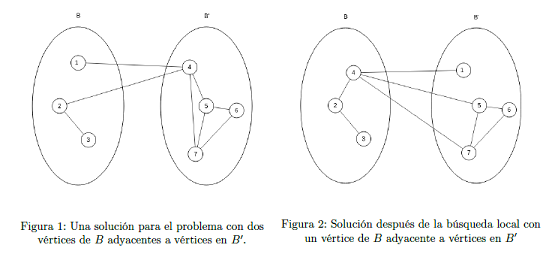
En (Jain et~al., 2016c) se propone un operador de mejora que también intercambia vértices entre los conjuntos B y B1pero con restricciones muy específicas. Dicho operador selecciona un vértice u ∈ B1 de manera que NBI (u) = ![]() . Ese vértice es intercambiado por un vértice v ∈ B tal que todos los vértices adyacentes a v son adyacentes a algún vértice en B1. La Figura 2 muestra un ejemplo de la búsqueda local usada en el GRASP. En este caso, el operador de mejora definido en (Jain et~al., 2016c) es incapaz de mejorar la calidad de la solución original mientras que la búsqueda local especificada en el Algoritmo 3 proporciona una solución mejor.
. Ese vértice es intercambiado por un vértice v ∈ B tal que todos los vértices adyacentes a v son adyacentes a algún vértice en B1. La Figura 2 muestra un ejemplo de la búsqueda local usada en el GRASP. En este caso, el operador de mejora definido en (Jain et~al., 2016c) es incapaz de mejorar la calidad de la solución original mientras que la búsqueda local especificada en el Algoritmo 3 proporciona una solución mejor.

MATERIALES Y MÉTODOS
Como se expuso anteriormente, la metaheurística GRASP consta de una fase constructiva y de una fase de búsqueda local. Estos métodos fueron definidos en las subsecciones anteriores y son integrados en la metaheurística GRASP como se muestra en el Algoritmo 4. Inicialmente son construidas una solución ávida usando el método Const_Inic1 y una solución ávida usando el método Const_Inic2. Una vez aplicada la búsqueda local sobre cada una de estas soluciones, es seleccionada la solución de mejor calidad (línea 7). Durante la primera mitad de las iteraciones son generadas soluciones usando el método Const_Inic1, mientras que en la segundad mitad de las iteraciones se utiliza el método Const_Inic2. En el ciclo principal, cada vez que es generada una solución, se realiza la búsqueda local usando el método Busqueda_Local (líneas 15-16). Si la solución S1obtenida en la búsqueda local es mejor que la mejor solución encontrada S*, entonces se actualiza el valor de S* con S1 (línea S17-18).

El parámetro α es incrementado en 0.1 cada ![]() iteraciones (línea 20). De esta forma se usan los valores α ∈ {0.1,0.2,0.3,0.4,0.5} y α ∈ {0.5,0.6,0.7,0.8,0.9} para Const_Inic1 y Const_Inic2 respectivamente. Esta selección del parámetro α está basada en el hecho de que para valores superiores a 0.5 el algoritmo Const_Inic1 presenta un comportamiento más aleatorio. Por su parte, el algoritmo Const_Inic2 presenta un comportamiento más aleatorio para valores inferiores a 0.5.
iteraciones (línea 20). De esta forma se usan los valores α ∈ {0.1,0.2,0.3,0.4,0.5} y α ∈ {0.5,0.6,0.7,0.8,0.9} para Const_Inic1 y Const_Inic2 respectivamente. Esta selección del parámetro α está basada en el hecho de que para valores superiores a 0.5 el algoritmo Const_Inic1 presenta un comportamiento más aleatorio. Por su parte, el algoritmo Const_Inic2 presenta un comportamiento más aleatorio para valores inferiores a 0.5.
RESULTADOS Y DISCUSIÓN
En esta sección se presentan los resultados experimentales obtenidos sobre varias de las instancias usadas en (Jain et~al., 2016c). Estos experimentos fueron desarrollados sobre un computador Intel (R) Core(TM) i3- 3110M CPU @ 2.40GHz, con 2 Gb de RAM sobre el sistema operativo Fedora 22. Todos los métodos fueron programados en el lenguaje C++ usando el compilador gcc y el número de iteraciones para el GRASP fue fijado en 100. La metaheurística GRASP fue comparada con los algoritmos AMAGP y MAVBMP, propuestos en (Jain et~al., 2016c) e implementados en MATLAB 7.0 sobre un computador Dual Xeon, 6 con 24GB de RAM. Las instancias usadas para analizar el comportamiento del GRASP son clasificadas como:
Grafos pequeños : consiste en 23 grafos del conjunto de 84 grafos disponible en http://www.optsicom.es/vsp. El número de vértices de estos grafos varía entre 16 y 24 mientras que el número de aristas varía entre 18 y 34.
Grafos Harwell-Boeing : un subconjunto de los grafos disponibles en la biblioteca de dominio público Matrix Market.
Grafos estándares : un conjunto de grafos conteniendo grafos bipartitos e hipercubos. Los grafos bipartitos poseen diferentes dimensiones, con grafos pequeños como K4,15 y otros de mayor tamaño como K100,100. Por su parte, los hipercubos analizados van desde Q3 hasta Q10.
La tabla 1 muestra los resultados obtenidos para los grafos pequeños. Estos resultados se corresponden con el mejor resultado obtenido después de 30 ejecuciones de cada algoritmo. Los tiempos presentados para cada uno se corresponden con el tiempo total empleado. En este conjunto de grafos todos los algoritmos comparados poseen un comportamiento similar. En negrita aparecen aquellos resultados obtenidos por un algoritmo que son estrictamente mejores que los resultados obtenidos por los otros algoritmos. Considerando este criterio, el mejor desempeño lo tiene GRASP, con una solución que supera en calidad a los otros algoritmos (instancia p52_20_27). Por otro lado, los tiempos usados por la metaheurística GRASP resultaron ser competitivos en relación a los otros algoritmos.
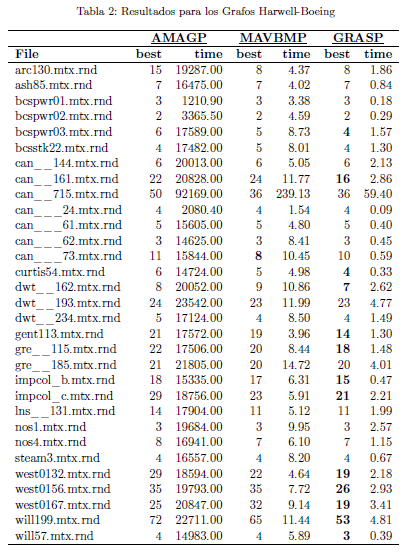
La Tabla 2 muestra los resultados obtenidos para los grafos Harwell-Boeing. Nuevamente en negrita están resaltadas aquellas soluciones de un algoritmo que mejoran a las soluciones obtenidas por los otros algoritmos. En este sentido, la metaheurística GRASP obtuvo el mejor desempeño. De acuerdo con la tabla, GRASP obtuvo 13 soluciones de mayor calidad que las obtenidas por los otros algoritmos. Solamente para la instancia can 73.mtx.rnd el algoritmo MAVBMP obtuvo un resultado superior.
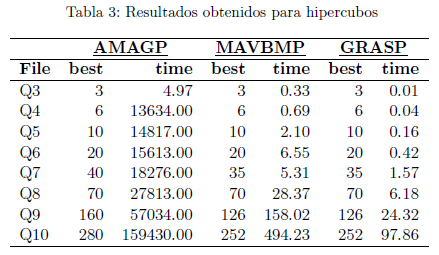
Para los hipercubos el valor óptimo para el problema VBM es conocido y dado el hipercubo Qn la solución para este problema viene dado por la expresión ![]() (Brandes and Fleischer, 2009). De acuerdo con la Tabla 3, en todos los casos los algoritmos MAVBMP y GRASP obtuvieron los valores óptimos, pero GRASP usa menos tiempo para alcanzar esos valores. En el caso de AMAGP, el desempeño no fue tan bueno sobre estos grafos y solo consigue encontrar los valores óptimos hasta el hipercubo Q6.
(Brandes and Fleischer, 2009). De acuerdo con la Tabla 3, en todos los casos los algoritmos MAVBMP y GRASP obtuvieron los valores óptimos, pero GRASP usa menos tiempo para alcanzar esos valores. En el caso de AMAGP, el desempeño no fue tan bueno sobre estos grafos y solo consigue encontrar los valores óptimos hasta el hipercubo Q6.
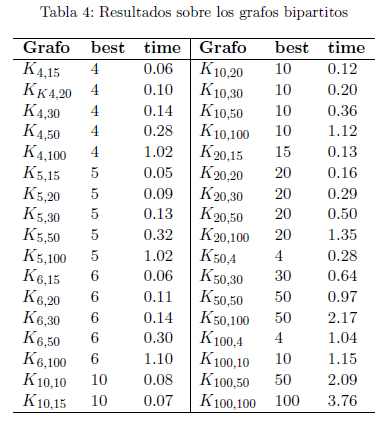
La Tabla 4 muestra los resultados sobre grafos bipartitos. Para estos grafos, todos los resultados obtenidos por GRASP se corresponden con los valores obtenidos por las heurísticas AMAGP y MAVBMP en (Jain et~al., 2016c). Los tiempos utilizados por esos algoritmos no son presentados en ese artículo.
En general, la metaheurística GRASP mostró un comportamiento superior a las otras heurísticas comparadas, tanto en términos de tiempo como en calidad de las soluciones. En resumen, 14 nuevas soluciones fueron encontradas. Cada una de estas soluciones representa un nuevo límite superior para la solución óptima del problema sobre estas instancias.
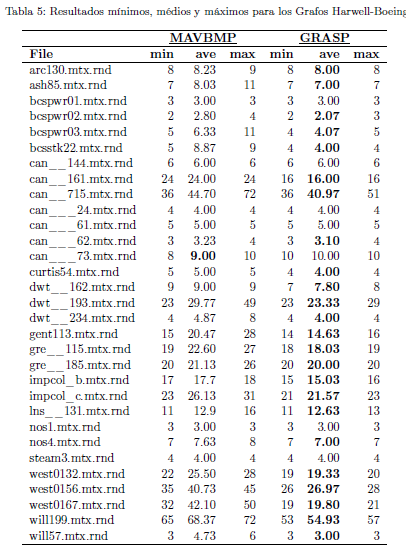
Debido a que las heurísticas comparadas en este trabajo cuentan con componentes aleatorias, los últimos experimentos fueron encaminados a explorar la estabilidad de sus soluciones. En particular, fueron analizados los resultados mínimos, medios y máximos obtenidos por los métodos MAVBMP y GRASP después de 30 ejecuciones. Estos experimentos fueron realizados sobre los grafos de las instancias Harwell-Boeing, pues es para estas instancias que son ofrecidos esos valores en (Jain et~al., 2016c). En la Tabla 5, las columnas 2, 3 y 4 representan los valores mínimos, medios y máximos obtenidos por el algoritmo memético MAVBMP, mientras que las columnas 5, 6 y 7 tienen el mismo significado pero para el algoritmo GRASP. Al analizar los resultados de esta tabla puede observarse como el algoritmo GRASP presenta los valores mínimos y máximos mucho más próximos de los valores medios que el algoritmo MAVBMP, indicando un menor error absoluto. En general, GRASP obtuvo resultados medios de mejor calidad en 24 grafos, mientras que MAVBMP solo obtuvo un resultado medio de mejor calidad que el algoritmo GRASP. Estos resultados apuntan a una mayor calidad y estabilidad en las soluciones obtenidas por el método GRASP.
CONCLUSIONES
En este trabajo se desarrolló una metaheurística GRASP para el problema Vertex Bisection Minimization. De acuerdo con la estructura básica del método GRASP, fueron diseñadas e implementadas las fases constructivas y de búsqueda local. Para comprobar la efectividad del algoritmo propuesto, fueron desarrollados experimentos sobre las instancias más usadas en la literatura para este problema. Los resultados obtenidos muestran que el algoritmo propuesto obtiene soluciones de buena calidad, superando a las mejores heurísticas encontradas para este problema en la literatura revisada. Por otro lado, el hecho de proporcionar rápidamente soluciones de buena calidad, hacen de este algoritmo un método apropiado para ser integrado en algoritmos exactos para la resolución del problema tratado.
AGRADECIMIENTOS
Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq)
REFERENCIAS BIBLIOGRÁFICAS
Aguilar, J. (2016). A general ant colony model to solve combinatorial optimization problems. Revista Colom- biana de Computación-RCC, 2(1).
Brandes, U. and Fleischer, D. (2009). Vertex bisection is hard, too. Journal of Graph Algorithms and Appli- cations, 13(2):119–131.
Bui, T. N. and Moon, B. R. (1996). Genetic algorithm and graph partitioning. IEEE Transactions on computers, 45(7):841–855.
Díaz, J., Petit, J., and Serna, M. (2002). A survey of graph layout problems. ACM Computing Surveys (CSUR), 34(3):313–356.
Díaz, J. A., Luna, D. E., Camacho-Vallejo, J.-F., and Casas-Ramírez, M.-S. (2017). Grasp and hybrid grasp- tabu heuristics to solve a maximal covering location problem with customer preference ordering. Expert Systems with Applications, 82:67–76.
Galinier, P., Boujbel, Z., and Fernandes, M. C. (2011). An efficient memetic algorithm for the graph partitioning problem. Annals of Operations Research, 191(1):1–22.
Jain, P., Saran, G., and Srivastava, K. (2016a). Branch and bound algorithm for vertex bisection minimization problem. In Advanced Computing and Communication Technologies, pages 17–23. Springer.
Jain, P., Saran, G., and Srivastava, K. (2016b). A new integer linear programming and quadratically constrained quadratic programming formulation for vertex bisection minimization problem. Journal of Automation Mobile Robotics and Intelligent Systems, 10.
Jain, P., Saran, G., and Srivastava, K. (2016c). On minimizing vertex bisection using a memetic algorithm. Information Sciences, 369:765–787.
Johnson, D. S., Aragon, C. R., McGeoch, L. A., and Schevon, C. (1989). Optimization by simulated annealing: an experimental evaluation; part i, graph partitioning. Operations research, 37(6):865–892.
Mestria, M., Ochi, L. S., and de Lima Martins, S. (2013). Grasp with path relinking for the symmetric euclidean clustered traveling salesman problem. Computers & Operations Research, 40(12):3218–3229.
Recibido: 04/06/2018
Aceptado: 10/09/2018