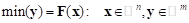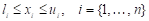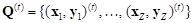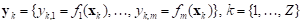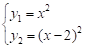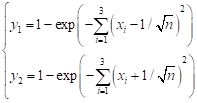INTRODUCCIÓN
En la industria moderna, la inmensa mayoría de los asuntos de diseño de sistemas y procesos, pasa por la solución de un problema de optimización. Como usualmente se requiere considerar, simultáneamente, varios criterios contradictorios, dicho problema de optimización es multiobjetivo. Este tipo de problemas puede resolverse integrando los diversos objetivos en uno solo, ya sea por agregación lineal o no lineal, por ordenamiento, o por otra técnica. Este enfoque, llamado a priori, que realmente transforma el problema multiobjetivo en uno uniobjetivo, tiene el inconveniente de que debe suministrarse cierta información sobre las preferencias con respecto a los objetivos, antes de proceder al proceso de optimización, siendo la materialización de estas preferencias usualmente subjetiva y poco realista (Ling et al, 2016; Yang at al., 2014; Olivares-Mendes et al., 2014).
Por el contrario, el llamado enfoque a posteriori, evita este problema al no requerir ninguna información previa acerca de la preferencia de los objetivos. En ella, el proceso de optimización conduce a un grupo de soluciones óptimas, que lo son en el sentido amplio de que ninguna otra, en el espacio de soluciones factibles considerado, mejora uno de los objetivos sin, a su vez, empeorar algunos de los otros (Purshouse et al., 2014). A este conjunto de soluciones se les llama no dominadas o conjunto de Pareto, y a su representación en el espacio de objetivos, frente de Pareto (Xiong et al., 2015; Bechikh et al., 2015). Una vez obtenido el frente de Pareto, se selecciona la solución más conveniente, teniendo en cuenta las condiciones reales del problema.
La literatura especializada refleja una gran diversidad de técnicas de optimización multiobjetivo a posteriori, siendo la inmensa mayoría de ellas heurísticas no basadas en el uso del gradiente de la función objetivo (Coello et al., 2007; Giagkiozis et al., 2015). Esto les confiere la importante ventaja, frente a los métodos numéricos basados en gradiente, de no requerir que dicha función objetivo cumpla un conjunto de requisitos matemáticos como la continuidad, la derivabilidad o la unimodalidad (Gong et al., 2015).
Dentro de las heurísticas para optimización multiobjetivo, el método de entropía cruzada se destaca por su capacidad para resolver problemas donde la probabilidad de encontrar la solución es particularmente baja (De Boer et al. 2005), lo que lo hace muy apropiado para situaciones donde el conjunto de Pareto está localizado en una parte muy pequeña del especio de búsqueda, sin gradientes marcados que lleven a él. Varias propuestas, en este sentido, has sido publicadas (Ünveren y Acan, 2007; Bekker y Aldrich, 2011; Hauman, 2012; Sebaa et al., 2013; Giagkiozis et al., 2014). Coautores de este trabajo, han participado en el desarrollo y la implementación de una heurística multi-objetivo basada en entropía cruzada, que ha demostrado simplicidad (en el sentido de requerir el ajuste de pocos parámetros) y efectividad en la solución de problemas complejos (Beruvides et al., 2016; Haber et al., 2017). Esta heurística, que ha sido aplicada con éxito a la solución de problemas prácticos (La Fé et al., 2018), está, sin embargo, implementada en MATLAB, lo que dificulta tanto su distribución (por el carácter propietario de MATLAB) como su incorporación a otros programas.
En consecuencia, se ha trazado como objetivo del presente trabajo, la implementación y comprobación de una biblioteca de clases, en lenguaje C++, que permita llevar a cabo la solución de problemas de optimización multiobjetivo, mediante una heurística basada en entropía cruzada. El trabajo se ha dividido en cuatro secciones. Luego de la presente introducción, se describe sucintamente el algoritmo utilizado y la implementación de la biblioteca y de una aplicación de prueba. La cuarta sección describe la comprobación de los resultados de la biblioteca y, para finalizar, se resumen las conclusiones y proyecciones de trabajo futuras.
MATERIALES Y MÉTODOS
Descripción del algoritmo
El algoritmo para optimización multiobjetivo con entropía cruzada simple (simple multi-objective cross-entropy, SMOCE) (Haber et al., 2017), se dirige a resolver el problema:
donde:
y que, además, puede encontrarse restringida por:
El núcleo del algoritmo de SMOCE es la población de trabajo, Q, la cual, en la t-ésima iteración:
está compuesta por Z soluciones 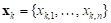 y sus respectivas funciones objetivo evaluadas, de forma que para el k-ésimo vector de variables, x
k
, el correspondiente vector de objetivos, y
k
, toma la forma:
y sus respectivas funciones objetivo evaluadas, de forma que para el k-ésimo vector de variables, x
k
, el correspondiente vector de objetivos, y
k
, toma la forma:
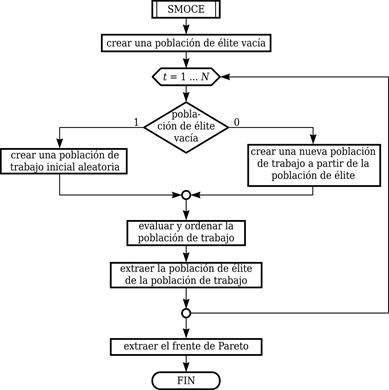
El proceso evolutivo (ver Fig. 1) tiene lugar en un ciclo con una única condición de término: el arribo al número máximo de generaciones, N. En la primera iteración, se crea una población de trabajo con valores de sus variables de decisión tomados aleatoriamente de una distribución uniforme entre sus respectivos valores mínimos y máximos. En cada una de las iteraciones siguientes, se crea una nueva población de trabajo, Q (t) , a partir de la de la iteración anterior, Q (t-1) . Esto se lleva a cabo evaluando cada solución de la población y ordenándolos según su dominancia (es decir, la cantidad de soluciones que la dominan), para extraer de ella los E=aZ mejores individuos, siendo 0≤a≤1, un parámetro del algoritmo denominado fracción de élite.
A partir de la población de élite, se crea un histograma donde la dimensión correspondiente a cada una de las funciones objetivos, se divide en D intervalos, por lo que las soluciones de élite se agrupan en D m clases. Para cada una de dichas clases, se crea una fracción de la nueva población, de tamaño proporcional a la cantidad de soluciones contenidas en la clase, y seleccionados aleatoriamente, a partir de una distribución normal con media y varianza igual a cada una de las variables de las soluciones de dicha clase, truncada a los valores mínimos y máximos de dicha variable.
Una vez concluido el proceso evolutivo, se extrae el frente de Pareto filtrando la población de élite resultante para eliminar todas las soluciones dominadas.
El nivel de complejidad, C, del algoritmo propuesto es similar al de otras heurísticas basadas en ordenamiento de Pareto, el cual está dado por la expresión (Coello et al. 2007 p. 317):
donde t es el tiempo de evaluación de la función objetivo, N es el número de iteraciones, Z es el tamaño de la población y m es la cantidad de funciones objetivos. Un estudio detallado de la eficiencia del algoritmo y, especialmente, de la influencia de sus parámetros en dicha eficiencia, ha sido previamente publicado por Haber y coautores (2017). Ese propio trabajo incluye, además, una comparación de los resultados obtenidos con la librería propuesta (MOCE+) con otras cinco heurísticas de optimización multiobjetivo: NSGA-II, MOEA/D, MOPSO, SPEA-II y PESA-II.
Descripción de la librería de clases
La librería de clases, denominada libGFO (gradient free optimization) incluye aquellas clases necesarias para llevar a cabo la optimización multiobjetivo con el método de entropía cruzada, aunque fue diseñada teniendo en cuenta su extensión futura a otras heurísticas.
En primer lugar, se diseñó la clase GFOVariable (Fig. 2), que representa a una variable de decisión, del problema de optimización. La misma cuenta con tres atributos: el nombre (cadena de caracteres) y los valores mínimo y máximo (numérico) que puede tomar la variable. La clase presenta, además, operaciones para acceder a y modificar los valores de dichos atributos.
La clase GFOVariables (Fig. 3) representa al conjunto de todas las variables de decisión del problema. Su único atributo es un listado de las instancias de GFOVariable. La clase cuenta con operaciones para agregar, modificar y eliminar variables de la lista.
La clase GFOObjective (Fig. 4) representa a los objetivos de optimización. Ésta cuenta con los atributos para almacenar el nombre y el tipo de objetivo (minimización o maximización) así como con las operaciones de acceso y modificación correspondientes.
De forma similar a la clase GFOVariables, GFOObjectives (Fig. 5) permite manipular el conjunto de las funciones objetivo del problema. Cuenta, como atributo, con un listado de instancias de la clase GFOObjective y con un conjunto de operaciones que permiten consultar y modificar dicho listado.
La clase GFOParameters (Fig. 6) permite representar el conjunto de pares nombre/valores que contienen los parámetros del algoritmo de optimización. Dicha clase contiene, como atributos, un listado de valores de cadena, para almacenar los nombres y otro listado, numérico, para los valores correspondientes. Cuenta, además, con un grupo de operaciones que permiten agregar, eliminar y consultar los valores de los parámetros, dado su nombre.
La clase abstracta GFOFunction (Fig. 7) permite definir la clase que servirá de base para cualquier función objetivo. La misma cuenta con una única operación abstracta, consistente en la evaluación de las funciones objetivos, tomando como argumento una matriz, con los valores de las variables de decisión y devolviendo otra matriz, con los valores de los objetivos.
Para la representación del algoritmo de optimización, se definió una clase base denominada GFOHeuristicBase, (Fig. 8) con el objetivo de, a través de clases derivadas, implementar las diversas heurísticas. La misma implementa las funcionalidades comunes a cualquier algoritmo de optimización. En primer lugar, dispone de los atributos públicos para manipular los parámetros, las variables de decisión y los objetivos del problema, así como de atributos privados para la función objetivo y el almacenamiento de la población. Cuenta, además, con operaciones para asignar y devolver la función objetivo y para devolver el frente de Pareto. También presenta una operación abstracta, para implementar la ejecución del algoritmo, en las clases derivadas.
Finalmente, se implementó la clase GFOHeuristicMOCE (Fig. 9), derivada de GFOHeuristicBase, para representar el algoritmo de optimización multiobjetivo, basado en entropía cruzada.La clase GFOHeuristicMOCE cuenta con un atributo para almacenar la población de élite. También dispone de operaciones para inicializar la población de trabajo, para extraer, de ésta, a la población de élite, y para crear la nueva población de trabajo a partir de la de élite.
Debe hacerse notar que, en varias de las clases antes descritas, se utiliza la clase DoubleMatrix, implementada en la biblioteca EcMatrix, que constituye una interfaz para el uso de las funcionalidades de operaciones con matrices proporcionadas por la biblioteca Eigen.
Aplicación para el uso de la librería
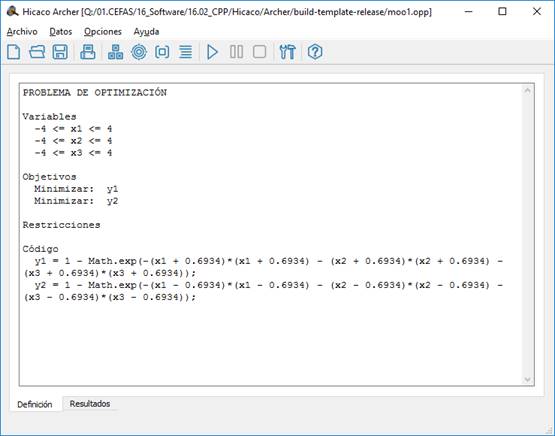
Con el propósito de comprobar tanto la funcionalidad de la librería desarrollada como su capacidad de integración en otros programas, se desarrolló una aplicación para optimización multiobjetivo, con interfaz gráfica de usuario. La aplicación (Fig. 10), denominada Hicaco Archer, fue implementada utilizando la plataforma Qt, con el objetivo de garantizar su portabilidad tanto a MS Windows como a Linux.
La aplicación permite, a través de cuadros de diálogo, especificar las componentes del problema de optimización: variables, objetivos, restricciones y código. Luego de ejecutado el proceso de optimización, presenta los resultados tanto en forma tabular como gráfica (representando la frontera de Pareto).
El código que relaciona las variables de decisión con las funciones objetivo y las restricciones, se implementa en Qt Script, el cual se basa en ECMAScript.
RESULTADOS Y DISCUSIÓN
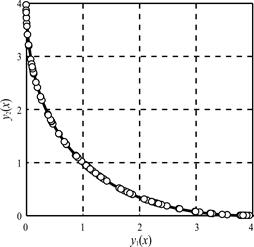
La eficacia es un criterio clave para evaluar las heurísticas de optimización multiobjetivo (Wang t al., 2015; Chen y Zou, 2014). Para analizar los resultados, se resolvieron tres problemas de optimización multiobjetivo, reflejados por la literatura (Huband et al., 2006). El primero de ellos (conocido en la literatura como MOP1), tiene dos objetivos a minimizar:
con una única variable de decisión, 10-3≤x≤103, sin restricciones.
Para la ejecución del mismo, se estableció una población de 500 soluciones, con una fracción de élite de 0,2; un número máximo de iteraciones de 100; y una cantidad de intervalos del histograma de 5. La Fig. 11 muestra la frontera de Pareto obtenida. La misma tiene un factor de hiperárea de 0.9981, lo cual significa que la frontera obtenida está muy cercana a la real.
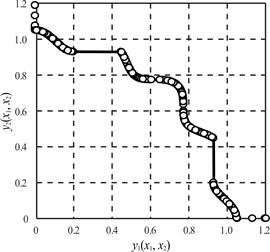
El segundo ejemplo considerado (denominado usualmente como MOP2), también tiene dos variables de decisión:
con tres variables de decisión, -4≤x 1, x 2, x 3≤4, y sin restricciones. Para el mismo, se establecieron como valores de los parámetros del algoritmo, los siguientes: tamaño de la población, 1000; factor de élite, 0,35; cantidad de iteraciones, 200; y cantidad de intervalos del histograma, 10. Los resultados obtenidos se muestran en la Fig.12. La razón de hiperárea correspondiente fue de 0.9999, mostrando una coincidencia casi perfecta con la frontera de Pareto real.
El tercer ejemplo (conocido como MOP4C), también considera dos objetivos:
pero con dos variables de decisión, -p ≤ x1, x2 ≤ p,y la restricción:
Para su ejecución, se estableció una población de trabajo de 5 000 soluciones, 200 iteraciones, 0,35 como factor de elitismo y 10 intervalos en el histograma. La Fig.13 muestra los resultados obtenidos. La relación de hiperárea de la frontera de Pareto obtenida fue de 0.9999, mostrando, al igual que en el ejemplo anterior, una coincidencia casi perfecta con la frontera real.
CONCLUSIONES
El principal resultado del presente trabajo ha sido la implementación de una biblioteca, en C++, para la optimización multiobjetivo utilizando el método de entropía cruzada. La misma se distribuirá como software libre y de código abierto, bajo la Licencia Pública General Reducida de GNU.
El funcionamiento de la biblioteca y su capacidad de integración a otros programas ha sido comprobado mediante el desarrollo de una aplicación con interfaz gráfica de usuario, para optimización multiobjetivo. Mediante la misma, se llevaron a cabo tres estudios de caso, basados en problemas de prueba para heurísticas de optimización multiobjetivo, tomados de la literatura especializada. En los tres casos, la frontera de Pareto obtenida mostró una excelente correspondencia con la frontera real, con valores de hiperárea superiores a 0,99.
Como desarrollos futuros del presente trabajo, se prevé la extensión de la biblioteca para incluir otras heurísticas no basadas en gradiente, tales como algoritmos genéticos, recocido simulado o algoritmo de hormiguero. También se prevé la implementación de facilidades de computación distribuida, que acelere el funcionamiento de los algoritmos, especialmente para problemas de alta complejidad.