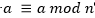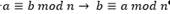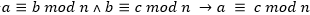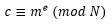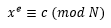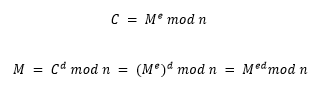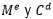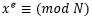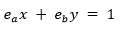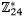Serviços customizados
Espanhol (pdf)
Artigo em XML
Referências do artigo
Enviar este artigo por email
Citado por SciELO 
Similares em
SciELO 
Permalink
INTRODUCCIÓN
Casi todos los algoritmos criptográficos, tanto cifrados simétricos como cifrados asimétricos son basados en la aritmética modular dentro de un número finito de elementos. La mayoría de los conjuntos infinitos que usamos son el conjunto de números naturales ℕ o el conjunto de números reales ℝ. En este estudio presentamos a la aritmética modular como un mecanismo de seguridad y vulnerabilidad sobre un conjunto finito de enteros ℤ para la criptografía asimétrica RSA.
La aritmética modular
Tal como define (Koscielny et al., 2013), sean a, b y n números naturales (a, b, nϵ ℕ; n= 0). Si dos enteros, a y b, tienen el mismo resto cuando se dividen entre n entonces se dice que son congruentes módulo n. Denotamos esto por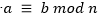 
. En símbolos:
La relación de congruencia es una relación de equivalencia, para todos los números naturales 𝑎, 𝑏, 𝑐, 𝑛 la relación de congruencia, denotada por ≡ , tiene las siguientes propiedades:
reflexividad 
simetría: 
transitividad: 
Debido a las propiedades de las relaciones de equivalencia, cada relación de congruencia módulo n determina una partición del conjunto de números naturales en clases de equivalencia disjuntas. Estas clases están formadas por números naturales congruentes módulo n. Para cualquier clase de equivalencia de a, existe algún a0 del conjunto {1,2,…, n-1}, tal que 
. En la que a0 se llama representación canónica de la clase de equivalencia de a (la clase [a]). El conjunto 
se llama conjunto de números naturales módulo n (Koscielny et al., 2013).
Definición 1 (El anillo de entero Zn). Sea el conjunto , en la cual definimos dos operaciones + y − para todos los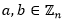 
de modo que (Paar and Pelzl, 2010):
Definición 2 (Grupo de clase de residuos primos módulo n, Z*n). Por lo tanto, los elementos del grupo de unidades de Zn son representados por los números primos a n (Delfs and Kneb, 2007).
Se llama el grupo de clase de residuo primario módulo n. La cantidad de elementos en Z*n (también llamado el orden de Z*n) es el número de enteros en el intervalo[1, n-1] que son primos para n.
Para un número natural n positivo fijo, se cumple la siguiente implicación:
en la cual r es el resto de a módulo n.
Deje que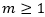 
sea un entero, decimos que los enteros a y b son congruente módulo m, si su diferencia a-b es divisible por m. Nosotros escribimos 
para indicar que a y b son congruentes módulo m. El número m se llama módulo (Hoffstein et al., 2008).
Tal como define (Kurose and Ross, 2013), las formulas de la aritmética modular para sumar y multiplicar se facilita con las siguientes igualdades:
La suma, la resta y la multiplicación se comportan de la misma manera que para residuos, o que para la aritmética de enteros. Lo habitual es tener leyes de identidad, conmutativas y distributivas, de modo que el conjunto de clases de residuos forme un anillo, denotado por Zn, para el módulo N. Por lo tanto; las leyes sobre el anillo se definen como (Tilborg and Jajodia, 2011):
La noción de los números primos, tal como manifiesta (Pace, 2012), son números mayores que 1, que son exactamente divisibles solo por 1 y ellos mismos, tienen una larga historia en matemáticas. Los números primos corresponden estrechamente a la noción de números atómicos, números que no pueden ser construidos como un producto de números más pequeños. Aunque fueron estudiados por los griegos desde la antigüedad, se han encontrado aplicaciones prácticas muy recientemente. Hoy en día, los números primos juegan un papel crucial en los algoritmos de encriptación, y la compra segura en línea en una tienda virtual, no sería posible sin ellos.
Los enteros a y b son primos relativos si y sólo si, mcd(a , b) = 1, los enteros a1, a2, a3, …, an son primos relativos en pares si y sólo si, el mcd(ai , aj) = 1, para todos los enteros i y j con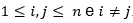 
.
Según (Dooley, 2018), un campo finito es una estructura algebraica con varias características. Primero, hay un conjunto de números que componen los elementos del campo. Utilizaremos un conjunto de enteros positivos {0, 1, 2, 3, …, p - 1} donde p es un número primo o una potencia de un número primo. Habrá exactamente p elementos en el conjunto, esto se llama el orden del campo. También declararemos dos operaciones + y x, que generalmente se llaman suma y multiplicación, y las restringiremos de modo que si a, b están en el conjunto de enteros, entonces también lo está a + b; esto se llama la propiedad de la cerradura del álgebra, por lo cual garantizamos que esto funcionará realizando el módulo de las sumas y multiplicaciones de p.
Según (Smart, 2016), sobre el teorema de los números primos, antes de analizar estos algoritmos, debemos analizar algunas heurísticas básicas sobre números primos. Un famoso resultado en matemáticas, conjeturado por Gauss, después de un extenso cálculo a principios de 1800, es el teorema del número primo que se expresa como el teorema 1.
Teorema 1 (Teorema de los números primos). La función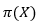 
cuenta con un número de primos menores que X, de donde tenemos la aproximación
Esto significa que los números primos son bastante comunes. Como muestra, el número de primos menores que 21204 es aproximadamente 21204 . El teorema del número primo también nos permite estimar la probabilidad de un número primo aleatorio, si p es un número elegido al azar, entonces la probabilidad de que sea primo es aproximadamente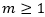
Según (Koblitz, 1994), hay muchas situaciones en las que uno quiere saber si un número n es primo en el criptosistema de clave pública RSA, y en varios criptosistemas basados en el problema del logaritmo discreto para campos finitos. Una primera interpretación de lo que esto significa es elegir un número entero impar grande n0 usando un generador aleatorio de dígitos y luego probando n0, n0 + 2,… para la primalidad hasta que obtengamos el primer primo que es menor a n0. Un segundo tipo es el uso de la prueba de primalidad para determinar si un entero especial de cierto tipo es primo.
El lema de Euclides manifiesta que para todos los enteros a, b y c, si mcd (a , c) = 1 y si a|bc, entonces a|b (Epp, 2019).
Un método para calcular el máximo común divisor de dos enteros es mediante el algoritmo euclidiano, que es un algoritmo antiguo, conocido y eficiente para encontrar el máximo común divisor. El algoritmo euclidiano mostrado en el algoritmo 1, Tabla 1, se basa en el hecho de que si r = a (mod b) , entonces:
si mcd (a , b) = si mcd (b , r)
Para todos los enteros , si mcd (a , m) = 1, entonces existe un entero s tal que . El entero s se llama el inverso de a módulo m. Una extensión del algoritmo de Euclides se define como, si a y b son primos relativos enteros, es decir mcd (a , b) =1, entonces existen los enteros s y t tal que a X s + b X t = 1 (Epp, 2019).
El teorema de la cancelación para la congruencia modular se define para todos los enteros a, b, c y n con n > 1, si mcd(c,n)=1 y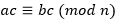 
, entonces . Para todos los enteros a, b y c, si mcd (a,c) = 1 y ab|c , entonces a| (Epp, 2019).
Ahora el pequeño teorema de Fermat se define si, p es cualquier número primo y a es cualquier entero tal que 
. Según (Joye and Tunstall, 2012), la operación principal del esquema de la firma RSA es una exponenciación modular en 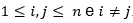. Es decir, una firma s se genera a partir de un mensaje m al computar 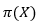, donde d es la clave privada, N es el producto de dos números primos grandes, y 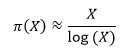es una función de relleno apropiada. Esta firma se puede verificar marcando si 
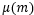es igual a 
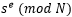. Definimos 
donde 
es la función de Euler.
Según manifiesta (Biggs, 2008), la función 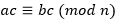se define para cualquier entero positivo x, como la cantidad de números enteros x en el rango 
, tal que su mcd (x, n) = 1, que se denota por . Se desprende de lo declarado que 
es también el número de elementos invertibles de Zn. El conjunto de enteros en las operaciones de suma y multiplicación con módulo n, es un anillo que lo denotamos por Zn. En general, no todos los elementos distintos de cero de Zn tienen un inverso multiplicativo, un elemento distinto de cero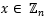 
tiene un inverso multiplicativo 
, si y solo si mcd (x, n) = 1.
Rivest-Shamir-Adleman (RSA)
Tal como afirma (Vaudenay, 2006), RSA es el primer criptosistema de clave pública que todavía es seguro y es usado, y que fue inventado por Ronald Rivest, Adi Shamir y Leonard Adleman, cuyas iniciales llevaron al nombre del criptosistema RSA. Fue publicado en 1978 según la referencia (Rivest et al., 1978), en la revista Communications de la ACM. Desde entonces, este algoritmo se ha adaptado, generalizado y transformado en varios estándares.
RSA es el cifrado asimétrico más conocido y utilizado, este se utiliza en una variedad de protocolos diferentes en el mundo de la seguridad informática, tal como el SSL1, CDPD2, y PGP3. RSA se ha usado en muchas aplicaciones diferentes hasta la fecha, y es probable que se use en muchas aplicaciones en el futuro (Daswani et al., 2007).
La aplicación de la aritmética modular a la criptografía RSA, define que para un texto plano, M, este se convierte en el texto cifrado, C, donde para 𝑒 se cumple que el 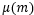, donde e debe estar entre 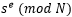, la ecuación que cifra el mensaje es la siguiente:
Para descifrar el mensaje, se necesita calcular un número d que es un inverso positivo al e módulo (p - 1)(q - 1), esto se expresa como :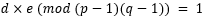 
. La fórmula para obtener el texto plano, M, se muestra a continuación:
Según (Delfs and Kneb, 2007), el criptosistema RSA se basa en hechos de la teoría de números elementales, que se conocen desde hace 250 años. Para implementar un criptosistema RSA, se tienen que multiplicar dos números primos muy grandes y hacer público su producto 𝑛, que es parte de la clave pública, mientras que los factores de n se mantienen en secreto y se utilizan como la clave secreta. La idea básica es que los factores de 𝑛 no se pueden recuperar de n, de hecho, la seguridad de la función de cifrado RSA depende tremendamente de la dificultad de la factorización, pero esta equivalencia no está probada.
Según (Kranakis, 1986), fue solo recientemente que la criptografía de clave pública se convirtió en una precisa asignatura matemática, principalmente como respuesta a la creciente necesidad de seguridad en la transmisión de información a través de los medios electrónicos, la principal nueva idea era basar la seguridad de los criptosistemas en la intratabilidad del número.
Tal como afirma (Salomaa, 1996); el texto sin formato o texto nativo se codifica como un número decimal, o podemos utilizar igualmente la representación binaria si queremos, el número se divide en bloques de tamaño adecuado, los bloques están encriptados por separado. Un tamaño adecuado para los bloques es el número entero único i, que satisface la desigualdad ; en algunos casos, uno puede elegir i - 1 como el tamaño del bloque, o asegurarse de que cada bloque sea menor que n, si la unicidad del descifrado es importante.
Tal como manifiesta (Daras and Rassias, 2015), en algunas aplicaciones, el mensaje m se cifra como 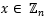se hace público. Recuperar m de , o verificar las propiedades de m es el problema.
El criptosistema RSA es un criptosistema de clave asimétrica donde dos claves, una clave pública y una clave privada son usados. La clave pública se utiliza para el cifrado y la clave privada se utiliza para el descifrado (Nisha and Farik, 2017).
El criptosistema de clave pública RSA se resume en la Tabla 2. La clave secreta de Bob es un par de primos grandes p y q. Su clave pública es el par (N, e) que consiste del producto N = p x q y un exponente de cifrado e que es primo relativo a (p - 1) x (q - 1) . Alice toma su texto sin formato y lo convierte en un entero m entre 1 y N. Ella cifra m calculando la cantidad
El número entero c es su texto cifrado, que le envía a Bob. Bob resuelva la congruencia 
para recuperar el mensaje m de Alicia, porque Bob conoce la factorización N = p x q. Eva, por otro lado, puede interceptar el texto cifrado c, pero a menos que ella sepa factorizar N, presumiblemente tiene dificultad para tratar de resolver la congruencia
En el algoritmo RSA existen dos componentes interrelacionados que son la elección de la clave pública y privada. Recordar que el algoritmo RSA es un cifrador de bloque en el que el texto nativo y el texto cifrado son enteros entre 0 y n -1, para algún n. Para un texto nativo M, el cifrado C, y el descifrado M, se realiza
Ambos; tanto el emisor como el receptor deben conocer el valor de n y el valor de e. Solo el receptor conoce el valor de d. El algoritmo de clave pública genera una clave pública KU = {e, n}, y una clave privada de KR = {d, n}, además este algoritmo de cifrado de clave pública debe cumplir las siguientes propiedades:
Es posible encontrar valores de e, d y n tales que
, para todo M< n.Es relativamente fácil calcular
para todos los valores de M< n.Es impracticable determinar d dado e y n.
Según (Stallings, 2014), los dos primeros requisitos son fáciles de satisfacer. El tercer requisito se puede satisfacer con valores altos de e y n. Según (Hoffstein et al. ,2008), la seguridad de RSA depende de la siguiente dicotomía:
Partida: Sea p y q números primos grandes, y N = p x q, y que e y c sean enteros.
Problema: Resuelva la congruencia
para la variable x.Solución: Bob, que conoce los valores de p y q, puede resolver fácilmente x como descrito en la Proposición 1.
Dificultad: Eva, que no conoce los valores de p y q, no puede encontrar fácilmente x.
Dicotomía: Resolver
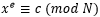es fácil para una persona que posee cierta información adicional, pero aparentemente es difícil para todas las demás personas.
Proposición 1. Sea p y q primos distintos y que e >= 1 y satisfaga
mcd(e,(p-1)x(q-1))=1
Sabiendo que e tiene un módulo inverso a (p - 1) x (q - 1) , digamos 
Entonces la congruencia
tiene la solución única
La (Figura 1), presenta el funcionamiento del algoritmo RSA, este algoritmo no se puede usar directamente, ya que se describe en un formato matemático, su configuración se establece la de la siguiente forma (Vaudenay, 2006):
Parámetro público: un entero par s.
Configuración: encuentre dos números aleatorios primos diferentes p y q de tamaño
bits. Establecer N = p x q. Elija un e aleatorio hasta que . Establecer d = 
Mensaje: un elemento
.Clave pública:
Clave secreta:
Cifrado:
.Descifrado:
.
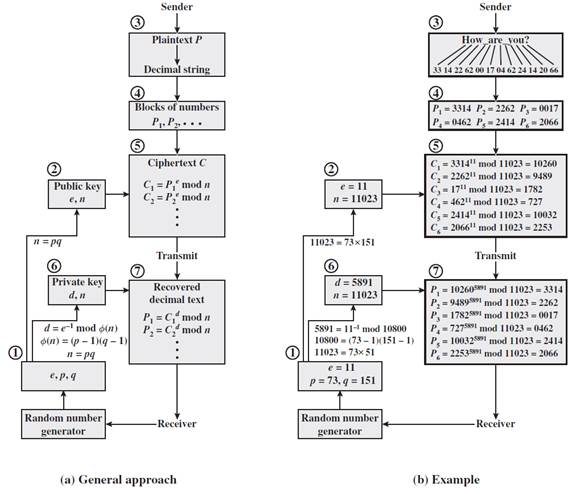
Fig. 2 Procesamiento de bloques múltiples en RSA, (a) Enfoque general y (b) Ejemplo de ejecución (Stallings, 2014).
Seguridad y ataques del sistema RSA
En la criptografía moderna a menudo emplea la frase del problema de la matemática computacionalmente difícil, un problema computacional se considera difícil o intratable o inviable si no existe un algoritmo conocido que resuelva todas las instancias del problema con un polinomio superior limitado a los recursos requeridos, en particular el tiempo polinómico. Cualquier criptosistema, cuya seguridad se basa en un problema insoluble se considera segura (Koscielny et al., 2013).
En 1991, se inició un concurso mundial, el RSA Factoring Challenge, organizado por la RSA Security para estimular a la comunidad científica a estudiar eficientemente los algoritmos para factorizar enteros grandes.
Se publicó una lista de números, que fueron los productos de dos primos. Estos números se llamaron números RSA. Se ofreció un premio en efectivo por factorizar algunos de ellos, tal como se muestra en la Tabla 3, el concurso duró dieciséis años y se cerró oficialmente en mayo del 2007 (Koscielny et al., 2013).
Según (Johnsonbaugh, 2018), la seguridad del sistema RSA para cifrar se basa principalmente en el hecho de que, hasta ahora, no se cuenta con un algoritmo eficiente para factorizar enteros; es decir, no se conoce un algoritmo para factorizar enteros de d dígitos en tiempo polinomial, O(dk)
La notación big-𝑂 se usa para el rendimiento y/o la complejidad de ejecución de un algoritmo, y la criptografía no es ajena a utilizar esta notación asintótica, más aún cuando se mide el rendimiento de este en un tiempo de ejecución exponencial, (Koblitz, 2004) define que para todo n > n0, dos funciones f(n) y g(n) están definidos y toman valores positivos, y para cierta constante C, se satisface la desigualdad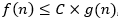 
entonces decimos que f = O(g).
Tal como (Parthajit, 2018) manifiesta que factorizar el producto de dos números primos grandes es la forma directa de atacar a RSA, toda la seguridad de RSA depende de la dificultad de factorizar. Técnicamente hablando, dado n como un entero de b bits, toda la factorización de los algoritmos toman un tiempo del orden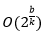 
, para todas las instancias de un k razonablemente pequeño, entonces afirmamos que RSA es seguro.
Los ataques contra RSA desde que se inventó en 1977, suelen explotar las debilidades en la forma en que se implementó RSA en sí, y podemos considerar tres tipos de ataques generales:
Ataques de protocolo
Los ataques de protocolo aprovechan las debilidades en la forma en que se utiliza RSA. Ha habido varios ataques de protocolo a lo largo de los años. Entre los más conocidos están los ataques que explotan la maleabilidad de RSA.
Según (Paar and Pelzl, 2010), en criptografía se dice que un esquema es maleable, si el atacante es capaz de transformar el texto cifrado en otro texto cifrado que conduce a una transformación conocida del texto sin formato. Tenga en cuenta que el atacante no descifra el texto cifrado, sino que simplemente es capaz de manipular el texto sin formato de manera predecible. Esto se logra fácilmente en el RSA si el atacante reemplaza el texto cifrado y por 
, donde s es un número entero y 
. El receptor descifra el texto cifrado manipulado y obtiene el texto nativo x, multiplicado por un factor s, si calcula lo siguiente:
Aunque el atacante no puede descifrar el texto cifrado, tales manipulaciones específicas todavía puede causar daño. Si x fuera una cantidad que debe transferirse, eligiendo s =2, el atacante podría duplicar exactamente la cantidad de una manera que el receptor no la detecta.
Una posible solución a todos estos problemas es el uso de relleno, que incorpora una estructura aleatoria en el texto sin formato antes del cifrado y evita los problemas anteriores mencionados. Técnicas modernas como el cifrado asimétrico óptimo de relleno (Asymmetric Encryption Padding - OAEP) para rellenar mensajes RSA, son específicos y estandarizados para la criptografía de clave pública estándar # 1 (PKCS # 1)
Ataques matemáticos
Según (Paar and Pelzl, 2010), el mejor método criptoanalítico matemático que conocemos es factorizar el módulo. Si un atacante conoce el módulo n, la clave pública e y el texto cifrado y, y su objetivo es calcular la clave privada d, que tiene la propiedad que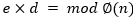 
; este simplemente podría aplicar el algoritmo euclidiano extendido y calcular d. Sin embargo, no conoce el valor de 
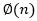. En este punto viene la factorización, la mejor manera de obtener este valor es descomponer n en sus factores primos p y q. Si el atacante puede hacer esto, el ataque tiene éxito en tres pasos:
Tal como expresa (Gómez, 2013), las claves RSA a menudo son generadas por un tercero confiable, se consideró una posibilidad que en los primeros tiempos de RSA se compartieran claves con el mismo módulo n, cada una con un diferente exponente de cifrado como de descifrado. Sin embargo, esto lleva a una ruptura total del esquema RSA, no solo para un cifrado simple, sino también para otras versiones más potentes del mismo, esto permite que cualquier usuario de una de estas claves pueda recuperar la clave privada de cualquier otro usuario mediante el algoritmo probabilístico Las Vegas, y el algoritmo de recurrencia de Miller, ya que para las entradas (n, e, d), estos producen la factorización de n.
Según (Rubinstein, 2010), la forma más obvia de atacar a RSA es factorizar el módulo n. Si Eva puede aprender los primos p y q con p x q = n, entonces ella puede calcular el exponente de descifrado d. Para hacer esto, supongamos que ella sabe n, p, q y e. Recordemos que d es elegido tal que 
. Como ella sabe p y q, ella puede calcular fácilmente 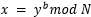. Luego usa el algoritmo euclidiano para encontrar d y a tal que 
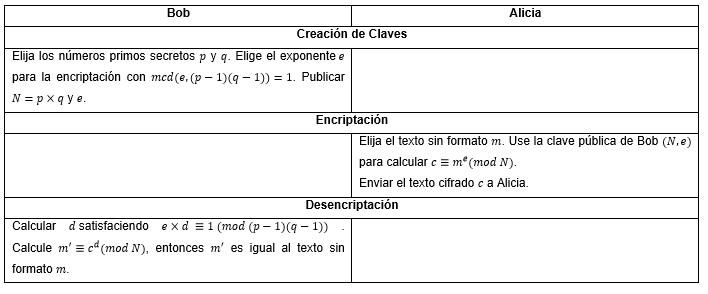; solo d importa aquí, y ella puede ignorar a.
Tal como expresa (Lenstra et al., 2012) en su artículo demostró que es posible romper RSA con bastante frecuencia en la práctica al calcular muchos máximos común divisores. Para hacer esto, ellos recolectaron 4.7 millones de módulos RSA y calcularon los máximos común divisores de cada par de módulos. Siempre que el máximo común divisor de ese par era 1, no había nada en ese cálculo, pero cuando el máximo común divisor era mayor que 1, este será un factor de ambos módulos. Asumiendo que los módulos no son idénticos, el máximo común divisor debe ser un factor primo de ambos módulos; calcular el otro factor era entonces sencillo. Usando esta técnica, pudieron romper alrededor del 0.2% de las claves RSA.
Ataques de canal lateral
Estos ataques explotan la información sobre la clave privada que se filtra a través de canales físicos, como el consumo de energía y su comportamiento a través del tiempo. Para observar tales canales, el atacante generalmente debe tener acceso directo a la implementación del RSA, que puede ser mediante una celda telefónica o una tarjeta inteligente.
Según (Paar and Pelzl, 2010), estos ataques de canal lateral son un campo grande y activo de investigación en criptografía moderna, y se dan generalmente en la traza de la potencia de un microprocesador cuando ejecuta el RSA, más precisamente, en el consumo de corriente eléctrica en el tiempo. El objetivo es extraer la clave privada d que se utiliza durante el descifrado del RSA. Este ataque específico se clasifica como análisis de potencia simple o SPA. Hay varias contramedidas disponibles para prevenir este ataque. Una simple es ejecutar un multiplicador con variables ficticias, después de una onda cuadrada que corresponde a un exponente bit 0. Esto da como resultado un perfil de potencia, y un tiempo de ejecución que es independiente del exponente.
Vulnerabilidad del sistema RSA
Según (Dong and Chen, 2012), el cifrado RSA es un algoritmo criptográfico ampliamente utilizado, y dado que no es poco común que el texto plano sea conocido parcialmente en la aplicación del RSA, ahora es ampliamente aceptado que el cifrado RSA debería evitar el uso de un exponente pequeño de cifrado. De otra manera, si existe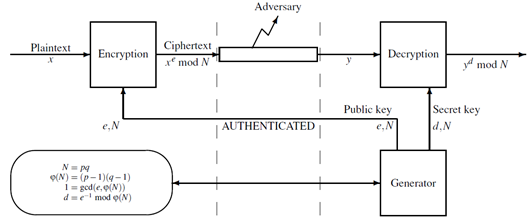 
, se puede encontrar el mensaje m eficientemente extrayendo la raíz e-ésima en enteros del texto cifrado .
Tal como afirma (Koscielny et al. ,2013), la velocidad del sistema criptográfico RSA no es impresionante. En el caso de parámetros de 1024 bits, incluso cuando hay circuitos integrados especiales dedicados particularmente a las necesidades de cifrado RSA, el algoritmo sigue siendo más lento que DES por un factor de 100 a incluso 1000. La exponenciación modular, es decir, exponenciación de enteros módulo n, es la operación más costosa ya que para una base de k bits y un exponente de k bits la multiplicación O(k) y su cuadratura deben ejecutarse.
Debido a su complejidad temporal, el algoritmo RSA rara vez se utiliza para el cifrado de datos, pero se puede aplicar para cifrar y transportar una clave de sesión para ser usado en la encriptación de datos por medio de algún algoritmo simétrico, como AES7 o 3DES8. Por esta misma razón, el criptosistema RSA tiene aplicaciones limitadas en tarjetas con chip, ya que la mayoría de los microprocesadores no pueden realizar cálculos con claves largas de 1024 bits. En la práctica, generalmente se aplican pequeñas claves públicas que lo hacen más vulnerables, el descifrado y verificación de firmas es mucho más rápido en tales casos.
Tal como afirma (Johnsonbaugh, 2018), otra manera posible de interceptar y descifrar un mensaje sería tomar la raíz n de c mod z, donde c es el valor cifrado y a es el valor a transmitir. Como 
, la raíz n de c mod z daría a, el valor descifrado, hasta ahora no hay implementaciones de un algoritmo para calcular las raíces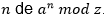 
.
La seguridad del sistema de cifrado RSA se basa principalmente en el hecho de que actualmente no existe un algoritmo eficiente conocido para factorizar enteros; es decir, actualmente no hay un algoritmo conocido para factorizar enteros de d bits en tiempo polinomial, O(Dk)
METODOLOGÍA COMPUTACIONAL
El algoritmo RSA, empieza por seleccionar dos números primos, p y q, y calcular su producto n, que es el módulo para el cifrado y el descifrado. Luego necesitamos la cantidad 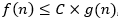, que se conoce como totalizador de Euler de n, que es el número de enteros positivos menores que n y primos relativos de n. Entonces, se selecciona un entero e que es primo relativo de 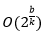, es decir, el máximo común divisor de e y , es 1. Finalmente, se calcula d tal que . En la (Figura 2), expresamos el procesamiento de bloques múltiples usando el algoritmo asimétrico RSA, su enfoque general y su ejecución.
Seleccionamos p = 37 y q = 71, donde p y q deben ser ambos primos,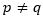
.
Calculamos n = p x q = 2627.
Calculamos el totalizador de .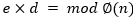
Seleccionamos un entero e, de modo que 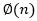, entonces, mcd(2520,17) = 1, de donde se obtiene e = 17, donde .
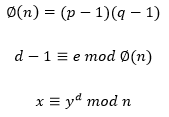Calculamos d, de manera que , entonces, d x 17 mod 2520 = 1, de donde se obtiene d = 593.
Clave pública KU = 
.
Clave privada 
.
El texto nativo M = m1m2m3 = 258566522, dividimos en 3 bloques de 3 dígitos cada uno:
m1 = 258
m2 = 566
m3 = 522
, donde M<n.
Texto cifrado por bloques: C = c1c2c3, aplicado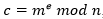 
, se tiene:
Texto cifrado por bloques obtenido: C = c1c2c3
C1 = 813
C2 = 1840
C3 = 1619
Texto nativo por bloques: M = m1m2m3, aplicando 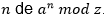, se tiene:
donde el mensaje nativo es M = m1m2m3 = 258566522.
El problema del módulo común en la seguridad del sistema RSA
Suponemos que dos entidades, Alicia y Bob usan claves públicas RSA con el mismo módulo n, pero con diferentes exponentes públicos ea y eb. El primer problema de seguridad que tenemos es que Alicia puede descifrar el mensaje enviado por Bob, esto sucede ya que dado un módulo n, un exponente público ea, y la correspondiente clave privada da, es posible recuperar la factorización de n = p X q. Entonces Alicia usa la factorización de n para recuperar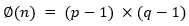 
y calcular la clave privada de Bob db con la ayuda de su exponente público eb.
El segundo problema de seguridad es que, si existe un atacante activo como Eva, ella puede descifrar el mensaje enviado a Alicia y a Bob, siempre y cuando su 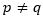, esto sucede ya que si 
, Eva puede calcular dos enteros 𝑥 e 𝑦 mediante la ecuación
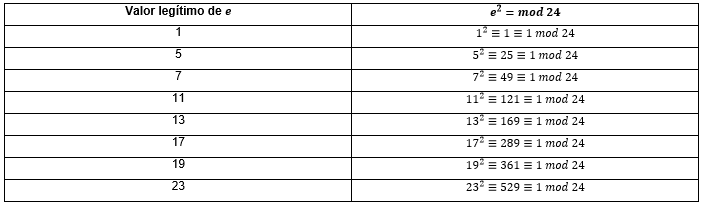
usando el algoritmo extendido de Euclides. Luego Eva usa los dos textos cifrados Ca y Cb, y calcula el texto plano m de la siguiente manera:
Este problema de vulnerabilidad consiste en que el criptoanalista realiza el cifrado repetido del texto cifrado, esto puede suceder incluso para un criptosistema de aspecto seguro, puesto que el texto sin formato se recupera, esto es un defecto fatal del esquema RSA. Sea un módulo RSA n = p X q = 35, m un texto sin formato y c el correspondiente texto cifrado, se va comprobar que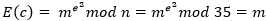 
, para cualquier exponente público legítimo e, es decir, para cualquier 𝑒 tal que 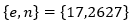, y que su 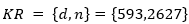, el cual muestra que este módulo conduce a un sistema criptográfico RSA completamente inseguro. Veamos como sucede esto, como 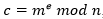, es suficiente demostrar que , para todos los e legítimos, es decir, para todos los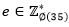 
9 .Tenemos que , esta afirmación lo comprobamos con la Tabla 4.
Esto se podría generalizar para montar el ataque cíclico al descifrar un texto cifrado c, con solo conocer la clave pública correspondiente {n, e}, esto sucede porque el cifrado RSA es una permutación de mensajes en el espacio {1,2,3, …n-1}. Entonces existe un entero positivo k tal que 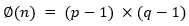; en este caso también existe , que nos lleva a encontrar el texto nativo m, esta particularidad lleva al ataque cíclico que se formula con el siguiente algoritmo 2, Tabla 5.
Implementación del cifrado y descrifado RSA
Mostramos en la Tabla 6, el código en Python de la generación de la clave pública y privada tomada de (Sweigart, 2013), observar que la clave pública y privada se encuentran en los ficheros Clave_pubkey.txt y Clave_privkey.txt respectivamente, y que el tamaño de la clave es de 1024 bits, además del cálculo de los valores de p, q, d y e.
Mostramos en la Tabla 7, el código de cifrado y descifrado del texto nativo para un tamaño de bloque de 128 bytes en el lenguaje Python, tomada de (Sweigart, 2013), observar que el texto cifrado se encuentra en el fichero archivo_cifrado.txt.
Ejecución del código rsaCifradoDescifrado.py, y para el descifrado modificamos el código de la tabla 7 por mode="decrypt" según corresponda, la ejecución del cifrado y descifrado se visualiza en la Tabla 8.
RESULTADOS Y DISCUSIÓN
De hecho, el mayor progreso que se ha hecho en la factorización en los últimos tiempos probablemente no habría sucedido si no fuera por el algoritmo RSA. A pesar de que la factorización se ha vuelto más fácil de lo que los diseñadores de RSA habían asumido, factorizar módulos de RSA más allá de cierto tamaño todavía está fuera del alcance. La longitud exacta que debe tener el módulo RSA es un tema de mucha discusión, muchas aplicaciones RSA usan una longitud de 1024 bits por defecto. Hoy se cree que podría ser posible factorizar números de 1024 bits dentro de un periodo de unos 10 a 15 años o tal vez menos, y más aún las organizaciones de inteligencia podrían ser capaces de hacer esto posible incluso antes. Por lo tanto, se recomienda elegir los parámetros RSA en el rango de 2048 a 4096 bits para seguridad a largo plazo, si el valor del exponente es alto, entonces la seguridad del algoritmo RSA también es alta (Saranya et al., 2014).
Los Laboratorios RSA actualmente recomienda tamaños de clave de 1024 bits para uso corporativo y 2048 bits para claves extremadamente valiosas como el par de claves raíz utilizado por una autoridad de certificación, además varios estándares recientes especifican un mínimo de 1024 bits para uso corporativo. Es posible también que se cifre información menos valiosa utilizando una clave de 768 bits, ya que dicha clave sigue siendo segura y está fuera del alcance de todos los algoritmos de ruptura conocidos (Dooley, 2018).
La probabilidad de elegir aleatoriamente el mismo p o q repetidamente es muy improbable, en la programación de computadoras, la buena aleatoriedad proviene de algoritmos conocidos como generadores deterministas de bits aleatorios (DRBG). Los DRBG requieren datos de entrada denominados semillas de entropía, que provienen de una fuente (o fuentes) que generan eventos que no presentan ningún signo de similitud o previsibilidad de patrones. Si la fuente cumple con estos criterios simples, se sabe que es una buena fuente de entropía. Los algoritmos DRGB son revisados a fondo por investigadores de seguridad, matemáticos, universidades, así como por el Instituto Nacional de Estándares y Tecnología (NIST). Una buena fuente de entropía es aquella que pasará la prueba de evaluación de entropía del NIST, el cual creo un conjunto de pruebas estadísticas que ejecutará en su fuente de entropía. El código fuente de esta herramienta está disponible en https://github.com/usnistgov/SP800-90B_EntropyAssessment. Si una fuente pasa la prueba, esta se considera una buena para la generación segura de aleatoriedad, el cual se puede utilizar para generar claves de cifrado, o seleccionar aleatoriamente los valores de 𝑝 y 𝑞 (Labs, 2020).
Los sistemas de cifrado que implementan criptografía de clave pública tienen aproximadamente la misma seguridad como el de los sistemas de claves simétricas con longitudes equivalentes de clave de aproximadamente un tercio de longitud de la clave RSA. Los sistemas de cifrado de clave pública son sistemas lentos, en algunos casos muy lentos, mientras que los sistemas simétricos como DES y AES usan operaciones informáticas muy simples como desplazamiento de bits y/o operaciones lógicas como el or exclusivo. Hasta la fecha todos los sistemas de clave pública desarrollados requieren operaciones matemáticas muy complicadas para cifrado, estas funciones matemáticas requieren mucho más tiempo de procesamiento de la CPU, que las simples operaciones requeridas para sistemas simétricos, es por eso que los sistemas de clave pública tienen limitaciones principalmente para el papel para el que fueron concebidos por primera vez, que es el de resolver el intercambio de claves.
CONCLUSIONES
La seguridad del RSA no lo sabemos, tal vez hay un algoritmo de tiempo polinómico que pueda factorizar números o resolver el problema del logaritmo discreto, no conocemos ninguna forma de romper RSA que no sea factorizando el módulo, pero una vez más, nadie sabe si existen otros métodos que podrían romper el RSA que no sean equivalentes a la factorización.
Para evitar el ataque de la factorización, el módulo debe ser lo suficientemente grande, es decir se debe trabajar con módulos de 1024 bits o más, además de tener en cuenta que cuando se usa RSA, debemos rellenar primero el mensaje para evitar el ataque basado en la maleabilidad del RSA, y para evitar o bloquear la deducción práctica de la clave privada d mediante el ataque cíclico, debemos de utilizar primos seguros en el diseño de las claves.
La seguridad del algoritmo RSA radica en dos áreas, primero, si bien es fácil calcular n=p x q, es muy difícil hacer lo contrario; es decir obtener p y q, dado n, y segundo, es extremadamente costoso computacionalmente encontrar los factores primos de un número compuesto grande, el cual es el eje de seguridad del RSA. Los dos números primos p y q deben ser números primos muy grandes, suficientemente grandes para que sus representaciones binarias de cada uno sean alrededor de 500 bits o más. Esto conducirá a un producto binario de alrededor 1000 bits, a medida que las computadoras se vuelven cada vez más rápidas, se necesitará que las cantidades de bits para n=p x q también tengan que crecer.
Sobre los productos comerciales de seguridad del RSA, nosotros debemos verificar qué fuentes de entropía utilizan, siempre es una buena pregunta que debemos hacernos. Los productos del RSA Security usan una variedad de módulos criptográficos, que incluyen, entre otros a, RSA BSAFE ® Crypto-C Micro Edition (Crypto-C ME)10 que tiene su fuente de entropía probada contra las pruebas de NIST, y RSA BSAFE ® Crypto-J (Crypto-J )11, que se basa en la máquina virtual de Java en la que se ejecuta la entropía. RSA BSAFE ®, es una biblioteca de criptografía validada por el FIPS 140-212, disponible en C y Java, ofrecida por RSA Security.
