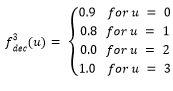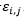Servicios personalizados
Español (pdf)
Articulo en XML
Referencias del artículo
Enviar articulo por email
Citado por SciELO 
Similares en
SciELO 
Permalink
INTRODUCCIÓN
En los últimos años una nueva familia de algoritmos evolutivos conocidos como Algoritmos de Estimación de Distribuciones (EDA, del inglés, Estimation of Distribution Algorithm) (Mühlenbein, y otros, 1999; Larrañaga y otros, 2002) ha despertado gran interés en la comunidad científica relacionada con la optimización, la computación evolutiva y los modelos probabilísticos. Estos algoritmos surgieron como una alternativa a los algoritmos genéticos. Los EDA están motivados por la necesidad de identificar las interrelaciones entre las variables (Madera, y otros, 2018). Las sucesivas generaciones de individuos se crean a partir de la estimación de la distribución de probabilidad observada en la población actual. Consecuentemente, el principal rasgo que distingue a los EDA de otros algoritmos evolutivos es que aprenden las interacciones entre las variables del problema (Tsagris, 2020; Dai, y otros, 2020).
Los EDA centran su funcionamiento en la construcción y simulación de distribuciones de probabilidad. La complejidad de las distribuciones está asociada con la capacidad del modelo utilizado para expresar las relaciones de dependencias que existen entre las variables del problema. A medida que aumenta la complejidad de la estructura, el EDA necesitará mayor cantidad de individuos para hacer una correcta estimación del modelo aumentando directamente el costo computacional del algoritmo.
Reducir el costo del proceso de búsqueda es una cuestión crítica en EDA. Usualmente este costo se relaciona con el número de evaluaciones de la función objetivo (costo evaluativo) y el tiempo de ejecución del algoritmo (costo en tiempo). Una reducción combinada del costo evaluativo y el costo en tiempo permitirá abordar clases de problemas de complejidad creciente que aparecen tanto en la academia como en el mundo real.
En este artículo se propone la utilización de un EDA para la solución de problemas de optimización discretos y en la predicción de la estructura terciaria de proteínas con un modelo simplificado (Santana, y otros, 2008; Bergasa-Caceres, y otros, 2020; Brower, y otros, 2020; Mazidi, y otros, 2020; Fefelova y otros, 2020; Zarges, 2020). S demuestra la utilidad de los EDA basados en restricciones para resolver estos problemas (Mühlenbein, y otros, 1999a; Mühlenbein, y otros, 2006; Krejca, y otros, 2020), resultando en un algoritmo práctico que permite no acudir a modelos de EDA más complejos como los Markovianos (Tsagris, 2020; Dai, y otros, 2020). Los resultados experimentales muestran que este método es capaz de obtener resultados similares a otros algoritmos del estado del arte a un menor costo.
La estructura del artículo es la siguiente: en la próxima sección se presenta la metodología computacional propuesta. En la misma se propone un nuevo algoritmo EDA basado en restricciones. Posteriormente se presentan los problemas de optimización propuestos para la validación y comparación de los algoritmos. Una vez definida la base para la experimentación se procede al análisis de los resultados y discusión. Por último, se presentan las conclusiones y trabajo futuro de la investigación.
METODOLOGÍA COMPUTACIONAL
Los EDA fueron introducidos por primera vez en el campo de la computación evolutiva en (Mühlenbein, y otros, 1999; Larrañaga, y otros, 2002), concebidos para sustituir los operadores de cruzamiento y mutación del algoritmo genético (GA, del inglés, Genetic Algorithm) recientes trabajos en esta área han demostrado la utilidad del operador de mutación en este tipo de algoritmo, interpretado como un operador de variación probabilística (Ochoa, y otros, 2006). De forma general los EDA utilizan una población seleccionada para estimar la distribución de probabilidad y a partir de esta se generan los puntos que formarán la nueva población. Así, las relaciones de dependencia entre las variables quedan especificadas de forma explícita a través del modelo probabilístico del conjunto seleccionado.
El algoritmo EDA es teórico, producto a que el cálculo de todos los parámetros necesarios para especificar la distribución de probabilidad es intratable. Producto a esta dificultad es que surge el algoritmo con distribución factorizada (FDA, del inglés, Factorized Distribution Algorithm) (Mühlenbein, y otros, 1999; Mühlenbein, y otros, 2006; Krejca, y otros, 2020) con el objetivo de hacer de los EDA algoritmos tratables. En la literatura especializada varios autores se refieren a EDA como la clase de los algoritmos evolutivos basados en estimación y simulación de distribuciones.
En este artículo se propone la utilización del algoritmo 𝐶𝐵??𝐷𝐴 𝑇𝑃𝐷𝐴 (del inglés, Constraint Based EDA) (Madera, 2009; Madera, y Otros, 2018) basado en el algoritmo de análisis de dependencias de tres fases (TPDA, del inglés, Three - Phase Dependency Analysis algorithm) (Madera, 2009). El TPDA utiliza un esquema híbrido para la construcción de la red Bayesiana (distribución de búsqueda del EDA). En una primera etapa construye un esqueleto a través de pruebas de independencias, luego el esqueleto es orientado utilizando un procedimiento de optimización de métricas. La utilización de este algoritmo se justifica por dos razones fundamentales: (1) por sus propiedades numéricas, dónde supera a otros algoritmos del estado del arte y (2) por la posibilidad de encontrar dependencias entre las variables, algo común en la predicción de la estructura terciaria de proteínas.
Algoritmo de estimación de distribuciones basado en restricciones
Los EDA han sido motivados por la necesidad de identificar las dependencias entre las variables, una cuestión clave para resolver problemas complejos. Por lo tanto, la principal característica que distingue a los EDA de otros algoritmos evolutivos (EA, del inglés, Evolutionary Algorithms) es que aprenden las interacciones entre las variables del problema. Los EDA se clasifican según el modelo de aprendizaje utilizado y van desde los que asumen total independencia de las variables, hasta los que toman en cuenta interacciones por pares; algunas familias de EDA también consideran modelos generales no restringidos de interacción entre variables.
El presente enfoque aprovecha la detección de independencias para construir la red bayesiana (Madera, y otros, 2018; Brownlee, y otros, 2015). Formalmente, se puede tener una red bayesiana sobre el conjunto de variables aleatorias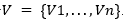 
.
La factorización de la distribución de probabilidad conjunta puede expresarse como:
(1)
donde, Pai es el conjunto de padres de Vi (es decir, existe un arco de cada nodo en Pai a Vi).
Existen dos métodos diferentes para aprender la estructura probabilística de un conjunto de datos. El primer método concibe la utilización de un procedimiento de puntuación + búsqueda (Madera, 2009; Madera, y otros, 2018). Estos métodos definen una métrica (función de costo) que mide la idoneidad de cada red bayesiana candidata para una base de datos. El otro enfoque se sustenta sobre pruebas de independencia para obtener una lista de relaciones en forma de aristas. Estos algoritmos construyen la estructura gráfica respetando, en la medida de lo posible, las relaciones presentes de la lista (Brownlee, y otros, 2015; Madera y Ochoa, 2018).
El algoritmo propuesto en este artículo utiliza un enfoque híbrido. En una primera fase, se construye un esqueleto a partir de pruebas de independencia, posteriormente se orientan las aristas con la aplicación de un procedimiento de puntuación + búsqueda (Madera, 2009; Madera, y otros, 2018).
El algoritmo CBEDATPDA
El procedimiento del CBEDATPDA (ver Algoritmo 1) utiliza el algoritmo TPDA para el aprendizaje de redes Bayesianas (Cheng, y otros, 2002). Este algoritmo permite extraer las dependencias entre las variables de los individuos que forman el conjunto seleccionado. La propuesta original se modificó para permitir su aplicación en el contexto de los EDA. Se propone un nuevo método para orientar las aristas basado en un procedimiento de puntuación + búsqueda. A los lectores interesados se les recomienda revisar el artículo original de Cheng y las referencias citadas para profundizar en los detalles del algoritmo TPDA.
Algoritmo 1 - Propuesta del algoritmo CBEDATPDA.
En este artículo se toman en cuenta cuatro variantes del algoritmo CBEDATPDA:
Algoritmo CBEDATPDA: utiliza la implementación original del algoritmo 𝑇𝐷𝑃𝐴 orientando el esqueleto mediante un procedimiento de puntuación + búsqueda.
CBEDATPDA-RO: Construye el esqueleto de la red Bayesiana de la misma forma que el algoritmo TPDA original pero las aristas son orientas de forma aleatoria.
CBEDATPDA-PT: Restringe la estructura de la red Bayesiana aprendida a un poliárbol (existe un solo camino entre cualquier par de nodos).
CBEDATPDA-k2: Restringe el número de nodos adyacentes de cualquier nodo a dos.
Problemas
Para retar a los CBEDA propuestos se utilizan las funciones decepcionantes que se descomponen aditivamente con representación binaria y no-binaria (Goldberg, y otros, 1992; Santana, y otros, 2002). También se estudia el comportamiento de los algoritmos en un problema de la Bioinformática, la predicción de estructuras de proteíanas en modelos simplificados (Bergasa-Caceres, y otros, 2020; Brower, y otros, 2020; Mazidi, y otros, 2020; Fefelova, y otros, y otros, 2020; Zarges, 2020; Santana, y otros, 2008).
Función Fdeceptive3
La función Fdeceptive3 (Goldberg, y otros, 1992; Santana, y otros, 2002) se define de la siguiente manera:
(2)
Donde,
(3)
El objetivo es maximizar la función Fdeceptive3 y el óptimo global se encuentra en el punto (1,1,…,1).
Función decepcionante con representación entera
El análisis del comportamiento de los EDA se ha centrado en el estudio de problemas binarios. Sin embargo, para estudiar la robustez de los EDA y su posible aplicación a problemas reales se hace necesario el estudio de problemas no-binarios (representación entera). Con este fin, se utilizará una función decepcionante definida para problemas con representación entera (Santana, y otros, 2002).
La función general para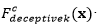 
de orden 𝑘 está formada por una función aditiva compuesta por la función 
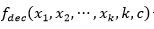evaluada en subcadenas de tamaño k y cardinalidad c, es decir, 
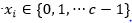. Esta función es una generalización de la función Fdeceptive3 para variables con representación entera.
La función queda definida de la siguiente manera:
(4)
Donde, se define como:
(5)
El problema de la predicción de la estructura de proteínas
Las proteínas son cadenas o secuencias formadas por la combinación de 20 aminoácidos enlazados mediante enlaces peptídicos. En el espacio, dicha cadena adopta una estructura tridimensional, la que determina la funcionalidad biológica de la proteína. Esta estructura tiene cavidades y salientes que permiten el acoplamiento con otras proteínas para formar estructuras más complejas, o para bloquear el funcionamiento de otras.
Estructuralmente, las proteínas pueden analizarse a diferentes escalas. Se denomina estructura primaria de una proteína, a la secuencia de aminoácidos que la componen. Estos aminoácidos se agrupan en estructuras llamadas α hélices, laminas β y loops, las cuales reciben el nombre de estructuras secundarias. Estas subestructuras se pliegan o “doblan” en el espacio tridimensional hasta alcanzar una configuración que se conoce como estructura terciaria o estado nativo. Es esta estructura tridimensional la que determina la funcionalidad biológica de la proteína (Branden, y otros, 1998).
Resulta aceptado que uno de los elementos que más influye en la determinación de esta estructura, es el llamado efecto hidrofóbico. Los aminoácidos pueden clasificarse en hidrofílicos o hidrofóbicos según sea su comportamiento en un medio acuoso. En el proceso de plegado los aminoácidos hidrofóbicos tienden a agruparse en el centro de la molécula formando una especie de coraza interna, mientras que los hidrofílicos tienden a quedar expuestos al solvente. Se puede definir el problema de la predicción de la estructura de una proteína como la búsqueda, a partir de la secuencia de aminoácidos, de la estructura tridimensional correspondiente.
Un modelo para PSP es relevante si refleja alguna de las propiedades del proceso de formación de estructura en el sistema real. De acuerdo con la hipótesis termodinámica, el estado nativo de una proteína se corresponde con el estado de mínima energía libre y por eso los modelos basados en energía especifican una función de “costo” que asigna un valor de energía libre a cada estructura válida. Se asume que la estructura terciaria de la proteína se corresponderá entonces, con aquella conformación que minimice la función de energía.
Dentro de este tipo de modelos basados en energía se destacan los modelos basados en retículos. Donde, cada vértice del retículo es ocupado por un aminoácido de la cadena y aminoácidos consecutivos en la secuencia se ubican en posiciones adyacentes del retículo.
Los modelos en retículos utilizan las coordenadas internas para modelar las estructuras terciarias de las proteínas, dada la posición del aminoácido i, existen 𝛿 valores para representar la posición del i + 1dependiendo del retículo utilizado (bidimensional, tridimensional o de diamante).
El modelo más simple de PSP en retículos, llamado modelo de Dill (Dill, 1985) solo considera dos tipos de aminoácidos, donde cada tipo representa si es hidrofóbico (representado con una H) o hidrofílico (representado con una P). Una proteína entonces, se modela como secuencia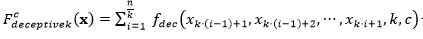. En la Figura 1 se muestra un ejemplo de configuración de una proteína en el modelo HP.
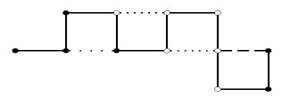
Fig. 1 Posible configuración para la secuencia 𝐻𝐻𝐻𝑃𝐻𝑃𝑃𝑃𝑃𝑃𝐻 para el modelo HP en un retículo bidimensional. La configuración muestra un contacto 𝐻𝐻, uno 𝐻𝑃 y dos 𝑃𝑃.
La función de energía utilizada, solo tiene en cuenta las interacciones entre aminoácidos que sean adyacentes en el retículo, pero no consecutivos en la secuencia (vecinos topológicos). Cada interacción de este tipo se denomina bond o contacto. Dada una secuencia con n aminoácidos,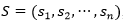 
, con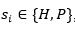
, un plegado para 
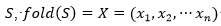dispuesto en un retículo L, y una matriz de interacción (si, sj), una función de energía posible es:
(6)
Donde son adyacentes en el retículo y no consecutivos en la cadena y 0 en caso contrario. El término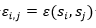 
es el valor de la fila i, columna j en la matriz de interacción E . En la Figura 2 se muestran dos matrices de interacción posibles.
Con estos elementos se establece que resolver PSP en este modelo es equivalente a minimizar la función de energía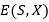 
(ecuación 6).
Las estructuras en estos modelos se representan a través del sistema de coordenadas internas, de las cuales aparecen dos variaciones: la codificación mediante coordenadas absolutas y coordenadas relativas, en este artículo de utiliza la última codificación.
RESULTADOS Y DISCUSIÓN
En esta sección se analiza el comportamiento del algoritmo cuando se varía la cardinalidad de las variables (conjunto de posibles valores que puede tomar cada variable). Para tal propósito se utiliza la función F deceptive3 c, donde c ∈ {2,3,4,5,6,7}. La metodología utilizada fue encontrar el tamaño de población crítica M para el algoritmo CBEDATPDA y posteriormente ejecutar el resto de los algoritmos (CBEDATPDA-RO, CBEDATPDA-PT, CBEDATPDA-k2) con el tamaño de población encontrado. Para obtener el tamaño de población crítica se inicia con una población de 1000 individividuos y si el porciento de éxito es inferior al 95% se incrementa el tamaño de población en 1000 individuos y así hasta lograr el porciento de convergencia deseado. La excepción es la función Fdeceptive3 que por ser la de menos complejidad determinamos su población crítica a partir de un incremento de 100 individuos en cada fallo.
Para cada función y algoritmo se ejecutaron 50 corridas independientes.
El análisis de la Tabla 1 muestra claramente una superioridad del algoritmo CBEDATPDA en cuanto al porciento de éxitos, evidenciándose fluctuaciones en el resto de las propuestas. Esto es un resultado esperado pues los algoritmos CBEDATPDA-RO, CBEDATPDA-PT, CBEDATPDA-k2 son variantes restringidas del original CBEDATPDA.
Otro resultado interesante es el comportamiento en cuanto al número de evaluaciones del CBEDATPDA-RO en los problemas con cardinalidad 2, 3 y 4, superado por el CBEDATPDA para las cardinalidades 5, 6, y 7. El peor rendimiento lo exhibe el CBEDATPDA-PT, cuya estructura no permite obtener mejores resultados en cuanto al número de evaluaciones. Este algoritmo tendrá mejor o igual comportamiento que el CBEDATPDA (debe ser capaz de aprender la estructura correcta) si las funciones estudiadas tuvieran una estructura probabilística en forma de poliárbol (Soto, 2003; Ochoa, y otros, 2006). Por último, queda demostrado que el aumento de la cardinalidad de las variables del problema es fuente de complejidad adicional como lo pueden ser el aumento de la cantidad de variables, si son decepcionantes o no, así como tener entropía univariada (o de orden superior) alta (Ochoa y Soto, 2006). El aumento de la complejidad queda reflejado en el aumento del tamaño de la población crítica a medida que aumenta la cardinalidad, así como el aumento en el número de evaluaciones realizada por el algoritmo.
Escalabilidad de los CBEDA para Fdeceptive3
En esta sección se hace un estudio de escalabilidad numérica y física (tiempo de ejecución) de los diferentes CBEDA para la función Fdeceptive3. La tabla muestra los resultados de escalabilidad, a partir del incremento en el número de variables desde 15 hasta 90. Para todas las configuraciones, excepto la de 15 variables, el CBEDATPDA-RO obtiene el mejor rendimiento numérico (menor número de evaluaciones) y en tres de las configuraciones también obtiene los menores tiempos de ejecución. Con respecto al tiempo de ejecución, el CBEDATPDA-RO no realiza optimización de métrica por lo que se ahorra ese tiempo que es obligatorio para las demás variantes y que evidentemente es mayor que la generación de una permutación aleatoria de las variables.Tabla 2
Resultados para el problema de la predicción de estructuras de proteínas
En esta sección se muestran los resultados de la aplicación del CBEDATPDA en la solución del problema de la predicción de estructuras de proteínas y su comparación con otros algoritmos del estado del arte de la computación evolutiva.
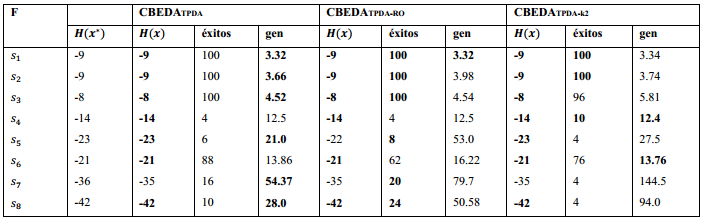
La Tabla 3 muestras las instancias del modelo HP utilizadas en los experimentos, 𝐻( x ∗ ) representa la mejor solución conocida para la secuencia. PSP se ha estudiado, utilizando las secuencias descritas.
El primer experimento consiste en encontrar el óptimo para las secuencias de la Tabla 3 con la aplicación de tres variantes del CBEDATPDA. La primera es el algoritmo CBEDATPDA clásico, la segunda realiza una orientación aleatoria del esqueleto (CBEDATPDA−RO) y la tercera restringe el número de nodos adyacentes a dos (CBEDATPDA−k2).
La metodología empleada es similar a la utilizada en el estudio de otros EDA (Cotta, 2003). Todos los algoritmos tienen un tamaño de población de 5000 individuos, ejecutándose un máximo de 5000 generaciones. El truncamiento es de 0.1 con la aplicación del mejor elitismo (toda la población seleccionada pasa directamente a la próxima generación). La Tabla 4 muestra los resultados obtenidos en los experimentos, donde la columna éxitos es el porciento de veces que se encontró la mejor solución en 50 corridas independientes y gen representa la generación media donde se encontró la mejor solución. Los mejores resultados de cada parámetro medido son destacados en negritas.
Los resultados muestran como todas las variantes del CBEDATPDA encuentran la mejor solución para las secuencias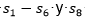 
excepto el CBEDATPDA-RO en la secuencia S5 que obtiene una solución sub-óptima. En el caso de la secuencia S7 todos los algoritmos obtienen una solución sub-óptima, en (Cotta, 2003) se muestra empíricamente como esta instancia es decepcionante lo que aumenta su complejidad. Al igual que en (Cotta, 2003) los resultados para los CBEDA son promisorios debido a que no se utilizan técnicas de optimización local ni los parámetros se han refinado para cada instancia.
El siguiente experimento tiene como motivación la siguiente pregunta: ¿Es necesario acudir a modelos de aprendizaje más complejos como las redes de Markov para la solución de PSP tridimensional con EDA? Para dar respuesta a la pregunta seguimos un experimento similar al utilizado por Santana y otros (Santana, y otros, 2008), configurando el CBEDATPDA con un tamaño de población de 5000 individuos y un máximo de 1000 generaciones. El truncamiento es de 0.1 con la estrategia del mejor elitismo al igual que en los experimentos para retículos en dos dimensiones. La comparación se realiza entre el GA híbrido (Cutello, y otros, 2007), el 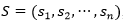(el subíndice dos significa que cada nodo puede tener a lo sumo dos nodos adyacentes) y el CBEDATPDA.
Los resultados se muestran en la Tabla 5. Se puede apreciar que el CBEDATPDA supera al GA híbrido y al 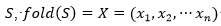en el promedio del óptimo obtenido para las instancias de la s1 -s4 y para la instancia s6. En el caso de las instancias s5 y s7, ambos EDA obtienen el mismo valor, aunque el 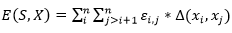supera en el promedio del óptimo al CBEDATPDA. Para la instancia s8 el 
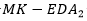mejora al GA híbrido y al CBEDATPDA, tanto en el óptimo encontrado como en el promedio. Una observación importante es que los EDA superaron siempre los resultados obtenidos por el GA híbrido, aun cuando este último utiliza técnicas de optimización local para la resolución del problema PSP.
Cómo respuesta a la pregunta planteada podemos decir que no es necesario acudir a modelos complejos de EDA para la solución de PSP en las secuencias estudiadas. Los modelos Bayesianos obtienen resultados similares a los modelos Markovianos con la ventaja de no estar restringida la estructura (en el 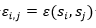cada nodo puede tener a lo sumo dos nodos adyacentes). En una futura investigación se puede comprobar si la inclusión de un optimizador local mejora las soluciones obtenidas con el CBEDATPDA.
CONCLUSIONES
En este artículo se propuso la utilización de algoritmos EDA para resolver problemas de dominio entero, específicamente la función Fdeceptive y el problema de la predicción de la estructura terciaria de proteínas. Se utilizó el algoritmo CBEDATPDA por su posibilidad de detectar dependencias entre las variables durante la optimización. Los resultados experimentales demostraron, que las soluciones encontradas son comparables con los algoritmos del estado del arte, incluso para algunas instancias los superan. En el caso del problema PSP dos dimensiones el algoritmo CBEDATPDA, sin modificaciones, encuentra mejores soluciones que otras variantes del mismo. Para tres dimensiones en PSP se demuestra que acudir a modelos más complejos (
) de EDA resulta innecesario.
Como trabajo futuro se recomienda incorporar al CBEDATPDA un optimizador local para mejorar el rendimiento del mismo, así como un reparador de secuencias con cualidades superiores. Una mejora posible al algoritmo propuesta es estructurar la población espacialmente, utilizando algoritmos celulares y distribuidos. Se propone extender los experimentos a secuencias más complejas, así como su comparación con otros algoritmos fuera del campo de los EDA y los algoritmos genéticos.
