Servicios personalizados
Español (pdf)
Articulo en XML
Referencias del artículo
Enviar articulo por email
Citado por SciELO 
Similares en
SciELO 
Permalink
Introducción
En la actualidad el volumen de los datos generados por sensores, Internet, dispositivos de localización, telefonía y muchos otros, está en constante aumento. El tamaño de estos datos es potencialmente infinito, debido a su constante generación y así, es necesario procesarlos con recursos limitados de cómputo. Para este procesamiento es factible el uso de técnicas de minería de flujos de datos. En las tareas de clasificación, un flujo de datos es comúnmente definido como una secuencia muy grande (potencialmente infinita) de pares que se van adquiriendo a lo largo del tiempo. Estos pares, llamados instancias o ejemplos, están compuestos por un conjunto de atributos y una etiqueta de clase. Debido a la dimensión temporal de los datos (estos son adquiridos en el tiempo) y la dinámica de muchas situaciones reales, la distribución de probabilidad que regula a los datos (también llamada concepto) puede cambiar con el tiempo, un problema conocido comúnmente como cambio de concepto. Consecuentemente, los algoritmos de aprendizaje para la minería de flujos de datos deben ser actualizados con respecto a los conceptos más recientes (Gama et al. 2014).
Los métodos de ensambles de clasificadores (o combinación de clasificadores) han recibido en los últimos tiempos gran atención para el modelado y la clasificación de flujos de datos no estacionarios (Blanco et al. 2010; Verdecia-Cabrera et al. 2019). El objetivo de estos métodos es que tengan mejor rendimiento que los clasificadores individuales (también llamados clasificadores base (Kuncheva 2004; Verdecia-Cabrera et al. 2018). Para manipular cambios de concepto, utilizan medidas de rendimiento para monitorizar la consistencia del ensamble en relación con los nuevos datos. Variaciones significativas en los valores de rendimiento se interpretan como un cambio de concepto y los métodos de ensamble eliminan, reactivan o añaden nuevos clasificadores base dinámicamente en respuesta a estas variaciones.
En el aprendizaje en línea, los métodos para combinar las predicciones de los clasificadores base se han centrado en el voto ponderado, que consiste en asignarle a cada clasificador base del ensamble un peso proporcional a su precisión estimada (Littlestone y Warmuth 1994). Así, en las tareas de predicción, el ensamble realiza el voto final ponderando los votos de los clasificadores bases en correspondencia con los pesos estimados. Sin embargo, la relación subyacente entre las predicciones de los clasificadores bases y de las etiquetas de clases puede ser más compleja que una combinación lineal de las predicciones. Por ejemplo, el uso de un meta-clasificador es una opción factible; en este caso, las predicciones de los clasificadores base sirven como entrada para un meta-clasificador y la salida del meta-clasificador es la clase final predicha por el ensamble.
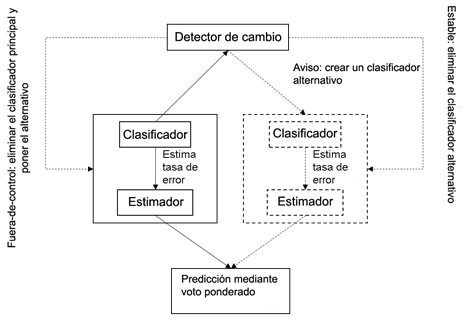
Este artículo presenta un nuevo método de ensamble que aplica el esquema de FASE (Fast Adaptive Stacking of Ensembles) (Frías-Blanco et al. 2016; Verdecia-Cabrera, Blanco y Carvalho 2018) al algoritmo Boosting (Oza y Russell 2001). FASE utiliza HDDM (Hoeffding Drift Detection Method) (Frias-Blanco et al. 2015) como detector de cambios de concepto y estimador de error. Cuando se detecta un cambio, se elimina el peor clasificador del ensamble y se agrega uno nuevo. FASE está compuesto por clasificadores adaptativos en los dos niveles (ambos clasificadores el base y el meta son adaptativos). Cada clasificador adaptativo usa HDDM, que monitoriza su tasa de error con el objetivo de emitir tres señales diferentes de cambio durante el proceso de aprendizaje. HDDM emite la señal en-control cuando el concepto actual permanece estable, alerta cuando es probable que se aproxime un cambio, y fuera-de-control cuando se detecta el cambio. En FASE, cada clasificador adaptativo usa un solo clasificador en los conceptos estables. Cuando el nivel de alerta es alcanzado, el clasificador adaptativo entrena un clasificador alternativo que reemplaza al principal si después del nivel de alerta ocurre un cambio. Los clasificadores adaptativos pueden de esta forma tener a lo sumo dos clasificadores (el clasificador principal y el alternativo), las predicciones de estos clasificadores son combinadas mediante el voto ponderado. Por lo tanto, FASE-Boost puede ser visto como un ensamble de clasificadores de 3 niveles, donde cada nivel es capaz de manipular cambios de concepto de forma explícita.
METODOLOGÍA COMPUTACIONAL
Apilado de Ensamble de Clasificadores
El nuevo algoritmo, llamado FASE-Boost es un ensamble de clasificadores que utiliza un meta-clasificador para combinar las predicciones de los clasificadores bases del ensamble. FASE-Boost Solo recibe como parámetros el nivel de confianza del detector de cambios y el número de clasificadores base. Por tanto, para ajustar estos parámetros no se necesita conocer previamente los tipos de cambios o conceptos objetivo. La sección “Clasificadores adaptativos” presenta el diseño de los clasificadores adaptativos. La sección “Combinación de la predicción de los clasificadores adaptativos” describe el proceso del meta-aprendizaje, es decir como se construyen las instancias para entrenar el clasificador del nivel meta.
Clasificadores adaptativos
Los modelos de aprendizaje comúnmente aumentan su tasa de error de clasificación cuando ocurre un cambio de concepto, ya que en estos casos el modelo de aprendizaje inducido no está acorde a los datos más recientes. En FASE-Boost, los clasificadores adaptativos estiman las tasas de error con un enfoque predictivo secuencial (test-then-train) (Gama, Sebastião y Rodrigues 2013). Así, a la llegada de cada ejemplo de entrenamiento, el modelo de aprendizaje hace una predicción basada en sus valores de atributo, entonces este ejemplo se pone a disposición el algoritmo para continuar con su aprendizaje. Como algunos de los enfoques anteriores, FASE-Boost utiliza la función de pérdida 0-1 entre la etiqueta de clase predicha y el valor real de la misma para la estimación del error.
La Figura 1 muestra el esquema general seguido en los clasificadores adaptativos. Este mecanismo se basa en la propuesta de (Gama et al. 2004) y otros enfoques relacionados (Baena et al. 2006; Frias-Blanco et al. 2015). A diferencia de estos enfoques, FASE-Boost utiliza un voto ponderado para combinar las predicciones del modelo principal y los modelos alternativos. Los pesos son inversamente proporcionales a las tasas de error, las cuales son estimadas por los detectores de cambio correspondientes.
Combinación de la predicción de los clasificadores adaptativos
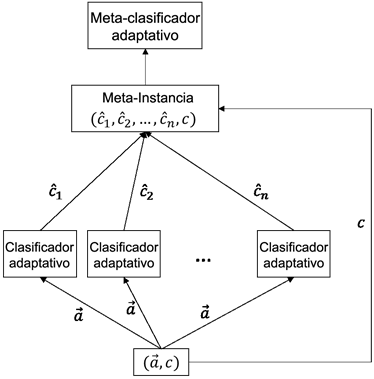
El meta-clasificador de FASE-Boost recibe meta-instancias como entrada, donde cada atributo es nominal. FASE (Frías-Blanco et al. 2016) utiliza el enfoque test-then-train (Gama, Sebastião y Rodrigues 2013) para generar meta-instancias (ver la Figura 2). Por lo tanto, para cada instancia original de entrenamiento 
, FASE genera una meta-instancia de entrenamiento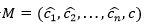 
, donde 
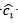son los valores de los atributos y c su etiqueta de clase correspondiente. Cada valor de atributo 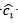de la meta-instancia M corresponde con la predicción del clasificador base i para la instancia I. Para esta meta-instancia M, el valor 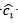es la clase predicha por el clasificador i. La etiqueta de clase de la meta-instancia M es la misma que la de la instancia de entrenamiento original.
El conjunto de clasificadores base puede cambiar con el tiempo, ya que los clasificadores adaptativos pueden alternar clasificadores en respuesta a un cambio de concepto. El detector de cambio que controla la tasa de error del conjunto también puede eliminar los clasificadores adaptativos como clasificadores base. Por lo tanto, el meta-clasificador puede ser afectado por cambios en el concepto objetivo que relaciona las predicciones de los clasificadores base con la etiqueta de clase verdadera de un ejemplo dado. FASE-Boost utiliza un algoritmo de aprendizaje adaptativo como meta-clasificador con el fin de manejar este tipo de cambio de concepto.
Estudio Experimental
Un aspecto importante dentro del aprendizaje automático es la evaluación de los métodos y algoritmos con el objetivo de validar su rendimiento. Al mismo tiempo, este proceso es útil para evaluar la aplicabilidad de los métodos, para detectar puntos que pueden ser mejorados o incluso compararlos con alternativas diferentes. Por estas razones es necesario adaptar los métodos de evaluación cuando se aprende con cambio de concepto. Para analizar el rendimiento de los algoritmos que realizan tareas de clasificación en presencia de cambios de concepto se utilizó la precisión.
Configuración de los algoritmos adaptativos
En este trabajo se compara FASE-Boost con FASE (FASE-Bag) (Frías-Blanco et al. 2016). Además, se utilizaron otros algoritmos implementados en MOA, como OzaBagAdwin y OzaBoostAdwin (Bifet et al. 2009), OzaBag (versión en línea del algoritmo Bagging) (Oza y Russell 2001), OzaBoost (versión en línea del algoritmo Boosting) (Oza y Russell 2001), LeveragingBag (Bifet 2010).
Los algoritmos fueron utilizados con la configuración por defecto en MOA. Como clasificador base se utilizó Naïve Bayes. Para los algoritmos que usan HDDM, el nivel de significación para el cambio fue de 0.001 y para la alerta de 0.005. Se utilizaron 10 clasificadores base en todos los métodos.
Conjuntos de datos
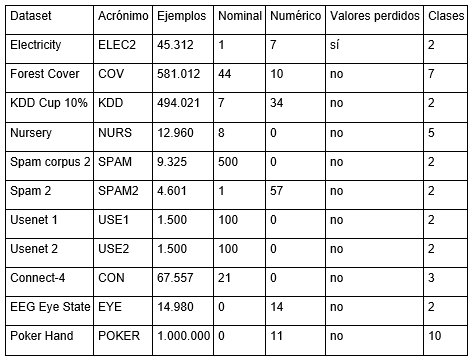
Para realizar el estudio experimental se seleccionaron conjuntos de datos artificiales y reales. Los conjuntos de datos artificiales seleccionados se encuentran disponibles en MOA. En la Tabla 1 se muestran las características principales de los conjuntos artificiales seleccionados. Además, en la Tabla 2 se muestran las características principales de los conjuntos de datos reales seleccionados.
RESULTADOS Y DISCUSIÓN
Experimentos con datos artificiales
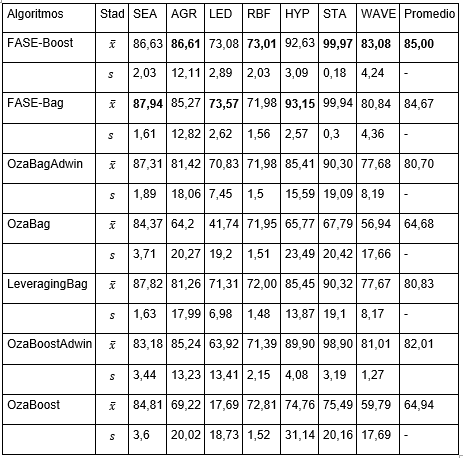
La Tabla 3 muestra el rendimiento de los algoritmos frente a cambios de conceptos abruptos. Con cada generador se simularon 10 cambios de concepto cada 25.000 instancias. El rendimiento de los algoritmos se resume en términos de la media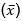 
y la desviación estándar (s) para la precisión. Los mejores valores de precisión se muestran en negritas. Como se puede observar los algoritmos FASE-Boost y FASE-Bag obtienen los mejores resultados.
Experimentos con datos reales
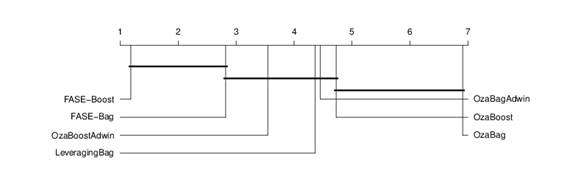
En la Tabla 4 se muestran los resultados obtenidos por los algoritmos usando como clasificadore base Naïve Bayes. Nuevamente se puede comprobar que el algoritmo propuesto es competitivo en cuanto a precisión. Adicionalmente, para comprobar diferencias significativas entre los algoritmos se realizaron pruebas estadísticas siguiendo la metodología propuesta por (Demšar 2006) y (García y Herrera 2008) para comparar varios clasificadores sobre varios conjuntos de datos. En la Figura 3 se puede apreciar que FASE-Boost es significativamente mejor que OzaBagAdwin, OzaBag, LeveragingBag, OzaBoostAdwin y OzaBoost.
Tabla 4 Rendimiento de los algoritmos basados en Bagging sobre las bases reales y como clasificador base Naïve Bayes.
Conclusiones
En este artículo se ha presentado un nuevo algoritmo llamado FASE-Boost. FASE agrega mejoras a los algoritmos basados en Bagging y Boosting, como es el uso de clasificadores adaptativos como clasificadores base y el uso de estos como meta-clasificadores. FASE-Boost procesa los datos de entrada con complejidad temporal y espacial constante, y solo procesan cada ejemplo de entrenamiento una vez. Recibe como parámetros el nivel de significación del mecanismo de detección de cambios y el número de clasificadores base. Además, se realizó un estudio experimental que evidenció que el nuevo algoritmo se adapta eficientemente a cambios de concepto abruptos y es competitivo en cuánto a precisión con el resto de los algoritmos. También se comprobó estadísticamente que FASE-Boost obtuvo mejor rendimiento que los algoritmos propuestos en la literatura frente a conjuntos de datos reales.
