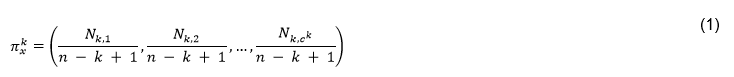INTRODUCCIÓN
Las enzimas son macromoléculas biológicas que actúan como catalizadores específicos durante los procesos biológicos, siendo el reconocimiento de su función mediante métodos computacionales robustos un problema abierto en Bioinformática. Una de las principales direcciones trazadas en este sentido está relacionada con considerar el número creciente de enzimas que tienen función validada experimentalmente. El desarrollo de métodos de aprendizaje con manejo de datos desbalanceados y con muestras pequeñas constituye una fuente potencial para la solución del problema (Li et al., 2018). Además, se hace necesario el uso de métodos de aprendizaje para manejar datos masivos cuando se requiere realizar búsquedas de secuencias desconocidas a gran escala, aspecto no considerado en los servidores disponibles y los artículos de referencia consultados (Shen & Chou, 2007) .
Un interés considerable de la comunidad científica se expresa en el sitio (http://www.cazy.org/) (Lombard et al., 2014) sobre la clasificación funcional de las enzimas cuyo trabajo es modificar y descomponer los carbohidratos [GHs (hidrolasas de glucósidos) y lyases] y aquellas involucradas en su biosíntesis, GTs (glicosiltransferasas). Típicamente, estas enzimas componen aprox. 1-2% del genoma de cualquier organismo. En el propio sitio, así como en su publicación insigne de referencia (Davies & Sinnott, 2008) se plantea que es necesario mejorar la forma de clasificar dichas enzimas y sus secuencias ya que se presentan incongruencias con las clasificaciones actuales de la Asociación Internacional de Unión de Bioquímica y Biología Molecular con los Números de la Comisión de Enzimas (CE). Se plantea que dichas clasificaciones ni tienen suficiente alcance para reflejar todos los GH, ni reflejan las especificidades estructurales y características mecánicas. Además, los números de la CE no pueden hacer frente a la amplia gama de especificidades. La presencia de divergencia en la evolución de un antepasado común a adquirir nuevas especificidades, y las convergencias en la evolución hacia una enzima similar significa que con frecuencia no hay correlación entre el número de la CE de una clase de enzima y las secuencias de las enzimas que realizan estas reacciones, además muchas de las enzimas no tiene número asociado. A su vez, en la propia referencia, se presenta como un gran desafío, el de clasificar un número creciente de enzimas provenientes de la secuenciación de genomas completos sin afectar el desempeño de esta clasificación. De lo anterior se deduce la necesidad de contribuir a la clasificación funcional de enzimas con nuevos métodos escalables basados en el aprendizaje automatizado capaces de manejar el desbalance en la multi-clasificación y las pocas secuencias clasificadas en las clases. En nuestro país, existe un interés marcado en la clasificación de secuencias de enzimas correspondientes a la familia Glicosil Hidrolasa-70 (GH-70) que están siendo estudiadas desde hace varios años por el Instituto Cubano de Investigaciones de los Derivados de la Caña de Azúcar (ICIDCA) (Fraga Vidal et al., 2011) por la utilidad biotecnológica de las mismas y por el efecto nocivo que pueden llegar a causar en la producción de azúcar, provocando pérdidas millonarias para la economía del país. Es por esto que estas enzimas GH-70 se han tomado en este trabajo como muestra para la validación de nuevos métodos de clasificación funcional en el nivel de subclase CE 3.
Como una tendencia en la clasificación de secuencias de proteínas o enzimas (AK Ong et al., 2007), principalmente en aquellas familias que contienen secuencias homólogas de baja similitud, como secuencias divergentes que pueden realizar una función similar, también conocidas como homólogos remotos, se presenta el uso y la integración de diversos descriptores libres de alineamiento de proteínas o enzimas como los k-mers (Davies & Sinnott, 2008; Meng et al., 2016). Específicamente, la integración de descriptores ha permitido elevar la calidad de la clasificación de ortólogos (secuencias homólogas con un ancestro común, generalmente, con función similar en especies diferentes) en trabajos realizados en el Centro de Investigaciones de Informática de la Universidad Central “Marta Abreu” de Las Villas (UCLV) (Galpert, 2016). A propósito, los descriptores de k-mers representan las secuencias como vectores con múltiples componentes asociadas a diferentes propiedades estructurales, y si son integrados con valores de k del 2 al 3 y del 2 al 4, constituyen vectores de alta dimensionalidad que han tenido que ser manejados de manera escalable mediante de técnicas de análisis de datos masivos como las disponibles en Apache Spark
Tomando estos antecedentes y partiendo de la consideración de que la similitud estructural define la similitud funcional, así como que pocas secuencias reportadas dentro de las familias enzimas han sido caracterizadas en cuanto a su actividad enzimática (por ejemplo, 58 de 501 dentro las GH-70), en este trabajo se pretende contribuir al desarrollo de métodos escalables de clasificación funcional de enzimas integrando descriptores libres de alineamiento, en específico, k-mers, con el aprendizaje semi-supervisado para conformar grupos de secuencias con patrones estructurales similares aprovechando el conocimiento previo de secuencias caracterizadas funcionalmente. De este modo el texto que sigue se ha dividido en dos partes: la Metodología Computacional donde se abordan las técnicas, instrumentos y métodos empleados para la recolección de los datos y los Resultados y Discusión donde se presentan y analizan los resultados del estudio y las proyecciones futuras.
MÉTODOS O METODOLOGÍA COMPUTACIONAL
Este trabajo intenta explorar el uso técnicas bioinformáticas disponibles para caracterizar funcionalmente las enzimas, como los descriptores libres de alineamiento basados en k-mers, por lo que el concepto y cálculo de los mismos queda explicado en la subsección Descriptores libres de alineamiento. Algunas de herramientas disponibles en el campo del aprendizaje automatizado para agrupar y clasificar las mismas como el aprendizaje no supervisado y semi-supervisado serán tratadas en la subsección Aprendizaje no supervisado y semi-supervisado. En la subsección Nuevos algoritmos de clasificación de enzimas se detallan las transformaciones realizadas a los algoritmos previamente referenciados. Seguidamente, algunos índices que permiten validar los algoritmos fueron mencionados en la subsección Medidas de validación internas y externas. Por último, la subsección Experimentación aparece la descripción del experimento realizado.
Descriptores libres de alineamiento
Los descriptores libres de alineamiento son métodos de extracción de rasgos estructurales intrínsecos de las secuencias mediante funciones que transforman la secuencia en un vector numérico para posteriormente derivar la similitud de un par de secuencias al comparar dichos vectores numéricos. Estos métodos se conocen como libres de alineamiento y muestran múltiples aplicaciones (Vinga, 2014; Vinga & Almeida, 2003; Zielezinski et al., 2017, 2019). Ejemplo de métodos libres de alineamiento son los basados en frecuencia de palabras (Gunasinghe et al., 2014; Melsted & Pritchard, 2011) los cuales se basan en funciones llamadas descriptores moleculares de la forma:
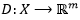 , donde una secuencia
, donde una secuencia  de longitud n es convertida a un vector de longitud r. De esta forma, los métodos basados en k-tuplas, k-palabras o k-mers, con
de longitud n es convertida a un vector de longitud r. De esta forma, los métodos basados en k-tuplas, k-palabras o k-mers, con  , realizan una correspondencia de una secuencia con un vector (1) cuyas componentes
, realizan una correspondencia de una secuencia con un vector (1) cuyas componentes  representan la frecuencia de subsecuencias de longitud k, siendo
representan la frecuencia de subsecuencias de longitud k, siendo  el total de todos los posibles k-mers del alfabeto finito
el total de todos los posibles k-mers del alfabeto finito 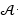 de c caracteres.
de c caracteres.
Como se ha mencionado anteriormente, en este trabajo se ha calculado el descriptor de 𝑘-mers para k = 2, 3 y 4. La dimensión de cada vector es como máximo 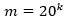 por lo que integrar varios valores de k en la comparación de pares de secuencias conlleva a elevar la dimensionalidad del problema de clasificación y buscar la forma de manejar tal dimensionalidad. Al integrar los 2 a 3-mers se obtendría una dimensión de 8400 columnas o rasgos correspondientes a las subsecuencias de longitud dos y tres que se encuentran dentro de las secuencias que se están analizando. Mientras al integrar los 2-mers, 3-mers y 4-mers correspondientes a las subsecuencias de longitud dos, tres y cuatro se obtendría una dimensión de 168400 columnas. En este trabajo se han combinado las facilidades de escalabilidad de Spark (Assefi et al., 2017) con la agregación de datos para lograr la integración de rasgos, aunque se pudieran explorar en trabajos futuros los métodos de reducción de la dimensionalidad o selección de rasgos relevantes, así como otras formas de representación de las secuencias(Li et al., 2018). Utilizando el enfoque de representación de k-mers la comparación de pares de vectores se realiza mediante medidas de similitud o disimilitud entre vectores. En (Galpert, 2016) son mencionadas variantes para calcular la disimilitud (o similitud) entre pares de vectores pero en este caso se ha seleccionado la correlación de Pearson (2) que es una métrica normalizada expresando similitud entre pares de vectores
por lo que integrar varios valores de k en la comparación de pares de secuencias conlleva a elevar la dimensionalidad del problema de clasificación y buscar la forma de manejar tal dimensionalidad. Al integrar los 2 a 3-mers se obtendría una dimensión de 8400 columnas o rasgos correspondientes a las subsecuencias de longitud dos y tres que se encuentran dentro de las secuencias que se están analizando. Mientras al integrar los 2-mers, 3-mers y 4-mers correspondientes a las subsecuencias de longitud dos, tres y cuatro se obtendría una dimensión de 168400 columnas. En este trabajo se han combinado las facilidades de escalabilidad de Spark (Assefi et al., 2017) con la agregación de datos para lograr la integración de rasgos, aunque se pudieran explorar en trabajos futuros los métodos de reducción de la dimensionalidad o selección de rasgos relevantes, así como otras formas de representación de las secuencias(Li et al., 2018). Utilizando el enfoque de representación de k-mers la comparación de pares de vectores se realiza mediante medidas de similitud o disimilitud entre vectores. En (Galpert, 2016) son mencionadas variantes para calcular la disimilitud (o similitud) entre pares de vectores pero en este caso se ha seleccionado la correlación de Pearson (2) que es una métrica normalizada expresando similitud entre pares de vectores 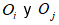 .
.
donde 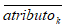 es el valor promedio que toma el atributok en el conjunto de datos.
es el valor promedio que toma el atributok en el conjunto de datos.
Los vectores representativos de las secuencias conforman un conjunto de datos denominado Kmers-k de vectores de valores reales de ocurrencia de subsecuencias de longitud k para cada secuencia de enzima. Se propone concatenar vectores para valores de k diferentes y luego aplicar correlación al vector resultante. Como primera combinación se propone integrar en un mismo conjunto de datos los Kmers-2 y Kmers-3 y como segunda combinación, la integración de los Kmers-2, Kmers-3 y Kmers-4 en otro conjunto.
Aprendizaje no supervisado y semi-supervisado
La agrupación en clústeres es uno de los problemas de análisis de datos más conocidos y estudiados. Constituye un área de investigación clave en el campo del aprendizaje, donde no hay supervisión sobre cómo se debe manejar la información. Podemos definir el agrupamiento particional como la tarea de agrupar los objetos de un conjunto de datos en k grupos, de modo que se pueda extraer nueva información de ellos. Un conjunto de datos X se compone de n objetos, y cada objeto se describe por u rasgos. Más formalmente, 𝑋= 𝑋 1 ,…., 𝑋 𝑛 con el i-ésimo objeto definido como 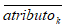 . Un algoritmo de agrupamiento típico asigna una etiqueta de clase li a cada objeto
. Un algoritmo de agrupamiento típico asigna una etiqueta de clase li a cada objeto 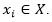 . Como resultado, obtenemos el conjunto de etiquetas
. Como resultado, obtenemos el conjunto de etiquetas  , que efectivamente divide X en k grupos no superpuestos ci que forman la partición. El criterio utilizado para asignar un objeto a un grupo dado es la similitud con el resto de los objetos en ese grupo, y la disimilitud con el resto de los objetos del conjunto de datos, y se puede obtener con algún tipo de medición de distancia (Anil Kumar Jain et al., 1999). Se desea que los objetos que pertenezcan al mismo grupo sean tan similares como se pueda y los objetos que pertenezcan a grupos diferentes sean tan diferentes como sea posible (Höppner et al., 1999; Kruse et al., 2007).
, que efectivamente divide X en k grupos no superpuestos ci que forman la partición. El criterio utilizado para asignar un objeto a un grupo dado es la similitud con el resto de los objetos en ese grupo, y la disimilitud con el resto de los objetos del conjunto de datos, y se puede obtener con algún tipo de medición de distancia (Anil Kumar Jain et al., 1999). Se desea que los objetos que pertenezcan al mismo grupo sean tan similares como se pueda y los objetos que pertenezcan a grupos diferentes sean tan diferentes como sea posible (Höppner et al., 1999; Kruse et al., 2007).
En cambio, el aprendizaje semi-supervisado es un paradigma de aprendizaje automatizado que surge de agregar información incompleta al aprendizaje no supervisado (Chapelle et al., 2006). Siguiendo este paradigma podemos incorporar información de fondo al proceso de agrupamiento, lo que resulta en un agrupamiento restringido, que es el tema principal del estudio presentado en (Triguero et al., 2015). El objetivo del agrupamiento restringido es encontrar una partición del conjunto de datos que cumpla con las características adecuadas del resultado de un método de agrupamiento, además de satisfacer un determinado conjunto de restricciones (González-Almagro et al., 2020).En otras palabras, el aprendizaje semi-supervisado es una rama del aprendizaje automatizado que resulta de combinar el aprendizaje supervisado y el no supervisado (Chapelle et al., 2006; Xiaojin Zhu, 2005). En el agrupamiento semi-supervisado, la información supervisada se puede tomar de diferentes formas, por ejemplo, pueden aplicarse restricciones must-link (se sabe que dos objetos están en el mismo grupo) y cannot-link (dos objetos se sabe que están en diferentes grupos) (Lange et al., 2005). También es posible que algunas asignaciones de grupos se conozcan de antemano. Un ejemplo para la incorporación de este último tipo de información es el uso de datos etiquetados para la “siembra en racimo”, como en (Basu et al., 2002), donde propusieron inicializar los grupos basados en los objetos para los que se conocen asignaciones de grupo.
En el problema de clasificación de las enzimas, al considerar la clasificación previa de algunas secuencias en la descripción detallada de la función enzimática expresada a través de la etiqueta CE resulta conveniente utilizar el aprendizaje semi-supervisado al ser pocas las secuencias etiquetadas. Como se había mencionado en la Introducción, en la experimentación de este trabajo se utiliza el conjunto de datos de enzimas GH-70 donde existen seis grupos de actividad enzimática los cuales serán inicializados con las 58 enzimas clasificadas, de 501 disponibles, en el sitio web CAZy.org/GH70_characterizedb, antes de comenzar el proceso de agrupamiento. La información de etiquetado previo también se utiliza en la etapa de validación mediante el uso de índices o medidas de validación externa que pueden ser combinados con índices de validación interna (Halkidi et al., 2002; Koutroumbas & Theodoridis, 2008) indicando en qué grado el agrupamiento es correcto o no (Höppner et al., 1999).
Para el agrupamiento semi-supervisado que se propone, primero es necesario profundizar en los siguientes tres algoritmos:
El algoritmo Combinatorio Lógico Global (Global Logical Combinatorial, GLC+) en (Ruiz-Shulcloper, s. f.; Ruiz-Shulcloper & Sánchez-Díaz, 2001). Este es un método de agrupamiento incremental que construye componentes conexas a partir de descripciones mezcladas e incompletas de objetos representadas en espacios no necesariamente métricos. Este método puede ser aplicado a muy grandes volúmenes de datos y por su naturaleza incremental permite inicializar los grupos con las secuencias etiquetadas e ir incrementando los mismos según las comparaciones de similitud entre la secuencia a analizar en cada paso y el resto de las secuencias por lo que puede ser transformado a agrupamiento semi-supervisado.
El algoritmo de agrupamiento no supervisado K-medias realiza la construcción de particiones (grupos) del conjunto de datos sobre la base del perfeccionamiento de algún índice, conocido también como función objetivo. En esencia, divide n objetos en un número positivo k de grupos, generalmente especificado a priori. El objetivo de este tipo de métodos es encontrar la mejor división de los datos en k grupos basada en una medida de similitud dada y conservar el espacio de particiones posibles en k subconjuntos solamente. La mayoría de los algoritmos que siguen esta técnica son esencialmente basados en prototipos, comienzan con una partición inicial, usualmente aleatoria, y proceden con su refinamiento (Han & Kamber, 2001). Este algoritmo funciona mejor con grupos que tienen forma convexa y requiere que el número de grupos a obtener se especifique a priori, por tanto requiere un cierto conocimiento del dominio, ya que es sensible a cómo se realizó inicialmente la partición. El algoritmo K-medias tiene una complejidad temporal O(Ikn), donde I se utiliza para indicar número de iteraciones, n el número de objetos y k el número de grupos.(Xiong et al., 2006), El K-medias también puede ser utilizado seleccionando previamente los centroides de los grupos como aparece en (Arai & Barakbah, 2007; Khan & Ahmad, 2004).. El algoritmo K-medias ofrece mejores resultados solo cuando las particiones iniciales están cerca de la solución final.(Anil K. Jain & Dubes, 1988).
El Ensamblado de Agrupamientos (Ensemble Clustering, EC) utilizado en (Abdallah & Yousef, 2020). Este método de agrupamiento reemplaza el espacio de datos por un espacio categórico basado en agrupación de conjuntos. El nuevo espacio categórico se define mediante el seguimiento de la membresía de los objetos en múltiples ejecuciones de algoritmos de agrupamiento.
En la subsección siguiente se explicarán en detalles los cuatro algoritmos semi-supervisados propuestos que resultan de transformar y combinar los tres algoritmos anteriores.
Nuevos algoritmos de agrupamiento de enzimas
De los tres algoritmos mencionados en la Subsección: Aprendizaje no supervisado y semi-supervisado se diseñó y modificó el código del método GLC+ convirtiéndolo en semi-supervisado ya que en su forma original la cantidad de grupos que se pueden formar con el método GLC+ es indeterminada, pero al ser reformado se limitó esta cantidad a seis grupos posibles a formar, correspondientes a la actividad enzimática. Además, en el GLC+ original los grupos comienzan vacíos y se van incrementando objetos Oi, cada vez que encuentran un objeto Oj semejante que pertenezca al agrupamiento Gk que cumplan la condición expresada en (3) donde 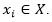 representa la similitud entre los objetos Oi yOj, y
representa la similitud entre los objetos Oi yOj, y  , el umbral de similitud.
, el umbral de similitud.
En el caso del GLC+semi-supervisado se tienen los grupos inicialmente con algunas enzimas de las que se conoce su clasificación.
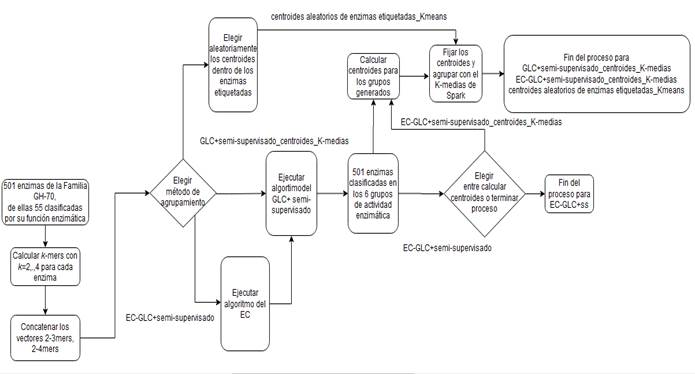
El pseudocódigo para este algoritmo de agrupamiento GLC+semi-supervisado aplicando como medida de similitud la expresada en (2) se muestra a continuación Figura 1:
En P1 se produce la concatenación de los vectores Kmers-k resultando un Kmersintegrados de 2 al 3-mers y de 2 al 4-mers para diferentes corridas del algoritmo. En P5 se verifica que el resultado de la correlación de Pearson entre los dos vectores cumpla con la expresión (3). El valor de 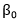 se calcula a partir de la matriz de semejanza entre todas las m secuencias de enzimas utilizando la expresión (4), ver (Ruiz-Shulcloper, s. f.) para más detalles.
se calcula a partir de la matriz de semejanza entre todas las m secuencias de enzimas utilizando la expresión (4), ver (Ruiz-Shulcloper, s. f.) para más detalles.
En P6 se determina con cual enzima de las etiquetadas de los seis grupos tiene mayor valor de similitud y es en ese grupo donde encontró la más similar que en P7 se agrupa a la enzima que se está analizando.
Se proponen cuatro nuevos métodos de agrupamiento semi-supervisado:
El primero, EC_GLC+semi-supervisado es el resultado de combinar el Ensamblado de Agrupamientos y el GLC+semi-supervisado, este comienza preparando un nuevo conjunto de datos como resultado de aplicar el Ensamblado de Agrupamientos para luego agrupar usando el GLC+semi-supervisado que ya incorpora información de fondo al proceso y hace que se cumplan las restricciones que se explicaron previamente.
El segundo denominado GLC+semi-supervisado_centroides_K-medias parte de ejecutar el GLC+semi-supervisado, determinar los centroides de esos grupos generados que ya aprovecha la información de las enzimas etiquetadas y aplicar finalmente K-medias fijándole esos centroides antes de iniciar el agrupamiento no dejando que sea la selección de los centroides de manera aleatoria, característica intrínseca del agrupamiento no supervisado que realiza el K-medias.
El tercero denominado EC_GLC+semi-supervisado_centroides_K-medias parte del resultado obtenido por el primer método propuesto, determinar los centroides de esos grupos generados que ya aprovecha la información de las enzimas etiquetadas y aplicar finalmente K-medias fijándole esos centroides antes de iniciar el agrupamiento.
El cuarto y último método, que denominaremos Centroides_aleatorios_de_enzimas_etiquetadas_K-medias parte de seleccionar una de las mejores combinaciones de los centroides escogidos aleatoriamente del grupo de enzimas etiquetadas y luego aplica K-medias con esos centroides.
EC_GLC+semi-supervisado
El algoritmo de transformación Ensemble Clustering (EC) consiste en ejecutar un algoritmo de agrupamiento (o múltiples algoritmos) varias veces con diferentes valores de parámetros donde cada ejecución produce una dimensión categórica (característica o rasgo) de los datos. Por ejemplo, ejecutar el algoritmo K-medias con diferentes valores de k = 1,..., N, generará un nuevo vector de datos con dimensión N. En otras palabras, dos objetos en el espacio del EC son idénticos si fueron asignados a los mismos grupos en toda iteración (k = 1,.., N). Todos los objetos que caen en el mismo clúster en las diferentes ejecuciones del agrupamiento constituyen un solo grupo y están representados por un solo objeto. Esta última aseveración será transformada ya que el objetivo que se pretende alcanzar no es el de crear tantos grupos como sea posible sino solamente los grupos conocidos de acuerdo a la clasificación de enzimas es por ello que se decide combinarlo con el GLC+semi-supervisado que previamente fue transformado para cumplir esa condición. Lo anterior se logra comparando los nuevos vectores que se generaron con los vectores asociados de las enzimas clasificadas, y los que resulten con mayor correlación se pueden considerar como del grupo al que pertenece la enzima clasificada de referencia. El número N de iteraciones a realizar es un parámetro ajustable iterativamente hasta que se logre un valor adecuado del índice de silueta.
GLC+semi-supervisado_centroides_K-medias
En el segundo método propuesto el proceso comienza con la ejecución del GLC+semi-supervisado, luego determina los centroides de esos grupos generados con la librería MLlib de Spark la cual en la sección Estadísticas proporciona la media de un conjunto de vectores. De este modo se calculan nuevos vectores centroides por cada uno de los seis grupos de actividad enzimática y esta información se le suministra al K-medias implementado también en la misma librería de Spark para fijarle los centroides a partir de los cuales comienza el agrupamiento.
EC_GLC+semi-supervisado_centroides_K-medias
En el tercer método propuesto el proceso comienza con la ejecución del Ensamblado de Agrupamientos, a ese nuevo conjunto de datos se le aplica el GLC+semi-supervisado, luego se determina los centroides de esos grupos generados con la librería MLlib de Spark. De este modo se calculan nuevos vectores centroides por cada uno de los seis grupos de actividad enzimática y esta información se le suministra al K-medias para fijarle los centroides, a partir de los cuales comienza el agrupamiento.
Centroides_aleatorios_de_enzimas_etiquetadas_K-medias
En el último método propuesto el proceso comienza al hacer combinaciones de seis enzimas escogidas aleatoriamente de los seis grupos de enzimas etiquetadas, se aplicó K-medias con esos centroides aleatorios, y se escogió aquella combinación que al calcularle el índice de silueta diera el mayor valor con relación al resto de las combinaciones.
Medidas de validación internas y externas
Las medidas internas se utilizan para medir la densidad y la cohesión entre pares de objetos de un mismo grupo. Se escogió como medida interna para validar los resultados de este trabajo el índice de silueta que es el promedio, sobre todos los grupos, del ancho de la silueta de sus puntos. Si x es un objeto en el clúster ck y nk es el número de objetos en Ck, entonces, el índice de silueta de x está definido por la relación expresada en (5):
Donde a(x) en (5) es el promedio de las distancias entre x y todos los otros objetos en Ck y b(x) en (7) es el mínimo de los promedios de las distancias d(x,y) entre x y los objetos de los otros clústeres.
Finalmente, el índice de silueta global (8) está definido como sigue, siendo K el número de clústeres y nk la cantidad de objetos en cada clúster:
Para un objeto x dado, el ancho de su silueta varía de -1 a 1. Si el valor está cerca de -1, significa que el objeto está más cerca, en promedio, de otro grupo que de aquél al que pertenece. Si el valor es cercano a 1, significa que la distancia promedio a su propio grupo es significativamente menor que a cualquier otro grupo. Valores altos del índice silueta global indican grupos más compactos y bien separados. El cálculo de este índice tiene una alta complejidad; sin embargo, investigaciones actuales lo utilizan para la validación del agrupamiento (Brun et al., 2007). En este trabajo se utilizó para guiar el agrupamiento en el Ensamblado de Agrupamientos (EC) ya que sirvió de indicador para determinar cuántas ejecuciones N del algoritmo de agrupamiento K-medias serían necesarias para lograr grupos más separados y compactos.
Por otra parte, las medidas externas se basan en las etiquetas conocidas. Algunas medidas externas utilizan las ideas de precisión (precision) y cubrimientoc (recall) del campo de la recuperación de información y las adaptan a la validación del agrupamiento. La precisión (Pr) y el cubrimiento (Re) se calculan mediante las expresiones (9)(10), respectivamente, para un grupo j y una clase i dados, donde nij es el número de objetos de la clase i en el grupo j, nj es el número de objetos del grupo j y nj es el número de objetos de la clase i.
La medida-F (F-measure) se obtiene calculando la media armónica de precisión y cubrimiento como se aprecia en (11).
Si ( = 1 entonces  coincide con precisión, y si ( = 0 entonces
coincide con precisión, y si ( = 0 entonces  coincide con cubrimiento. En el caso que ( = 0.5 significa igual peso para precisión y cubrimiento (Baeza-Yates & Frakes, 1992). Un valor global, de la medida-F global (Overall F-measure; OFM), se calcula mediante el promedio de los valores por clase de la medida-F sobre todos los grupos (Steinbach et al., 2000). Esta medida-F intenta capturar cuánto los grupos del agrupamiento obtenido se hacen corresponder correctamente con los grupos de referencia o clases incluso cuando existe desbalance en la cantidad de objetos por clase (Rosell et al., 2004). En resumen, las medidas externas: precisión, cubrimiento y medida-F fueron utilizadas para medir la calidad de los agrupamientos obtenidos en este trabajo.
coincide con cubrimiento. En el caso que ( = 0.5 significa igual peso para precisión y cubrimiento (Baeza-Yates & Frakes, 1992). Un valor global, de la medida-F global (Overall F-measure; OFM), se calcula mediante el promedio de los valores por clase de la medida-F sobre todos los grupos (Steinbach et al., 2000). Esta medida-F intenta capturar cuánto los grupos del agrupamiento obtenido se hacen corresponder correctamente con los grupos de referencia o clases incluso cuando existe desbalance en la cantidad de objetos por clase (Rosell et al., 2004). En resumen, las medidas externas: precisión, cubrimiento y medida-F fueron utilizadas para medir la calidad de los agrupamientos obtenidos en este trabajo.
Experimentación
En el conjunto de datos utilizado en la experimentación se tienen 501 enzimas GH-70, de ellas 58 clasificadas pertenecientes a: 43 del primer grupo, dos del segundo grupo, dos del tercer grupo, cuatro del cuarto grupo, dos del quinto grupo y una del sexto grupo. De las 58 enzimas, la enzima “CDX66820.1” tiene doble clasificación lo que significa que tiene doble actividad enzimática, y no se utilizó entre las clasificadas para no introducir confusión durante el agrupamiento. Por otra parte, las enzimas: “P08987” y “P49331” no se encuentran entre las 501 secuencias de las enzimas para clasificar. De lo anterior se deriva que de las 58 clasificadas serán utilizadas 55 enzimas.
Con el objetivo de esclarecer el flujo de procesos seguido en el agrupamiento durante la experimentación, la (Figura 2) muestra la entrada de secuencias al proceso de extracción de rasgos mediante los descriptores libres de alineamiento, en este caso, los k-mers, la integración de los mismos, la transformación de datos en el Ensamblado de Agrupamientos, la secuencia a seguir en cada método propuesto y la ubicación final de las enzimas en los grupos de actividad enzimática reportados en CAZY.
Al realizar varias iteraciones con el Ensamblado de Agrupamientos, se encontró que para valores de k (número de grupos a formar con el algoritmo K-medias) entre 45 y 50 los valores del índice de silueta oscilaban entre 0.56 aproximadamente siendo éste el valor más alto en comparación a -0.0097 que es el valor más bajo encontrado, el cual indica demasiados o muy pocos elementos similares en el grupo. Por esta razón, se escogió N igual 50 como el número de ejecuciones a realizar. Para proceder a aplicar el Ensemble Clustering se realizaron corridas del K-medias para k desde 2 hasta 50, para los Kmers integrados de 2 al 3-mers y de 2 al 4-mers. Cada corrida se guardó en un archivo de tipo CSV, los cuales fueron integrados en un archivo por cada Kmers integrados.
Los resultados obtenidos por los cuatro métodos con las distintas medidas de validación se exponen en la sección de Resultados y Discusión.
RESULTADOS Y DISCUSIÓN
Los cuatro métodos propuestos en la sección anterior fueron implementados en lenguaje de programación Scala. Se utilizaron además las librerías MLlib y ML implementadas en Spark para el análisis de grandes volúmenes de datos como los k-mers, así como el K-medias para realizar agrupamientos y el cálculo de (2) por pares de vectores implementado en Spark.
En la (Tabla 1) se muestra la predicción obtenida por los cuatro métodos de agrupamiento semi-supervisados propuestos.
Como se puede apreciar en el método EC_GLC+semi-supervisado: el 85.9% de las enzimas fueron ubicadas en el grupo uno, el 1.59% en el grupo dos, el 0.69% en el grupo tres, el 7.58% en el grupo cuatro, el 2.49% en el grupo cinco y el 1.69% en el grupo seis, siendo la mayoría de las enzimas clasificadas en el grupo uno y en segundo lugar, en el grupo cuatro. Esta predicción es similar a la proporción de ubicación por grupo de las 55 enzimas clasificadas, donde el 78% de las clasificadas están en el grupo uno y el 9.09% está en el grupo cuatro. El resto de las clasificadas solo posee una o dos enzimas en los grupos dos, tres y seis. Por su parte el método GLC+semi-supervisado_centroides_K-medias obtiene 8.18% de enzimas clasificadas en grupo uno, 2.59% en el grupo dos, 7.38% en el grupo tres, 17.46% en grupo cuatro, 45.20% en grupo cinco y 19.15% en grupo seis, ubicando la mayor parte de las enzimas entre los grupos cinco y seis, resultados no similares a la proporción de ubicación por grupo de las enzimas previamente etiquetadas. En el caso del método EC_GLC+semi-supervisado_centroides_K-medias el 10.87% fue ubicado en el grupo uno, el 11.87% en el grupo dos, el 6.98 % en el grupo tres, el 23.65% en el grupo cuatro, el 12.97% en el grupo cinco y el 33.63% en el grupo seis, por lo que la mayor cantidad de enzimas fueron ubicadas en los grupos seis y cuatro, lo cual dista de la proporción original de las etiquetadas. Por último, en el caso del método Centroides_aleatorios_de_enzimas_etiquetadas_K-medias, el 35.22% fueron asignadas en el grupo uno, el 7.88% en el grupo dos e igual % en el grupo tres, el 38.62% en el grupo cuatro, el 1.99% en el grupo cinco y el 8.38% en el grupo seis, ubicando la mayor cantidad de enzimas entre los grupos uno y tres, lo cual se acerca un poco más a la proporción de los datos etiquetados.
En las predicciones realizadas por los cuatro métodos propuestos para las enzimas de las que ya se conoce su clasificación se encontró que en el caso del método EC_GLC+semi-supervisado con el uso de los k-mers del 2 al 3 y del 2 al 4 se realizó una incorrecta clasificación en la enzima “AAU08015.1” que se conoce previamente pertenece al grupo dos y fue ubicada erróneamente en el grupo cinco, el resto de las enzimas fueron ubicadas correctamente.
Por su parte, en el caso del método GLC+semi-supervisado_centroides_K-medias en la mayoría de las enzimas se realizó una incorrecta clasificación sólo realizó una correcta clasificación en las enzimas siguientes:
Con el uso de los k-mers del 2 al 3
“BAA26114.1”, “AAN58705.1” que se conoce previamente que pertenecen al grupo uno y fueron ubicadas en ese mismo grupo.
“CDX66896.1”, “ABP88726.1” que se conoce previamente que pertenece al grupo cinco y fueron ubicadas en ese mismo grupo.
“AOR73699.1”fue clasificada correctamente en el grupo seis
Con el uso de los k-mers del 2 al 4
“AJE22990.1”, “ACB62096.1” que se conoce previamente que pertenecen al grupo cuatro y fueron ubicadas en ese mismo grupo.
“CDX66896.1”, “ABP88726.1” que se conoce previamente que pertenecen al grupo cinco y fueron ubicadas en ese mismo grupo.
En el caso del método EC_GLC+semi-supervisado_centroides_K-medias en la mayoría de las enzimas se realizó una incorrecta clasificación sólo realizó una correcta clasificación en las enzimas siguientes:
Con el uso de los k-mers del 2 al 4
“BAA90527.1”, “AAS79426.1”, “CCK33643.1” que se conoce previamente que pertenecen al grupo uno y fueron ubicadas en ese mismo grupo.
En el caso del método Centroides_aleatorios_de_enzimas_etiquetadas_K-medias en la mayoría de las enzimas se realizó una incorrecta clasificación sólo realizó una correcta clasificación en las enzimas siguientes:
Con el uso de los k-mers del 2 al 4
“CAA77898.1”, “AAA26896.1”, “AAA26898.1”, “BAA14241.1”, “BAA02976.1”, “AAC41412.1”, “AAC41413.1”, “AAB95453.1”, “AAD10952.1”, “BAA90527.1”, “CAB76565.1”, “AAG38021.1”, “AAG61158.1”, “BAC07265.1”, “AAN58619.1”, “AAN38835.1”, “AAS79426.1”, “AAQ98615.2”, “AAX76986.1”, “ABC75033.1”, “ABF85832.1”, “BAF62337.1”, “BAF96719.1”, “ACA83218.1”, “ACK38203.1”, “ACT20911.1”, “ACY92456.2”, “ADB43097.3”, “CCF30682.1”, “AFP53921.1”, “CCK33643.1”, “CCK33644.1”, “AHU88292.1”, “CDX67012.1”, “CDX66895.1”, “CDX66641.1”, “AKE50934.1” que se conoce previamente que pertenecen al grupo uno y fueron ubicadas en ese mismo grupo.
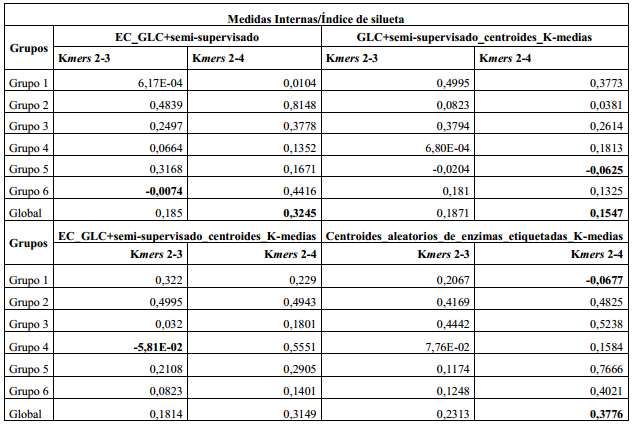
Como se había mencionado en la sección anterior, se utiliza para validar el agrupamiento el índice de silueta como medidas interna y como medida externa: precisión, cubrimiento y medida-F. En la (Tabla 2) se aprecian los valores calculados para el índice de silueta de los dos métodos con sus respectivas dos combinaciones de los k-mers.
El valor más bajo del índice de silueta por grupo en el caso del método EC_GLC+semi-supervisado lo tiene el grupo seis con el uso de los k-mers 2 al 3, en el método GLC+semi-supervisado_centroides_K-medias lo tiene el grupo cinco con el uso del k-mers del 2 al 4, en el método EC_GLC+semi-supervisado_centroides_K-medias se obtuvo en el grupo cuatro con el uso de 2 a 3-mers, en el método Centroides_aleatorios_de_enzimas_etiquetadas_K-medias en el grupo uno con el uso de los k-mers del 2 al 4, estos valores bajos sombreados en Negrita en la (Tabla 2) indican que las enzimas están más cerca, como promedio, de otro grupo que de éste donde fueron ubicadas. Por otro lado el valor más bajo del índice de silueta global lo tiene el método GLC+semi-supervisado_centroides_K-medias con el uso de los k-mers del 2 al 4 y el valor más alto se logró en el método Centroides_aleatorios_de_enzimas_etiquetadas_K-medias seguido del EC_GLC+ semi-supervisado con el uso de los 2 a 4-mers en ambos casos.
Aunque los valores del índice de silueta global para ambos métodos no son significativamente buenos por no estar por encima de 0.5 o más próximos a 1, se pudieran considerar como valores moderados, similares a los ofrecidos por el K-medias implementado en la librería ML de Spark, que al agrupar las enzimas usando k-mers 2 y 3 obtiene un índice de silueta de 0.19711619160997274 y 0.12133373673005655 con el uso de los k-mers del 2 al 4, valores similares, e incluso más bajos, que los obtenidos por algunos de los cuatro métodos con el uso de los 2 a 4-mers. Además, señalar que esta familia de enzimas posee enzimas muy similares a algunas que incluso tienen doble clasificación, como el caso de una de las etiquetadas que no se empleó para no generar confusión durante el agrupamiento, es decir, que tienen características que las pueden ubicar en más de un grupo al mismo tiempo. Todo esto explica los valores bajos del índice de silueta.
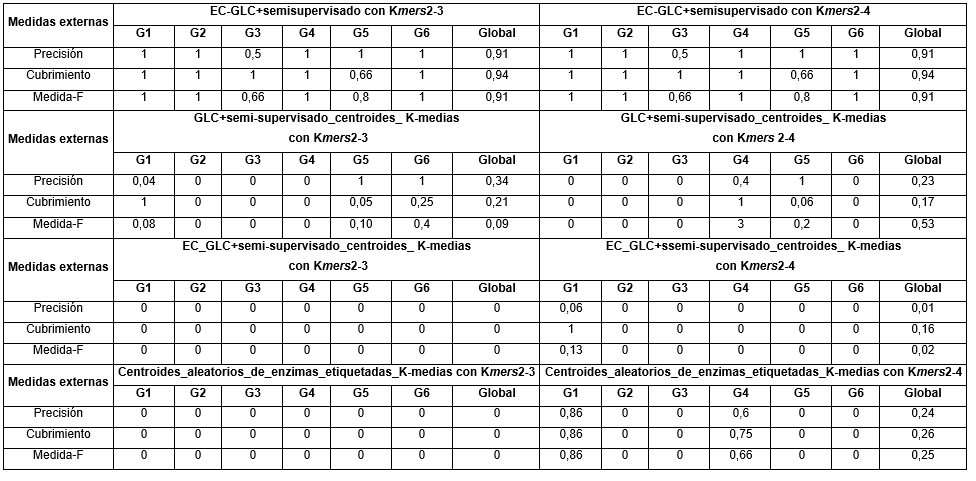
En el caso de las medidas externas, a continuación se muestran en (Tabla 3) los valores obtenidos para los dos métodos propuestos.
Como se puede apreciar los valores obtenidos para las medidas externas del método EC-GLC+ semi-supervisado fueron significativamente buenas con el uso de las dos combinaciones de k-mers con valores por encima de 0.91 en el peor de los casos. En Cubrimiento se obtuvieron los mejores valores con 0.94 en los dos casos.
En el caso del método GLC+semi-supervisado_centroides_K-medias los resultados no fueron positivos y fueron realmente muy bajos, con valores por debajo de 0.5. El peor valor se obtuvo en la medida-F con el uso de los k-mers del 2 al 3, sin embargo, en Precisión y Cubrimiento con el uso de estos k-mers se obtuvieron valores más altos que con el uso de los k-mers del 2 al 4.
En el caso de los método EC_GLC+semi-supervisado_centroides_K-medias y Centroides_aleatorios_de_enzimas_etiquetadas_K-medias los resultados tampoco fueron positivos. Al no obtener ninguna enzima de las etiquetadas bien clasificada con el uso de los k-mers del 2 al 3 entonces fue imposible obtener un valor mayor que cero para las tres medidas externas y con el uso de los k-mers del 2 al 4 se obtuvieron valores muy por debajo 0.30 de manera global. De manera general los valores de las medidas externas obtenidos en el primer método fueron mucho mejores que los obtenidos con los restantes métodos.
CONCLUSIONES
Con la propuesta de cuatro algoritmos para el agrupamiento que permiten incluir información disponible sobre el conjunto de datos, es posible realizar el agrupamiento de manera semi-supervisada. En los cuatro métodos se obtuvieron 6 clústeres correspondientes a la actividad enzimática.
Al validar el agrupamiento resultaron aceptables los valores del índice de silueta ofrecido por los cuatro métodos pero con el uso de los 2 a 4-mers e incluso mejores que los obtenidos por el K-medias de Spark. El mejor valor de silueta (0.37) se obtuvo con Centroides_aleatorios_de_enzimas_etiquetadas_K-medias. En la validación externa fueron promisorios los valores obtenidos por el método EC-GLC+semi-supervisado para los índices considerados, predominando el valor 0.91 en la medida-F para las distintas combinaciones de k-mers. El uso de otras medidas de similitud, y/o de otras formas de agregación o integración de la información basadas en la reducción de la dimensionalidad o la selección de los rasgos relevantes, junto a mejoras en el agrupamiento, pudieran mejorar los valores de los índices de validación para la clasificación de la actividad enzimática.
Por otra parte, el uso de Spark garantiza el manejo de rasgos de alta dimensionalidad como los k-mers, que permiten extraer información de la estructura de las secuencias, y además, deberá garantizar la escalabilidad de los algoritmos cuando se incremente el número de procesadores y de secuencias a clasificar, así como obtener bajos tiempos de ejecución en un clúster de computadoras.