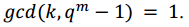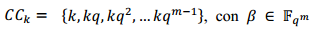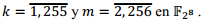Servicios personalizados
Español (pdf)
Articulo en XML
Referencias del artículo
Enviar articulo por email
Citado por SciELO 
Similares en
SciELO 
Permalink
INTRODUCCIÓN
La teoría de los campos finitos (Lidl, Niederreiter, 1994), (Mullen, Panario, 2013) es una rama del álgebra moderna que desempeña un papel importante en diversas aplicaciones dentro de las áreas de ingeniería eléctrica (Golomb, Gong, 2005), ciencias de la computación (Menezes, Van Oorschot, Vanstone, 1997), matemáticas (Mullen, Panario, 2013), entre otras.
En las últimas décadas los campos finitos han sido utilizados como una herramienta poderosa en la construcción de sistemas computacionales con aplicación específica en diversas áreas tales como la criptografía (Menezes, Van Oorschot, Vanstone, 1997) y la codificación algebraica (MacWilliams, Sloane, Sloane, 1983) . Entre las concepciones más importantes sobre campos finitos se encuentra la teoría de los polinomios sobre los campos finitos, la cual resulta fundamental para la investigación de las estructuras algebraicas de los campos finitos y sus aplicaciones. La utilización de una clase especial de polinomios, los llamados polinomios primitivos, es de gran utilidad en el diseño de algunos componentes de algoritmos criptográficos (Daemen, Rijmen, 2002) debido a sus características matemáticas (Junod, Vaudenay, 2004).
En los sistemas de cifrado en flujo estos se utilizan como polinomio característico en los registros de desplazamiento con retroalimentación lineal (Golomb, 1982) para la generación de sucesiones recurrentes lineales de período máximo. El valor del período de estas sucesiones está determinado por las propiedades de su polinomio mínimo. Para que la sucesión recurrente lineal tenga período máximo, es necesario y suficiente que su polinomio mínimo sea un polinomio primitivo.
Por otro lado, en los sistemas de cifrado en bloques, las matrices MDS (Maximum Distance Separable) (Junod, Vaudenay, 2004) son uno de los componentes más utilizados en los últimos diseños de estándares de cifrado (Daemen, Rijmen, 2002) debido a que garantizan altos valores de difusión. Los polinomios primitivos sobre extensiones de campos finitos son utilizados en la construcción de este tipo de matrices (Freyre, Díaz, Diaz, Perez, 2014).
Además, los polinomios primitivos son útiles en la teoría de la codificación algebraica (MacWilliams, Sloane, 1983) debido que a partir de estos se construyen códigos correctores de errores como los códigos Goppa (Valentijn, 2015), utilizados en la construcción de algoritmos asimétricos resistentes a la computación post cuántica.
En la literatura existen varios algoritmos para la generación de polinomios primitivos sobre campos finitos (Madarro, 2017). Algunos de estos algoritmos poseen una complejidad de orden cúbico (Shoup, 2009) o superior (Saxena, McCluskey, 2004). Mientras el propuesto en (Rifà, Borrell,1995) basa su diseño a la utilización de hardware específico y el presentado en (da Silva Filho, Lima Filho, 1993) hace depender su complejidad en la selección de algoritmos para la factorización de polinomios.
Otras interesantes propuestas son los algoritmos propuestos en (Shoup, 1999) y en (Di Porto, Guida, Montolivo, 1992), ambos están basados en la teoría de los registros de desplazamiento y las sucesiones recurrentes lineales. No obstante, existe otra vía teórica relacionada con la generación de polinomios primitivos basada en la obtención de los cosetos q-ciclotómicos y la construcción de polinomios mínimos (Gordon, 1976) (Lidl, Niederreiter, 1994) (Shoup, 2009) (Shoup, 1999) que permite un sencillo acople con cualquier esquema de software y un costo computacional razonable. En (Rifà, Borrell,1995), cuya propuesta posee la mejor complejidad, se utiliza una idea similar, pero desde un punto de vista de hardware.
En este trabajo se presenta, utilizando conceptos y propiedades del álgebra en campos finitos y la teoría de números, un algoritmo para la generación de polinomios primitivos sobre campos finitos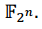 
Preliminares
Un polinomio 
se dice que es irreducible sobre Fq si 𝑓 tiene grado positivo y 𝑓 = 𝑏𝑐 con 𝑏, 𝑐 ∈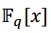 
.implica que 𝑏 o 𝑐 es un polinomio constante.(Lidl, Niederreiter, 1994) (Mullen, Panario, 2013).
Si f es un polinomio irreducible en 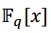de grado m, entonces 𝑓 tiene una raíz 𝛼 en
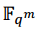. Además, todas las raíces de f son simples y están dadas por los m distintos elementos de
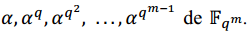. (Lidl, Niederreiter, 1994)
Sea B un elemento de 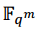el polinomio mínimo de B sobre 
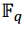es el polinomio mónico 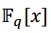de menor grado que tiene a B como raíz. Sea 
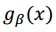el polinomio mínimo de 
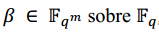entonces:
El polinomio 
es irreducible sobre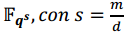
.
El grado de
= d con d divisor de m y sus raíces son B y sus conjugados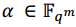
respecto a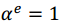 
De esta manera, se puede escribir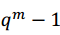 
como
Para
, el menor entero e tal que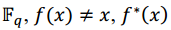 
se denomina orden de a y se denota por ord(a). Si ord(a)= 
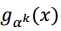, entonces a es llamado elemento primitivo 
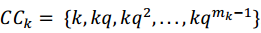y todos los elementos distintos de cero de 
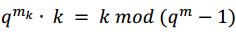pueden ser expresados como potencias de a. Los elementos primitivos de 
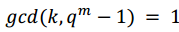son los ak tal que
.
Un polinomio f(x) de grado m es llamado primitivo sobre Fq si es el polinomio mínimo sobre Fq de un elemento primitivo en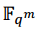. Sea f(x) un polinomio de grado m sobre Fq’ el polinomio reverso f*(x) de f(x)está definido como
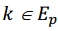. Si f(x) es irreducible sobre 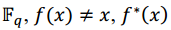es irreducible. Si f(x) es primitivo, su reverso también lo es. (Lidl, Niederreiter, 1994) (Mullen, Panario, 2013)
Sea a es un elemento primitivo de 
Sea 
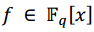el polinomio mínimo del elemento ak. Utilizando los cosetos ciclotómicos modulo qm-1, denotados como
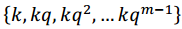, donde mk es el menor entero tal que
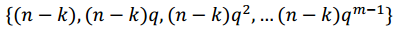, es posible escribir la siguiente caracterización de polinomios irreducibles y primitivos:
Todos los polinomios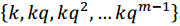
, tal que CCk tiene cardinalidad m, constituyen los polinomios irreducibles distintos de grado m sobreFq.
Los polinomios irreducibles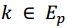
, tal que
, son todos los polinomios primitivos distintos de grado m sobre Fq.
Generación de polinomios primitivos
La idea del algoritmo (Madarro, 2017) es basar el problema de la generación de polinomios primitivos sobre extensiones de campos finitos en la construcción de los cosetos q-ciclotómicos módulo qm-1.
Donde d*(x) es el polinomio mónico reverso del polinomio d(x) y mcd(.) es la función que calcula el máximo común divisor. Se puede observar que el grado m del polinomio de entrada g irreducible sobre Fq utilizado para definir el campo finito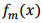 
coincide con el grado de los polinomios primitivos que se desean generar. Por otro lado, si se desea generar una cantidad fija de polinomios primitivos, solo es necesario construir una condición de parada para 𝑥 cuando su valor llegue a la cantidad deseada.
La obtención de los cosetos q-ciclotómicos se realiza mediante la obtención del conjunto Ep de los números primos relativos con el orden del grupo multiplicativo Fqm* y luego determinar, para cada número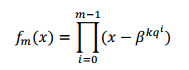 
, el conjunto 
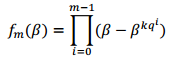módulo qm-1. (Cuellar, Morgado, Sosa 2015)
Un problema común es construir cosetos q-ciclotómicos repetidos. Para minimizar la ocurrencia de este caso se verifica para cada k si es coseto líder, puesto que el coseto líder es el menor de los elementos del coseto q- ciclotómico. Para realizar el paso 4 del algoritmo y determinar si un entero positivo k es un coseto líder se utilizó el siguiente algoritmo.
Sea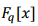 
el polinomio primitivo asociado al coseto 
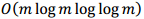. En el coseto q-ciclotómico 
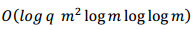cada elemento es el inverso multiplicativo de algún elemento del coseto
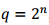, luego el polinomio asociado a este coseto q-ciclotómico es el polinomio reverso de f y por lo tanto también es primitivo.
De esta manera, encontrando cada elemento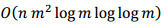 
se estarían determinando dos cosetos 𝑞-ciclotómicos y a su vez dos polinomios primitivos. Luego, para obtener todos los
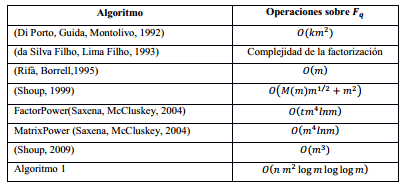, solo es necesario recorrer la mitad del espacio de búsqueda.
Luego de obtenido cada coseto q-ciclotómico, se realiza el cómputo del polinomio primitivo a partir de los elementos de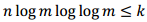
, cuyos exponentes integran el coseto q-ciclotómico, 
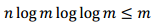un elemento primitivo. Esto es debido a que los elementos que pertenecen a s constituyen las raíces de un polinomio primitivo de grado m sobre Fq. Así, cada polinomio primitivo 
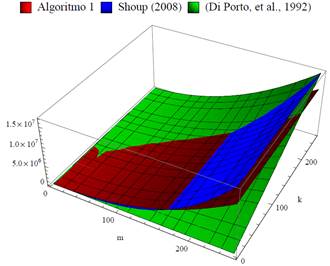de grado m puede obtenerse mediante la siguiente expresión.
donde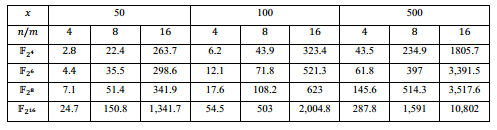 
se corresponde con el polinomio mínimo del elemento B.
Para el cómputo del polinomio mínimo 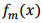(paso 9 del Algoritmo 1) normalmente se utilizan o(m2)operaciones sobre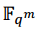. No obstante, en (Gordon, 1976) se proporciona una forma de obtener el polinomio mínimo de una forma más eficiente en cuanto a la cantidad de operaciones, mediante la expresión
Utilizando el Algoritmo 3 basado en la teoría descrita en (Gordon, 1976) se realizan solo o(m) operaciones sobre.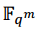
Complejidad computacional
Los pasos 6 y 9 son los de mayor costo computacional en el Algoritmo 1, correspondiente al cálculo del coseto 𝑞-ciclotómico y el cómputo del polinomio mínimo, respectivamente. Es conocido que los elementos del conjunto s se pueden obtener en O(m log q) operaciones sobre 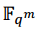(Von Zur Gathen, Panario, 2001) (Shoup, 2009), mediante sucesivas potencias a la q y un costo mínimo de almacenamiento, mientras el polinomio mínimo en O(m) operaciones sobre 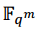utilizando el método propuesto en (Gordon, 1976).
Para el cómputo de polinomios primitivos se utilizó la representación en base polinomial de 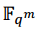sobre Fq, donde cada elemento de 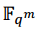es representado como un polinomio en 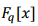de grado menor que m. En tal representación el costo de ejecución del Algoritmo 1 está dado por O(m log q M) operaciones sobre Fq, donde M es el costo en operaciones de la multiplicación. Utilizando el mejor método de multiplicación (Schönhage, Strassen, 1971), con 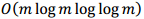operaciones sobre Fq, se realizan 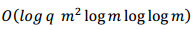operaciones sobre Fq. En este trabajo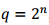, por lo que el costo de ejecución se puede expresar como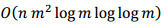operaciones sobre Fq.
RESULTADOS Y DISCUSIÓN
En la Tabla 1 se presenta un resumen de la complejidad computacional, en base a la cantidad de operaciones sobre Fq, de los algoritmos referenciados incluyendo el algoritmo propuesto.
Donde t es el número de factores de 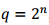y k es el exponente de un elemento primitivo del campo finito Fq. En el caso del algoritmo (da Silva Filho, Lima Filho, 1993) la complejidad puede sustituirse en dependencia del algoritmo que se utilice para factorizar polinomios sobre campos finitos (Von Zur Gathen, Panario, 2001).
Cuando 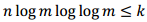la complejidad del Algoritmo 1 es comparable con la del obtenido (Di Porto, Guida, Montolivo, 1992). Mientras que en el caso 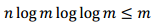el Algoritmo 1 es comparable a la complejidad del algoritmo en (Shoup, 2009) .
A menudo es necesario generar polinomios primitivos de varios grados sobre un mismo campo finito. Este es uno de los escenarios que favorece la utilización del Algoritmo 1 puesto que al fijar el campo finito, el grado m de los polinomios es el valor que determina el costo de generar los polinomios primitivos deseados al poder considerar n constante. Este escenario es una aplicación práctica real debido a que, por ejemplo, los algoritmos criptográficos trabajan sobre un campo finito específico fijo (Daemen, Rijmen, 2002).
En la Figura 1 se puede observar cómo se comporta la complejidad del algoritmo presentado en contraste con la complejidad correspondiente a los algoritmos (Shoup, 2009) y (Di Porto, Guida, Montolivo, 1992) sobre el campo finito fijado F2b para varios valores de m y k.
Se observa como existen valores de m y k a partir de los cuales el costo computacional del Algoritmo 1 es inferior a los casos (Shoup, 2009) y (Di Porto, Guida, Montolivo, 1992). Estos resultados muestran la importancia de seleccionar adecuadamente el valor de k en (Di Porto, Guida, Montolivo, 1992).
La Tabla 2 muestra el tiempo en segundos de la ejecución del Algoritmo 1, sin la utilización de tablas precomputadas para las operaciones aritméticas sobre campos finitos F2n, variando la cardinalidad n, la cantidad x de polinomios primitivos generados y el grado m de los polinomios primitivos a generar. Lo experimentos se realizaron en una Intel Pentium Dual Core de 1.3 Ghz.
La cardinalidad de los campos finitos aumenta exponencialmente en base a la dimensión n del campo finito, de esta manera un aumento en la dimensión n del campo finito influye en el tiempo requerido para generar los polinomios primitivos. No obstante, la mayor influencia, basado en la propia complejidad del Algoritmo 1, es el aumento del grado m de los polinomios primitivos a generar (Ver Tabla 2).
CONCLUSIONES
En el presente trabajo se propuso un algoritmo para la obtención de polinomios primitivos sobre extensiones de campos finitos de característica dos. Las bases teóricas sobre las cuales se basa el diseño del algoritmo están determinadas por la teoría de los cosetos q-ciclotómicos y los elementos primitivos para la construcción de polinomios mínimos. Para la construcción del algoritmo se transformó el problema de la búsqueda de polinomios primitivos sobre extensiones de campos finitos en la obtención de los cosetos q-ciclotómicos sobre campos finitos, el cual consiste en la búsqueda de los números primos relativos con el orden del grupo multiplicativo de Fqm.
Se determinó la complejidad del algoritmo presentado y se comparó con los algoritmos reportados en la literatura. El algoritmo propuesto tiene una complejidad inferior a varios algoritmos reportados en la literatura y mejora a otros bajo las condiciones descritas. Este algoritmo constituye una herramienta importante en aplicaciones prácticas pues puede ser implementada sin dificultad en software y puede ser utilizada para polinomios primitivos sobre extensiones de campos finitos.
En trabajos futuros se investigará el uso de bases normales y torres de campos finitos sobre el Algoritmo 1 con el objetivo de mejorar su complejidad computacional. Así como, realizar la implementación en paralelo para disminuir su tiempo de ejecución.
