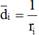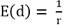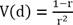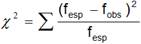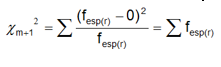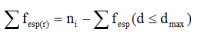Servicios personalizados
Español (pdf)
Articulo en XML
Referencias del artículo
Enviar articulo por email
Citado por SciELO 
Similares en
SciELO 
Permalink
INTRODUCCIÓN
Las secuencias categóricas están presentes en la naturaleza y en la actividad humana: desde la sucesión de aminoácidos presentes en una proteína (Santoni, 2016), hasta el comportamiento de las fallas en un proceso industrial (Coit, 2018) o la sucesión de eventos reportados en un estudio sociológico o económico (Chou, 2020).
Entre los paradigmas de modelación de secuencias categóricas más utilizados destacan las cadenas o procesos de Markov (Ramaekers, 2019) y las técnicas propias del análisis de fiabilidad de sistemas como los modelos exponenciales y de Weibull para la obtención de valores esperados en variables involucradas en procesos industriales y tecnológicos (Elabatal, 2016) (Beyer, 2018).
El estudio de la aleatoriedad en secuencias categóricas es relevante para la obtención de modelos estadístico-matemáticos y la comprensión de su comportamiento (Traylor, 2017). La aleatoriedad es una propiedad fundamental en el análisis estadístico. Es una de las condiciones inherentes a la teoría de muestreo y de hecho está presente en casi todas las pruebas de hipótesis que se realizan en estadística inferencial. (Shen, 2018)
La aleatoriedad (para secuencias categóricas) puede valorarse bajo diferentes raseros tales como: la igualdad de las frecuencias relativas para cada categoría, las pruebas basadas en rachas, la independencia estadística entre las categorías y la detección de patrones en la secuencia (Koller, 2018).
El campo donde más se ha avanzado en el desarrollo de pruebas de aleatoriedad es el de la evaluación de generadores de números pseudo-aleatorios (Pseudo-Random Number Generator, PRNG) utilizados en encriptación de datos (Martínez, 2018) (Gangyi, 2019). Entre los paquetes de pruebas más conocidos destacan Crypt-XS, la batería de pruebas Diehard “Intransigente” y su desarrollo posterior: el TestU01 (Shen, 2019), NIST Statistical Test Suite (Iwasaki, 2018) y Randomness Testing Toolkit (Obrátil, 2017). Algunas de las pruebas incorporadas son el test de Wald-Wolfowitz, basado en la cantidad de rachas observadas en la secuencia (Doganaksoy, 2015); el test de frecuencias monobit; la prueba de espaciamiento entre cumpleaños; la prueba de los monos, basada en la paradoja de los monos mecanógrafos; el test espectral (aplicación de la transformada discreta de Fourier), la entropía aproximada, y el test de Lempel-Ziv (Obrátil, 2017).
La alternativa que se aborda en el presente trabajo consiste en analizar el comportamiento de las distancias discretas entre eventos de una misma categoría: computar las distancias y juzgar acerca de la aleatoriedad de la muestra en base a su distribución. Para lograr este objetivo es necesario responder dos preguntas fundamentales: ¿Qué distribución teórica de probabilidades corresponde a la distribución de las distancias entre eventos iguales en una secuencia aleatoria? y ¿Qué pruebas estadísticas pueden aplicarse para determinar la correspondencia entre la distribución teórica y la observada?
Adicionalmente es de interés el estudio minucioso de los resultados que brindan las pruebas aplicadas a fin de evaluar su convergencia y robustez, detectar desviaciones en la frecuencia de errores esperados y comprobar la sensibilidad de las pruebas a diferentes fuentes de comportamiento no aleatorio.
MÉTODOS
Fundamentación teórica de la prueba de las distancias
Sea una secuencia finita de datos categóricos X, compuesta por n eventos y k categorías diferentes. Para cada categoría se define la frecuencia absoluta y frecuencia relativa como:
ni: frecuencia absoluta: cantidad de eventos de la categoría i,
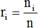: frecuencia relativa de los eventos pertenecientes a la categoría i. (1)
La secuencia categórica, una vez codificada, puede tener un aspecto como el siguiente:
ABCAABDAEBACABBCDAAABCADE …
Donde cada carácter representa un evento o estado del sistema. Los eventos son mutuamente excluyentes. La posición en que se encuentra cada carácter determina el instante de tiempo en que ocurre cada evento: 1, 2, 3, siendo este una variable discreta autoincremental.
Se define como distancia (d) entre dos eventos sucesivos de la misma categoría (xj = xj+h) la cantidad de pasos necesarios para alcanzar desde xj desde xj+h.
d = 1, 2, 3,… discreta.
d(xj, xj+h) = h; (2)
d(xj, xj+1) = 1; la distancia entre dos eventos contiguos es igual a 1.
La distancia para el primer elemento de la categoría i se define como la suma de los pasos desde el inicio de la secuencia hasta el primer xj = Ki más los pasos desde el último xj = Ki hasta el final de la secuencia.
El promedio (media aritmética) de las distancias para cada categoría es:
(3)
Tomando la frecuencia relativa para cada clase como estimador de probabilidad con que ocurre el evento Ki pueden definirse las probabilidades de obtener las distancias al próximo evento como sigue:
P(1) = ri probabilidad de que la distancia al próximo evento de la clase i sea d = 1.
P(2) = ri(1 - ri) ídem, d = 2. Resulta de aplicar la regla de multiplicación para dos eventos sucesivos: que no ocurra el evento xi en un primer momento (1 - ri) y sí ocurra en el segundo momento consecutivo de la secuencia (ri).
P(3) = ri(1 - ri)2ídem, d = 3.
P(d) = ri(1 - ri)d-1generalización. (4)
La ecuación (4) se corresponde con la distribución geométrica, con la diferencia que aquí el argumento de la función, comienza en el valor d = 1 y no en cero como generalmente se presenta esta distribución: P(x) = r (1 - r) x (NIST, 2018). Entonces puede afirmarse que, para una distribución aleatoria de los datos a lo largo de la secuencia, las distancias entre los eventos de una misma clase siguen una distribución geométrica tal como se describe en (4).
La esperanza matemática (media aritmética) y la varianza teórica esperada para esta distribución se calculan según:
(5)
(6)
Tomando las probabilidades teóricas calculadas mediante (4) como frecuencias relativas esperadas para cada distancia (lo que es válido para n lo suficientemente grande) puede estimarse la frecuencia absoluta esperada para cada distancia como el producto:
fesp(d) = ni∙p(d) (7)
Al computar en tabla de frecuencias absolutas las distancias observadas (para cada clase independientemente) en la secuencia de datos (muestra), las diferencias cuadráticas entre frecuencias observadas y esperadas se calculan como:
(8)
Siendo m la cantidad de filas en la tabla de frecuencias, el estadístico ( 2 distribuye Chi-cuadrado con m - 2 grados de libertad puesto que se ha estimado un parámetro, ri, para calcular las frecuencias esperadas. McClave & Sincich, 2018).
El p-valor se determina como en una prueba unilateral de cola derecha. La expresión: = 1 - CHISQ.DIST(χ2, m - 1, TRUE) devuelve el resultado necesario tal y como se implementa la función Chi-cuadrado en tabuladores electrónicos tipo Microsoft Excel.
Comoquiera que las distancias observadas alcanzan un valor máximo, quedarían sin computar las distancias no observadas después de esta distancia máxima (dmax), para las cuales existe una probabilidad marginal. En este caso la tabla de frecuencias debe tener en cuenta una fila adicional donde fobs = 0, el estadístico chi-cuadrado para esta última fila sería:
(10) (10)
Donde (fesp(r) corresponde a la suma de frecuencias esperadas (remanentes) para las distancias mayores que dmax, la que puede calcularse según:
(11)
De manera que el efecto de las distancias ausentes resulta en adicionar la (fesp(r) al cómputo de chi-cuadrado obtenido en (6).
Como criterio de agrupamiento se propone utilizar la expresión para calcular la suma mínima de frecuencias esperada para cada clase de la tabla de frecuencias:
(12)
Agregando la condición adicional de cota mínima absoluta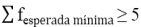 
para evitar un uso indiscriminado de la corrección de Yates (Corder & Foreman, 2016).
RESULTADOS Y DISCUSIÓN
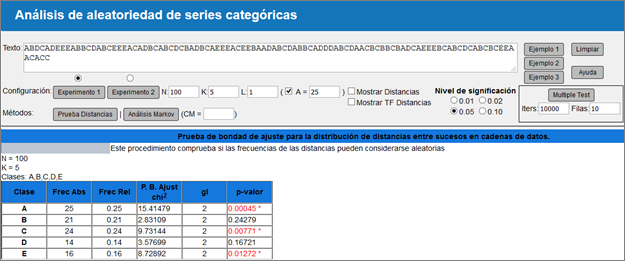
La prueba de las distancias ha sido implementada como módulo javascript para paquetes estadísticos de plataforma web el cual puede trasladarse a otros lenguajes con relativa facilidad. La interfaz gráfica de usuario fue elaborada en lenguaje HTML y contiene un panel para la entrada de datos y selección de opciones y un panel de salida de resultados. Incluye secuencias de ejemplo prediseñadas y permite generar secuencias pseudo-aleatorias bajo diferentes condiciones definidas por el usuario. Adicionalmente puede realizar simulaciones múltiples de las pruebas estadísticas incorporadas con el objetivo de evaluar su comportamiento. Figura 1
El siguiente ejemplo didáctico muestra los resultados obtenidos al aplicar la prueba de las distancias a una secuencia previamente diseñada para ilustrar diferentes clases de comportamiento de los datos.
Se desea analizar la distribución de distancias en la secuencia:
ABDCADEEEABBCDABCEEEACADBCABCDCBADBCAEEEACEEBAADABCDABBCADDDABCDAACBCBBCBADCAEEEBCABCDCABCBCEEAACACC.
Las hipótesis nula y alternativa se plantean como sigue:
H0: Las distribuciones de frecuencias de distancias observadas y esperadas son iguales, indicando que los datos se distribuyen de manera aleatoria.
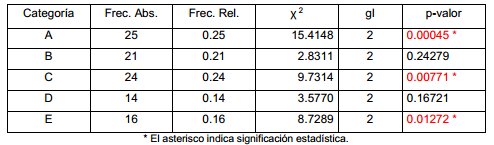
H1: Las distribuciones de frecuencias de distancias observadas y esperadas difieren significativamente, por lo tanto, los datos no están distribuidos de manera aleatoria.Tabla 1
Análisis de las distancias:
n = 100
k = 5, xi = {A, B, C, D, E}
Las distribuciones de distancias de las categorías A, C y E presentan diferencias significativas respecto al comportamiento esperado en condiciones de aleatoriedad.
El p-valor obtenido para la categoría A es significativamente menor que 0.01, esto indica que la probabilidad de que distribución de distancias de los eventos A sea aleatoria es muy pequeña, inferior al uno por ciento. La inspección detallada de los datos muestra que para la categoría A existe un marcado predominio de la distancia dA-A = 4 (8 ítems), la cual coincide con la media aritmética de las distancias entre eventos A. Esto hace sospechar que A presenta una fuerte tendencia a ocurrir cada 4 eventos de manera periódica.
En el caso de la categoría E predomina la distancia dE-E = 1 (10 ítems), indicando la tendencia de E a ocurrir en rachas de varias apariciones consecutivas. Obsérvese una regularidad en C: de 24 apariciones en la secuencia, en 14 ocasiones C es inmediatamente precedido por el evento B, lo cual es un indicio de que la secuencia tiene características de un proceso de Markov, al menos para la interacción B → C.
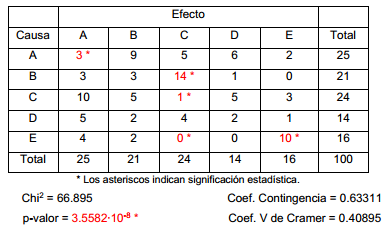
Para comprobar la propiedad markoviana en la secuencia anterior se confeccionó una tabla de contingencia para la relación causa-efecto entre todos los eventos tomados uno a continuación del otro, esta fue sometida a una prueba chi-cuadrado de independencia estadística utilizando el paquete estadístico Statgraphics Centurión (2020). Se contrasta la hipótesis nula: los valores observados para la variable Efecto (evento posterior) son independientes de la variable Causa (evento anterior) versus la hipótesis alternativa: existe relación entre la Causa y el Efecto. La Tabla 2 muestra los resultados obtenidos.
La frecuencia con que el evento A actúa como causa de sí mismo es significativamente pequeña, lo cual es coherente con el carácter periódico de A descrito anteriormente. Por el contrario, se observa una fuerte autocorrelación para el evento E como causa de sí mismo; lo que se corresponde con la tendencia observada a la aparición de rachas E consecutivos. Se revela el efecto causa-efecto para el binomio B → C, haciéndose patente la no independencia estadística entre las clases. El p-valor obtenido para la prueba de independencia estadística significativamente inferior a 001, por lo que debe rechazarse la hipótesis nula con nivel de confianza superior al 99%.
Análisis de la convergencia y robustez de la prueba
La comprobación de estas características fue realizada mediante la herramienta Múltiple Test con generación de datos aleatorios. Para secuencias generadas aleatoriamente es de esperar que la proporción de “falsos positivos” (Error Tipo I) sea aproximadamente igual al nivel de significación utilizado en la prueba (alfa). Para detectar la convergencia de la prueba se computó la desviación estándar para la proporción de casos significativos (“falsos positivos”) a medida que se incrementa la cantidad de iteraciones.
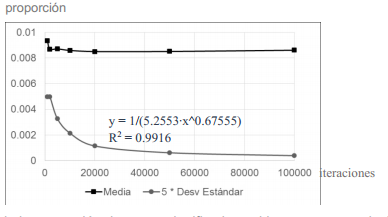
Fig. 2 Convergencia de la proporción de casos significativos al incrementarse el número de iteraciones. Simulación para n = 1000, k = 5. Significación: α = 0.01.
La curva superior en la Figura 2 representa el promedio de las proporciones y la inferior las desviaciones estándar correspondientes a cada bloque de iteraciones. La desviación estándar de la proporción de casos significativos es inversamente proporcional a la cantidad de iteraciones.
La Figura 3 analiza la robustez de la prueba. Para ni < 100 existe comportamiento errático en la proporción de casos estadísticamente afectándose la confiabilidad del test chi-cuadrado.
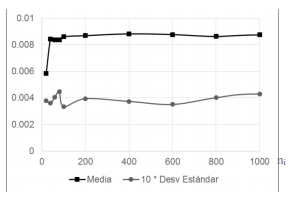
Fig. 3 Comportamiento de la proporción de casos significativos según el tamaño individual de la muestra (ni) para muestras con k = 5 categorías equiprobables (frecuencia relativa ri = 0.20). (α = 0.01)
Para de ni > 100 la tendencia la proporción de casos con significación estadística se comporta de manera estable, con fluctuaciones alrededor de 0.00873< 0.01, sin aproximación asintótica. La desviación estándar de la proporción de “falsos positivos” es significativamente inferior (1:20) al valor de la proporción, lo cual es un indicador de la robustez de la prueba. Los resultados acusan la existencia de un sesgo inherente a la prueba en el sentido de disminuir la probabilidad de cometer errores de tipo I (rechazar la hipótesis nula sobre la aleatoriedad de la secuencia cuando en realidad esta sí se cumple),
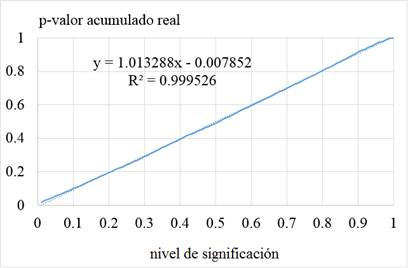
Fig. 4 Comportamiento de la proporción de casos significativos respecto al nivel de significación de la prueba de bondad de ajuste para la distribución de distancias.
El gráfico representado en la Figura 4 corresponde al comportamiento observado para eventos que ocurren con una frecuencia relativa r = 0.20 y tamaño de muestra n = 200. El comportamiento esperado indica una proporción del 1 % de casos significativos para un nivel de significación α = 0.01. Para un nivel de significación α = 0.05 se espera un 5% de casos significativos y así sucesivamente para α = 0.10, α = 0.20, hasta cubrir el intervalo (0;1). Se observan ligeras desviaciones respecto a la línea recta esperada (línea de puntos), Para las muestras estudiadas la desviación máxima resultó del 1.67 % de casos significativos observados en diferencia con la proporción de casos significativos esperados.
CONCLUSIONES
La frecuencia esperada para las distancias entre eventos de una misma clase en secuencias de datos categóricos sigue una distribución geométrica con parámetro r determinado por la frecuencia relativa de la clase en la muestra.
La prueba de bondad de ajuste para las distancias permite detectar desviaciones de la aleatoriedad respecto a la distribución longitudinal de los datos en la secuencia.
Se comprobó la sensibilidad de la prueba de aleatoriedad a comportamientos de tipo periódico, tendencia al agrupamiento de los eventos en bloques, existencia de autocorrelación y asociación entre las categorías (propiedad Markoviana).
La convergencia y robustez de la prueba son estudiadas mediante la simulación en ordenador detectándose desviaciones máximas del 1.67 % en la proporción casos significativos respecto a lo esperado que indica la existencia de sesgos inherentes al criterio de agrupamiento utilizado en la prueba chi-cuadrado.
La prueba es apropiada para su aplicación al estudio de aleatoriedad en el comportamiento de las variables involucradas en procesos y sistemas tecnológicos, el análisis de series cronológicas de naturaleza categórica, detección de procesos de Markov, análisis de textos y Big Data.
