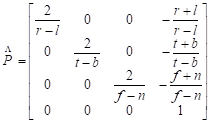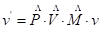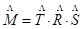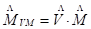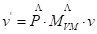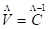Servicios personalizados
Español (pdf)
Articulo en XML
Referencias del artículo
Enviar articulo por email
Citado por SciELO 
Similares en
SciELO 
Permalink
INTRODUCCIÓN
OpenGL ES es una interfaz de programación de aplicación multiplataforma libre para renderizar gráficos 2D y 3D avanzados en sistemas integrados y móviles, incluidas consolas, teléfonos, electrodomésticos y vehículos. Consiste en un subconjunto bien definido de OpenGL de escritorio adecuado para dispositivos de bajo consumo y proporciona una interfaz flexible y potente entre el software y el hardware de aceleración de gráficos. (Khronos, 2021).
OpenGL ES 2.0 fue la primera API de gráficos móviles portátiles en exponer sombreadores o shaders sprogramables en la última generación de hardware de gráficos. Sigue siendo una API predominante en la actualidad, y sigue siendo la API de gráficos 3D más ampliamente disponible, y una opción sólida para apuntar a la gama más amplia de dispositivos del mercado (Khronos, 2021). Los diseñadores han aprovechado las bondades de los shaders, como muchos cálculos con rapidez (Linietsky, 2021) y obtener gran calidad en los gráficos que producen.
El primer fabricante de hardware en introducir shaders en sus productos fue la compañía nVidia (Charte, 2020) y fue el primer lenguaje desarrollado para crear estos programas muy similares al lenguaje ensamblador. Existe más de un lenguaje de programación de shader como el desarrollado por la empresa Microsoft, nombrado lenguaje de sombreado de alto nivel (HLSL) que puede ser usado en su tecnología Direct-X (Microsoft, 2021). De igual forma OpenGL ES cuenta con su propio lenguaje de shaders llamado GLSL (Pack, 2015) comenzándose a emplear con la versión OpenGL ES 2.0.
Los primeros experimentos para la visualización con shaders se remontan a 1993 mediante el software RenderMan (Bailey, 2009) desarrollado por la compañía Pixel y ha sido la tecnología de representación básica de esta (Techopedia, 2021). El procesamiento y visualización de grandes imágenes como las aéreas es otra de las aplicaciones de OpenGL, donde se pasan a la unidad de procesamiento gráfico (GPU) en forma de mosaicos las imágenes para crear un efecto piramidal (Painho, 2010). Uno de los mayores impulsores de estas tecnologías son los desarrolladores de la librería de software Mapnik, para la representación de imágenes de mapas, esta librería contiene interfaces para los lenguages C++ y Python (Pavlenko, 2021). OpenStreetMap OpenStreetMap proporciona datos de mapas para miles de sitios web, aplicaciones móviles y dispositivos de hardware (OpenStreetMap, 2021), el proyecto cuenta con varias librerías para renderizar mapas, sin embargo Mapnik y Osmarender son de las librerías más importantes (Rössler, 2012); la complejidad para el entendimiento y el alto nivel de dependencias con otras tecnologías de estas librerías, hacen que su estudio y la realización de una ingeniería inversa sean muy complejas, sin mencionar que aunque sus creadores afirman que son de código libre no dejan de incluir en sus archivos fuentes las licencias que se deben de cumplir para su uso. Otro de los trabajos realizados es una implementación de un motor de representación de mapas donde se muestra cómo usar técnicas, con la GPU, para alcanzar altos niveles de rendimiento (Shaojie et al., 2019). Meet TerraLens es una tecnología estadounidense-canadiense cuyo motor de representación está basado en shaders aplicado al mapeo en dos y en tres dimensiones en tiempo real (Kongsberg, 2020).
A partir del estudio realizado del surgimiento y empleo de los sombreadores por sus altas velocidades de procesamiento, se planteó como objetivo, diseñar un sistema de clases y un conjunto de métodos, que haciendo uso de shaders en OpenGL ES 2.0, funcione como una capa para la representación de datos geoespaciales, la que puede ser utilizada posteriormente para el desarrollo de sistemas de información geográfica (SIG), pues las escenas que se generan necesitan altas velocidades de renderizado (Tully, 2020).
MÉTODOS O METODOLOGÍA COMPUTACIONAL
Durante el desarrollo de la investigación fueron utilizados los siguientes métodos : análisis-síntesis, para el estudio de las fuentes bibliográficas existentes referente al tema, identificando los elementos más importantes y necesarios para dar solución al objetivo planteado; el histórico-lógico, con el fin de realizar un estudio en los antecedentes sobre el uso de OpenGL ES y los shaders en el campo de la geomática y otras ramas; el análisis documental en la consulta de literatura especializada sobre el tema y la experimentación para probar la capa de representación con información espacial real.
Se realizó un análisis teórico sobre elementos matemáticos involucrados en la transformación de coordenadas en OpenGL que sirvieron como base para la elaboración del método en la obtención de la matriz Modelo-Vista-Proyección (MVP). Con el empleo del lenguaje unificado los autores de la presente investigación modelaron a través de diagrama de clases los conceptos de representación con OpenGL ES.
Transformación de coordenadas
OpenGL usa una matriz de 4 x 4 para todas las transformaciones de visualización y modelado (Woo, 1997). Los 16 elementos de la matriz se almacenan como una matriz unidimensional en orden de columna principal (Song, 2018). OpenGL ES 2.0 no es compatible con versiones anteriores (Google, 2021), razón por la cual ninguna llamada a las funciones de transformación glOrtho y glFrustum tiene efecto sobre los vértices.
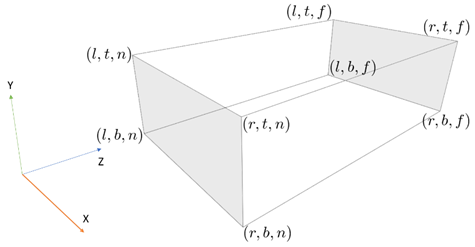
La función glOrtho describe una matriz de perspectiva que produce una proyección paralela, (Microsoft, 2021) que es la deseada, pues los gráficos a obtener en este trabajo son en dos dimensiones solamente. Esta función requiere 6 parámetros para especificar 6 planos de recorte en un espacio tridimensional; izquierda (l), derecha(r), inferior (b), superior (t), cercano(n) y lejano (f), en la Figura 1 se puede apreciar el espacio tridimensional definido por estos planos, similar a un cubo 3D (Song, 2018)
Los planos de recorte determinan cuáles o qué porción de los objetos serán visibles durante el proceso de renderización. Matemáticamente, la matriz de transformación de este tipo de proyección está definida como se muestra a continuación.
(1)
Básicamente con aplicar tres transformaciones matriciales a cada uno de estos vértices, conocidas como MVP, son suficientes para poder obtener el vértice de entrada en este espacio. Esta transformación viene dada por la expresión 2, donde: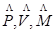 
son matrices de transformación.
(2)
Y:
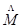: está compuesta por tres transformaciones afines, la traslación (
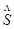), la rotación (
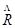) y el escalado ().
(3)
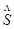A veces, la matriz de vista y la de modelo se multiplican previamente y se almacenan como una matriz de vista de modelo.
(4)
Sustituyendo la expresión 4 en la expresión 2 se obtiene que:
(5)
Si bien cada objeto tiene su propia matriz de modelo, la matriz de vista es compartida por todos los objetos de la escena, ya que todos se renderizan desde la misma cámara. Dada la matriz de modelo de la cámara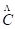 
, cada vértice 
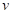puede ser transformado de su sistema de coordenada local al sistema de coordenadas del mundo y al de la cámara. La expresión 4 representa lo planteado (Santell, 2020).
(6)
Las matrices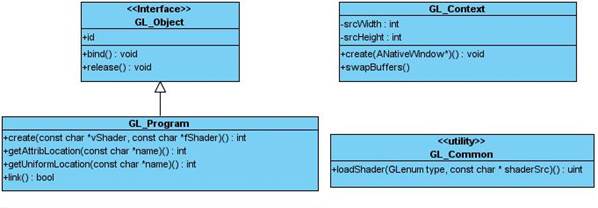 
permiten las transformaciones de las coordenadas de los vértices de los objetos al sistema de coordenadas global, o al espacio de recorte de la Figura 1. Partiendo de las expresiones matemáticas definidas, es posible el diseño de un shader que las utilice para la representación o renderización en OpenGL ES de primitivas geométricas como polilíneas.
Método de obtención de la matriz MVP
La obtención de la matriz MVP, es de crucial importancia en el procesamiento de información espacial debido a los rangos numéricos que poseen las coordenadas. La matriz debe ser calculada cada vez que cambie la extensión espacial a representar y cada aparición de una matriz de 4 x 4 es representada como mat4.
Método 1: Obtención de la matriz MVP
Entrada: Extensión espacial definida dos puntos pMin, pMax.
Salida: matriz MVP definida como mMVP.
1. mat4 mOrtho;
2. mat4 mModelView;
3. mat4 mMVP;
4. loadIdentity(out mOrtho);
5. ortho(out mOrtho, pMin.x, pMin.y, pMax.x, pMax.y);
6. loadIdentity(out mModelView);
7. translate(out mModelView, 0, 0, 0);
8. loadIdentity(out mMVP);
9. multiplyMatrix(out mMVP, mModelView, mOrtho);
Gran parte del procesamiento matemático lo realizan las funciones loadIdentity, ortho, translate y multiplyMatrix. La función loadIdentity establece todos los valores de una matriz en cero, excepto los valores de la diagonal a quienes da valor de 1. Por otra parte, ortho crea una matriz ortogonal a partir de lo planteado en la expresión 1, donde el plano de recorte en este caso se define por los valores de la extensión geográfica. La función translate ejecuta una traslación en los ejes x, y, z y finalmente el objetivo de la función multiplyMatrix es el de efectuar la multiplicación entre dos matrices en este caso mModelView y mOrtho, por tanto mMVP es el resultado de esta multiplicación matricial.
Diseño de los diagramas de clases y métodos propuestos
Clases para manejar OpenGL ES
OpenGL ES está programado con el lenguaje C, por esta razón y para agilizar el proceso de desarrollo, fueron diseñados un conjunto de clases para manejar sus conceptos de forma reutilizable. A continuación, aparece la explicación de las clases que fueron diseñadas y una breve descripción sobre su función. En la Figura 2 y Figura 3 se muestra el diseño del diagrama de clases asociado a estos.
GL_Object: es la base de todas las clases que encapsulan los conceptos de OpenGL ES y posee un solo atributo denominado id que es común en el resto de las clases. Es una interfaz y los métodos que posee, son comunes y que cada objeto de OpenGL ES deben de realizar.
GL_Program: se encarga de implementar la función de los objetos de programas, al que se le pueden adjuntar objetos shaders. La función create es la responsable de recibir como argumentos los códigos en forma de caracteres o bytes del Vertex Shader y del Fragment Shader y dar valor al atributo id. Las funciones restantes invocan a sus homólogas de OpenGL ES, pasando como primer argumento el atributo id que adquiere valor al ejecutarse la función create. El resto de las funciones invocan a sus homólogas nativas.
GL_Context: esta clase inicializa un contexto de OpenGL mediante la función create, que recibe como argumento un puntero a un objeto ANativeWindow, cuyo objeto es una interfaz brindada por el API de desarrollo nativo del sistema operativo Android, para manejar el concepto de ventana, conocido en el sistema operativo Window.
GL_Common: esta es una clase de funciones útiles. En este caso posee la función loadShader que devuelve el identificador de un objeto shader.
Método 2: Creación de un objeto GL_Program
Entrada: Código asociado al vertex sahder vs y el código asociado al fragment shader fs.
Salida: objeto GL_Program definida como prog.
1. bytes vs;
2. bytes fs;
3. GL_Program prog;
4. prog.create(vs, fs)
La función create invoca a la función nativa de OpenGL de crear un objeto de programa cuyo identificador se le asigna a la variable id de la clase base GL_OBJECT; luego carga y compila el código asociado a cada uno de los shaders mediante la función loadShader de la clase GL_Common. Si no se detectan errores, se adjuntan al programa y a partir de aquí ya puede ser linkeado a través de la función link.
Clases para efectuar la representación de polilíneas
Canvas es la principal clase de este diagrama, pues encapsula lo visto hasta este momento, en primer lugar, la matriz MVP y los objetos de programas asociados a cada tipo de geometría a representar. El atributo, mvpMatrix, es la matriz MVP deducida de la expresión 1. En este caso solo contiene un objeto del tipo GL_Program nombrado linesProgram para efectuar el dibujado de una polilínea, pero la idea es que exista un objeto de este tipo encargado de representar cada tipo de geometría, como son los casos de los polígonos y los puntos.
Color: implementa el modelo de color RGBA.
Mat4: maneja una matriz de 16 elementos o 4x4 y es usada para distintas transformaciones geométricas como escalar, rotar y trasladar.
El procedimiento drawPolyline tiene dependencias muy importantes, y se trata en primer lugar, del concepto de OpenGL Vertex Array Object, siglas que definen el primer argumento, y este a su vez depende de un objeto conocido como Vertex Buffer Object, encargado de enviar al GPU los valores asociados a las coordenadas espaciales, como se ilustra en el método 3:
Método 3: Enviar coordenadas espaciales al GPU.
Entrada: arreglo de coordenadas en el orden longitud, latitud definido como coords y la cantidad de bytes que representan estas coordenadas definida como size.
Salida: identificador del buffer de vértices vbo.
1. glGenVertexBuffer(out vbo);
2. glBindBuffer(vbo);
3.glBufferData(vbo, size, coords);
4. glBindBuffer (0);
Las funciones empleadas en este método son una representación genérica de las que brinda OpenGL ES. La función glGenVertexBuffer devuelve el manejador de un buffer de vértices creado por OpenGL y glBufferData es quien envía hacia la GPU las coordenadas espaciales. Como OpenGL es una máquina de estado se usa la función glBindBuffer para indicar que se va a activar o no un buffer para su futuro empleo. Esta técnica requiere que todas las coordenadas espaciales correspondientes a las polilíneas sean conocidas, así como la posición de la primera coordenada de cada polilínea y la cantidad de vértices que la conforman; de esta forma se aprovecha al máximo el rendimiento del GPU, ya que no hay necesidad de enviar las coordenadas por cada ciclo de rendering, sino que solo se hace una vez. Al obtener el identificador del buffer de vértices vbo se crean por cada polilínea un Vertex Array Object, tal y como describe el método 4:
Método 4: Creación de un Vertex Array Object para una polilínea.
Entrada: manejador del buffer de vértices vbo.
Salida: identificador del Vertex Array Object vao.
1. glGenVertexArray(out vao);
2. glBindVertexArray(vao);
3. glEnableVertexAttribArray(0);
4. glBindBuffer (vbo);
5. glVertexAttribPointer(0, 2,…, null);
6. glBindBuffer (0);
7. glEnableVertexAttribArray(0);
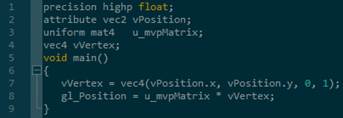
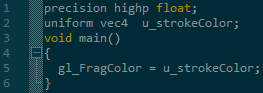
Tomando en cuenta que uno de los objetivos principales es el uso de los shaders, las imágenes 4 y 5 muestran el código asociado a dos de estos, para visualizar la polilínea. La Figura 4 representa el código del vertex sahder.
La línea 1 indica que los valores que manejará este shader son números flotantes de 16 bits. El atributo vPosition poseerá las coordenadas del punto y la variable u_mvpMatrix es la matriz transformación MVP explicada anteriormente. El shader asignará a la variable global de OpenGL ES gl_position el resultado de aplicar la matriz de transformación al punto de entrada y el fragament shader desarrollado, cuyo código se muestra en la Figura 5, modifica la variable global gl_FragColor y establece así el color con que se visualizarán estos vértices.
Estos shaders son los pasados a la función create del programa linesProgram de la clase Canvas, de forma tal que el procedimiento drawPolyline Canvas queda como se muestra a continuación:
Método 5: Dibujar polilínea.
Entrada: identificador del Vertex Array Object vao, color c, posición de la primera coordenada offset y la cantidad de vértices que la conforman nv.
1. linesProgram.use();
2. int mvpLoc = linesProgram.getUniformLocation(“u_mvpMatrix”);
3. glUniformMatrix4fv (mvpLoc, …, mvpMatrix);
4. int colorLoc = linesProgram.getUniformLocation(“u_strokeColor”);
5. glUniform4f (colorLoc, …, c.r, c.g, c.b, c.a);
6. glBindVertexArray(vao);
7. glEnableVertexAttribArray(0);
8. glDrawArray (GL_LINE_STRIP, offset, nv);
9. glBindVertexArray (0);
10. glDisableVertexAttribArray(0);
RESULTADOS Y DISCUSIÓN
Los métodos anteriores se implementaron en una aplicación de prueba con el empleo del Visual Studio 2017. Por defecto, su asistente crea una aplicación donde ésta solo referencia a la versión 1 de OpenGL ES, que no permite el trabajo con shaders y que es importante en el desarrollo de este trabajo, por lo que fue necesario establecer los ajustes pertinentes en la configuración de la aplicación, para que permitiese usar la versión 2.0 de OpenGL ES. El primer paso fue incluir en la configuración de la solución, específicamente en la parte de Linker/Input/Library Dependencies la dependencia con la librería nativa GLESv2 como se muestra en la Figura 5, la que contiene implementada las funciones de OpenGL ES 2.0.
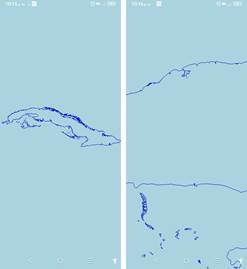
Una vez establecida la dependencia con la librería, se agregó en el archivo de encabezado de pre compilación de la aplicación, nombrado pch.h, la macro de inclusión con valor <GLES2/gl2.h>, para así poder llamar o invocar desde cualquier parte las funciones de esta extensión. La Figura 6 muestra dos capturas de pantalla realizada en un teléfono móvil que ejecutó la aplicación de prueba, con un cambio de rango en la extensión espacial a visualizar, en otros términos, con un cambio en la matriz MVP, generándose un efecto de acercamiento o lo conocido como zoom:
CONCLUSIONES
La realización de este trabajo ofrece una alternativa para el desarrollo de técnicas de representación de información geoespacial para dispositivos móviles, con una de las API gráficas más usadas en los sistemas operativos Android. Ofrece un método para la determinación de la matriz MVP, a partir de una extensión geográfica definida por un punto mínimo y uno máximo, lo que permitió transformar las coordenadas al espacio normalizado de OpenGL y así poder visualizarlas.
Para garantizar una fácil implementación se obtuvo un conjunto de clases que agruparon los conceptos específicos de OpenGL y de la representación o rendering, las que junto a los diferentes métodos expuestos constituyen una guía de desarrollo. La explicación detallada de cómo configurar una aplicación en Visual Studio 2017, con el módulo de desarrollo de aplicaciones móviles en el lenguaje C++, permitió que fuera posible utilizar la versión 2.0 de OpenGL ES y desarrollar una aplicación de prueba.
El modo de organizar las coordenadas espaciales hace que el uso de las técnicas del Vertex Buffer Object y Vertex Array Object ofrecieran su máximo nivel de rendimiento, ya que los vértices pueden pasarse solo una vez a la tarjeta de video y así evitar que por cada ciclo de rendering se envíen los datos de la memoria RAM al GPU.
