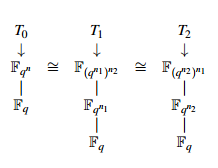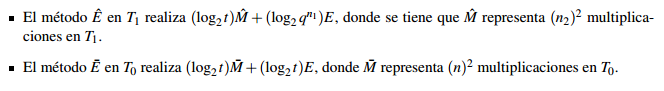Serviços customizados
Espanhol (pdf)
Artigo em XML
Referências do artigo
Enviar este artigo por email
Citado por SciELO 
Similares em
SciELO 
Permalink
INTRODUCCIÓN
Muchos de los algoritmos criptográficos, fundamentan su seguridad a partir de la dimensión del campo donde se trabaja. De esta manera, existe una tendencia a utilizar campos de gran cardinalidad para disen˜ar algorit- mos criptográficos. Así mismo, mientras que se busca poseer una seguridad considerable frente a los ataques que existen y los medios de cómputos actuales, los disen˜os tienden a utilizar operaciones más costosas desde un punto de vista computacional. Así, se hace necesario, determinar una vía que permita reducir de alguna manera el costo de las operaciones sobre campos grandes empleando una aritmética rápida. La aritmética en torres de campos finitos es muy usada para este fin, ya que poseen características esenciales para una aritmética más eficiente. Entre los primeros trabajos vinculados a la criptografía, donde se emplean las torres de campos finitos se encuentran: “Efficient Algorithms for Finite Fields, with Applications in Elliptic Curve Cryptography” ?, realizado por Baktir y Sunar en el 2003, y un an˜o más tarde “Optimal Tower Fields”Baktir and Sunar (2004) y “Optimal Tower Fields for Hyperelliptic Curve Cryptosystems”Baktir et al. (2004), donde introducen las torres de campos óptimas las cuales constituyen una clase especial de extensiones de campos óptimas introducidas por Bailey y Paar en “Optimal Extension Fields for fast arithmetics in public-key algorithms”Bailey and Paar (1998). Con el transcurso de los an˜os se han empleado en las operaciones de los emparejamientos bilineales para curva elípticas tal como lo abordan los trabajos de Kerins et al. (2005), Cor-tez (2009) y González (2010). Otros autores las han empleando en la implementación de dispositivos FPGA como Velásquez and Castan˜o (2013). También, se han implementado de forma eficiente, operaciones sobre torres de campos en las S-cajas del AES como se muestra en los trabajos Bonnecaze et al. (2013), Ueno et al. (2015), Reyhani-Masoleh et al. (2018a), Reyhani-Masoleh et al. (2018b) . Además, las torres se han emplea- do como herramientas en el disen˜o de cifradores de flujo, así lo muestran los trabajos de Fan et al. (2013), Zidaric (2014) y Zidaric et al. (2019). Los detalles sobre estos y otros trabajos en donde se emplean las torres de campos dentro de la Criptografía se pueden encontrar en Pérez Roble (2017).
Por otra parte, los polinomios primitivos son de vital importancia por su utilización en los disen˜os de algunos componentes de los criptosistemas simétricos existentes como los LFSRs (Registros de Desplazamiento con Realimentación Lineal) Golomb (1982); Mullen and Panario (2013); Delgado (2010); Peralta (2005); Fan et al. (2013); Zidaric (2014); Zidaric et al. (2019); El-Razouk et al. (2015), en cifradores en flujo, en generación de matrices MDS (Maximum Distance Separable) Junod and Vaudenay (2004); Pérez (2014); Freyre et al. (2014); Dehnavi et al. (2014); Gupta and Ray (2015); Cuellar (2017); Gupta and Pandey (2017); Mahmoodi et al. (2019) y en cifradores en bloque (AES). En el 2017, E. Madarro; Madarro (2017), Madarro and Cuellar (2021); presentó un algoritmo de generación de polinomios primitivos sobre F2 m , el cual se descompone en tres partes fundamentales: la búsqueda de los cosetos q-ciclotómicos, el cálculo del polinomio mínimo y el cálculo del polinomio reverso; siendo la segunda la de mayor complejidad ya que es en donde intervienen operaciones de multiplicación y exponenciación; debido a esto surge la necesidad de encontrar herramientas que permitan
reducir la cantidad de operaciones a realizar en dicho algoritmo. Para esto se llevó a cabo un estudio de
diferentes métodos escogiendo el empleo de las torres de campos finitos en bases normales por las ventajas que proporcionan para el cálculo. El objetivo de este trabajo es aplicar bases normales sobre torres de campos finitos en las operaciones de multiplicación y exponenciación que intervienen en el cálculo del polinomio mínimo del algoritmo propuesto por E. Madarro. Este artículo forma parte de los resultados obtenidos en la tesis de maestría Pérez Roble (2019) (Aritmética sobre Torres de Campos Finitos de característica dos, aplicada a la generación de polinomios primitivos) presentada en la Universidad de La Habana en el 2019.
MÉTODOS O METODOLOGÍA COMPUTACIONAL
En la literatura se presentan varios algoritmos para la generación de polinomios primitivos, entre los que se encuentran: “Porto, Guida y Montolivo”di Porto et al. (1992), propuesto por A. Di Porto, F. Guida y E. Montolivo en 1993; “G. Filho y D. Filho”da Silva and Lima (1993), presentado en 1993 por Joel Guilherme da Silva Filho y Dimas de Queiroz Lima Filho; “Rifa y Borrell” Rifa and Borrell (1995) de 1995 construido por J. Rifa, y J. Borrell; “FactorPower”, propuesto por Saxena y McCluskey en 2004 Saxena and MacCuskey (2004); y los algoritmos de “Shoup” Shoup (1999, 2008) presentados en 1999 y 2008, respectivamente.
En el 2017, E. Madarro Madarro (2017) presenta un algoritmo de generación de polinomios primitivos sobre f2m ; empleando como entradas: dos polinomios primitivos f y g de grados m y n respectivamente, los cuales definen las extensiones F2 m y F(2 m)n ; un elemento primitivo a del campo F q n , donde q = 2 m . El primer paso del algoritmo propuesto por Madarro, busca los cosetos líderes q-ciclotómicos módulo q n 1 asociados a los elementos del campo, que a su vez constituyen elementos primitivos descritos en Cuellar et al. (2016); Madarro and Cuellar (2016). Luego de obtenido los cosetos, se realiza el cálculo del polinomio mínimo para cada conjunto formado por los elementos αh, αhq, αhq2 , ..., αhqn−1 , siendo esta la operación más costosa
debido a la cantidad de operaciones (multiplicaciones y exponenciaciones) a realizar. Por último, se calcula su polinomio reverso, ya que este también es primitivo.
Con el fin de encontrar formas más eficientes para el cómputo de las operaciones en campos finitos, varios autores han expuestos disimiles enfoques; siendo el trabajo sobre torres de campos uno de los más llama- tivos. Las torres de campos finitos permiten reducir la cantidad de operaciones aritméticas a realizar en los subcampos contenidos en él.
Una torre sobre un campo finito F es estrictamente un conjunto de extensiones finitas de F las cuales están totalmente ordenadas por inclusión.
Otro de los aspectos considerados para reducir la cantidad de operaciones fue el tipo de base empleada en la descripción de los campos finitos y las ventajas operacionales de las mismas. El algoritmo propuesto por Madarro, trabaja los elementos descritos a través de una base polinomial sobre el campo primo, una de las más conocidas y estudiadas; no obstante se decidió analizar el mismo si se considera la representación de los elementos a través de una base normal por las ventajas de la operación de exponenciación en las mismas. Las definiciones, proposiciones y teoremas, sobre las torres de campo, las bases normales y sus operaciones se encuentran en Mullen and Panario (2013); Lidl and Niederreiter (1986); Fraleigh (2003).
es una base normal de F q n sobre F q si γ constituye un elemento normal de F q n sobre F q .
Teorema 1 (Existencia). Para cualquier campo finito K y cualquier extensión finita F de K, existe una base normal de F sobre K.
Toda base normal posee una tabla de multiplicar la cual constituye una matriz n × n, cuyas entradas son las coordenadas c i j del producto γ · γqk , donde k = 0; n − 1 en la base normal.
La operación de multiplicación entre elementos representados a través de bases normales tiende a facilitarse pues los productos entre los elementos de la base ya están definidos en la tabla de multiplicar de la base, o sea:
Sean los elementos β 1 , β 2 ∈ F q n representados de la forma:
calculando los productos γqi · γqj siendo i ≤ j se obtiene:
Las coordenadas del producto γ · γqj−i en la base normal están en la tabla de multiplicar de la base.
En el campo F q n , tomando como base normal {γ, γq,..., γqn−1 el cálculo de potencias del tipo q i , se realiza a través de la siguiente proposición:
β¯i = (b n−i , b n−i+1 , ..., b n−1 , b 0 , ..., b n−i−2 , b n−i−1 ).
Cosetos ciclotómicos y bases normales
Uno de los principales pasos del algoritmo de generación de polinomios primitivos es el cálculo de los cosetos líderes (h) q-ciclotómicos módulo q n 1 por lo que se tiene el conjunto {h, hq, hq 2 , ..., hq n−1 } a partir del cual se construyen los conjugados del elemento βh que se emplean en el cálculo del polinomio mínimo.
La forma que tienen dichos cosetos es análoga a la forma de los exponentes de los elementos de una base normal. Por lo que, si se emplea una base normal {γ, γq, γq2 , ..., γqn−1 } sobre F q n y siendo β un elemento pri- mitivo de F q n , para calcular los elementos βh, βhq, βhq2 , ..., βhqn−1 , solo es necesario calcular las coordenadas de βh en la base normal, ya que las demás potencias van a ser corrimientos de estas, por la proposición 1.
Torres de campos con bases normales
El análisis de la aritmética en las torres se realiza a través del comportamiento de esta en cada una de las extensiones que la integran, debido a que las torres varían en cuanto cantidad de extensiones y la cardinalidad de cada extensión se vuelve muy complejo la generalización de las operaciones Bonnecaze et al. (2013).
Teniendo en cuenta que todos los campos finitos, que poseen la misma cardinalidad, son isomorfos; muchos trabajos en donde se emplean estos, se apoyan en torres y se construye el campo sobre el que se desea trabajar como una extensión de algún subcampo contenido estrictamente en él y no necesariamente sobre el campo primo o sobre algún campo base como se explicó con anterioridad. A pesar de que estos campos son isomorfos, la complejidad de sus operaciones es diferente.
Las torres T 1 y T 2 son dos variantes que se pueden obtener del campo F q n/F q donde n se descompone en n 1 n 2, aunque no son las únicas ya que se pueden construir otras torres combinando las cantidad de divisores n.
El empleo de las bases normales dentro del trabajo con las torres de campos conlleva a identificar elementos normales de la torre. Además, se hace necesario, para poder implementar las operaciones, la tabla de mul- tiplicar de la base normal escogida. Como en este trabajo solo se emplearán las torres conformadas por 2 extensiones (T 1 , T 2) solo es necesario dos tablas de multiplicar de taman˜o n 1 X n 1 y n 2 X n 2 para describir los elementos en cada una de ellas, que brindan ventaja en espacio si se considera que la tabla de multiplicar del campo F q n tiene taman˜o n × n.
RESULTADOS Y DISCUSIÓN
Exponenciación
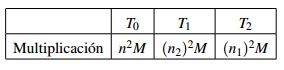
Antes de introducir el exponenciación, se analiza la multiplicación usual, la cual opera elemento a elemento. La cantidad de operaciones que realiza está relacionada directamente con la dimensión del campo donde se trabaja, en el caso de F q n se realizan n 2 operaciones. Para representar de forma más cómoda las operaciones, se denota a las multiplicaciones y exponenciaciones triviales con las letras M y E respectivamente.
La multiplicación entre elementos de las torres T 1 o T 2 se realiza de la misma manera que se indicó anterior- mente, apoyándose en sus correspondientes tablas de multiplicar, por lo que en T 1 se realizan (n 2)2 operaciones en F (q n1 )n2 y de forma análoga en T 2, (n 1)2 operaciones en F (q n2 )n1 como se muestra en la Tabla 1. Ya que esta operación se comporta de la misma manera en dichas torres, de ahora en lo adelante se hace referencia solo a T 1 y se denota como Mˆ a las multiplicaciones que se realizan en esta y M¯ a las multiplicaciones en T 0.
El exponenciación es una de las operaciones más costosas, por lo que se hace necesario emplear mejores métodos de exponenciación. Uno de estos es el clásico método de exponenciación binaria del exponente Knuth (1997), el cual emplea la expansión binaria de este utilizando log2(t) multiplicaciones y log2(t) exponenciaciones.
En este caso, se emplean las características del método anterior con algunas modificaciones a la hora de representar el exponente para realizar la operación βt , con β∈F q n . Para esto, t se descompone de la siguiente forma,
t = a 0 q 0 + a 1 q 1 + ... + a i q i + ... + a z−1 q z−1 ,
donde a i son todas las potencias de 2 menores que q, siendo q potencia de 2. Esta forma de representación está dada para aprovechar la proposición 1, en la exponenciación con bases normales.
Con este tipo de representación, una elevación a cualquier potencia t se reduce a k exponenciaciones, siendo k las potencias de 2 menores que q de la representación de t y w(t) 1 multiplicaciones, donde w(t) es el peso de Hamming del vector que representa t en base 2. Además, w(t) puede ser acotado superiormente con [log2 t|+ 1 ya que este representa la cantidad de lugares que se necesitan para representar a t en base 2 y k a su vez puede ser también acotado con log2 q.
La Tabla 2 muestra la cantidad de operaciones como máximo que se necesitan para calcular βt F q n con el método de exponenciación propuesto en bases normales (Eˆ) y el método binario en base polinomial (E¯), donde se puede apreciar la disminución de operaciones del primero frente al último.
Aplicando los métodos de exponenciación descritos anteriormente Eˆ en T 1 y E¯ en T 0 nos queda lo siguiente.
En la Tabla 3 se puede apreciar la disminución de operaciones a realizar del método Eˆ en T 1 frente a E¯ en T 0, ya que n 2 es un divisor de n y q n 1 forma parte de la descomposición del exponente t.
Torres de Campos en el cálculo de polinomio mínimo
El objetivo del algoritmo de Madarro es calcular los polinomios primitivos de grado n sobre un campo F
q
y como bien se observó las operaciones entre binomios y las potencias para hallar los conjugados se realiza con elementos de F
q
n . Para emplear las torres se asume que n se puede expresar como el producto de n
1 y n
2 lo que permite construir una torre formada por las siguientes campos extendidos: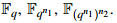 
Dado que 
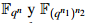poseen la misma cardinalidad, entonces se puede establecer una relación de isomorfismo entre un elemento γ F
(q
n1 )n2 y un elemento α F
q
n los cuales van a tener el mismo orden. Por tanto, el cálculo de un polinomio mínimo de grado n sobre F
q
viene dado por fórmula
Con las coordenadas del elemento γ sobre la base normal, para el cálculo de γ h, se emplea el método de exponenciación propuesto, en este caso buscando la representación de h en potencias de q n 1 para lo cual solo hay que calcular los elementos γ k, siendo k las potencias de 2 menores que q n 1 .
De manera general, para la construcción de un polinomio mínimo de grado n sobre F
q
empleando la torre T
1 con bases normales, es necesario realizar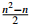 
multiplicaciones y n
1 exponenciaciones con el método propuesto E, donde cada multiplicación equivale a (n
2)2 operaciones en F
(q
n1 )n2 . Las n
1 exponenciaciones representan los elementos del primer grupo de 3 y las demás van a ser corrimientos de estas. En el siguiente ejemplo se muestra cómo se realizan las operaciones en torres de campos con bases normales a través del algoritmo de Madarro.
Ejemplo1 Se desea calcular los polinomios primitivos de grado 4 sobre el campo F4. El campo de búsqueda natural para los elementos primitivos es la extensión F44 /F4. Dicho campo es isomorfo al descrito a través de la torre F(42)2 /F42 /F4 (F (q n1 )n2 /F q n1 /F q ), un elemento primitivo de F(42)2 /F42 es W = γ, siendo γ raíz del
polinomio irreducible f (x) = x 2 + x + αβ + 1, tal que β ∈ F42 es raíz del polinomio irreducible x 2 + x + α
sobre F4 y α ∈ F4.
Dos bases normales correspondientes con las extensiones descritas son: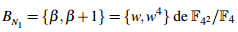 
y 
cuyas tablas de multiplicar son:
De esta forma se tiene que W tiene coordenadas (1, 0) en la base BN2 .
Como se explicó anteriormente, se hace necesario calcular las coordenadas de W elevado a las potencias 2 menores que 16, las cuales se van a emplear en todos los cálculos para la generación de los polinomios primitivos.
En este caso:
Los cosetos 4-ciclotómicos líderes primos relativos con 255 son {1, 2, 7, 11, 13, 14, 19, 22, 23, 26, 29, 31, 37,38, 41, 43, 46, 47, 53, 58, 59, 61, 62, 86, 91, 94, 103, 106, 107, 122, 127, 191} , por lo tanto h toma valores en dicha lista.
Se calcula el polinomio primitivo a partir de la sustitución en la ecuación 2 de los valores de h:
(x + W h )(x + W h4 )(x + W h16 )(x + W h4∗16 )
Para h = 19 se tiene:
(x + W 19)(x + (W 19)4)(x + (W 19)16)( x + (W 19)4∗16)
Se debe calcular las coordenadas de W 19 y (W 19)4, ya que por la proposición 1, (W 19)16 y (W 19)4∗16 son un corrimiento respectivamente de las anteriores. Al emplear el método de exponenciación propuesto:
W 19 = W 16 · W 2 · W
(W 19)4 = (W 4)16 · W 8 · W 4
Luego
De igual forma:
(W 19)4 = [αw + αw 4]v + [αw]v 16
y su corrimiento
(W 19)16 = [(α + 1)w + (α + 1)w 4]v + wv 16
(W 19)4 = [αw + αw 4]v + [αw]v 16
y su corrimiento
(W 19)4∗16 = [αw]v + [αw + αw 4]v 16
Con estos valores, el polinomio resultante es:
x 4 + αx 3 + (α + 1)x + α
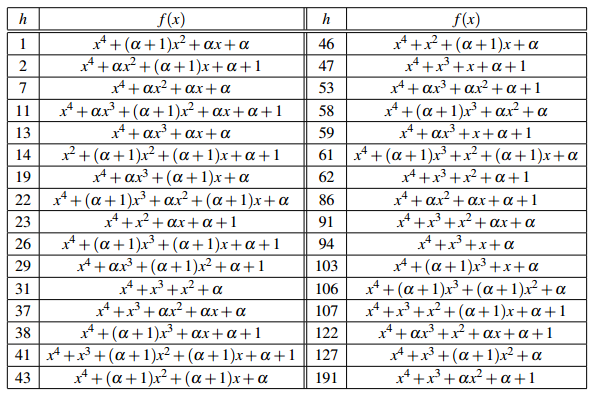
Entonces, para todos los cosetos líderes restantes se obtienen los polinomios primitivos que aparecen en Tabla 4.
Para obtener cada polinomio se realizan 6Mˆ + 2Eˆ en F(42)2 .
El método original, usando la torre T 0 con bases polinomiales realiza multiplicaciones y n exponenciaciones, donde cada multiplicación equivale a n 2 operaciones en F q n y las n exponenciaciones representan todas las raíces del polinomio resultante. Por tanto, se puede apreciar las diferencias que existe en cuanto a la cantidad de operaciones que se necesitan para resolver el problema planteado del cálculo del polinomio mínimo expuestos en la Tabla 5.
CONCLUSIONES
En este trabajo se analizaron los principales conceptos relacionadas con el uso de las torres de campos utilizando bases normales para el algoritmo de generación de polinomios primitivos y se arribó a las siguientes conclusiones:
Las Torres de Campos Finitos construidas con varias extensiones son una herramienta poderosa para lograr una aritmética más eficiente.
Se emplearon las Bases Normales por las buenas propiedades que poseen respecto al cálculo de las potencias, lo que trajo consigo la propuesta de un método de exponenciación que aprovecha estas ventajas.
La forma de los cosetos q-ciclotómicos módulo q n 1 es análoga a la forma de los exponentes de las bases normales, lo que contribuyó a disminuir la cantidad de potencias a realizar en el cálculo de las raíces del polinomio mínimo.
El empleo de torres con bases normales en la segunda operación principal del algoritmo, mostró una disminución en cuanto a la cantidad de operaciones a realizar respecto a la versión original.
Para trabajos futuros, se recomienda:
Implementar el algoritmo empleando las torres de campos con bases normales y realizar un estudio más profundo de la incidencia de estos en la complejidad general del algoritmo.
Analizar el comportamiento de las operaciones empleando otros tipos de torres.
