Original Article

Reducing the effects of muscle fatigue on upper limb myoelectric control using adaptive LDA

Roberto Díaz-Amador¹  , Miguel A. Mendoza-Reyes¹  , Julián L. Cárdenas-Barreras² 

¹Universidad Central Marta Abreu de Las Villas (UCLV), Santa Clara, Cuba

²University of New Brunswick (UNB), New Brunswick, Canada

ABSTRACT

Muscle fatigue is considered one of the main causes of sEMG changes during repetitive contractions performed for long periods of time. In the current work we are proposing and evaluating an approach in order to reduce the effects of muscle fatigue on upper limb myoelectric control using adaptive LDA. A dataset of surface EMG signals from nine subjects, including six normally-limbed and three upper limb amputees, was processed. The EMG signal was encoded using four time-domain features and four coefficients of an auto-regressive model. Adaptive and non-adaptive strategies were compared using Accuracy, False Positive Rate, Sensitivity and F1 score. Results obtained with normally-limbed subjects show that in normal scenario while muscle fatigue increases, the recognition accuracy and Sensitivity of the classifier decrease from more than 90 % to less than 58 %; False Positive Rate increases from around 9 % to 36.2 %, and F1-score decreases from 0.9 to 0.6. In contrast, parameters maintain a more stable and higher performance when adaptive LDA is evaluated. Although control in amputees shows a reduction in performance compared with normally-limbed subjects, results show a similar trend. The Wilcoxon sum rank test shows a significant increase in performance of upper limb myoelectric control tasks when adaptive LDA is used. The main limitation of this work is the need of supervision in the adaptation procedure to decide if a trial is adequate for retrain the model, making the proposed method difficult to implement in a real scenario. Future work is needed in order to obtain a parameter that serves to choose the proper trial for model retraining.

Key words: adaptive linear discriminant analysis; upper limb myoelectric control; muscle fatigue

1.-INTRODUCTION

Limb lack can have important consequences on the quality of life of an individual. Currently, there are available different prosthetic options that can help to bring back the lost limb, from simple passive and cosmetic devices to body powered devices including myoelectric controlled prostheses. Pattern recognition-based control of myoelectric prostheses has deserved great attention in research activities ^[1-5], but it has not been widely used in clinical scenarios with little progressions since the 1960’s.

According to the scientific literature, myoelectric classification for prosthetic control in real life scenarios can be made with high accuracy ^[6]. This conclusion collides with the clinical practice that shows that only a quarter of the potential patients use myoelectric prostheses ^[7]. In ^[8] authors showed that 35 % of pediatric and 23 % of adult amputees discontinues the use of their prosthetic limb, while in ^[9] around 13 % of major upper limb amputees discontinued the use of their prosthesis mainly due to poor prosthetic comfort, function and control. This reality shows the contradiction between cost of the prostheses and their actual performance to increase the quality of live. It is maybe due to the fact that research were usually done under very controlled conditions that do not take into account some factors as electrode displacements, muscular fatigue, variability of muscle contraction effort, interferences of other signals, limb positions and many other ^[10]. Some of the latest research focused on quantifying or solve particular effects caused by electrode displacements ^[11-12], variability of muscle contraction effort ^[10], interferences of other signals ^[13], and limb positions ^[14-15]. On the other hand, it is difficult to find research which have been carried out to test for the effectiveness of the sEMG-based myoelectric control when the system is affected by muscle fatigue ^[16-17].

Muscle fatigue is considered in ^[17] the major cause of sEMG changes during repetitive contractions performed for long periods of time. However, muscle fatigue changes the recruitment of motor units contributing to muscle contraction, which in turn changes the nature of any sEMG signal measured at that muscle. Sustained static isometric contractions may cause an increase in EMG signal amplitude along with a shift of the spectrum towards the low frequencies. These changes suggest that sEMG signals are time-varying due, among other factors, to muscle fatigue.

In ^[18] Park and Meek proposed a fatigue compensator preprocessor to reverse the effects of muscle fatigue on the frequency spectrum of an EMG signal. The method takes advantage of the fact that muscle fatigue affects the velocity of conduction of the muscle fibers. In their approach, the velocity of conduction is used as a fatigue measure, as well and a factor of compensation during fatigue contraction, in which the amplitude of EMG is scaled down, and the Power Spectral Density is decompressed from low frequencies. As main limitation of their work, it is worth mentioning that this approach was based in a specific single muscle movement, without considers the real situation where various muscle movements are involved. In other application, Song et al. ^[19] found that pattern recognition based systems, such as those that perform the classification using signals from a variety of EMG channels, are especially susceptible to the effects of fatigue. They proposed a fatigue compensation approach adjusting the parameters of the classifier during contraction time. The work was focused on the case of six basic movements addressed to control a powered wheelchair. Another work ^[20] proposed an alternative of a Linear Discriminant Analysis (LDA) classifier in order to adapt the parameters of the classifier to the time-varying characteristics of the sEMG signal. The proposed method provides good performance, and authors included data from clear and noisy environments, nevertheless the work was not focused in the effects of muscle fatigue, which is the main objective in the current study. Adaptability of the hand prostheses is an aspect that was recognized in ^[21] as a method that can help to improve the functionality of the prostheses. In ^[22] authors proposed a self-correcting system using LDA as movement classifier and an artificial neural network (ANN) to provide a confidence to the self-correct process. A covariate shift adaptation was evaluated in ^[23], but it is not exactly an adaptive system, but also it is a day to day retrained system. Finally, in ^[24] an incremental learning algorithm was evaluated in a scenario that includes two different day to collect the entry dataset. In ^[25-26] authors proposed a fuzzy rule based scheme to compensate the effects of muscle fatigue on EMG-based control. A set of fuzzy rules based on EMG Root Mean Square (RMS) and Mean Power Frequency (MPF) features were used to estimate weights, which correspond to the level of the muscle fatigue condition. However, this study was focused only in one Degree of Freedom (DoF) movements, considering only the flexion/extension of the elbow while subjects hold an external weight. We consider that it is not a suitable model of the daily activities that cause fatigue in amputees.

From all of the previous papers revised, we can conclude that a method that be able to reduce the effects of muscle fatigue in upper limb prostheses is mandatory in future developments and is an unsolved problem at present. We hypothesized that the solution should consider a scheme that can react to changes caused in sEMG during muscle fatigue. In this context, the current paper revisited ^[20] and we are proposing and evaluating an approach to reduce the effects of muscle fatigue on upper limb myoelectric control using adaptive LDA. Results obtained in the current research are presented and discussed in the following sessions, and shown that the adaptive approach is a tentative alternative to mitigate the effects of muscle fatigue in upper limb prosthesis control.

2.- MATERIALS AND METHODS

2.1.- EMG SIGNAL DATASET

Surface EMG signal dataset contains records from nine subjects, including six normally-limbed and three upper limb amputees. Data from the six normally-limbed subjects were collected by the authors using six wireless silver electrodes equally spaced around the dominant forearm. The electrodes were placed approximately at one third of the length of the forearm (Figure 1a) at the area of largest muscle bulk (Figure 1b). No individual muscle was directly measured but the contribution of all together. The main muscles located in this area are: flexor carpi, pronator teres, brachioradialis, extensor carpis and extensor digitorum. Data were acquired using a Trigno Wireless System (Delsys Inc., USA) ^[27] (Figure 1c) configured to work with a sampling frequency of 2.0 kHz and a 16-bit analog-to-digital converter in a range of 11 mV. Low frequency motion artifacts were reduced using a 20 Hz cutoff high-pass 3^rd order Butterworth digital filter. Power line interference (60 Hz in this case) was reduced using a notch 6^th order cascaded digital Butterworth filter. Normally-limbed subjects included three males and three females, with ages ranging from 24 to 36 years. During acquisition, normally-limbed subjects were asked to maintain the contraction of each of the eight classes of motion: wrist flexion/extension, wrist pronation/supination, hand close/open, pinch grip and no motion. Each class of motion was repeated 16 times. Muscle fatigue was induced by repeating contractions and increasing duration from 3 to 30 seconds. Each contraction was repeated 8 times with duration of 3 seconds, 4 times with duration of 10 seconds and 4 times with duration of 30 seconds. This method of inducing fatigue, tried to model the real situation in which amputees try to complete each movement.

Figure 1 MG Data acquisition configuration. a) Electrodes placed at about one third of the length of the forearm using an elastic band, b) Schematic of the electrodes around the forearm, c) Trigno WirelessElectrodes used. 

Data corresponding to the three upper limb amputees were obtained from record 3 of the Ninapro database ^[28]. As is described in ^[29], twelve Trigno Wireless electrodes and a sample frequency of 2.0 kHz were used in the acquisition process. The electrodes were placed following two strategies: four using a precise anatomical position and eight equally spaced around the dominant forearm at the height of the radio-humeral joint. In the current work we used only information from these eight electrodes to conform a dense sample similar to the data from normally-limbed subjects. The sEMG signal was filtered to reduce the 50 Hz power line interference and harmonics using a Hampel filter. Amputees, with ages of 23, 50 and 59 years old, lost their limbs in accidents and the remaining forearm were of 50%, 30% and 50% respectively. Two of them have previous experience with myoelectric prostheses.

In amputees, acquisition protocol was different compared with the normally-limbed subjects; it is described in ^[29-30] and includes 52 movements grouped in 4 exercises. Each movement was repeated 10 times, each repetition lasts five seconds with three seconds of rest. In this case, fatigue was not induced, but we selected from the database only the subjects that reported muscle fatigue during the acquisition session. In the current work, we included only movements 5,6,9,10,13 and 14 and No movement from the exercise 2. Details are presented in Figure 2.

Figure 2 Movements patterns corresponding to the three upper limb amputees obtained from the Ninapro database. (Figure is adapted from Figure 2 of ^[29]) 

The influence of the muscle fatigue and the adaptive LDA approach proposed in this work were evaluated dividing the EMG recordings in equal duration epochs. The first training set was obtained from the first epoch and the performance was evaluated using all of the eight epochs. In the adaptive approach the correct result of each new epoch classification is used to retrain the model.

2.2.- FEATURE EXTRACTION

A combination of a time-domain feature set (TD) described in ^[1] and features from a 4^th order Auto-regressive (AR) model ^[31-33] conforms the TDAR feature set used in this work. The time-domain features are considered as the baseline in myoelectric control of upper limb prostheses and provide a good representation of how amplitude and frequencies change during different contractions. The TD features used are described by Equation (1) to Equation (4).

Mean Absolute Value (MAV)

$MAV=\frac{1}{N}{\displaystyle \sum }_{i=1}^N\left|x_i\right|$ (1)

Zero-crossing (ZC)

$ZC={\displaystyle \sum }_{i=1}^{N}sgn\left(-x_i*x_{i+1}\right);sgn=\{\begin{array}{c}\mathrm{1,}x>th\\ \mathrm{0,}otherwise\end{array}$ (2)

Waveform Length (WL)

$WL={\displaystyle \sum }_{i=1}^N\left|·x_i\right|;·x_i=x_i-x_{i-1}$ (3)

Slope Sign Changes (SSC)

$SSC={\displaystyle \sum }_{i=1}^{N}sgn\left(x_{i+1}-x_i\right)*\left(x_{i+2}-x_{i+1}\right);sgn=\{\begin{array}{c}\mathrm{1,}\wedge x>th\\ \mathrm{0,}\wedge x<th\end{array}$ (4)

In Equations (1) to (4), $x_i$ represents the amplitude of the sample $i$ of EMG, $N$ is the length in samples of the analysis window, and $th$ is a threshold taken as the 5 % of the MAV on the analysis window.

The AR is a time series model of the sEMG signals that were included because provides information about spectral changes in the signal, which are important for the purpose of this work. AR features were obtained by calculating the coefficients, $A=\left[\mathrm{1,}{a}_{\left(2\right)}\mathrm{,...}{a}_{\left(K+1\right)}\right]$ , of a 4^th order (K = 4) forward linear predictor defined by ^[33]:

$x_{p \left(n\right)}= -{\displaystyle \sum }_{k=1}^K{a}_k{x}_{\left(n-k\right)}$ (5),

that minimize the sum of the squares of the errors

$Err={\displaystyle \sum }_{n=1}^N{\left(x_{\left(n\right)}-x_{p\left(n\right)}\right)}^2$ (6).

All features were calculated for time segments corresponding to rectangular windows of 200 ms, overlapped 50% ^[34]. In conclusion, each channel is described by four TD features and four AR features, and space were reduced using Principal Component Analysis. With this reduction, the 48 features from each subject are mapped into 8 features that are actually used in training and testing steps. With these 48 features computed (4 TD + 4 AR by channel), the principal component analysis is carried out in the training stage, from which a representation of 8 dimensions was obtained. Using the 8 dimension representation, the classification model of each subject is computed. In the 'test' stage, it is necessary to calculate again the 48 features and map them back to 8 dimensions following the same transformation previously obtained by PCA.

2.3.- LINEAR DISCRIMINANT ANALYSIS

Linear discriminant classifier has been frequently used in sEMG based prostheses control ^[4], ^[34-35]. It is based on Bayes classification theory, where a given observation vector $x$ , is assigned to a class $c_k$ , if the inequality in Equation 7 is satisfied:

$p\left(c_k\text{|}x\right)>p\left(c_j\text{|}x\right) \forall k\ne j$ (7)

where $p\left(c_j\text{|}x\right)$ is the probability density function for the vector within $j$ classes and $p\left(c_k\text{|}x\right)$ is the probability density function for the vector within $k$ classes. Although these posterior probabilities cannot be directly measured, they can be estimated from the a priori probabilities and the class distribution according to:

$p\left(c_k\text{|}x\right)= \frac{p\left(c_k\right)p\left(x\text{|}{c}_k\right)}{p\left(x\right)}$ (8)

where $p\left(x\text{|}{c}_k\right)$ is the probability density function for the vector within classes, $p\left(c_k\right)$ is the prior probability of the class $k$ that is usually assumed equal for all classes, $p\left(x\right)$ is the probability density function of the input space and is also a constant over all of the classes. Now, the decision referred in Equation (7) can be simplified as

$p\left(x\text{|}{c}_k\right)>p\left(x\text{|}{c}_j\right) \forall k\ne j$ (9)

If the probability density function for each class is assumed to be Gaussian, it can be defined, considering a multivariate normal distribution, as:

$p\left(x\text{|}{c}_k\right) =\frac{1}{\sqrt{2{\pi }^d\left|C\right|}}{e}^{-\frac{1}{2}{\left(x-{\mu }_k\right)}^T{C}^{-1}\left(x-{\mu }_k\right)}$ (10)

where $x$ is the vector to be classified, $d$ is the number of dimensions, ${\mu }_k$ is the mean value of the class $k$ and $C$ is the common covariance. The final decision is calculated from Equation (9). For a given training dataset, the parameters ${\mu }_k$ and $C$ are fixed and the LDA classifier is static. This means it would be difficult to keep the accuracy of the LDA classifier while the EMG signal changes over time.

2.4.- ADAPTIVE LINEAR DISCRIMINANT ANALYSIS (ALDA)

In this paper we propose an adaptive mechanism to improve the performance of LDA classifier when sEMG is affected by muscle fatigue. The proposed method can be summarized as follows: if the resulting classification of each new feature vector is correct the oldest feature vector in the training set is replaced and the classifier is retrained. Figure 3a shows the traditional classification method, while Figure 3b displays the proposed method. In Figure 3b, dashed line delimits re-training steps. Note that re-training process do not modified the feature extraction step.

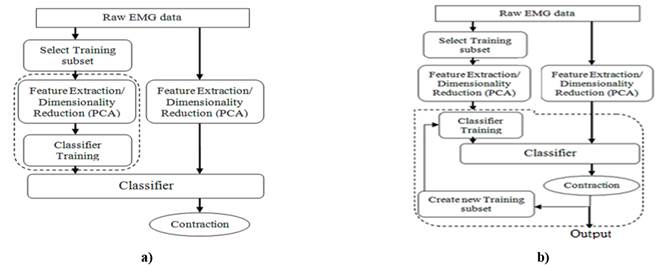
Figure 3 Flow diagram representing: a) the Traditional LDA approach. Dashed line delimits the training step. b) the Adaptive LDA approach. Dashed line delimits re-training step.  

The EMG recordings were divided in equally duration epochs of 3 seconds. The first training set was obtained from the first epochs of the first 4 repetitions of each class. In the six normally-limbed subjects the first 4 repetitions of each class correspond exactly with 3 seconds epochs. In amputees, from the first 4 repetitions of each class we extract the 3 seconds corresponding with the duration of an epoch. Summarizing, if we take into account the sampling rate, the duration of the epoch, the windows of 200 ms to calculate the features and the overlap of 50%, the total pattern to train the classifier were of 18 patterns for each class. In traditional LDA approach, no more retrain is done. In the proposed approach, the correct classification results for each new epoch are used to create a new training subset and the model is updated using the new training subset. Then, the training dataset is constantly updated, and the LDA classifier parameters are also updated tracking the changes of the signal. The new training dataset is not a completed replaced of the original training dataset, else that the 10% of the data in the first training set is kept without change in order to preserve the model stability. The new training dataset consists of a non-replaceable data subset and a subset of the correctly classified frames for each new epoch. The non-replaceable data subset is formed by the 10% with lowest entropy in the first training subset, while the correctly classified frames for each new epoch are obtained by a confidence threshold based on entropy. The confidence threshold is not discussed in the current work.

In the adaptation process itself, the new classifier parameters (mean ${\mu }_k$ and covariance $C$ ) were updated via Expectation-Maximization ^[36] as shown in ^[37]. In the Expectation step, the current probability was estimated using Equation (10), while in the Maximization step the resulting probability of the expectation is used to update the values of the mean of each classes and common covariance as in Equation (11) and Equation (12):

${\mu }_k= \frac{1}{p\left(c_k\right)N}{\displaystyle \sum }_{i=1}^{N}p\left(c_k\text{|}{x}_i\right)x_i$ (11)

$C= \frac{1}{N-1}{\displaystyle \sum }_{k=1}^K{\displaystyle \sum }_{i=1}^{N}p\left(c_k\text{|}{x}_i\right)\left(x_i-{\mu }_k\right){\left(x_i-{\mu }_k\right)}^T$ (12)

where $N$ is the last $x_i$ , and $x_i$ is weighted with the class probabilities, that, in the cases of the training dataset where the class is know, the weight for the correct class is set to 1 and for the rest of classes is set to 0.

2.5.- CLASSIFICATION PERFORMANCE

For each subject the data was divided into two subsets: training data and test data. The training data was used to train a LDA classifier, while the test data was used to evaluate the static LDA classifier and to implement and evaluate the ALDA classifier. The performance of the classifiers was measured by the offline metric classification Accuracy (Acc), False Positive Rate (FPR), Sensitivity (Se) and F1-score (F1). Expressions for these metrics are shown in Equation (13) to Equation (16):

Accuracy (Acc):

$Acc= \frac{\# Correct Decisions}{\# Total Decisions}100\%$ (13)

False Positive Rate (FPR):

$FPR=\frac{{{\displaystyle \sum }}_{i=1}^{I}F{P}_i}{{{\displaystyle \sum }}_{i=1}^I\left(F{P}_i+T{N}_i\right)}100\%$ (14)

Sensitivity (Se):

$Se=\frac{{{\displaystyle \sum }}_{i=1}^{I}T{P}_i}{{{\displaystyle \sum }}_{i=1}^I\left(T{P}_i+F{N}_i\right)}100\%$ (15)

F1-score: (F1):

$F1= \frac{Se*Pr}{Se+Pr} ;Pr=1-FPR$ (16)

In all cases I is the number of classes considered, I = 8 in this study. In Equation (14) ${\displaystyle \sum }_{i=1}^{I}F{P}_i$ represents the number of false positive when the classification task for each class is considered as a binary problem. The term ${\displaystyle \sum }_{i=1}^I\left(F{P}_i+T{N}_i\right)$ is the sum of false positives and true negatives from each class. In Equation (15) ${\displaystyle \sum }_{i=1}^{I}T{P}_i$ represents the number of true positive for each class $i$ and ${\displaystyle \sum }_{i=1}^I\left(T{P}_i+F{N}_i\right)$ is the sum of true positive and false negative for each class. Equation (16) is a simultaneous measurement of sensitivity and precision. Note that for Acc (Equation (13)), Se (Equation (15)) and F1-Score (F1) (Equation (16)) a higher value indicates a major performance, while in FPR (Equation (14)) the best performance corresponds to the lowest value. The results of each of the strategies described in this paper (non-adaptive and adaptive approach) were compared using a Friedman test and a Wilcoxon signed ranks test using a significance of p = 0.01.

3.-RESULTS AND DISCUSSION

Classification results were validated using Accuracy (Acc), False Positive Rate (FPR), True Positive Rate (Pr), Sensitivity (Se) and F1-score (F1). Validation parameters were calculated epoch by epoch in both scenarios: using Adaptive LDA and using non-adaptive LDA. Table 1 represents the True Positive Rate for each class subject by subject. An analysis of Table 1 has shown the inte-rsubject and inter-class variability. For example, in able-bodied 2, the poor class is class 3 while in able-bodied 4 the poor class is class 1. It is important to note that in general, the adaptive approach improve the True Positive Rate in both normally limbed and amputees. The class 8 shows a results close to perfect classification whit the exception of the subject 2.

Table 1 True Positive Rate for each class subject by subject comparing adaptive and no adaptive approach. Note that able-bodied subjects 8 movements while amputees 7 movements. 

Subj.	Method	Class 1	Class 2	Class 3	Class 4	Class 5	Class 6	Class 7	Class 8
Able-bodied 1	No Adapt.	90.57	77.42	95.31	83.96	76.79	91.25	80.91	88.66
	Adapt.	88.89	81.52	78.95	91.40	91.67	90.72	85.29	100.00
Able-bodied 2	No Adapt.	80.67	100.00	52.46	71.43	88.24	91.55	76.72	100.00
	Adapt.	89.52	86.05	88.42	90.43	89.69	87.76	89.58	88.66
Able-bodied 3	No Adapt.	89.36	67.47	88.78	51.20	88.10	77.48	93.33	100.00
	Adapt.	90.57	89.58	89.58	88.66	89.47	89.58	90.53	100.00
Able-bodied 4	No Adapt.	52.73	88.12	61.67	87.13	86.84	100.00	72.65	98.82
	Adapt.	73.28	87.63	89.36	89.58	89.58	100.00	87.76	100.00
Able-bodied 5	No Adapt.	90.57	88.66	88.54	92.68	62.00	88.66	83.33	100.00
	Adapt.	90.57	86.87	89.58	88.24	80.37	86.87	94.12	100.00
Able-bodied 6	No Adapt.	87.27	79.61	88.78	69.51	87.01	89.80	89.58	73.08
	Adapt.	89.72	87.18	89.58	69.51	100.00	89.58	87.76	100.00
Amp.1	No Adapt.	89.01	100.00	46.27	40.08	7.75	94.25	48.05
	Adapt.	91.49	78.57	90.79	73.47	52.69	81.08	90.43
Amp.2	No Adapt.	75.70	100.00	60.14	40.71	82.76	81.63	58.90
	Adapt.	76.19	86.08	77.98	77.61	80.00	73.55	100.00
Amp. 3	No Adapt.	68.42	57.72	67.18	85.42	69.32	79.07	100.00
	Adapt.	85.71	71.79	89.47	79.57	82.80	72.27	92.55

Figure 4 represents the mean and standard deviation of the parameters for the six normally-limbed subjects. Parameters were obtained from each of the class and combined. The solid lines represent classification results of the adaptive LDA classifier proposed in the current work, whereas the dashed lines represent classification results of the conventional LDA classifier. As shown in Figure 3, when muscle fatigue increases, the accuracy and sensitivity of the conventional LDA classifier decreases from more than 90% to less than 58% in normally-limbed subjects. Figure 3 (b) shows that False Positive Rate increases from around 9% to 36.2%. The F1-score (Figure 3 c) decreases from 0.9 to 0.6. On the other hand, the parameters of the adaptive LDA show stable and higher performance.

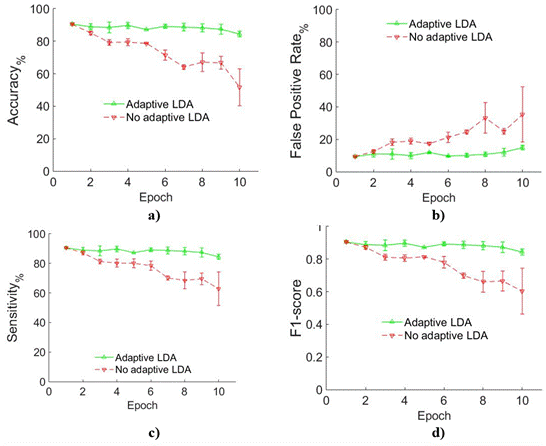
Figure 4 Comparison of Adaptive vs. Non-adaptive LDA in normally-limbed subjects a) Accuracy, b) False Positive Rate, c) Sensitivity and d) F1-score. In all cases green solid line represents Adaptive LDA while red dashed line represents Non-adaptive LDA. 

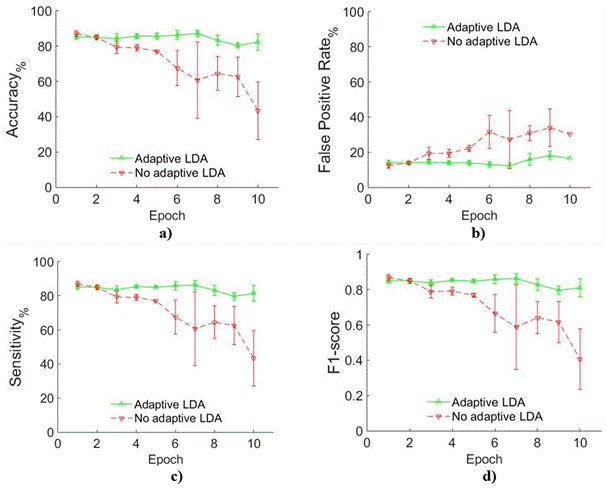
Figure 5 Adaptive vs. Non-adaptive LDA in amputees comparison a) Accuracy, b) False Positive Rate, c) Sensitivity and d) F1-score. In all cases green solid line represents Adaptive LDA while red dashed line represents Non-adaptive LDA. 

Figure 6 depicts the relative performance of Accuracy and FPR for both adaptive and non-adaptive approaches in all subjects. All Acc points located above diagonal line and all FPR points below diagonal line means that adaptive LDA performs better that non-adaptive. From Figure 5 we can observe that adaptive LDA outperforms non-adaptive LDA.

Results shows in Figure 5 and Figure 6 are compared whit results reported in ^[23] report Acc around 90 % in normally limbed subjects and 80 % in amputees. It is important appoint that in ^[23] , although authors consider factors that can change EMG patterns in time, they do not consider in particular muscle fatigue. In ^[22] , the Acc results reported are close to 100 % but muscle fatigue was not consider because data acquisition protocol include sufficient pauses between repetition to prevent fatigue. Comparing with it, the current paper presents a solution in the state of the art in myoelectric control.

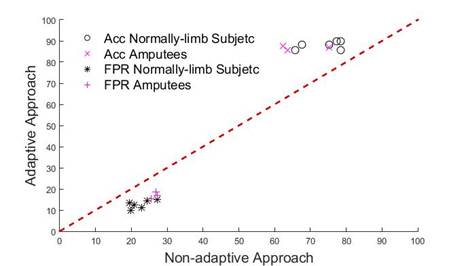
Figure 6 Comparison of Adaptive and Non-Adaptive classifiers based on Accuracy (Acc) and False Positive Rate (FPR) in both normally limbed subjects and amputees. Black Circles and purple Crosses represent Acc for normally limbed subjects and amputees respectively. All points above diagonal (line y = x) mean that in all cases Acc increases when adaptive LDA is used. Black asterisks and purple plus sings represent FPR in normally limb subjects and amputees. All points below diagonal mean that adaptive approach (y-axis) performs better that non-adaptive approach (x-axis). 

A graphical example of how much the proposed adaptive approach increases the performance of myoelectric pattern classification is shown in Figure 7. The data belong to the normally-limbed subject 6. The blue points represent the expected class for each frame, the green points represent the correctly classified frames and the red points represent misclassifications. Figure 7a) represents results from non-adaptive method while Figure 7b) shows results from the adaptive method.

Figure 7 Graphical example of how Adaptive LDA show in (b), improves the correct classification rate compared to Non-Adaptive LDA show in (a). In both, (b) and (b) red points represent misclassification cases and green points represent correct classification cases. Blue points represent the expected response. Data belong to the normally-limbed subject 6. 

For all parameters: Acc, FPR, Se and F1 score, the Wilcoxon signed ranks test shows a significant increase in performance of upper limb myoelectric control tasks when adaptive LDA is used. Details are presented in Figure 8.

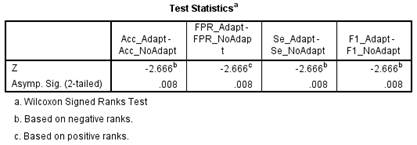
Figure 8 Wilcoxon signed ranks test showing significant different between non-adaptive LDA and adaptive LDA. 

From Figure 8, all the parameters used to compare the non-adaptive LDA and adaptive LDA proposed in this paper show significant differences with $p\_value=0.008$ . This value is less than 0.01, which is a confidence level of 99 %.

6.-CONCLUSIONS

Muscle fatigue is considered the major cause of sEMG changes during repetitive contractions performed for long periods of time. In this paper we focused on reducing the effects of muscle fatigue on upper limb myoelectric control using adaptive LDA. The proposed method is based on retraining the classifier using a new set formed by replacing 90 % of the oldest feature vector in the training set. Results show that when muscle fatigue increases, the recognition accuracy and sensitivity of the non-adaptive LDA classifier decreases from more than 90% to less than 58% in normally-limbed subjects, in the same situation False Positive Rate increases from around 9% to 36.2% and the F1-score decreases from 0.9 to 0.6. These parameters showed a more stable behavior and higher performance when adaptive LDA was evaluated. Although the overall results on amputees reveal a reduction of the performance compared to normally-limbed subjects, results show a similar trend. The Wilcoxon sum rank test shows a significant increase in performance of upper limb myoelectric control tasks when adaptive LDA is used with a confidence level of 99 %. In order to achieve a practical implementation of the proposed adaptive algorithm it is necessary a parameter that can be used to decide if certain trial is adequate for retraining the model. In addition, a future study should include the analysis of the performance in real-time conditions. These findings could help to reduce the current gap between scientific research and clinical practice in the field of EMG pattern recognition.

REFERENCES

1.  Hudgins B., Parker P.A., Scott R.N. A new strategy for multifunction myoelectric control. IEEE Trans. Biomed. Eng. 1993; 40(1).

2.  Englehart K., Hudgins B.. A robust, real-time control scheme for multifunction myoelectric control. IEEE Trans. Biomed. Eng. 2003; 50(7):848-854.

3.  Hargrove L., Losier Y., Lock B., Englehart K., Hudgin K, A Real-Time Pattern Recognition Based Myoelectric Control Usability Study Implemented in Virtual Environment. 29th Annual International Conference of the IEEE EMBS, Lyon, France. 2007; p. 4842-4845.

4.  Scheme E., Hudgins B., Englehart K.. Confidence Based Rejection for Improved Pattern Recognition Myoelectric Control. IEEE Trans. Biomed. Eng. 2013; (99).

5.  Kuiken T. A., Miller L. A. Turner K., Hargrove L. A comparison of pattern recognition control and direct control of a multiple degreedegree-of-freedom transradial prosthesis. IEEE J. Transl. Eng. Heal. Med. 2016.

6.  Amsuss S, Goebel P., Graimann P., Farina D. A Multi-Class Proportional Myocontrol Algorithm for Upper Limb Prosthesis Control?: Validation in Real-Life Scenarios on Amputees. 2014; 4320: 1-11.

7.  Geethanjali P. Myoelectric control of prosthetic hands?: state-of-the-art review. Med. Devices Evid. Res. 2016; (9): 247-255.

8.  Biddiss E., Beaton D., and Chau T.. Consumer desing priorities for upper limb prosthetics. Disabil Rehabil Assist Technol. 2007; 2: 346-357.

9.  Ostlie K. , Lesjo I. ,Franklin R. , Garfelt B. ,Skjeldal O., Magnus P. Prosthesis rejection in acquired major upper-limb amputees: a population-based survey. Disabil Rehabil Assist Technol. 2012; 7: 294-303.

10.  Scheme E. and Englehart K. Electromyogram pattern recognition for control of powered upper-limb prostheses: State of the art and challenges for clinical use. J. Rehabil. Res. Dev. 2011; 48(6): 643-660.

11.  Hargrove L., Englehart K., Hudgins B. The effect of electrode displacements on pattern recognition based myoelectric control. Annual International Conference of the IEEE Engineering in Medicine and Biology Society. 2006.

12.  Hargrove L, Englehart K, Hudgins B. A training strategy to reduce classification degradation due to electrode displacements in pattern recognition recognition based myoelectric control. Biomed Signal Process Control. 2008; 3, (2): 175-80.

13.  Hargrove L., Zhou P., Englehart K., Kuiken T.A. The Effect of ECG Interference on Pattern-Recognition-Based Myoelectric Control for Targeted Muscle Reinnervated Patients. IEEE Trans. Biomed. Eng. 2009; 56 (9): 2197-2201.

14.  Fougner A., Scheme E., Chan AD.C., Englehart K., Stavdahl Ø.. Resolving the Limb Position Effect in Myoelectric Pattern Recognition. IEEE Trans. Neural Syst. Rehabil. Eng. 2011; 19 (6): 644-651.

15.  Radmand A., Scheme E., Englehart K. A Characterization of the Effect of Limb Position on EMG Features to Guide the Development of Effective Prosthetic Control Schemes. 2014: 662-667.

16.  Lalitharatne T.D., Hayashi Y., Teramoto K., Kiguchi K. A Study on effects of Muscle fatigue on EMG-based Control for Human Upper-Limb Power-Assist. IEEE 6th International Conference on Information and Automation for Sustainability. 2012: 124-128.

17.  Barszap A., Skavhaug I., Joshi S.. Effects of muscle fatigue on the usability of a myoelectric human-computer interface. Hum. Mov. Sci. 2016; 49: 225-238.

18.  Park, E., Meek, S. Fatigue compensation of the electromyographic signal for prosthetic control and force estimation. IEEE Trans. Biomed. Eng. 1993; 40: 1019-1023.

19.  Song, J., Jung, J., Lee, S., Bien, Z. Robust EMG pattern recognition to muscular fatigue effect for powered wheelchair control. J. Intell. Fuzzy Syst. 2009; 20: 3-12.

20.  Zhang H., Zhao Y., Yao F., Lisheng Xu, Pen Shang, and Guanglin Li. An Adaptation strategy of using LDA classifier for EMG pattern recognition. 35th Annual International Conference of the IEEE EMBS, Osaka, Japan, 2013.

21.  Villarejo-Mayor J., Delisle-Rodriguez D. Towards a better adaptability of hand prostheses to improve its acceptance by amputees. Int. J. Biosens. Bioelectron. 2018; 4(2): 74-75.

22.  Amsuss S., Goebel P., Jiang N., Braimann B, Paredes L., Farina D. Self-correcting pattern recognition system of surface EMG signals for upper limb prosthesis control. IEEE Trans. Biomed. Eng. 2014; 61(4): 1167-1176.

23.  Vidovic M., Hwang H., Amsuss S., Hahne J., Farina D., Muller KR.. Improving the robustness of myoelectric pattern recognition for upper limb prostheses by covariate shift adaptation. IEEE Trans. Neural Syst. Rehabil. Eng. 2015; 24(9): 1-10.

24.  Gijsberts A., Bohra R., Sierra-González D., Werner A., Nowak M., Caputo B. et al. Stable myoelectric control of hand prosthesis using non-linear incrmental learning. Front. Neurorobotics. 2014; 8: 8.

25.  Lalitharatne T., Hayashi Y., Teramoto K., Kiguchi K. Compensation of the effects of muscle fatigue on EMG-based control using Fuzzy Rules Based Scheme. 35th Annual International Conference of the IEEE EMBS, Ossaka, Japan, 2013; p. 6949-6952.

26.  Lalitharatne T., Teramoto K., Hayashi Y., Nanayakkara T., Kiguchi K., Evaluation of Fuzzy-Neuro modifiers for compensation of the effects of muscle fatigue on EMG-based control to be used in upper-limb power assist exoskeletons. J. Adv. Mech. Desing Syst. Manuf. 2013; 7(4): 736-751.

27.  Delsys. Trigno Wireless System: User's Guide. Delsys Incorporated. 2013.

28.  Atzori M., Muller H. The Ninapro database: A resourse for sEMG naturally controlled robotic hand prosthetics. Proceedings of 37th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Milan, Italia. 2015; p. 7151-7154.

29.  Atzori M., Gijsberts A., Castellini C., Caputo B., Hager A., Elsig S et al. Electromyography data for non-invasive naturally-controlled robotic hand prostheses. Sci. Data. 2014; 1.

30.  Atzori M., Gijsberts A., Heynen S., Hager A., Deriaz O., van der Smagt P. et al. Building tha NINAPRO database: A resourse for the Biorobotics Community. 4th IEEE RAS & EMBS International Conference on Biomedical Robotics and Biomechatronics (BioRob). 2012.

31.  Graupe D., Cline W.. Functional Separation EMG Signal via ARMA identification methods for prosthesis control purposes. IEEE Trans Syst. Man Cybern. 1975; 5: 252-259.

32.  Doershuk P., Gustafson D. Upper extremity limb function discrimination using EMG signal analysis. IEEE Trans Biomed Eng. 1983; 30: 18-28.

33.  Phinyomark A., Phupattaranond P., Limsakul C. Feature Reduction and Selection for EMG signal Classification. Expert Syst. Appl. 2012; 39(8): 7420-7431.

34.  Wang N., Lao K., Zhang X.. Desing and Myoelectric Control of an Anthropomorphic Prosthetic Hand. J. Bionic Eng. 2017; 14: 47-59.

35.  Young A., Smith L., Rouse E., Hargrove L. Classification of Simultaneous Movements Using Surface EMG Pattern Recognition. IEEE Trans. Biomed. Eng. 2013; 60(5): 1250-1258.

36.  Roth V., Steinhage V. Nonlinear Discriminant Analysis Using Kernel Functions, NIPS, 1999; 568-574.

37.  Blumberg J., Rickert J., Waldert S., Schulze-Bonhage A., Aertsen A., and Mehring C., Adaptive Classification for Brien Computer Interfaces, 29th Annual International Conference of the IEEE EMBS, Lyon, France. 2007.

Received: December 15, 2017; Accepted: November 15, 2018

Roberto Díaz-Amador, , Engineering, Master in Signal and Systems, professor of Universidad Central Marta Abreu de Las Villas (UCLV), Santa Clara, Cuba. E-mail: [e-mail]

Miguel A. Mendoza-Reyes, Engineering, PhD., Titular Professor of Universidad Central Marta Abreu de Las Villas (UCLV), Santa Clara, Cuba. E-mail: [e-mail]

Julián L. Cárdenas-Barreras, Engineering, PhD., University of New Brunswick (UNB), New Brunswick, Canada, Cuba. Email: [e-mail]