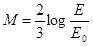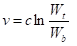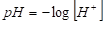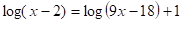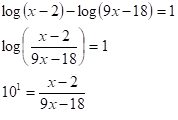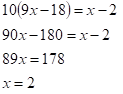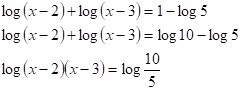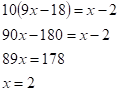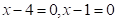Introducción
La enseñanza preuniversitaria, tiene la misión de lograr una cultura general integral donde el proceso de enseñanza aprendizaje es su principal vía, por lo que preparar a los estudiantes desde los contenidos de las asignaturas, específicamente los de Matemática les permite una mejor preparación en los estudios del nivel superior por todas las operaciones lógicas del pensamiento que desarrolla y como resultado un éxito futuro en su profesión. Un acertado criterio, ampliamente generalizado es el que enuncia que fomentan el pensamiento lógico, la resolución de problemas y la toma de decisiones informadas, habilidades esenciales para la vida cotidiana y el éxito profesional (Moreno et al., 2023).
La enseñanza de la Matemática tiene como objetivo esencial la comprensión por parte de los estudiantes de sus contenidos que les va a permitir el desarrollo de habilidades y la obtención de nuevos conocimientos a partir de los previos de grados anteriores.
Para Díaz et al. (2014):
Las dificultades de aprendizaje en Matemáticas son aquellas que afectan al desarrollo de las habilidades relacionadas con las matemáticas. Para ser diagnosticadas como tal, deben afectar al rendimiento escolar, así como generar problemas en lo que a la adaptación social, personal, escolar, familiar, laboral o comunitaria se refiere. (p.2).
Se requiere que los profesores que impartan la asignatura en este nivel de enseñanza sean capaces de dirigir el proceso de enseñanza-aprendizaje de manera creativa y faciliten la interacción ya que los estudiantes aprenden más eficazmente cuando lo hacen de forma cooperativa (Tigse, 2019), esto posibilita que el egresado obtenga los conocimientos necesarios y desarrollen las habilidades que necesitarán para enfrentar con éxito los contenidos matemáticos en otros niveles educativos, así como para su aplicación durante toda la vida.
Para González (2022) la enseñanza de la Matemática, para la nación cubana, descansa en sólidas bases científicas, con una marcada orientación hacia el desarrollo de la personalidad de los alumnos y con la aspiración de lograr una enseñanza desarrolladora, sin embargo la autora, afirma que ¨se aprecia un cierto consenso en la idea de que el fracaso o el éxito de los estudiantes en las Pruebas de Ingreso a la Educación Superior dependen, fundamentalmente de la calidad del desempeño de los docentes¨(p.2)
El aprendizaje implica necesariamente rupturas cognitivas, acomodaciones, cambio de modelos implícitos (concepciones), de lenguajes, de sistemas cognitivos. No obstante, algunas ideas resisten y persisten, expresan Caronía et al. (2014). Visto desde tal perspectiva el análisis del logro o fracaso en matemáticas, demuestra que este es un fenómeno multifactorial, que tiene muchas veces relaciones de interacción e interdependencia mutua en las que se pueden determinar algunas variables que pueden relacionarse de forma significativa con los aprendizajes o bien pueden predecir el fracaso o dificultades en el aprendizaje matemático escolar, entre las que se destacan la relación entre las de naturaleza cognitivo-afectivas y el nivel de logro alcanzado por los estudiantes en el proceso de enseñanza aprendizaje de los contenidos matemáticos (Gamal Cerda et al., 2017).
Por otro lado, Aliaga et al. (2015) consideran que es necesario por los docentes encargados de esta preparación tener dominio en primer lugar del diagnóstico de cada uno de sus estudiantes, además prestarle por las autoridades correspondientes la atención y preparación de los docentes encargados de desarrollar este programa en cada uno de los centros. Es por ello importante poner énfasis en las diversas formas en las que se presenta el contenido, así como el nivel de desarrollo alcanzado por cada uno de los estudiantes, lo que constituye elemento de motivación por el estudio de la asignatura y el logro de mayores niveles de aprendizaje. La elaboración de las tareas en cada una de las clases debe ir direccionada a este fin, o sea al establecimiento de las diferentes formas en las que se puede presentar el contenido y a los niveles de desarrollo alcanzados por cada uno de los estudiantes.
La atención a las diferencias individuales tomando como centro el trabajo preventivo y la variedad de formas en las que se pueden presentar las ecuaciones logarítmicas en las clases de Matemática juega un papel decisivo en el logro de los objetivos que se proponen en el preuniversitario, dadas sus posibilidades y potencialidades.
Sin embargo, el proceso de enseñanza aprendizaje de la Matemática del preuniversitario muestra dificultades en el contenido relacionado con las ecuaciones logarítmicas en el que se manifiesta desinterés por aprender y desmotivación por el aprendizaje, generando bajo rendimiento académico, constatado en los resultados de los exámenes en la enseñanza preuniversitaria, en los exámenes de preparación para la prueba de ingreso que se realizan en esta enseñanza y los resultados de los exámenes de ingreso en los elementos relacionados con las ecuaciones logarítmicas.
El artículo está dirigido a presentar un procedimiento para la promoción del aprendizaje de las ecuaciones logarítmicas en la enseñanza preuniversitaria desarrollado entre el 2020 y 2024, en el IPU ¨Federico Engels¨ de Pinar del Río.
Materiales y métodos
En el contexto del estudio realizado en el IPU "Federico Engels" de Pinar del Río, se aplicó un diagnóstico educativo a 80 estudiantes de 11º grado al inicio del curso escolar 2022-2023 y durante el transcurso de la unidad didáctica sobre FUNCIONES LOGARÍTMICAS Y EXPONENCIALES. El objetivo principal fue constatar el nivel de desarrollo alcanzado por los estudiantes en estos contenidos específicos.
Como método teórico fundamental el histórico-lógico permitió el análisis de los principales referentes acerca del proceso de resolución de las ecuaciones logarítmicas, con énfasis en las dificultades que poseen los estudiantes en cuanto al contenido precedente y la incidencia en el proceso de solución de dichas ecuaciones.
Se utilizaron los siguientes métodos empíricos:
Análisis de Documentos: Se revisaron los registros académicos, evaluaciones previas y materiales relacionados con las funciones logarítmicas y exponenciales. Esto permitió obtener información sobre el desempeño previo de los estudiantes en estos temas.
Observación: Durante las clases de la unidad didáctica, se realizaron observaciones para evaluar cómo los estudiantes interactuaban con los conceptos de funciones logarítmicas y exponenciales. Se prestaron especial atención a su participación, comprensión y aplicación de los contenidos.
Entrevistas: Se llevaron a cabo a los estudiantes para indagar sobre sus percepciones, dificultades y estrategias de aprendizaje en relación con las ecuaciones logarítmicas.
Resultados
El análisis de los principales referentes teóricos acerca de la influencia que ejerce la atención diferenciada en el proceso de resolución de las ecuaciones logarítmicas con énfasis en la prevención de las dificultades que poseen los estudiantes en cuanto al contenido precedente con alta incidencia en el proceso de solución de dichas ecuaciones, permitió la determinación de los elementos del conocimiento matemático de grados anteriores y de unidades didácticas anteriores al contenido relacionado con las ecuaciones logarítmicas en 11no grado, con una elevada incidencia en el proceso de solución de este tipo de ecuaciones y que a continuación se relacionan:
Proceso de solución de ecuaciones lineales, cuadráticas, fraccionarias, trigonométricas, irracionales.
Propiedades de las potencias, propiedades de los radicales, monotonía de la logaritmación, propiedades de los logaritmos.
Definición de logaritmo de un número real, base y argumento de un logaritmo, conjunto solución de una ecuación, dominio básico de una ecuación, transformaciones equivalentes, ecuaciones equivalentes.
El diagnóstico educativo, por su parte, proporcionó una visión integral del nivel de preparación de los estudiantes en funciones logarítmicas y exponenciales, lo que ayudó a orientar las estrategias pedagógicas y a diseñar intervenciones específicas para mejorar su comprensión y dominio en este importante contenido matemático.
Procedimiento para la promoción del aprendizaje de las ecuaciones logarítmicas en la enseñanza preuniversitaria
En cada una de las clases se orientaron ejercicios de estudio independiente de manera individualizada con cada contenido diagnosticado con dificultades el cual permitió trabajar de manera preventiva sobre estos contenidos y evitar así que estos se manifiesten de manera negativa en la solución de las ecuaciones logarítmicas. En la primera clase relativa a las ecuaciones logarítmicas, se les comunicó sobre la aplicación práctica de contenidos siguientes:
En 1935, el sismólogo norteamericano Charles Richter desarrolló una escala logarítmica que lleva su nombre y se usa ampliamente para calcular la magnitud de la intensidad de un terremoto mediante la ecuación:
Donde E es la energía liberada por el terremoto, medida en joules, y E
0
es la energía liberada por un terremoto de muy leve intensidad que se ha estandarizado como: 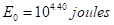
La teoría de vuelo de un cohete se utiliza en matemáticas y física avanzada para mostrar que la velocidad  de un cohete al apagarse (cuando se agota el combustible) está dada por
de un cohete al apagarse (cuando se agota el combustible) está dada por
donde c es la velocidad de escape del motor, W i es el peso de partida (el combustible, la estructura y la carga útil), y W b es el peso consumido (la estructura y la carga útil)
La concentración del ión de hidrógeno de una sustancia se relaciona con su acidez y basicidad. Debido a que las concentraciones del ión de hidrógeno varían en un rango muy amplio, se usa una escala de pH comprimida, que se define:
donde [H + ] es la concentración del ión de hidrógeno, en moles por litro.
Como se puede puntualizar, cada uno de los fenómenos abordados se resolvieron usando logaritmos comunes y naturales.
Posteriormente se les brindó el procedimiento a seguir para resolver ecuaciones logarítmicas en sus dos variantes analíticas.
Variante 1:
Obtener todos los logaritmos con la misma base
Transponer todos los logaritmos para un miembro y los términos independientes para el otro.
Obtener solo un logaritmo aplicando propiedades.
Aplicar definición de logaritmo
Resolver la ecuación que se origina
Realizar la comprobación
Expresar la solución.
Para la comprensión de este proceder metodológico se les propuso analizar el siguiente ejemplo
Resolver la siguiente ecuación
Como se observa todos los logaritmos que intervienen poseen la misma base. Se transponen todos los logaritmos hacia el miembro izquierdo de la ecuación obteniendo:
A la ecuación obtenida se le pueden realizar las siguientes transformaciones:
Por lo que la posible solución de la ecuación es x=2
Comprobando se obtiene que x=2 no pertenece al dominio de definición de la ecuación inicial por lo que la posible solución no constituye solución de la ecuación, luego S=S.
Posteriormente se les propuso a los estudiantes la variante 2 para resolver una ecuación logarítmica
Variante 2 Reducción de la ecuación a la forma 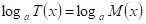 :
:
Obtener solo un logaritmo en cada miembro de la ecuación aplicando propiedades, con la característica que posean la misma base.
Igualar los argumentos.
Resolver la ecuación que se origina.
Realizar la comprobación
Expresar la solución.
Una vez que se propuso la segunda variante se procedió a su ejemplificación
Resolver la siguiente ecuación
Igualando los argumentos se obtiene la siguiente ecuación
De donde se tiene que x=4, x=1, son las posibles soluciones de la ecuación dada. Se realizó la comprobación.
La posible solución x=1, no es solución de la ecuación pues no pertenece al dominio de definición de la ecuación.
Todo lo contrario, pasa con x=4, que si es solución pues este si pertenece al dominio de definición de la ecuación.
Para la investigación se tuvieron en cuenta diferentes procedimientos utilizados por autores que han estudiado la resolución de ecuaciones logarítmicas en la enseñanza preuniversitaria, las diferentes variantes posibles para su solución y las acciones a seguir por parte del profesor en cada una de esas variantes.
Con el grupo de 80 estudiantes del IPU ¨Federico Engels¨ de Pinar del Río seleccionados que implementó durante el curso escolar 2023 el procedimiento. Se realizó un análisis sobre los resultados alcanzados en el examen final de la asignatura, en el contenido relacionado con las ecuaciones logarítmicas, en cuanto a la nota media y se compararon los resultados con los de otros estudiantes del año no sujetos de la investigación, así como con resultados de otros estudiantes en años anteriores.
Adicionalmente se llevó a cabo una comparación entre los resultados obtenidos en el examen de preparación realizado por parte de la Dirección Provincial de Educación, para contrastar el nivel alcanzado para enfrentar el examen de ingreso a la universidad, con los obtenidos en este tipo de comprobación de los cursos 2020 al 2023).
Finalmente se estableció la comparación entre los resultados obtenidos en el examen final y examen de preparación en el curso 2022-2023 con relación al examen de ingreso del 2020, año donde se evaluó este contenido, para corroborar la influencia del procedimiento con énfasis en la prevención de las dificultades con las ecuaciones logarítmicas.
Los resultados obtenidos respecto a la nota promedio en base a 20 puntos en la pregunta evaluada en examen final, relacionada con las ecuaciones logarítmicas durante tres cursos consecutivos fueron las siguientes:
Tabla 1 - Comparación de los resultados correspondientes a la nota promedio (2019-2022)
| Curso 2019-2020 | Curso 2020-2021 | Curso 2021-2022 | |
|---|---|---|---|
| Nota media | 14.5 | 13.8 | 13.5 |
La nota promedio en base a 20 puntos en esta temática de los 80 estudiantes en el curso 2022-2023 fue de 18.7, superior a lo obtenido en los anteriores (Tabla 1.) mientras que el resto de los estudiantes del grado 11no del IPU ¨Federico Engels¨ de Pinar del Río que no fueron objeto de esta investigación obtuvieron una nota promedio de 13.3 puntos, muy similar al comportamiento de cursos anteriores.
En la tabla 2. se muestran los resultados alcanzados en los exámenes de preparación para el examen de ingreso a la educación superior en la provincia Pinar del Río durante los cursos 2019-2020, 2020-2021, 2021-2022, y los resultados obtenidos en el curso 2022-2023 donde se desarrolló la investigación, en el objetivo relacionado con las ecuaciones logarítmicas.
Tabla 2 - Comparación de los resultados correspondientes a la nota media (2019-2022)
| 2019-2020 | 2020-2021 | 2021-2022 | 2022-2023 | |
|---|---|---|---|---|
| Nota media | 13.3 | 14.1 | 13.7 | 18.6 |
Por último, la Tabla 3. Muestra la comparación respecto a la nota media entre el examen final, examen de preparación para el examen de ingreso propuesta por la dirección provincial de educación, en el curso 2022-2023 y la nota media alcanzada en el examen de ingreso en el año 2020 en el contenido relacionado con las ecuaciones logarítmicas.
Discusión
De manera general los resultados permitieron constatar que, si el proceso de enseñanza aprendizaje de las ecuaciones logarítmicas en 11no grado se desarrolla con énfasis en la prevención de las dificultades en el futuro desempeño, de modo que se potencie un proceso de atención diferenciada más eficiente, se logran niveles cualitativamente superiores de aprendizaje.
Todo lo anterior permite entender que, un importante elemento para promover la motivación por el aprendizaje de estos contenidos en este nivel de enseñanza lo constituyen la orientación de trabajos investigativos y trabajos prácticos, exposiciones de aspectos históricos y del desarrollo de la Matemática, concursos de conocimientos, la utilización de asistentes matemáticos, la celebración de conferencias y conversatorios con profesores y especialistas, el análisis de los resultados históricos de estos contenidos en cursos anteriores en los exámenes de las asignaturas y exámenes de ingreso a la educación superior, entre otras actividades. Estos elementos propician la motivación por la matemática y su aprendizaje, lo que está en consonancia con González (2022) para quien la motivación regula la dirección, el objeto meta y la intensidad o activación del comportamiento, por lo que se considera por algunos autores que los contenidos que no se haga valer su significado no se convierte en motivación para su aprendizaje.
Se corroboró, además, la correlación existente entre la atención a las diferencias individuales con énfasis en la prevención de las dificultades de los estudiantes en el futuro desempeño relacionado con la solución de las ecuaciones logarítmicas en el grado 11no del IPU ¨Federico Engels¨ de Pinar del Río con el éxito en el aprendizaje y la motivación por el estudio de la asignatura, resultado propuesto por Klingber (1972).
Es por ello que deben tenerse en cuenta la atención a las diferencias individuales con base en el trabajo en el colectivo, y el trabajo preventivo para potenciar el proceso de atención diferenciada y elevar el aprendizaje de los estudiantes hacia niveles cualitativamente superiores. Adicionalmente, lo descrito por Contreras et al. (2021) que plantean entre otros aspectos que diferentes situaciones que pueden aparecer en cualquier ámbito de la vida posibilitan al estudiante argumentar e identificar las ideas fundamentales, establecer juicios, así como analizar la validez de argumentos sobre determinadas proposiciones, logrando un mayor aprendizaje de los estudiantes, tuvo su correspondencia en los resultados obtenidos evidenciado en la necesidad de que la realización de tareas matemáticas exija una distribución adecuada de los recursos de procesamiento mental y memoria, así como el empleo de estrategias ordenadas y jerarquizadas, que implican un encaje progresivo de unos procedimientos en otros.
Es importante considerar además que, para el logro de un mejor aprendizaje, la forma en que se imparten los contenidos juega un papel esencial, ya que se asimilan con mayor rapidez, si se realizan atendiendo a las diferencias individuales tomando como centro el trabajo preventivo y teniendo en cuenta la variedad de formas en que estos se puedan presentar. En esta dirección, es necesario que el profesor promueva la autonomía y gestión del conocimiento por parte del estudiante, considerando como centro del proceso de aprendizaje, entes activos y dinámicos, protagonistas en su proceso de aprendizaje de modo que les permita incentivar el pensamiento crítico a partir del desarrollo de la argumentación y promoción de diferentes estrategias, tal como lo plantean Guzmán et al. (2022)
Sobre esta base se presenta a los estudiantes, el contenido relacionado con las ecuaciones logarítmicas y los elementos del conocimiento que subyacen a la enseñanza de este contenido, como son los tipos de ecuaciones estudiadas en unidades y cursos anteriores (lineales, cuadráticas, fraccionarias, irracionales, trigonométricas), propiedades de los logaritmos, monotonía de la función logarítmica y la definición de logaritmo de un número real mayor que cero.
La estructuración del contenido atendiendo a las diferencias individuales en correspondencia con el desarrollo alcanzado por cada estudiante, constituye una de las normativas de la clase actual que tiene la finalidad de elevar la calidad del proceso educativo con énfasis en lo instructivo, así como la formación de valores y actitudes a partir del trabajo preventivo desarrollado con cada uno de ellos por lo que se sugiere incluir en cada subsistema de clases, tareas que respondan a cada uno de los niveles de desarrollo alcanzado por los estudiantes.
Se considera, entonces, que el proceso de enseñanza-aprendizaje de la Matemática en el preuniversitario propicia el desarrollo en el pensamiento de cada estudiante, sobre la base de la influencia en la esfera afectiva, posibilita que los contenidos aprendidos tengan un significado y un sentido personal, de modo que sirvan de base para los nuevos contenidos que se suceden y que serán necesarios para su accionar en la vida. Tal criterio se corresponde con lo planteado por Munayco y Solís (2021) para quienes la comprensión, invención y resolución de problemas permiten el desarrollo progresivo de las competencias en matemática; existiendo entre ellas una relación de interdependencia.
Al estudiante le es posible, comprender el ejercicio y comenzar su proceso de solución utilizando la orientación dada por el profesor, este propone la preguntas necesarias, creando un clima sociosicológico favorable para que se garantice que el estudiante se involucre en el contexto de formulación y pueda encontrar las estrategias más racionales que le permita dar la respuesta de acuerdo a las condiciones iniciales planteadas en el ejercicio de modo que pueda valorar si es correcto el camino encontrado durante el proceso de solución.
De manera general, se concluye que, en el proceso de enseñanza- aprendizaje de las ecuaciones logarítmicas, el estudiante constituye un ente activo jugando un rol protagónico, donde este revela al profesor el nivel de logros alcanzados en el aprendizaje de estos contenidos, y los límites de su aprendizaje, de modo que le permita al profesor elaborar el perfil de su aprendizaje y actualizar el diagnóstico que se tiene de cada uno de ellos respecto del contenido tratado.
Los resultados obtenidos sugieren que se investiguen, los que se obtengan en los exámenes de ingreso a la educación superior venideros, relacionados con esta temática, en el momento que sean propuestos y compararlos con los históricamente obtenidos tanto en el grado 11no, como con los exámenes de preparación.
La atención diferenciada en el proceso de enseñanza aprendizaje de las ecuaciones logarítmicas en 11no grado con énfasis en el trabajo preventivo constituye un elemento de vital importancia en el aprendizaje y la motivación por el estudio de estos contenidos en este nivel de enseñanza mostrándose a través de la nota media de los estudiantes. El procedimiento propuesto revela la importancia de su aplicación en el logro de niveles cualitativamente superiores en el aprendizaje de la matemática.











 texto en
texto en