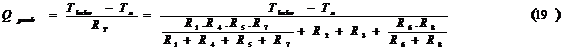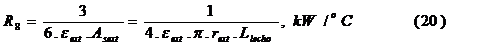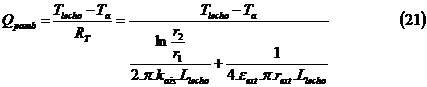Artículo original

Modelo simplificado para evaluar las pérdidas de calor al medioambiente en la zona de gasificación de un reactor de flujo descendente

Simplified model to evaluate heat losses to the environment in the gasification zone of a downdraft reactor

0000-0001-7274-0153René Lesme-Jaen^{1  *}  , 0000-0002-2303-9835Leandro Rodríguez-Ortiz¹  , 0000-0003-4508-1601Odalis Lesme-Jaen² 

¹Universidad de Oriente. Centro de Estudios de Energía y Refrigeración, Santiago de Cuba, Cuba

²Universidad de Oriente. Facultad de Ingeniería Mecánica e Industrial, Santiago de Cuba, Cuba

RESUMEN

La gasificación es uno de los procesos de termo conversión con mayores perspectivas de aplicación para la transformación de la biomasa en un combustible de mayor valor agregado y campo de aplicación. Dentro de las tecnologías que actualmente se utilizan, los gasificadores de flujo descendente son los más difundidos para instalaciones de pequeña capacidad. Durante la evaluación termodinámica de estos gasificadores, una de las pérdidas de energía a tener en cuenta son las pérdidas de calor al medio ambiente y dada variedad de los procesos de transferencia de calor que ocurren dentro del reactor, los métodos de cálculos resultan complejos. En el presente trabajo se desarrolla un modelo simplificado para evaluar estas pérdidas de calor al medio ambiente. El modelo permite desde la etapa de proyecto evaluar las pérdidas en función de las dimensiones del reactor, las propiedades térmicas de los materiales de construcción y la temperatura de trabajo del lecho con un error menor del 1% con respecto al método no simplificado.

Palabras-clave: gasificación; transferencia de calor; reactor de flujo descendente

ABSTRACT

Gasification is one of the thermo conversion processes with the greatest application prospects for the transformation of biomass into a fuel with greater added value and field of application. Within the technologies currently in use, downdraft gasifiers are the most widely used for small capacity installations. During the thermodynamic evaluation of these gasifiers, one of the energy losses to take into account is the heat losses to the environment and given the variety of heat transfer processes that occur within the reactor, the calculation method are complex. In the present work, a simplified model is developed to evaluate these heat losses to the environment. The model allows from the project stage to evaluate the losses based on the dimensions of the reactor, the thermal properties of the construction materials and the working temperature of the bed with an error of less than 1% with respect to the non-simplified method.

Key words: gasification; heat transfer; downdraft reactor

Introducción

La gasificación de la biomasa es su conversión térmica en un gas a través de una serie de reacciones químicas (endotérmicas y exotérmicas) que ocurren a elevadas temperaturas, mediante el uso de aire, oxígeno, vapor de agua o una mezcla de ellos como agentes gasificantes. Este proceso se puede realizarse en diversos tipos de gasificadores (reactores), entre los que se encuentran: reactores de lecho fijo, lecho fluidizado, flujo arrastrado y plasma, la diferencia entre ellos radica en el modo de contacto entre la biomasa y los gases producidos.¹

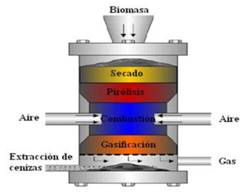
El gasificador de lecho fijo concurrente (downdraft) es el más utilizado para la generación de electricidad a pequeña escala, por su alta eficiencia en la conversión del carbono, produciendo un gas con bajo contenido de alquitrán y ceniza, lo cual minimiza los costos relacionados con su purificación y limpieza del gas.²⁾ En este gasificador la biomasa es suministrada por la parte superior del reactor, el aire por conductos ubicados en las paredes laterales del reactor y el gas se mueve en sentido descendente saliendo por la parte inferior, al igual que las cenizas. El movimiento del gas en sentido descendente permite que el mismo entre en contacto con zonas de mayor temperatura y un mejor craqueo térmico de los alquitranes presentes en el mismo (figura 1).

Fig. 1 Gasificador de lecho fijo concurrente 

Dentro de este reactor durante el proceso de gasificación se pueden distinguir diferentes zonas o regiones: zona de secado, donde ocurre la pérdida de humedad de la biomasa, en esta zona la temperatura está entre(100-200 °C), zona de pirolisis, se produce la liberación de la materia volátil de la biomasa a temperaturas relativamente bajas (400 - 800 °C), zona de oxidación donde ocurre la combustión parcial de la materia volátil y del carbón liberándose el calor, en esta zona las temperaturas puede alcanzar valores por encima de los 1000 °C y la zona de gasificación o reducción del carbón, donde las reacciones secundarias dan lugar a la formación de la mezcla de gases combustibles y cenizas, cuyas temperaturas están alrededor de los 800-1100 ^oC.³

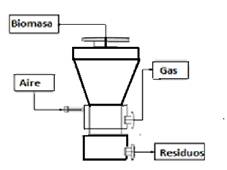
Para la evaluación termodinámica de estos tipos de gasificadores se recurren a los balances de masa (Ec. 1) y energía (Ec.2) ^(4,5,6 en correspondencia con los flujos de relacionados en la (figura 2)

Fig. 2 Entradas y salidas de masa y energía del gasificador 

donde:

M_bio. Flujo de biomasa suministrada al gasificador, kg/h

M_air. Flujo de aire suministrado al gasificador, kg/h

M_gas. Flujo de gas producido, kg/h

M_res. Flujo de residuos, kg/h (Incluye cenizas y alquitrán)

donde:

E_bio. Energía de la biomasa, kW

E_air. Entalpía del aire, kW

E_gas. Energía del gas, kW. Entalpía más energía química del gas

E_res. Energía Residual, kW. Incluye pérdidas de calor con los residuos (Cenizas, carbón y pérdidas de calor al medioambiente)

La determinación de las pérdidas de energía totales se realiza por diferencias entre la energía de la biomasa y el aire y la energía del gas. Se evalúan de forma conjunta de las pérdidas de calor con los residuos y las pérdidas de calor al medioambiente, razón por la cual no es posible establecer la magnitud de cada una de estas pérdidas en el gasificador. En el presente trabajo se desarrolla un método aproximado para evaluar las pérdidas de calor al medioambiente. El método fue aplicado a un reactor downdraft modelo COMBO-80 de fabricación Hindú (figura 3), instalado en el aserrío “El Brujo”, Empresa Gran Piedra Baconao de Santiago de Cuba.

Fig. 3 Gasificador downdraft. Modelo COMBO-80 

Las características constructivas del gasificador y de la biomasa (madera) se reportan en la (tabla 1.)

Tabla 1 Características constructivas gasificador COMBO-80 ⁷  

Este gasificador fue sometido a una evaluación termodinámica cuyos resultados se muestran en la (tabla 2).⁸

Tabla 2 Flujos másicos y energéticos 

Fundamentación teórica

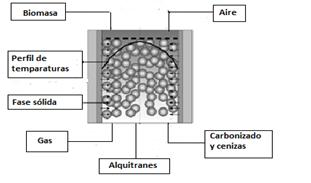
El modelo físico utilizado para evaluar las pérdidas de calor al medioambiente consiste en considerar la zona de gasificación del reactor como un lecho empacado. (figura 4).

Fig. 4 Zona de gasificación 

En el modelo se considera que la temperatura en la zona de gasificación del lecho se mantiene constante, las partículas tienen forma esférica y su diámetro no varía. El proceso de transferencia de calor transcurre de forma estacionaria y unidimensional (Transferencia de calor por conducción y convección en dirección axial es despreciable) y no se tiene en cuenta la transferencia de calor en gases producto de los gases triatómicos ya que la gasificación es un proceso que ocurre con déficit de oxígeno y el por ciento en volumen de estos gases es muy pequeño y prácticamente son consumidos en las reacciones de reformado que ocurren en la zona de gasificación.⁹

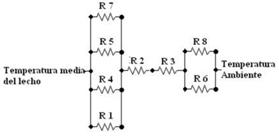
En correspondencia con las consideraciones realizadas en el modelo físico seleccionado se pueden distinguir los siguientes mecanismos de transferencia de calor: transferencia de calor por convección desde el gas a la pared interior del reactor, transferencia de calor por convección del gas a las partículas sólidas que forman el lecho, transferencia de calor por conducción desde las partículas sólidas a la pared interior del lecho, transferencia de calor por radiación del gas a la pared interior del lecho y a las partículas, transferencia de calor por conducción entre las paredes del reactor y transferencia de calor por convección y radiación de la pared exterior del reactor al medioambiente. En la figura 5 se muestra el circuito térmico del proceso combinado de transferencia de calor entre el interior del reactor y el medioambiente.

Fig. 5 Circuito térmico de los procesos de trasferencia de calor en el lecho 

En la figura se pueden identificar 8 resistencias térmicas: resistencia térmica a la conducción entre las partículas y la pared interna del reactor (R₁, Ec. 3), resistencia térmica a la conducción en la capa de material refractario en el interior del reactor (R₂, Ec.4), resistencia térmica a la conducción en la capa de acero en la superficie externa del reactor (R₃, Ec. 5), resistencia térmica a la convección entre el gas y las partículas (R₄, Ec. 6), resistencia térmica a la convección entre el gas y la pared interna del reactor (R₅, Ec. 7), resistencia térmica a la convección entre la pared exterior del reactor y el medio (R₆, Ec. 8), resistencia térmica a la radiación entre las partículas y la pared interior del reactor (R_7, Ec. 9) y resistencia térmica a la radiación entre la pared exterior del reactor y el medio (R₈, Ec. 10).

donde:

h_conwp. Coeficiente de transferencia de calor entre la pared y las partículas, W/m².K

A_p. Área total de partículas en el lecho, m²

donde:

r_1: Radio interior del reactor, m

r₂. Radio interior de la capa de acero, m

k_{ais :} Conductividad térmica del aislante, W/m.K

L_lecho: Altura de la zona de gasificación, m

donde:

r_{3 :} Radio exterior del lecho, m

k_{ace :} Conductividad Térmica del acero, W/m.K

donde:

h_{gp :} Coeficiente de transferencia de calor por convención entre el gas y la partícula, W/m².K

donde:

h_{gw :} Coeficiente de traspaso del calor por convección entre el gas y la pared del reactor, W/m². K (Ec.13)

A_int. Área superficial interior del reactor, m²

donde:

h_ream: Coeficiente de traspaso de calor por convención entre la superficie externa del reactor y el medioambiente, W/m².K (Ec.14)

A_sext: Área de la superficie exterior del reactor, m²

donde:

h_radi. Coeficiente de transferencia de calor por radiación entre las partículas y las paredes internas del reactor, W/m².K (Ec.15)

donde:

h_rade. Coeficiente de transferencia de calor por radiación entre la pared exterior del reactor y el medioambiente, W/m².K (Ec.17)

Los coeficientes de transferencias de calor involucrados en el cálculo de las resistencias térmicas fueron determinados por las siguientes expresiones:

Coeficiente de transferencia de calor entre la pared y las partículas ¹⁰

donde:

K_p. Conductividad térmica de la partícula, W/m.K

Coeficiente de traspaso del calor por convección entre el gas y la partícula ⁽¹¹

donde:

K_g. Conductividad térmica del gas, W/m.K

R_ed. Número de Reynolds.

Pr_rg. Número de Prandtl del gas

El número de Reynolds se determina con la velocidad en la zona libre (V_s=0,55 m/s) y el diámetro de partícula d_p. La velocidad en la zona libre se determina por continuidad conociendo el flujo de gases (m_gas) y el área transversal del reactor.

Coeficiente de traspaso del calor por convección entre el gas y la pared interna del reactor ¹²

Coeficiente de traspaso del calor por convección entre la superficie externa del reactor y el medioambiente ¹³

donde:

R_aL. Número de Rayleigh

Para. Número de Prandtl del aire

Coeficiente de transferencia de calor por radiación entre las partículas y las paredes internas ^14,15

Esta ecuación de forma simplificada se puede expresar de la siguiente forma:

donde:

ϵ_p. Emisividad de las partículas (ϵ_p=0,94)

σ. Constante de Stefan-Boltzman (5,67x10^-3 W/m².K)

Coeficiente de transferencia de calor por radiación entre la pared exterior y el medioambiente ¹⁶

donde:

ϵ_we. Emisividad de la pared exterior (Acero AICI 302, ϵ_we=0,38)

T_we. Temperatura de la pared exterior del reactor. Se asume y se recalcula, K

T_a. Temperatura del aire ambiente, K

Esta ecuación de forma aproximada se puede expresar: ¹⁶

Pérdidas totales al medioambiente

Las pérdidas totales al medioambiente se determinan a partir de la segunda Ley de Newton de enfriamiento teniendo en cuenta las resistencias térmicas involucradas en el proceso combinado de transferencia de calor.

Resultados y discusión

Coeficientes de transferencia de calor

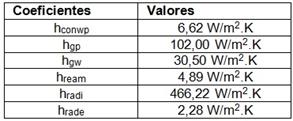
En la tabla 3 se reportan los coeficientes de transferencia de calor por convección en correspondencia con los mecanismos de transferencia de calor considerados en el intercambio de calor entre el interior del lecho y el medioambiente.

Tabla 3 Coeficientes de transferencia de calor por convección 

Como se puede observar los coeficientes de transferencia de calor por convección forzada (h_gp, h_gw) y el coeficiente de transferencia de calor por convección libre (h_ream) están dentro del rango de los coeficientes de transferencia de calor establecidos para gases (25-250) W/m².K y (2-25) W/m².K respectivamente.¹³

Resistencias térmicas al paso del calor

Los resultados de los cálculos de las resistencias térmicas se muestran en la (tabla 4).

Tabla 4 Resistencias térmicas 

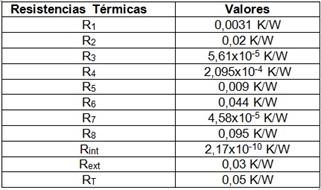
Leyenda: R_int. Resistencia térmica resultante en el interior del lecho

R_ext.: Resistencia térmica resultante en el exterior del reactor

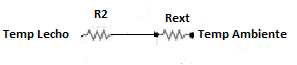
La tabla refleja que resultan insignificantes las resistencias térmicas a la conducción en el acero (R₃), la resistencia térmica a la convección gas-partícula (R₄), la resistencia térmica a la radiación entre las partículas y las paredes internas del reactor (R₇) y la resistencia térmica resultante en el interior del lecho, por lo que el circuito térmico de la figura 5 puede representarse de forma simplificada como se muestra en la figura 6.

Fig. 6 Circuito térmico simplificado 

En la tabla se puede observar que la resistencia resultante en el exterior del reactor es aproximada tres veces mayor que la resistencia térmica a la radiación entre la pared exterior del reactor y el medio por lo que teniendo en cuenta (Ec.10) y la (Ec. 16), esta resistencia puede expresarse como (Ec. 20).

Considerando el circuito térmico simplificado figura 6 y la Ley de Newton de enfriamiento, la ecuación aproximada para evaluar las pérdidas de calor al medioambiente queda expresada como la ecuación 21.

En esta expresión las pérdidas de calor al medioambiente están en función de las dimensiones del reactor, las características térmicas de los materiales de construcción y de la temperatura del lecho, parámetros conocidos desde la etapa del proyecto del gasificador y/o controlables durante el proceso de gasificación.

Pérdidas de calor al medio ambiente

Las pérdidas de calor al medioambiente determinada por la Ley de enfriamiento de Newton para ambos circuitos térmicos, general y simplificado se muestran en la tabla 5.

Tabla 5 Pérdidas de calor al medioambiente 

Se puede observar que las pérdidas al medioambiente en el reactor representan el 8,5 % de la energía de la biomasa. El error que se comete utilizando el método simplificado es de 0,09 %.

Conclusiones

1. Las pérdidas de calor al medioambiente en la zona de gasificación de un reactor downdraft representan el 8,5 % de la energía de la biomasa que entra al gasificador, no es una magnitud despreciable.

2. El modelo simplificado en función de las dimensiones del reactor, la conductividad térmica del aislante y la emisividad de la pared exterior del reactor permite evaluar desde la etapa del proyecto las pérdidas de calor entre la zona de gasificación del reactor y el medioambiente.

3. El modelo simplificado estima con un error del 0,09 % las pérdidas de calor al medioambiente con respecto al método general.

Referencias bibliográficas

1.  MOLINO Antonio, CHIANESE Simeone, MUSMARRA Dino. Biomass gasification technology: The state of the art overview. Journal of Energy Chemistry1.  , 2016, 25(25), pp: 10-25. ISSN: 2095-4956

2.  PRANDO D, SHIVANANDA S Ail, CHIARAMONTI D, BARATIERI M, and DASAPPA S. Characterization of the producer gas from an open top gasifier: Assessment of different tar analysis approaches. Fuel2.  , 2016, 181, pp: 566-572. ISSN: 0016-2361

3.  RUÍZ, J. A, JUÁREZ M. C, MORALES M. P, MUNOZ P, MENDIVIL M. A. Biomass gasification for electricity generation: Review of current technology barriers. Renewable and Sustainable Energy Reviews3.  , 2013, 18, pp: 174-183. ISSN: 1364-0321

4.  MARTÍNEZ González Aldemar, LESME Jaén René, SILVA Lora E.E. Thermodynamic assessment of the integrated gasification-power plant operating in the sawmill industry: An energy and exergy analysis. Renewable Energy4.  , 2020, 147, pp: 1151-1163. ISSN: 0960-1481

5.  APARECIDA Cristina, DIEGO A, LORA Electo, LESME René, M Aldemar, D Juan Experimental study on biomass (eucalyptus spp.) gasification in a two stage downdraft reactor by using mixtures of air, saturated steam and oxygen as gasifying agents. Energy Conversion and Management5.  . 2017,145, pp: 314-323. ISSN: 0196-8904

6.  MARTÍNEZ J Daniel, VIERA Andrade r, SILVA Lora E, LESME Jaén R. Experimental study on biomass gasification in a double air stage downdraft reactor. Biomass and Bioenergy6.  , 2011, 35(8), pp: 3465-3480 ISSN: 0961-9534

7.  OWNER’S MANUAL. ANKUR SCIENTIFIC ENERGY TECHNOLOGIES PVT. LTD. ISO 9001 / ISO 14001 / BS OHSAS 18001 CERTIFIED COMPANY, (2009). Disponible: Disponible: https://www.tradeindia.com/Seller-11664052-Ankur-Scientific-Energy-Technologies-Pvt-Ltd-/ 7.  (Consultada, 26/10/2020)

8.  LESME R, GARCÍA L, OLIVA L, PAJARÍN J, REVILLA D. Biomass Gasification for Power Generation Internal Combustion Engines. Process Efficiency. Revista Tecnología Química8.  , 2016, 36(2), pp: 133-144, ISSN 0041-8420

9.  LISBETH Galindo A, SILVA Lora E, VIERA Andrade R, GIRALDO S Y, LESME Jaén R, MELIAN Cobas V. Biomass gasification in a downdraft gasifier with a two-stage air supply: Effect of operating conditions on gas quality. Biomass and Bioenergy9.  , 2014, 61, pp: 236-244, ISSN: 0961-9534

10.  DIXON, A, CRESSWELL, D. Theorical Prediction of Effective Heat Transfer Parameters in Packed Beds. AIChE Journal10.  , 1979, 25(4), pp. 663-676. ISSN:1547-5905

11.  ISMAIL, K.A, STUGINSKY, R., 1999. “A parametric study on possible fixed bed models for pcm and sensible heat storage”. Applied Thermal Engineering11.  , 1999, 19, pp: 757-788, ISSN: 1359-4311

12.  GALLOWAY T.R, SAGE B.H. A model of the mechanism of transport in packed distended and fluidized beds. Chemical Engineering Science12.  . 1970, 25, pp: 495-505, ISSN: 0009-2509

13.  INCROPERA Fran P, DE WITT David P. Fundamentos de transferencia de calor13.  . 4ta. Edición, México. 1999. ISBN 970-17-0170-4

14.  ISMAIL, K.A, STUGINSKY, R. “A parametric study on possible fixed bed models for pcm and sensible heat storage”. Applied Thermal Engineering14.  , 1999, 19, pp: 757-788 ISSN: 1359-4311

15.  VEDAT S. A., SHU H.K, AHMET S. Introduction to heat transfer15.  . Prentice Hall. Unite State of America, 1999. ISBN: 0-13-391061-X

16.  MILLS A.F. Transferencia de calor16.  . McGraw-Hill/Irwin.España.1999. ISBN 8480861940

Recibido: 15 de Diciembre de 2021; Aprobado: 08 de Abril de 2022

Los autores declaran que no hay conflictos de intereses

René Lesme Jaén: participó en la evaluación termodinámica del gasificador, procesamiento de datos experimentales, así como, en el desarrollo del modelo, elaboración, revisión y aprobación final del artículo.

Leandro Rodríguez Ortiz: participó en la evaluación termodinâmica del gasificador en el desarrollo del modelo, elaboración, revisión y aprobación final del artículo.

Odalis Lesme Jaén: participó en en el desarrollo del modelo, elaboración, revisión y aprobación final del artículo.