INTRODUCCIÓN
Se han realizado diferentes estudios relacionados con la determinación de los rendimientos de madera aserrada, teniendo en consideración las características de la madera en bolo, la utilización de la estadística y la programación matemática, pero presentan la limitante de que no tienen en consideración las variables dendrométricas y la calidad de los árboles en pie, sin las cuales la planificación de las actividades relacionadas con el suministro de madera no presenta la exactitud deseada (Sharna y Zhang, 2004; Zhang et al., 2005, Liu et al., 2007 y Estremera y Rodríguez, 2021).
Sin embargo, en trabajos desarrollados en Canadá, Estados Unidos, Alemania, Suecia, si toman en consideración las características dendrométricas de los árboles en pie para predecir los rendimientos de madera aserrada (Zhang et al., 2006 y Liu et al., 2007). Así se establece que es fundamental en los procesos de aserrado de la madera tener en consideración la relación existente entre los rendimientos de madera aserrada y las características dendrométricas de los árboles.
El establecimiento de la relación entre las características de los árboles y el valor del producto pueden ser utilizados en la industria de transformación mecánica de la madera para estimar el potencial de los árboles individuales y del rodal antes de ser talados. Esta relación puede ser útil para el desarrollo estratégico del manejo forestal sostenible.
El objetivo del presente trabajo fue emplear modelos matemáticos para la predicción de los rendimientos de la madera aserrada a partir de parámetros dendrométricos de los árboles en pie que permitan una adecuada definición de su potencial en el aserradero.
MATERIALES Y MÉTODOS
El trabajo se desarrolla en el aserradero Combate de la Tenería de Guane, perteneciente a la Empresa Agroforestal Macurije, ubicada en la región más occidental de la provincia de Pinar del Río, abarcando partes de los territorios de los municipios Guane y Mantua.
Determinación del tamaño de la muestra e intensidad del muestreo
Los datos fueron tomados de una población de 954 árboles perteneciente a los rodales 21 y 19 del lote 22 de la Unidad Silvícola Guane, de los cuales mediante un muestreo aleatorio se tomó una muestra piloto de 58 árboles para determinar el número de unidades representativas para el estudio, teniendo como variable de interés el diámetro a 1.30 m de altura del árbol, para determinar el número de unidades representativas para el estudio, a partir de la siguiente ecuación para población infinita (Ortiz et al., 2016 y Borges et al., 2019). Ecuación 1:
Donde: n- tamaño de la muestra; t 2 á- valor tabular de t (a = 0,05); con (n-1) grados de libertad; S2 Varianza estimada; E Error admisible (10 %); N- número total de árboles medidos.
De la cual resultó una muestra de 106 árboles que se marcaron en pie y después de ser talados se les midieron los diámetros a 1.30 m, diámetros de los extremos de las trozas y sus longitudes, se hace necesario este procedimiento de marcaje por la posterior identificación y medición de las variables en el aserrío como son la conicidad y volumen de las trozas y volumen de madera aserrada.
Modelación matemática de la influencia de los parámetros dendrométricos de los árboles en pie sobre los rendimientos de madera aserrada
Para obtener el rendimiento en porcentaje se empleó la siguiente relación a partir de los trabajos realizados por Barth et al. (2016); Cevallos et al. (2017) y Leyva et al. (2017). Ecuación 2:
Donde: Rv - Rendimiento volumétrico total, %; Vma- Volumen de madera aserrada, m3; Vt- Volumen de madera en trozas, m3.
El volumen de madera aserrada total en cada troza en los aserraderos se determina sobre la base de las mediciones lineales obtenidas de la madera aserrada de acuerdo con las expresiones que se exponen a continuación (Orozco et al., 2016 y Leyva et al. 2020). Ecuación 3:
Donde: Vma- Volumen de madera aserrada de una troza, m3; a, g, l ancho, grueso y longitud de la pieza i obtenida de una troza o grupo de troza, m; n- Número de piezas aserradas de una troza
El cómputo del volumen en bruto de cada troza se efectúa a través de la fórmula de Smalian en correspondencia con los trabajos desarrollados por Alzamora et al. (2019) y Casagrande et al. (2019) Ecuación 4:
Donde: Vmb- volumen de la en bolo (m3); g1, área basal en el extremo fino (m2); g2, área basal en el extremo grueso (m2); L, longitud de la troza (m).
Para la predicción de la estimación del rendimiento de la madera aserrada se empleó la regresión lineal simple, múltiple y por pasos, teniendo en consideración los modelos que se muestran a continuación, Ecuación 5, 6, 7 y 8:
Para la determinación de la conicidad de los árboles en pie se tomó como referencia trabajos realizados por Kozakiewicz et al. (2018) y Álvarez et al. (2020), que tienen en consideración el valor inferior de las dos primeras trozas, empleando para ello la siguiente expresión matemática Ecuación 9:
Dónde: Con-conicidad, cm /m; D1 -Diámetro menor de la troza, (cm); D2 - Diámetro mayor de la troza, (cm); L - Longitud de la troza, (m)
Como variables independientes o predictoras se utilizaron diámetros a la altura de 1.30 m (d1.30), la altura del fuste (comercial) y la conicidad y se utilizó como variable de respuesta o dependiente el rendimiento de la madera aserrada.
En la determinación de la calidad de los modelos planteados se tuvieron en consideración los siguientes aspectos:
Supuestos teóricos: normalidad, homocedasticidad e independencia serial de los residuos mediante la prueba de Durbin Watson. La presencia de multicolinealidad entre las variables predictoras, es evaluada mediante el factor de inflación de la varianza (VIF) (Maddala, 1996 y Najera et al., 2012), asumiéndose para aquellas ecuaciones que presentaron un VIF superior a 10 para algunas de sus variables independientes
Bondad de ajuste: coeficiente de determinación ajustado (R^2 adj), el error estándar de la estimación (Sx) y la significación estadística de los coeficientes de regresión ajustados. Aquellos modelos que presentaron al menos un parámetro no significativo distinto de cero fueron eliminados.
Validación de los modelos de regresión
Se plantea que el proceso más importante después de que se ha obtenido un modelo es el de validación. Su principal objetivo es asegurar que los resultados sean generalizados a toda la población y no específicos de la muestra utilizada en la estimación (Hair et al., 1999).
Los datos empleados para la validación son diferentes de los utilizados para el ajuste de los modelos; coincidiendo con los planteamientos de Alder (1980). Se emplearon el sesgo y el error cuadrado medio como estadísticos de predicción Ecuación 10:
Donde: Ç- sesgo; Yi- valor observado; Y i - valor predicho; N- número total de datos empleados Ecuación 11:
Donde: Donde: EMC-error cuadrado medio; Yi- valor observado; - valor predicho; N- número total de datos empleados; P-número total de parámetros a estimar
Modelo de evaluación utilizando el análisis de elasticidad
Los rendimientos en valores de la madera aserrada a partir de árboles individuales se cuantificarán en función del diámetro a 1. 30 m, el diámetro de la rabiza del árbol, la altura total del árbol, la altura de la primera rama del árbol, la altura de la copa del árbol y la conicidad del fuste; por lo que se tiene la siguiente expresión; coincidiendo con Zhang et al. (2005). Ecuación 12:
Donde: Rf- Representa los valores del Con- Conicidad del fuste, (cm/m).
Las elasticidades de las salidas se determinaron de las siguientes maneras Ecuación 13 y 14:
Para d1.30 m
Para la conicidad
Determinación de la variación de aserrado a partir de la implementación del control estadístico del proceso de aserrado
Para la realización del análisis pertinente, en el aserradero Combate de la Tenería, se han tomado 100 piezas aserradas de Pinus caribaea coincidiendo con la metodología propuesta por Leyva et al. (2017) y Álvarez et al. (2020).
A cada pieza de madera aserrada, se le tomaron seis mediciones, tres en cada canto, en forma equidistante a lo largo de las mismas, teniendo el cuidado de establecer una secuencia permanente de las mediciones respecto a la dirección de salida de las piezas de la sierra, con el objetivo de identificar eventuales problemas en los equipos. Las mediciones se realizan con un pie de rey hasta la precisión de la décima de milímetro, en áreas de madera sana, evitando nudos, pudriciones y otros defectos.
Debido a la complejidad y volumen de los cálculos, sobre todo en el cómputo de las variaciones de grosor en el aserrío cuando se dispone de una muestra grande, fue necesario encontrar una herramienta ágil y factible para el procesamiento de los datos, por lo que se utiliza el programa CONTROL (Álvarez et al. 2020)
Para ello, se utilizó el software Control versión 5.1 que permite determinar las dimensiones óptimas de aserrío; así como la determinación de la variación en grosor, el cual se basa en la formulación planteada por Brown (1986) y Álvarez et al. (2020), para el cálculo de la dimensión óptima del surtido y de otros parámetros que a continuación se describen Ecuación 15:
Cálculo de la dimensión óptima (Do)
Dónde: Do -Dimensión óptima de corte de madera verde, mm; DF- Dimensión final, mm; TC- Tolerancia por cepillado en ambos lados del surtido, mm; %C- Tolerancia por contracción de la madera, %; Z- factor de dimensión mínima aceptable (adimensional); St- Variación total de aserrado, mm Ecuación 16, 17 y 18:
Sd- desviación estándar del proceso de aserrado dentro de las piezas (mm);
Se- desviación estándar del proceso de aserrado entre piezas, mm.
Donde: -representa la varianza de las medias de los grosores de cada pieza muestreada; n-número de mediciones por pieza.
Por otra parte, se debe tener en consideración la variable dimensión crítica (Dc), que está relacionada con la dimensión de la madera verde, si se pudieran producir piezas sin variación de aserrado. La expresión matemática que posibilita determinar esta dimensión es la siguiente Ecuación 19:
Los datos de las muestras analizadas son procesados a partir del programa CONTROL, considerando los siguientes aspectos específicos:
DF = 25 mm;
TC = 0;
C- Contracción tangencial de la madera de Pinus caribaea de 4,30 % según Ibáñez (1975); Z- 5 % de acuerdo con Zavala (1991), Nájera (2011) y Álvarez et al. (2020).
RESULTADOS Y DISCUSIÓN
Determinación de los rendimientos de madera aserrada
En la Figura 1, se aprecia que los rendimientos de madera aserrada van decreciendo desde la base hasta la rabiza; lo cual es consecuencia directa del aumento de la conicidad por el decrecimiento de los diámetros con la altura; esto coincide con Najera et al. (2012).
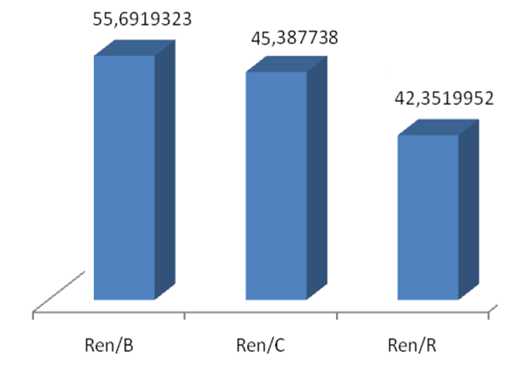
Fig. 1. - Frecuencia del rendimiento en diferentes posiciones del fuste del árbol. Ren/B-rendimiento en la base (%); Ren/C- rendimiento en el centro (%); Rend/R-rendimiento en la parte superior (8 %).
Los resultados antes expuestos demuestran que el diámetro es una variable dendrométrica que presenta una relación directa con los rendimientos de madera aserrada, lo cual fue similar a lo reportado por (Ortiz et al., 2016, Álvarez et al. (2020) y Leyva et al. (2020).
En la medida que el diámetro aumenta, también se incrementa el rendimiento de las trozas en el aserrado. Lo que implica en el procesamiento de madera de pequeñas dimensiones, bajos niveles de rendimiento y menos ganancia para el aserradero.
Modelos para estimar el rendimiento de madera aserrada a partir de las variables dendrométricas
Utilizando las variables independientes de mayor relación con la variable dependiente y de respuesta se obtuvieron ecuaciones de estimación del rendimiento de madera aserrada, los modelos comparados se observan en la Tabla 1, con sus respectivos coeficientes de determinación (R2) y error estándar de estimación (S).
Tabla 1. - Modelos para determinar el rendimiento de la madera en árboles en pie
| Modelos de regresión | R2 | S |
| Ln (rend) = 1,013 + 0,0519 * ln d1.30 (20) | 0,657 | 0,032 |
| Ln (rend) = 1,084 + 0,464 * ln d1,30 - 0,1201 ln Con (21) | 0,671 | 0,031 |
| Ln (rend)= ln 7,27119601 + (1,02303964 * ln (d1,30)) (22) | 0,654 | 0,11 |
| Ln (rend) = ln 0,16089255 + (ln (1,2660825) * d1,30) (23) | 0,657 | 0,11 |
Las cuatro ecuaciones construidas para determinar el rendimiento de la madera aserrada tienen aceptables coeficientes de correlación, determinación y bajos errores estándar de estimación. Sin embargo, el mejor comportamiento lo posee el modelo (20):
Ln (rend) = 1,084 + 0,464 * ln d1,30 0,1201 ln que tiene mejor ajuste (las variables independientes explican el 67 % y el menor valor del error estándar de estimación.
El presente modelo cumple, además, con los supuestos de independencia de Durbin-Watson con un valor de 2,038, la homogeneidad de la varianza y el supuesto de multicolinealidad con una tolerancia de 0,308.
En la Tabla 2, se aprecia la capacidad de predicción del modelo que aporta los mejores resultados, apreciando los bajos valores del error cuadrado medio, sesgo y desviación estándar de los residuos. Estos resultados expuestos se corresponden con los obtenidos por Sánchez et al. (2003).
Modelo de evaluación utilizando el análisis de elasticidad
Las relaciones derivadas de los modelos de regresión se pueden utilizar para caracterizar algunas propiedades, entre las que se destacan las elasticidades y la interacción entre las variables dependientes e independientes (Liu et al., 2007).
Las elasticidades de las salidas en el modelo Ln (rend) = 1,084 + 0,464 * ln d1,30 0,1201 ln con en el caso de madera aserrada se ilustran de la siguiente manera Ecuación 20 y 21:
Para d1.30 m
Para la conicidad
La contribución de las variables predictoras sobre el rendimiento de la madera aserrada es de:
0,464 d1,30 m
- 0,120 para la conicidad
Lo cual indica que el d1,30 m es el factor de mayor significación e influencia sobre el volumen de madera aserrada producida de manera positiva. Por otra parte, la Conicidad presenta un efecto negativo, lo que posibilita establecer que los rendimientos de madera aserrada decrecen con un incremento de la conicidad (Tong y Zhang, 2006).
El valor relativo de la madera aserrada presenta un incremento en función del d1,30 m, que se cuantifica a partir de la siguiente expresión matemática Ecuación 22:
Lo cual establece que el incremento de un 1 % del d1,30 puede ocasionar un incremento aproximado del 0,464 % del rendimiento en valor de la madera aserrada, lo cual denota una contribución positiva del d1,30 m sobre la magnitud del valor de la madera aserrada.
Es significativo definir que la conicidad presenta un efecto inverso tal y como se expone en la siguiente expresión matemática Ecuación 23:
Con lo cual se establece que el incremento en 1 % de la conicidad provoca un efecto negativo o reducción de los rendimientos en valores de la madera aserrada en el -0,120 %; coincidiendo con Zhang et al. (2006).
Control estadístico del proceso de corte en el aserradero Combate de la Tenería de Guane
En el aserradero Combate de la Tenería, perteneciente a la EAF Macurije, Pinar del Río, existe un sobredimensionamiento generalizado de la madera aserrada, lo cual se aprecia en la Tabla 3. Estos resultados coinciden con los obtenidos por Álvarez et al. (2020) y Leyva et al. (2020).
Tabla 3. - Resultados relacionados con el análisis de la variación de aserrado en el aserradero Combate de la Tenería
| Parámetros | Piezas de 25 mm de grosor | |
| Pieza de 3 m de longitud | Pieza de 4 m de longitud | |
| Dimensión óptima (Do), mm | 26,40 | 27,50 |
| Dimensión final (Df), mm | 25,00 | 25,00 |
| Dimensión óptima (Do), mm. | 26,30 | 27,54 |
| Dimensión crítica (Dc), mm. | 25,48 | 25,48 |
| Variación dentro de las piezas (Sw), mm | 0,00371 | 0,0726 |
| Variación entre piezas (Sb), mm | 0,0210 | 0,07 |
| Variación total del proceso (St), mm. | 0,0427 | 0,11 |
De acuerdo con los valores medios de grosor para las piezas representadas en la Tabla 3, se muestran valores para la especie, por encima de lo establecido como dimensión final (25 mm), con variaciones mayores a 1,5 mm, representando una considerable pérdida de madera aserrada, lo cual implica la necesidad de desarrollar en el aserrío el proceso de control estadístico del proceso; coincidiendo con Barrera et al. (2016).
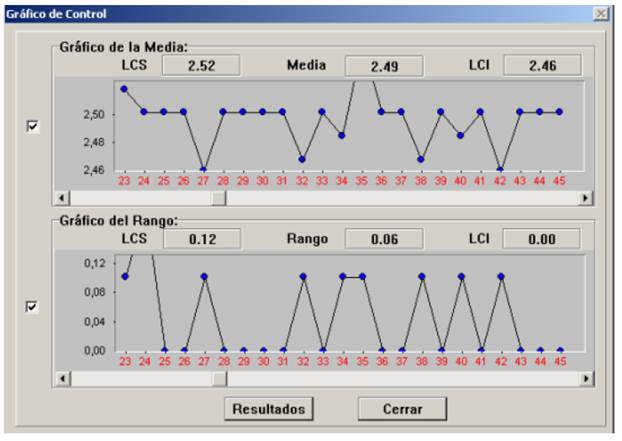
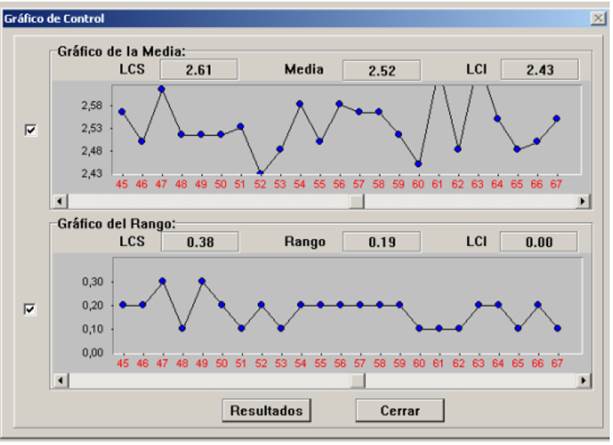
El empleo del programa Control para la determinación de las dimensiones óptimas de madera aserrada, así como la construcción de gráficos de control (Figura 2 y Figura 3). Esto constituye una herramienta adecuada para tomar decisiones dirigidas a aumentar los rendimientos y calidad de la madera aserrada; exponiendo que la automatización constituye una excelente herramienta para el manejo de datos y toma de decisiones en los aserraderos.
CONCLUSIONES
Las contribuciones de las variables predictoras en los rendimientos de madera aserrada indican que el diámetro a 1,30 m es el factor de mayor significación.
En función del análisis de elasticidad, se puede definir el diámetro a 1,30 m la variable predictora de mayor influencia positiva sobre el incremento de los rendimientos de madera aserrada.
El empleo del programa Control para la determinación de las dimensiones óptimas de madera aserradas, así como la construcción de gráficos de control, constituye una herramienta adecuada para tomar decisiones dirigidas a aumentar los rendimientos y calidad de la madera aserrada.











 texto en
texto en