Introducción
En la actualidad, el desarrollo de la vida humana depende del aporte de una gran cantidad de energía obtenida principalmente de la oxidación de combustibles fósiles, que son recursos no renovables de disponibilidad limitada, cuyo empleo ha aumentado la contaminación del medio ambiente provocando severos cambios climáticos [1]. La energía solares un recurso limpio, que tiene el potencial de satisfacer las necesidades de la población mundial proporcionando anualmente una cantidad de energía de aproximadamente 108 veces la utilizada por todos los seres humanos en el mismo período [2].
Cuando la radiación solar interactúa con un semiconductor se obtiene electricidad debido a que estos materiales permiten la fotoemisión de electrones. Asimismo, la radiación solar puede aprovecharse en procesos térmicos al concentrar los rayos incidentes en el foco de una superficie especular llamada concentrador. Puede entonces ubicarse en este foco un receptor que absorbe la energía solar concentrada y la transfiere como calor al fluido que circula en su interior para finalmente ser utilizada en procesos industriales que requieren energía térmica o en la producción de energía eléctrica [3].
En las tecnologías que tratan la concentración de la radiación solar, los espejos que constituyen el concentrador son componentes claves en el proceso de conversión de energía, ya que si la radiación solar no es reflejada en la dirección del receptor existirá una pérdida en la eficiencia del sistema. En consecuencia, es importante contar con espejos de alta reflectancia, parámetro que determina la cantidad de radiación incidente que es reflejada por el espejo. Es necesario que los errores de curvatura (errores de pendiente) del concentrador sean pequeños y como el concentrador suele construirse con facetas espejadas, que el error de alineamiento de las mismas sea bajo [4].
Los sistemas de energía solar térmica de concentración más estudiados pueden ser agrupados según su modo de enfocar los rayos solares en: i) sistemas de enfoque longitudinal como los cilindros parabólicoy de Fresnel que siguen el movimiento aparente del Sol a lo largo de un eje; ii) sistemas de enfoque radial, como los de torre central y de disco parabólico, que siguen al sol a lo largo de dos ejes [5].
Solamente el sistema de disco parabólico logra mantener el eje óptico alineado con el Sol en todo el seguimiento diario, como consecuencia, logra una mayor eficiencia en la recolección del recurso solar en comparación con los otros sistemas [6]. Los rayos incidentes en el disco concentrador se reflejan en una misma región focal, generando un área de alta exergía con temperaturas superiores a 800 °C [7]. Estas temperaturas elevadas permiten una alta eficiencia en la conversión de energía termo-mecánica y, en consecuencia, alta eficiencia de conversión de energía solar a eléctrica, cuando se combina con una máquina térmica (motor Stirling, turbina Rankine, turbina Brayton, etc) [8, 9].
Para determinar la cantidad de energía térmica disponible en el área del receptor, es indispensable conocer la calidad óptica del concentrador. Por esto, es necesaria su caracterización a través de mediciones precisas, económicas y rápidas. Se han propuesto y aplicado una variedad de métodos ópticos, tales como los de barrido de pendiente con haz láser, análisis de patrones trazados sobre la superficie reflectiva, análisis de patrones reflejados por el concentrador, etc. Es importante destacar que muchos de estos métodos se han desarrollado para evaluar concentradores con facetas espejadas curvadas [10].
Existen también técnicas utilizadas en otros campos, además de la óptica, que se han adaptado a la evaluación de los concentradores solares con resultados satisfactorios, entre estas últimas el uso de calorímetros.
Diferentes autores proponen que utilizando calorímetros en los que existe una variación constante de masa de un fluido que se calienta por acción de los rayos solares, y midiendo el incremento de la temperatura que ocurre en fluido al atravesar el calorímetro, es posible medir la potencia térmica entregada por el concentrador [11, 12, 13]. Estos dispositivos requieren de caudalímetro de precisión, bombas de agua, refrigeradores, tanques, tuberías, etc.
En el Laboratorio de Óptica, Calibraciones y Ensayo (LOCE) como parte de un proyecto interinstitucional, se construyó un disco parabólico prototipo, con facetas espejadas triangulares planas, para producir electricidad utilizando como receptor un motor Stirling [14].
De acuerdo a la bibliografía, no hay una oferta suficiente de métodos simples y económicos que permitan la rápida evaluación de espejos concentradores construidos con facetas planas. Para medir la calidad óptica de este concentrador se propone un método sencillo que no requiere de instrumental complejo para su implementación, denominado calorímetro de masa constante.
En este trabajo, se realiza una validación de los resultados obtenidos utilizando dos métodos diferentes, para tal fin se comparan los resultados del ensayo realizado con el calorímetro de masa constante con aquellos obtenidos mediante un método óptico ampliamente difundido para analizar la eficiencia del concentrador de disco parabólico prototipo, conocido como ensayo del barrido óptico de Hartmann (SHOT, Scanning Hartmann Optical Test), que emplea un láser como fuente de luz puntual que simula al Sol [15]. Debido a que el concentrador fue construido con facetas planas, es necesaria una simulación adicional por método Monte Carlo utilizando los datos experimentales obtenidos con el ensayo SHOT.
Materiales y métodos
Diseño del prototipo de disco parabólico
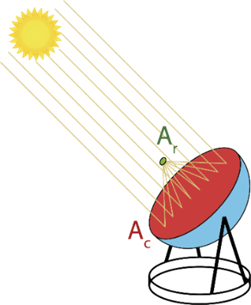
El dispositivo consta de dos componentes principales: el concentrador, compuesto por una superficie reflectante que se aproxima a un paraboloide de revolución; y el receptor, ubicado en el área focal del espejo concentrador, figura 1. Como el eje óptico del disco prototipo se encuentra alineado con el sol, los rayos incidentes en el concentrador se reflejan en una misma región focal, generando un área de alta exergía debido a la conjunción de los rayos reflejados.
La superficie reflectante concentra la luz solar incidente de un área plana (Ac), definida como plano de apertura, en un área de concentración focal (Ar). Se define el parámetro Relación de Concentración (RCR) como:vea ecuación (1):
En la zona focal, el receptor absorbe la radiación solar reflejada por el concentrador y la transforma en energía térmica.
La eficiencia óptica del sistema, ηop, se define como la relación entre la energía solar entregada al receptor, Pr, y la energía solar que llega al concentrador, Pc, [5]. Vea ecuación (2):
El concentrador del prototipo que se muestra en la figura 2, tiene un diámetro de 1,50 m y un área Ac de 1,77 m².
A diferencia de los concentradores convencionales, este prototipo fue confeccionado con facetas espejadas triangulares planas equilateras de 0,078 m de lado, ensambladas para reflejar los rayos solares incidentes en la zona focal. Es de destacar que en el prototipo que se estudia, toda el área expuesta a la radiación solar está cubierta con espejos, en contraposición a otros concentradores construidos con facetas planas espejadas de otras formas geométricas, que dejan espacios sin espejo por discordancia de forma [16].
Como el concentrador se encuentra construido con facetas de superficies planas no existe una curva ideal que los represente, por lo que no puede hablarse de un error de pendiente. En cambio, el error de alineamiento de las facetas es el principal error que afecta a la eficiencia del sistema.
Para medir la eficiencia óptica, ηop, se utiliza un calorímetro de masa constante ubicado como receptor en el área focal del concentrador. El calorímetro contiene agua que absorbe la energía solar que llega desde el concentrador en forma de energía térmica.
Calorímetro de masa constante
El calorímetro consiste de un cilindro metálico de pared gruesa de acero con varios orificios para: la entrada de agua, la colocación de termopares, una válvula de seguridad y un manómetro con el cual medir la presión interior.
En su cara expuesta al concentrador solar, el calorímetro tiene una tapa compuesta por un anillo metálico grueso con un diámetro externo de 0,18 m y un diámetro interno de 0,09 m. El orificio central de ese anillo es cerrado con una tapa de vidrio de 0,02 m de espesor, que posibilita la entrada de rayos solares.
La superficie exterior del calorímetro tiene como aislante una cubierta de espuma de polietileno de 0,01 m de espesor. Esta cobertura polimérica está revestida externamente por una lámina de aluminio reflectante que minimiza las pérdidas térmicas debidas a la emisión radiativa, figura 3.
Principalmente, el calorímetro pierde energía térmica debido a los procesos convectivos y radiativos, que dependen de la temperatura del calorímetro, la calidad del aislamiento y las condiciones climáticas.
Ensayo de barrido óptico de Hartmann SHOT
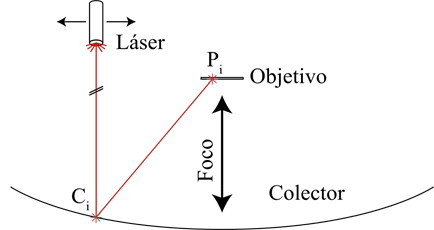
Debido a las particularidades del concentrador prototipo (facetas planas) se realiza el ensayo SHOT modificado para determinar ηop. La modificación del ensayo SHOT consiste en ubicar un láser autonivelante a 6 metros de altura, como un objeto luminoso posicionado en el infinito óptico. El concentrador se coloca con su plano de apertura perpendicular al haz incidente. Mediante una plataforma mecánica es posible desplazar el láser en coordenadas (x, y) logrando que incida en el centro de cada una de las facetas triangulares seleccionadas en el concentrador para realizar la medición.Cuando el haz láser es dirigido al centro de un espejo triangular, resulta reflejado en un objetivo, iluminando un punto sobre el mismo. El objetivo, que está ubicado en el foco del concentrador, cuenta con una cuadrícula graduada que permite medir la posición de dicho impacto en coordenadas (x, y), figura 4 y figura 5.
Se ensayan 309 facetas espejadas, escogidas de forma aleatoria, conformando una porción representativa del concentrador. Para cada espejo analizado se obtiene un punto Ci de coordenadas (x,y,z) en el centro del espejo y un punto de impacto Pi de coordenadas (x,y,z) en el objetivo.
Utilizando el conjunto de datos Pi puede obtenerse el factor de intercepción (γ) sobre un área determinada mediante la siguiente expresión (3):
Al disminuir el tamaño del área receptora también lo hace γ, puesto que menos rayos impactarán en dicha área. Sin embargo el flujo radiante medio aumenta puesto que la porción central receptora cuenta con una mayor intensidad radiativa que la periferia. Un mayor flujo radiante medio implica tener mayor exergía y menores zonas expuestas al ambiente, disminuyendo las pérdidas térmicas del receptor. Es por esto que debe elegirse un área receptora con un valor de compromiso para interceptar la mayor cantidad de energía sin disminuir en demasía el flujo radiante medio.
Como se pretende realizar una validación del método del calorímetro de masa constante a través de la comparación de los resultados obtenidos por ese método y los obtenidos por el ensayo SHOT, el área de impacto elegida coincidirá con la de un círculo de 0,09m de diámetro, idéntico a la ventana de entrada del calorímetro.
La eficiencia óptica se relaciona con γ a través de la ecuación(4), [17]:
Donde ρ es la reflectancia de los espejos, siendo ρ = 0,95 el valor considerado para espejos de la calidad empleada [18].
Debido a que el láser solo impacta en una pequeña área central de cada faceta es necesario realizar un análisis más riguroso en la determinación de ηop. Para esto, se realiza una simulación computacional que toma en cuenta el área total de la faceta.
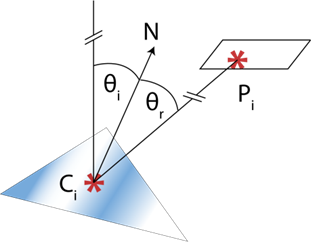
Considerando cada faceta triangular como un espejo plano y siendo que el ángulo de incidencia es igual al ángulo de reflexión, como se observa en la figura 5, puede obtenerse un vector normal a la superficie de cada espejo medido utilizando el conjunto de puntos experimentales.
Las simulaciones Monte Carlo suelen utilizarse para describir procesos de flujos, en particular flujos radiativos. Es por esto que es una herramienta habitual en el análisis de potencias lumínicas en sistemas ópticos.
Con el conjunto de vectores normales se construye un modelo CAD de los espejos para utilizarlo en el programa Tonatiuh Ray Tracer [19], y realizar una simulación por método Monte Carlo (figura 6), obteniéndose un mapa de intensidad lumínica de la zona focal. La simulación utiliza una distribución de Buie para los rayos solares, considerada válida para dicho propósito [20]. La reflectividad de los espejos es ρ = 0,95 y los errores pendiente son nulos.
Resultados y discusión
Método del calorímetro de masa constante
Midiendo la variación de la temperatura del agua del calorímetro en función del tiempo se obtiene la potencia térmica útil Pt según ecuación (5):
Donde dT es una variación infinitesimal de la temperatura del agua del calorímetro durante una variación infinitesimal de tiempo dt. Teniendo en cuenta la masa de acero, agua y vidrio, así como los calores específicos de cada material, la capacidad calorífica del calorímetro resulta C = 15 700 ± 100 J/°C y se considera constante en el rango de temperatura medido.
La potencia térmica del calorímetro puede disminuir a causa de dos fenómenos: 1) parte de la radiación solar no ingresa al calorímetro debido a su reflexión en la ventana de vidrio que cubre la parte frontal, (Ppr); 2) existen pérdidas de potencia térmica, Ppt, debido a la emisión radiativa, la convección y la transferencia térmica de contacto, que dependen de la temperatura del calorímetro, la calidad del aislamiento y las condiciones climáticas.
Las pérdidas de potencia térmicas de contacto asociadas a la unión de las asas metálicas del calorímetro a la estructura del disco parabólico no se tienen en cuenta en este trabajo por considerarse pequeñas.
Tomando en cuenta las pérdidas de potencia térmicas (Ppt), reflectivas (Ppr) y considerando la ecuación (2), a partir del valor de potencia Pt obtenido de la ecuación (5), es posible determinar el valor de la eficiencia óptica: vea ecuación (6):
donde Is es la intensidad de la radiación solar que llega al concentrador.
En un experimento realizado previamente y descrito en [21], el calorímetro se calienta hasta 85°C, se desconecta de la fuente de calor, a continuación se mide la variación temporal de su temperatura interna durante el enfriamiento y se calcula la pérdidade potencia térmica Ppt = 62,5 ± 0,5 W.
Para conocer el valor de la pérdida de potencia reflectante, Ppr, el ángulo máximo de incidencia del plato parabólico se fija en 46 °. Luego, recurriendo a las fórmulas de Fresnel y Snell se determina la cantidad de radiación solar reflejada por la primera y segunda superficie de la cubierta de vidrio, que expresadas en porcentaje de la radiación incidente (Is), resultan 4,6% y 0,6%, respectivamente.
Evaluación de la eficiencia óptica del concentrador
Para determinar la eficiencia óptica del sistema; el calorímetro se coloca a 0,87 m del vértice del concentrador, de modo que la ventana del calorímetro coincida con el área receptora de la radiación solar reflejada por el concentrador, como se muestra en la figura 7.
Las experiencias se realizaron en días despejados con baja humedad relativa para evitar la dispersión de los rayos solares. En todas las experiencias se establece el valor máximo de la temperatura del agua en 85° C.
Al inicio de cada ensayo, se deja reposar el agua del calorímetro durante unos minutos para lograr el equilibrio térmico. Luego, el concentrador se orienta hacia el Sol y se sigue su posición de forma continua para alcanzar la máxima concentración de rayos. Se realizaron trece experimentos con el calorímetro como receptor durante marzo, a principio de otoño en la ciudad de La Plata. Los valores de intensidad de la radiación solar global fueron proporcionados por una estación meteorológica modelo Davis Vintage Pro 2 ubicada en el sitio donde se realiza el experimento. Los valores de Is con su corrección por ángulo de incidencia se utilizaron en la ecuación (6), para calcular la eficiencia óptica del concentrador.
La eficiencia óptica promedio ηop para el concentrador resulta 0,71 ± 0,02, con este valor, utilizando modelos meteorológicos como el año solar típico podría calcularse la energía térmica anual que puede recolectar el concentrador en cualquier sitio.
Medidas de la eficiencia óptica por el método SHOT modificado
Utilizando como una primera aproximación las ecuaciones (3) y (4), el conjunto de puntos Pi dentro del el círculo central de 0,09 m de diámetro, se obtuvo un factor de intercepción γ = 0,74 ± 0,02 y un valor de eficiencia óptica ηop= 0,70 ± 0,02 (figura 8). Se debe tener en consideración que el haz láser solo impacta el centro de cada faceta, lo que posibilita que una faceta considerada dentro del área a interceptar sólo lo haga parcialmente o bien que una faceta cuya reflexión en su centro no impacte en el área receptora, esté participando con un área menor. Para resolver esta dificultad es necesario combinar el método SHOT con una simulación computacional.
Recurriendo a la simulación por método Monte Carlo se analiza el mapa de intensidad del área que ocupa la ventana del calorímetro (figura 9). De la simulación se calcula que la radiación que impacta el modelo CAD del prototipo tiene una potencia de 792 W mientras que la potencia calculada dentro del área central de 0,09 m de diámetro es de 550 W. Finalmente, utilizando la ecuación (2), se obtiene una eficiencia óptica ηop = 0.69 ± 0,02.
Aunque el valor de ηop obtenido por el método de factor de intercepción no discrepa significativamente con el valor obtenido mediante simulación computacional (diferencia de 0,01) puede obtenerse más información analizando el mapa de flujo radiativo. Se observa cómo algunos espejos impactan parcialmente en el área central y cómo la forma central es circular debido a la superposición de gran cantidad de reflexiones de diferentes facetas. Este análisis resulta útil para el diseño del receptor ya que facilita la toma de decisión en las dimensiones de la ventana de entrada de los rayos solares, de modo de producir una relación de compromiso entre la energía recolectada y el tamaño del orificio de entrada al receptor que minimice las pérdidas térmicas.

Fig. 8 Puntos Pi sobre el objetivo en círculos rojos. El círculo azul delimita el área por donde ingresaban los rayos al calorímetro.
Comparación de los resultados de eficiencia óptica según el método utilizado
Los valores obtenidos utilizando los distintos métodos resultan ser similares como se observa en la tabla 1. Si bien pareciera existir una pequeña sobreestimación en el valor obtenido mediante el método del calorímetro de masa constante, lo cierto es que los valores de ηop determinados por los tres métodos se encuentran dentro del rango de incertidumbre de las medidas. Consecuentemente, la metodología del calorímetro de masa es considerada válida para concentradores de disco parabólico con características similares al analizado.Si bien la utilización de la metodología SHOT y su variante con simulación Monte Carlo permiten obtener mayor información sobre el concentrador, como por ejemplo conocer la distribución de los impactos o el mapa de intensidad de flujo en la zona focal (o en cualquier otro sitio del recorrido de los rayos), ambas metodologías resultan complejas en su ejecución y demandan una medición rigurosa.
Adicionalmente, la simulación Monte Carlo, que es un requisito para analizar geometrías no continuas, necesita de complejos algoritmos informáticos con cálculos específicos según la geometría del concentrador. En oposición, el método del calorímetro de masa constante resulta muy sencillo y requiere poca preparación previa, exigiendo solamente conocer las pérdidas térmicas del calorímetro. Las mediciones con el concentrador pueden realizarse en pocos días con resultados inmediatos.
Esta simplicidad y celeridad resulta excelente para la evaluación de concentradores prototipos que aún pueden necesitar modificaciones adicionales en su construcción.
Tabla 1 Valores de ηop obtenidos con diferentes metodologías
| Calorímetro masaconstante | SHOT factor Intercepción | SHOT + Simulación Monte Carlo | |
| ηop | 0,71 ± 0,02 | 0,70 ± 0,02 | 0.69 ± 0,02 |
En la figura 1, se muestran ηop admisibles para la aplicación del prototipo analizado como concentrador solar. Los valores ηop obtenidos podrían ser mayores si el alineamiento de algunas facetas fuera mejorado, esta observación surje al analizar el factor de intercepción, figura 8, donde se muestran impactos alejados de la circunferencia central.
Conclusiones
Es posible realizar un análisis de la eficiencia óptica obtenida con un prototipo experimental construido con espejos triangulares planos.
Un valor de ηop= 0,71 ± 0,02 se obtiene cuando se utiliza el método del calorímetro de masa constante, de realización rápida y simple.
El análisis del concentrador prototipo por el método SHOT evalúa el factor de intercepción γ y posibilita la determinación de la eficiencia óptica ηop= 0,70 ± 0,02. La aplicación de una simulación adicional por método Monte Carlo permite el análisis del mapa de flujo lumínico en la zona focal y proporciona un ηop = 0.69 ± 0,02.
Los valores obtenidos mediante los tres métodos resultan similares, con una variación de ± 0,03 entre ellos considerando su incertidumbre.
Es posible concluir que el método del calorímetro de masa constante resulta validado por los valores de ηop obtenidos por del método SHOT y su variante.
El método del calorímetro evalúa el concentrador del disco parabólico de forma sencilla, rápida y económica sin exigir demasiada preparación ni instrumental específico.
El método SHOT requiere un tiempo mayor para realizar la medición, puesto que es necesario numerar y caracterizar cada faceta del espejo concentrador. Además, necesitamayor procesamiento de datos mediante la utilización de herramientas computacionalescomplejas. Se concluye que, si bien el método SHOT modificado permite una mejor caracterización, la evaluación resulta lenta y laboriosa para prototipos susceptibles a modificaciones.
El concentrador prototipo analizado demuestra que es posible concentrar la luz solar utilizando espejos triangulares planos, mostrando un ηopadecuado para su uso como concentrador.