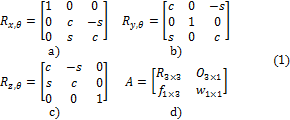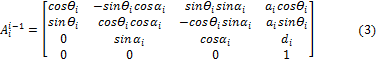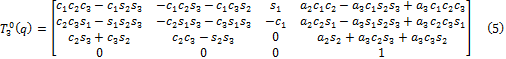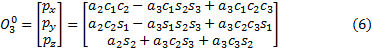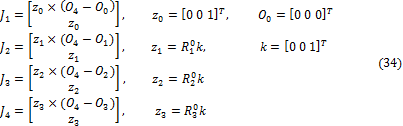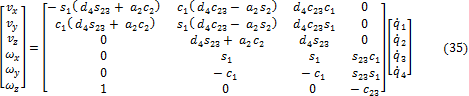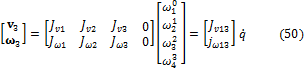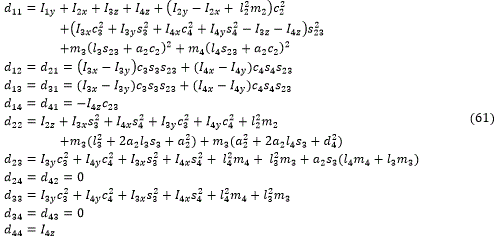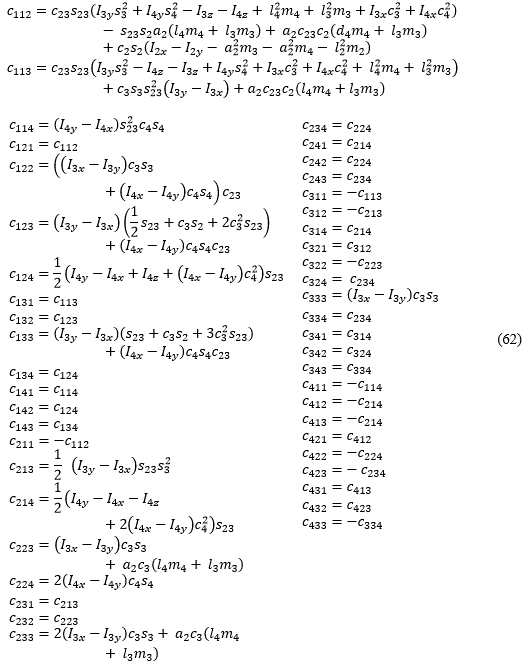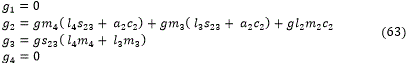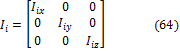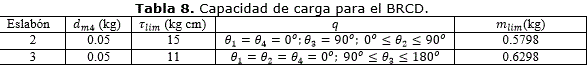ARTÍCULO ORIGINAL

 

 

Modelos cinemático y dinámico de un robot de cuatro grados de libertad

 

Kinematic and Dynamic Models for a 4-DOF robot

 

 

Eileen Cardoso ^I, Adel Fernández ^I, Sergio A. Marrero-Osorio ^II, Pablo F. Guardado ^III

^I Facultad de Automática y Biomédica, Departamento de Automática y Computación, Universidad Tecnológica de La Habana José Antonio Echeverría. La Habana, Cuba.
^II Facultad de Ingeniería Mecánica, Departamento de Mecánica Aplicada, Universidad Tecnológica de La Habana José Antonio Echeverría. La Habana, Cuba.
^III Ingeniería Mecatrónica, Instituto Tecnológico y de Estudios Superiores de Monterrey. Ciudad Juárez, Chihuahua, México.

 

 

---

RESUMEN

En este trabajo se obtienen los modelos cinemático y dinámico de un robot industrial de cuatro grados de libertad. El modelo cinemático se valida a través de una plataforma experimental, un microcontrolador y un programa de computadora de alto nivel. Con base en el modelo dinámico, se determina la capacidad de carga del manipulador. Se toman en cuenta las principales referencias bibliográficas actuales para el análisis de los robots industriales y se realiza una discusión de los resultados de varias simulaciones. Los modelos se pueden aplicar al diseño de mecanismos, componentes y controladores de robots de semejante morfología.

Palabras claves: manipulador robótico, robótica industrial, modelo cinemático, modelo dinámico.

---

ABSTRACT

In this work the kinematic and dynamic models of an industrial robot of four degrees of freedom is obtained. The kinematic model is validated through an experimental platform, a microcontroller and a high-level computer program. Based on the dynamic model, the load capacity of the manipulator are determined. The main references for the analysis of industrial robots are taken into account and a discussion of the results of several simulations is made. The models are applicable to manipulators with the same morphology in order to design mechanisms, components and controllers.

Key words: robotic manipulator, industrial robotic, kinematic model, dynamic model.

---

 

 

1.- INTRODUCCIÓN

 

El desarrollo tecnológico y la automatización de los procesos industriales han evolucionado a tal punto, que la mayoría de las grandes industrias, para disminuir los costes de producción y responder a la demanda, han tenido que actualizar sus procesos e insertar los robots industriales. Con estas máquinas se provee a los operadores de mecanismos autónomos que ayudan a ampliar sus capacidades físicas. Este fenómeno de crecimiento de la robotización industrial ha movido al mundo de la investigación para crear máquinas que puedan colaborar con el hombre en un mayor número de funcionalidades, mejor eficiencia energética, mayor capacidad de adaptación a las condiciones del entorno de trabajo, mayor seguridad en las operaciones y para producir bienes en un mínimo de tiempo [1,2].

El objetivo de este trabajo es la obtención y validación de los modelos cinemático y dinámico de un robot industrial de cuatro grados de libertad. Para validar el modelo cinemático se construyó una plataforma experimental que utiliza el brazo robótico S5 de carga/descarga modelo DIY de Sain Smart, que en lo delante denominaremos abreviadamente BRCD. Los modelos matemáticos a obtener son una herramienta útil para el diseño de robots que tengan esta configuración; considerando que la actividad de diseñar incluye el dimensionado y la selección de materiales para las uniones, brazos, soportes y otras partes; y también la selección de componentes como actuadores, cojinetes, pernos, y otras componentes. Desde el punto de vista de control, el modelo dinámico es utilizado para el control de posición, velocidad, fuerza entre otros. Es posible encontrar robots con esta morfología en procesos industriales de estibación, embalaje, soldadura, corte y pintura [3–5].

Los objetivos específicos del trabajo se enumeran a continuación:

1.       Obtener el modelo cinemático directo de posición, inverso de posición, directo de velocidad e inverso de velocidad para el BRCD.

2.       Obtener el modelo dinámico del BRCD.

3.       Validar de forma práctica y/o simulada cada uno de los modelos obtenidos.

4.       Determinar la capacidad de carga del BRCD.

La estructura del contenido es la siguiente: En la sección 1 se realiza una revisión de las metodologías para la modelación de los manipuladores robóticos que existen en la actualidad. En la sección 2 se establece el marco teórico para el análisis de la cinemática del manipulador robótico y se aplican las técnicas necesarias para resolver la cinemática de posición y de velocidad. En la sección 3 se describen los materiales y componentes que se utilizaron para la construcción de la plataforma experimental y se discuten los resultados prácticos y teóricos obtenidos de la validación del modelo cinemático. En la sección 3 se establece el marco teórico para la modelación dinámica, se obtiene el modelo y se valida a través de una simulación. Además, mediante un algoritmo se calcula la capacidad de carga del manipulador.

 

2.-CONCEPTOS BÁSICOS Y TRABAJOS RELACIONADOS

 

En la literatura se reportan varios métodos para enfrentar el proceso de modelación de un manipulador. La estructura mecánica del robot que es objeto de estudio es fundamental a la hora de seleccionar una metodología a seguir.

Para el análisis cinemático, en el caso de estructuras simples, se utilizan técnicas basadas en trigonometría y geometría elementales. En particular se aplican las propiedades de los ángulos interiores de los triángulos, el teorema de Pitágoras, las relaciones trigonométricas y la ley de los cosenos. El álgebra lineal es otra de las ramas fundamentales. En casi todas las etapas de modelación se necesita efectuar operaciones matriciales y vectoriales, aplicadas a los movimientos de traslación y rotación de un cuerpo rígido en el espacio.

Es de vital importancia el dominio de las matrices de rotación dadas en (1a, b, c), donde sin(θ) = s y cos(θ) = c. Estas matrices permiten expresar las coordenadas de un vector sobre un marco de referencia, en función de otro marco de referencia que se encuentre rotado con respecto al primero [6,7]. La rotación de un marco de referencia sobre el eje x un ángulo ϴ se calcula con la matriz de rotación R_x,θ, sobre al eje y con la matriz R_y,θ, mientras que sobre eje z con R_z,θ.

En robótica es común utilizar la denominada matriz de transformación homogénea [6–8]. Esta es una matriz de 4×4 que contiene información, tanto de la orientación como de la traslación de un marco de referencia con respecto a otro, su estructura se presenta en (1d), donde R_3×3 es una matriz de rotación, f_1×3 es un vector fila que puede presentar un cambio de perspectiva entre los marcos, en robótica este vector es nulo, w_1×1 representa un cambio de escala entre marcos de referencia, en robótica este valor es la unidad. Finalmente, O_3×1 es la distancia entre los orígenes de los marcos de referencia.

Se destaca que a la multiplicación de n matrices de transformación homogéneas se le denomina composición, y permite transformar las coordenadas de un punto sobre un marco de referencia, a lo largo de n marcos de referencia rotados y desplazados entre sí [6].

La definición de un cuerpo en el espacio es relativamente fácil utilizando coordenadas cartesianas. Sin embargo, definir la orientación de un cuerpo en el espacio es algo más complejo, para ello se utiliza la representación de Euler, la representación roll-pitch-yaw o la representación por eje/ángulo [1,6,8].

Otro método matemático que se aplica en el análisis cinemático es el método de los cuaternios. El término cuaternios parte de una extensión de los números complejos y permite determinar la orientación de un objeto en el espacio tridimensional [9,10].

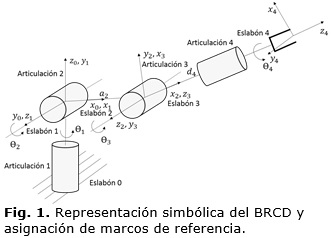
En el análisis de un manipulador robótico se debe asignar un marco de referencia a cada eslabón que conforma su cadena cinemática (Figuras 1 y 2). El primer marco representa la base del manipulador y el último su punto terminal (PT). Aunque los marcos pueden asignarse arbitrariamente es aconsejable seleccionar un convenio para la localización de los marcos, esto favorece la modelación del manipulador y la eficiencia computacional. La convención fundamental para la asignación de marcos de referencia es la de Denavit y Hartenberg (DH)[6,7].

Para la modelación cinemática y dinámica es necesario aplicar el convenio DH de forma tal que se describa el robot en función de los parámetros estáticos de los eslabones y las variables de cada articulación. Estas variables pueden ser de desplazamiento o de rotación. La modelación se divide en cinco partes:

Modelo cinemático directo de posición: determina la posición del PT a partir de las variables de articulación [8–11].

Modelo cinemático inverso de posición: determina el valor de las variables de articulación en función de la posición del PT deseada. Su solución puede obtenerse mediante una relación matemática explícita o por medio de procedimientos numéricos iterativos [8,10,11]. Para casos de robots con 6 GDL se recomienda el uso del método de desacoplamiento cinemático. Este método permite resolver los tres grados de libertad dedicados al posicionamiento de manera independiente a los tres grados de libertad dedicados a la orientación [6]. Los métodos numéricos tienen el inconveniente de que su convergencia no siempre está garantizada.

Modelo cinemático directo de velocidad: determina la velocidad del PT a partir de las velocidades de las variables de articulación. Para obtener este modelo se debe definir la matriz jacobiana del manipulador. Esta puede considerarse como la versión vectorial de la derivada ordinaria de una función escalar [8,11].

Modelo cinemático inverso de velocidad: determina las velocidades de las variables de articulación a partir de la velocidad del PT deseada. Este modelo es fácil de obtener si se calcula la inversa de la matriz jacobiana. En caso de que la matriz jacobiana sea no cuadrada, deberá utilizarse la denominada pseudoiversa [8,11].

Modelo dinámico: es imprescindible para diseñar y evaluar la estructura mecánica del robot, así como dimensionar los actuadores y otras partes. Para la resolución de este modelo se usan métodos y procedimientos basados en la mecánica Newtoniana y Lagrangiana [6,7,12]. La formulación del modelo dinámico por el método Euler–Lagrange fue presentado por Uiker en 1965. Este modelo conduce a unas ecuaciones finales bien estructuradas donde aparecen de manera clara los diversos pares y fuerzas que intervienen en el movimiento (inercia, centrifuga, Coriolis, gravedad). ^.La desventaja del modelo radica en que es ineficiente desde el punto de vista computacional, pues el número de operaciones crece con una potencia de cuatro en relación con el número de grados de libertad que presente el robot [6,8,13,14]. Otro método utilizado para la obtención del modelo dinámico es mediante la formulación de Newton-Euler [15]. Para usar este método se parte de la ley de conservación de par y fuerza. Se aplica habitualmente en robots de 6 grados de libertad, ya que el coste computacional es mucho menor en comparación con el método Euler–Lagrange.

Una vez que se cuenta con los modelos del manipulador, para su puesta en práctica es importante tener en cuenta la trayectoria que seguirá dentro de su espacio de trabajo[1,7,8,16,17] y el estudio de las singularidades del mismo[1,8,18]. El análisis de las singularidades tiene que ver con determinadas posturas del manipulador que pueden incidir en un desempeño inadecuado de los sistemas de control.  

 

3.- MODELO CINEMÁTICO

 

La Figura 1 muestra la representación simbólica del BRCD, sobre esta representación aparecen los 5 marcos de referencias necesarios para modelar el brazo. Note que el BRCD tiene cuatro grados de libertad, debido a sus cuatro articulaciones rotacionales y sus cinco eslabones, contando la base. Este manipulador se denomina angular o articulado y posee un área de trabajo esférica. De acuerdo con el convenio DH los marcos de referencia se colocan considerando las siguientes pautas:

1.       Las articulaciones se enumeran desde i = 1 hasta n, siendo i, la i-ésima articulación.

2.       Los ejes z_i se colocan a lo largo de la siguiente articulación i+1.

3.       Si z_i y z_i-1 se interceptan, el origen del marco x_iy_iz_i se sitúa en ese punto. Esto sucede tanto entre los marcos x₀y₀z₀ y x₁y₁z₁, como entre los marcos x₂y₂z₂ y x₃y₃z₃.

4.       El eje x_i se toma a lo largo de la normal común entre los ejes z_i y z_i-1 con dirección desde la articulación i hacia i+1.

5.       El eje y_i se toma de forma que se complete el marco.

6.       Para la base (marco x₀y₀z₀) solo se especifica la dirección del eje z₀ y se escoge x₀ y y₀ a conveniencia.

7.       Para el último eslabón no hay marco i+1. En general la articulación n es de rotación y el eje z_n se escoge alineado con z_n-1.

A partir de estos marcos de referencia se obtienen los cuatro parámetros del manipulador:

      •   Largo del eslabón a_i: distancia entre los ejes z_i-1 y z_i a lo largo del eje x_i.

      •   Distancia de articulación d_i: distancia entre los ejes x_i-1 y x_i a lo largo del eje z_i-1.

      •   Ángulo de articulación θ_i: rotación requerida del eje x_i-1 sobre z_i-1 para quedar paralelo a x_i. Se usa la regla de la mano derecha para conocer el sentido.

      •   Ángulo de torsión α_i: rotación requerida del eje z_i-1 sobre x_i para quedar paralelo a z_i.

En la Tabla 1 se muestran los datos particulares del BRCD, se observan datos constantes que representan las dimensiones de los eslabones y los ángulos de torsión entre las articulaciones 1 y 2, y las articulaciones 3 y 4 respectivamente. Note que en cada fila de la tabla solo hay una variable, en este caso el ángulo de rotación de cada una de las articulaciones θ_i.

3.1.- MODELO CINEMÁTICO DIRECTO DE POSICIÓN

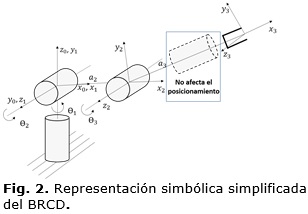
Para conocer la posición del PT se puede simplificar el esquema mostrado en la Figura 1, ya que es obvio que la articulación 4 no influye en la posición final del manipulador. La Figura 2 muestra la nueva representación y la Tabla 2 los parámetros asociados.

Note que la Tabla 2 disminuye en una fila con respecto a la Tabla 1, lo cual repercutirá en la cantidad de operaciones a realizar para calcular la cinemática directa del manipulador. Al eliminar la articulación 4 no hay ángulo de torsión entre 2 y 3 y la distancia de articulación d₄ se convierte en el largo de eslabón a₃. 

El convenio DH indica que cada fila de la Tabla 2 debe ser convertida en una matriz homogénea A_i^i-1 que se obtiene de la composición de 4 matrices homogéneas básicas según la siguiente ecuación:

donde:

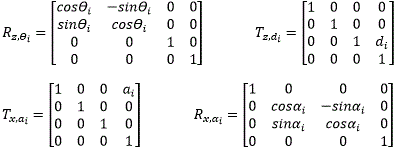
La matriz R_z,_ϴi indica rotación en el eje z un ángulo ϴ_i, la matriz T_z,di indica traslación sobre el eje z una distancia d_i, la matriz R_x,αi indica rotación en el eje x un ángulo α_i, mientras que la matriz  T_x,ai indica traslación sobre el eje x una distancia a_i. Al efectuar estas operaciones matriciales se tiene como resultado la ecuación (3), que es una matriz homogénea en función de ϴ_i ya que el resto de los parámetros son constantes.

A partir de la ecuación anterior se obtienen las matrices asociadas a cada eslabón:

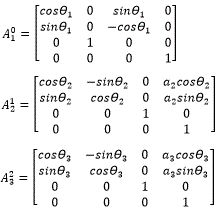
El primer resultado A₁⁰ brinda información de la orientación del marco x₁y₁z₁ referido al marco base. Ambos marcos están superpuestos uno encima del otro, pero con una orientación diferente. El segundo marco está trasladado una distancia [a₂cosθ₂ a₂sinθ₂ 0]^T respecto del primer marco y también con una orientación diferente a este. Por último, el marco x₃y₃z₃ está desplazado [a₃cosθ₃ a₃sinθ₃ 0]^T respecto del segundo marco y también con una orientación diferente.

La composición de estas matrices homogéneas según la ecuación (4) permite encontrar las coordenadas del PT del manipulador en función del marco base y por tanto la posición de este punto respecto a la base.

Al vector q = [θ₁ θ₂ θ₃]^T   se le denomina vector de coordenadas generalizadas. El resultado de esta operación es:

Donde cosθ_i= c_i y sinθi = s_i. De la matriz (5) se obtiene el modelo cinemático directo de posición para el BRDC.  La posición del PT es:

Mientras que su orientación final con respecto a la base está dada por la matriz de rotación:

Ejemplo 1: Para θ₁=30°, θ₂=45°, θ_­3=60°, la posición alcanzada por el PT fue de (2.6195, 1.5123, 23.8454). En la Figura 3 se observa la representación gráfica del manipulador para estos ángulos.

3.2.- MODELO CINEMÁTICO INVERSO DE POSICIÓN

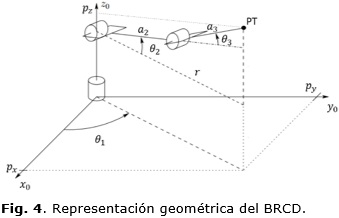
Resolver el modelo cinemático inverso, o sea, obtener los valores de q a partir de O₃⁰ implica resolver el sistema de tres ecuaciones y tres incógnitas que se observa en (6). Sin embargo, estas ecuaciones trigonométricas no son sencillas de resolver, la mayor parte de las veces hay más de una solución posible e incluso infinitas soluciones. Para el BRCD se aplica el método geométrico que se describe a continuación.

De la Figura 4 se observa que el ángulo θ₁ se obtiene de la ecuación trigonométrica:

Si p_y y p_x son nulos, se obtienen infinitas soluciones para θ₁, esto indica que el PT se encuentra sobre el eje z de la base. En este caso se puede escoger un valor arbitrario o simplemente mantener el valor anterior.

Para calcular cualquier ángulo θ, en lugar de usar la ecuación θ = tan^-1(y/x), resulta más práctico utilizar la función:

Esta función se denomina arco-tangente de dos argumentos y utiliza los signos de x e y para seleccionar de forma automática el cuadrante del ángulo θ, por ejemplo atan2(1,-1) = -π/4, mientras que atan2(-1,1) = +3π/4.  La mayoría de los asistentes matemáticos y librerías de los lenguajes de programación modernos cuentan con ella. Luego:

A partir de la Figura 4 y el teorema de Pitágoras se plantea la ecuación:

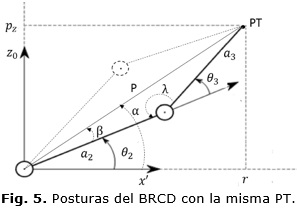
Para obtener los valores de θ₂ y θ₃ se utiliza la construcción geométrica que se muestra en la Figura 5. La misma muestra dos posibles posturas del BRCD para alcanzar la misma posición final.

De un análisis geométrico se obtienen las siguientes relaciones:

De acuerdo con el teorema de Pitágoras:

Aplicando la ley de cosenos y (12) se tiene:

Despejando cosθ₃ en (14) y combinando con (13) se obtiene:

Combinando (16) y (17) en (9) se obtiene:

Si se toma el valor positivo de θ₃ se selecciona la postura inferior que se muestra en la Figura 5, por el contrario si se toma el valor de θ₃ con signo negativo se selecciona la postura superior.

El valor de θ₂ se obtiene:

Donde β se calcula a partir de (13) y (15):

Y α se calcula usando (9) y (11):

Las ecuaciones (10), (18) y (19) conforman el modelo cinemático inverso de posición para el BRCD. Estas ecuaciones quedan en función de los parámetros constantes del manipulador a₂, a₃ y el PT dado por las coordenadas (p_x, p_y, p_z).

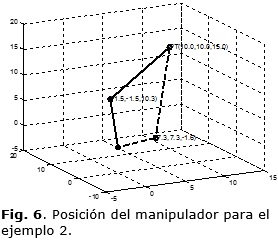
Ejemplo 2: Si se desea que el PT esté en la posición (10, 10, 15).  La primera solución está dada por los ángulos: θ₁=45°, θ₂ = -8.6°, θ₃ = 85.7°; mientras que la segunda solución por: θ₁ = 45°, θ₂ = 102°, θ₃ = -85.7°. La Figura 6 muestra la representación en 3 dimensiones para las dos posturas posibles del BRCD.

Vale indicar que para un robot con menos de 6 grados de libertad no es posible especificar cualquier orientación deseada para el PT. La orientación de este punto queda determinada cuando se escoge una posición en el espacio de trabajo para este. Sin embargo, en el BRCD es posible variar esta orientación final en un grado de libertad, utilizando la articulación 4. En la plataforma experimental construida se manipula esta articulación de forma independiente una vez que se alcanza la posición deseada.

3.3.- MODELO CINEMÁTICO DIRECTO DE VELOCIDAD

Para calcular la cinemática directa de velocidad se debe tener en cuenta que cada articulación rotacional aporta velocidad angular y velocidad lineal al PT. El aporte de cada articulación depende de la posición del robot para cada instante de tiempo t. La ecuación (22) muestra la forma correcta de adicionar las velocidades angulares en un manipulador robótico [7]. 

En (22) n es la cantidad de articulaciones del manipulador. Note que las velocidades angulares solo pueden sumarse si están referidas al mismo marco de referencia. El término R⁰_i-1ω_i^i-1 permite adicionar la velocidad angular ω_i^i-1 que aporta la articulación i, por medio de su actuador, al PT. Para ello se multiplica esta cantidad por la matriz de rotación R⁰_i-1 del marco x_i-1y_i-1z_i-1 respecto de la base.

La representación de la velocidad lineal y angular del PT se escribe en forma vectorial Ẋ = [v_x v_y v_z ω_x ω_y ω_z]^T.  El modelo matemático de la cinemática de velocidad directa del manipulador implica obtener la matriz jacobiana J de la ecuación (23).

Donde I03 = [I03₁ I03₂ I03₃ I03₄]^T es el vector de velocidades generalizadas del BRCD. En la práctica sus valores son conocidos si se colocan sensores de velocidad en las articulaciones. Note que la matriz J debe ser 6×4, donde cada columna J_i de 6×1 se asocia a una de las articulaciones del manipulador:

A su vez cada columna J_i se divide en dos vectores, que se relacionan con la velocidad lineal y la velocidad angular:

Los valores de J_ωi se pueden inferir directamente de la ecuación (22). Para ello se reescribe esta ecuación de la siguiente forma:

La componente J_vi está relacionada con la velocidad lineal, en el análisis se parte de la ecuación clásica:

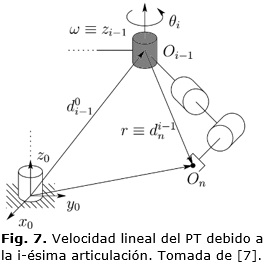
Donde v es el vector velocidad lineal, ω el vector velocidad angular y r = d_n^i-1, o sea la distancia entre el origen del marco de referencia de la i-ésima articulación O_i-1 y el marco de referencia del PT, O_n, según se puede ver en la Figura 7. Reescribiendo (29) en función de las variables de articulación se tiene:

Recuérdese que para obtener la velocidad con respecto a la base se debe multiplicar por la matriz de rotación del eje asociado hasta la base. De (30), (27) y la Figura 7 se tiene:

Y por tanto

En (24) los términos J_i se obtienen de la siguiente forma:

Los valores de R_i⁰ y O_i se calculan a partir de las ecuaciones de la cinemática directa desde la base hasta la articulación i. Por ejemplo, las variables asociadas con el segundo eslabón y basados en la Tabla 1, son:

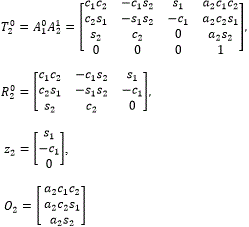
El resultado final es:

Donde s₂₃ = sin(θ₂ + θ₂), c₂₃ = cos(θ₂ + θ₂).

3.4.- MODELO CINEMÁTICO INVERSO DE VELOCIDAD

Para obtener el modelo cinemático inverso de velocidad se debe invertir la ecuación (23) o la ecuación (35)

Esto solo se puede lograr si la matriz J es invertible. Para un manipulador de menos de seis articulaciones, esto es posible si y solo si X se encuentra en el rango del Jacobiano [1,7]:

La solución se puede obtener usando la pseudoinversa de la matriz jacobiana J⁺ de forma tal que se cumpla la condición

J⁺J=I [1,7]. Una forma para obtener la pseudoinversa es J⁺ = (J^TJ)^-1J^T. Por tanto, si se tiene la matriz jacobiana por la ecuación (35) también se tiene su modelo cinemático inverso:

Las ecuaciones (35) y (38) conforman el modelo cinemático directo e inverso de velocidad respectivamente para el BRCD.

3.5.- VALIDACIÓN DEL MODELO CINEMÁTICO

Para validar teóricamente el modelo cinemático de posición, basta con obtener los ángulos de articulación θ₁, θ₂, θ₃ del modelo cinemático inverso de posición para una o varias posiciones deseadas del PT P_f(x, y, z) y luego comprobar, con el modelo cinemático de posición directo que estos ángulos brindan como resultado la misma posición P_f(x, y, z). Sin embargo, esto no implica que en la práctica los modelos queden validados.

La Plataforma de Validación Experimental (PVE) que se construyó está formada por los siguientes componentes:

1.       Brazo robótico S5 de carga/descarga modelo DIY de Sain Smart (BRCD): posee cuatro grados de libertad y una pinza de agarre. Los actuadores son 4 servomotores modelo MG996R y uno modelo DS3218. Los primeros con un torque máximo de 11 Kg.cm, y el segundo hasta 15 Kg.cm, ambos con un voltaje de alimentación que puede variar entre 4.8 V y 7.2 V.

2.       Microcontrolador Arduino UNO: dotado con un procesador Atmega 328, posee 6 salidas PWM, de las cuales 5 se utilizan para manipular los servomotores del BRCD.

3.       Fuente de alimentación 5V, 2.5 A.

4.       Programa de computadora de alto nivel desarrollado en C++.

El programa de alto nivel, recibe del usuario la posición final que desea colocar en el BRCD, permite manipular la orientación del cuarto eslabón de forma independiente y también abrir y cerrar la pinza de agarre. Con estos datos calcula la cinemática inversa de posición y envía los resultados, utilizando comunicación serie, al Arduino UNO. En el Arduino se recibe la información, se calcula la trayectoria desde el punto actual hasta el siguiente y se manda la señal correspondiente a cada servomotor a través de las salidas PWM asociadas.

3.5.1- VALIDACIÓN DEL MODELO CINEMÁTICO DE POSICIÓN

Una vez que la PVE está en marcha se puede formular la siguiente hipótesis de validación: si se le ordena al BRCD que alcance una serie de posiciones dentro de su espacio de trabajo, y este logra llegar a las posiciones esperadas entonces el modelo se puede considerar adecuado. La hipótesis se comprueba mediante el experimento que se describe a continuación.

Para analizar la posición que alcanza el PT con respecto al resultado del modelo, se calculan los errores cometidos [19]. Por definición si se mide una magnitud cuyo valor verdadero es M_v y cuyo valor medido es M, el error absoluto cometido es:

Por otro lado, el error relativo se define como:

Para realizar las mediciones se consideró una orientación de la muñeca fija y la pinza cerrada. En la Tabla 3 aparece la medición de cada una de las posiciones reales alcanzadas por el BRCD a partir de los resultados obtenidos por el modelo cinemático directo de posición. Para la primera medición el BRCD parte de su posición inicial, para el resto de las mediciones que se realizaron el punto de partida es la postura anterior. Además, se presentan los errores absolutos cometidos con respecto a los ejes x, y, z. Los errores se calcularon considerando como valor verdadero los valores de posición que se obtuvieron aplicando el modelo cinemático inverso de posición.

Varias mediciones tienen un error absoluto muy superior al error medio en los tres ejes de coordenadas. Para verificar estas mediciones se realiza un estudio de dispersión. La dispersión se produce cuando se obtienen valores diferentes en sucesivas tomas de datos. Lo habitual, para enfrentar este fenómeno, es realizar tres repeticiones de la medición y comprobar el valor de la dispersión, la cual se calcula como:

Para el análisis de la dispersión se consideraron las mediciones 5, 7, 12. En estas mediciones los errores absolutos superan o igualan, en los tres ejes, la media de los errores. Primero se hicieron tres repeticiones de estas mediciones, pero la dispersión calculada fue superior a 1mm, sensibilidad del aparato de medición (regla), por lo tanto, se procedió a incrementar el número de repeticiones a seis. En la Tabla 4 se observa que con seis repeticiones se logró alcanzar dispersiones entre un 2 y un 8% lo que se considera correcto para esta cantidad de repeticiones. En este caso el valor de la medición que se considera es la media aritmética de las seis mediciones tomadas [19]. Utilizando el método del análisis de la dispersión se logró reducir el error absoluto de las mediciones.

Durante este experimento se observó que los errores de medición, además de ser provocados por imprecisiones humanas, también se afectan por: la sensibilidad del instrumento de medición, errores estructurales del manipulador y la sensibilidad de los servomotores. Durante los experimentos y la calibración de los servomotores se observó que los servomotores tienen una sensibilidad de ±1°, lo cual equivale a 0.01745 radianes. Como error de la estructura mecánica del BRCD se observó que cuando las articulaciones se posicionan, el eslabón tres no permanece en la posición fijada, tienen un pequeño desplazamiento en el sentido negativo del eje z del marco de referencia base, producto del propio peso del eslabón.

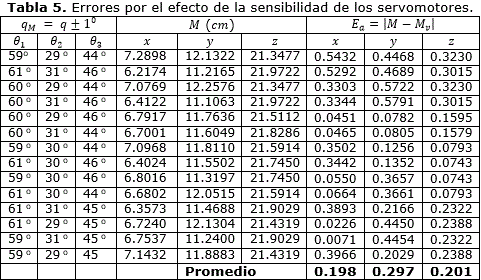
Para analizar el efecto de la sensibilidad de los servomotores sobre el error en la medición, se realiza una prueba donde se modifica el vector de coordenadas generalizadas q, teniendo en cuenta la sensibilidad de los servomotores. Esto implica:

q_M = q±1°

Donde qM es el vector de coordenadas generalizadas modificado y q = [60° 30° 45°] es el valor escogido para la prueba.El valor verdadero del PT para q es M_v = [6.7466, 11.6854, 21.6707]. En la Tabla 5 se puede apreciar los errores absolutos de posición provocados por los servomotores.

Luego de este estudio podemos concluir que el efecto de la sensibilidad de los motores puede afectar entre 0.2 - 0.3 cm la posición del PT.

Los experimentos realizados demuestran que el modelo cinemático de posición es válido pues las mediciones obtenidas con los ángulos sugeridos por el modelo, se aproximan a la posición esperada con un error absoluto promedio de 0.8 cm. Si se tiene en cuenta que el área de trabajo es una esfera de 27.5 cm, el error relativo respecto del área de trabajo es de 2.9%. Este resultado, según la opinión de los autores, es aceptable para la PVE empleada, que se basa en un manipulador experimental no profesional.

3.5.2- VALIDACIÓN DEL MODELO CINEMÁTICO DE VELOCIDAD

Al no contar con sensores de velocidad, la validación se realizó de forma indirecta mediante la medición del tiempo y desplazamiento angular. Los datos se obtuvieron utilizando una cámara de video con una precisión de 0.03 segundos. Para analizar cómo se propaga el error relativo de la medición del tiempo sobre la velocidad angular E_r(ω) se tiene:

Donde E_a(θ) es el error absoluto del desplazamiento angular, θ_M es el desplazamiento angular medido, E_a(t) el error absoluto del tiempo y t_M es el tiempo medido. 

El experimento se realizó utilizando la PVE para cinco velocidades diferentes sobre una trayectoria lineal de 90° en la articulación 1. Para cada una de las velocidades impuestas se realizaron 6 repeticiones, tomando el mayor y menor tiempo. Para el cálculo del error relativo E_r(ω)se tomó en cuenta un error de desplazamiento angular E_a(θ) =1° = π/180 rad. Al considerar θ = 90° como valor verdadero entonces E_r(θ) = 1°/ (90°±1°) = 0,011. La Tabla 6 refleja los resultados obtenidos, las tres primeras columnas contienen los valores verdaderos utilizados en cada medición.

Note que los errores absolutos de tiempo están en el orden de la precisión de la cámara y como se están utilizando intervalos de tiempo pequeños no cabe duda que esta precisión altera los resultados. También se puede apreciar que los E_r(ω) más elevados corresponden con el análisis realizado con los tiempos máximos, y para este caso particular aumenta con la velocidad. Cuando E_a(t) es cero el E_r(ω)se afecta por el error de posición en 1.1 %.

Por otro lado, la velocidad lineal se relaciona con la velocidad angular por v = ωr, donde r es el radio desde el eje de rotación hasta el PT. Para este experimento se consideró una postura fija, donde el radio es el mismo en todas las trayectorias. Luego, el error relativo de la velocidad lineal es:

Esto significa que el error absoluto de la velocidad lineal es proporcional al error relativo de la velocidad angular. Por lo tanto, dado que los resultados del experimento arrojaron errores relativos de velocidad angular aceptables se considera que el modelo cinemático de velocidad obtenido para el BRCD es correcto.

Desde el punto de vista teórico, la validación de la ecuación (35) implica la validación de la matriz jacobiana. Uno de los resultados que brinda esta matriz es el conocimiento de las denominadas singularidades del robot [1,7]. Las singularidades representan:

a)       Límites del espacio de trabajo.

b)       Posturas donde se pierden grados de libertad del manipulador.

c)       Velocidades limitadas del efector final, representan velocidades no limitadas de las articulaciones.

d)       Corresponden a posturas donde hay infinitas soluciones en la cinemática inversa de posición.

Si se comprueban estas singularidades a partir (35) se estaría validando la matriz jacobiana obtenida. Para ello se debe obtener el determinante de la sub-matriz 3×3 que se encuentra en la parte superior izquierda. Note que esta sub-matriz contiene información del desplazamiento del manipulador, ya que relaciona las velocidades lineales del PT, a partir de las velocidades angulares de las tres primeras articulaciones. Las singularidades se presentan cuando esta sub-matriz pierde rango, o sea, cuando su determinante es 0. Realizando los cálculos correspondientes se obtiene la ecuación:

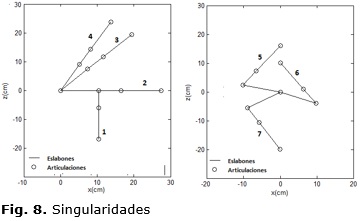
Es fácil verificar que para θ₃ = π/2 + kπ, k ∈ ℤ, se anula la ecuación (44). Esta condición corresponde a las singularidades señaladas por a) y b), ya que el manipulador solo puede moverse en un plano y siempre recorre el límite de su espacio de trabajo. La Figura 8 muestra el plano xz para diferentes posturas del BRCD, las articulaciones 1 y 2 están superpuestas en el origen de coordenadas, el resto se distinguen de forma individual. La postura inicial θ₁ = θ₂ = θ₃ = θ₄ = 0 se representa por 1, mientras que las posturas representadas por 2, 3 y 4, están dadas por valores de θ₃ = π/2 y valores de θ₂ = 0, θ₂ = π/4, θ₂ = π/6 respectivamente. En los últimos tres casos, sin importar el valor de θ₂, el PT se encuentra en el borde de su espacio. Aquí la articulación 4 no influye en la posición y si se varía θ₁, saliendo o entrando del plano, la condición de límite tampoco se pierde.

La solución del segundo factor en (44) es más complicada. Algunas soluciones particulares, obtenidas mediante procedimientos numéricos son:

Ⅰ. θ₂ = 2.9096, θ₃ = -0.4129 rad

Ⅱ. θ₂ = -0.3844, θ₃ = 4.1356 rad

Ⅲ. θ₂ = -2.5868, θ₃ = 3.1395 rad

Las posturas para las soluciones Ⅰ, Ⅱ y Ⅲ se muestran en la Figura 8 representadas por 5, 6 y 7 respectivamente. En todos los casos la cinemática inversa de posición da como resultado infinitas soluciones para θ₁, ya que el PT se encuentra sobre el eje z. En estas soluciones se está en presencia de las singularidades del tipo b), c) y d); se pierde un grado de libertad, ya que al variar θ₁ no es posible mover el PT ni modificar su velocidad lineal.

 

4- MODELO DINÁMICO

 

El método utilizado para obtener el modelo dinámico del manipulador robótico está basado en las denominadas ecuaciones de Euler-Lagrange que se presentan a continuación:

Donde, q_i son las coordenadas generalizadas, τ el vector de fuerzas o pares aplicados a los eslabones, mientras que K y P son la energía cinética y la energía potencial del manipulador respectivamente.

La ecuación (47) muestra que la energía cinética tiene una componente de traslación lineal K_l más otra componente rotacional K_r.

Desde el punto de vista vectorial K_l se obtiene como:

Mientras que K_r se obtiene como:

Siendo m la masa del cuerpo e I la matriz 3×3 denominada tensor de inercia.

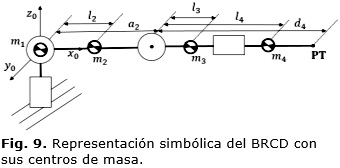
Cada elemento de la cadena cinemática del BRCD aporta energía de traslación y de rotación al manipulador. Para el análisis se considera la masa de los eslabones concentrados en su centro de gravedad tal y como se muestra en la Figura 9. El tensor de inercia I es referido a este punto también.

A continuación se analiza la energía del 3er eslabón y a partir de la misma se puede generalizar el resultado para el resto de los eslabones. La ecuación (50) obtiene la velocidad lineal y angular del centro de masa del tercer eslabón en forma vectorial. Note que el cuarto eslabón no aporta energía de traslación o rotación al tercero, mientras que los dos primeros si lo hacen. Por lo tanto, la matriz jacobiana solo considera términos no nulos hasta el 3er eslabón.

La ecuación (51) permite calcular la energía total del eslabón.

El producto R₃⁰I₃(R₃⁰)^T permite expresar el tensor de inercia respecto del marco de referencia en la base. Al sustituir en (51) las variables v₃ y ω₃ en términos de las coordenadas generalizadas se tiene:

La energía potencial del tercer eslabón en forma vectorial se expresa:

Donde 𝑔󠄐 es la󠄐 aceleración de la gravedad y el punto p_c3 se refiere a la posición en el espacio del centro de gravedad del tercer eslabón con respecto a la base. La gravedad siempre actúa referida al eje z del marco base.

De la misma forma se obtienen la energía cinética y potencial para cada eslabón, dando lugar a las expresiones:

La ecuación (54) puede ser escrita en forma compacta:

Donde D es una matriz simétrica de 4×4 que se conoce como matriz de inercias. Sustituyendo (55) y (56) en (46) y luego en (45) es posible obtener el modelo dinámico del BRCD. La solución general de la ecuación (45) para manipuladores robóticos se expresa en función de tres términos:

Donde:

D: matriz de inercia formada por elementos d_ij, 1 ≤ i ≤ 4; 1 ≤ j ≤ 4

C: matriz de términos de Coriolis y de las fuerzas centrífugas (4×4). Relacionada con la interacción física de los eslabones. Sus elementos c_kj, 1 ≤ k ≤ 4; 1 ≤ j ≤ 4 se calculan de la siguiente forma:

Los términos c_ijk se denominan símbolos de Christoffel y la forma de obtenerlos es:

G: vector de gravedad (4×1). Sus elementos 𝑔󠄐_i; 1 ≤ i ≤ 4, se obtienen:

El modelo dinámico del BRCD fue obtenido con ayuda de un asistente matemático. Para la matriz de inercias D(q) se tiene:

Los símbolos de Christoffel son:

Mientras que los términos asociados al vector de gravedad:

Las variables l_i son la distancia desde la articulación i hasta el centro de gravedad del i-ésimo eslabón. s₂₃ = sin(θ₂ + θ₂), c₂₃ = cos(θ₂ + θ₂). Además, se ha considerado que los tensores de inercia I_i asociados con el centro de masa de cada eslabón i tienen la forma general:

4.1- VALIDACIÓN DEL MODELO DINÁMICO

El modelo dado por la ecuación (57) se puede utilizar para conocer las fuerzas y pares que se aplican sobre cada eslabón mientras el manipulador sigue determinada trayectoria. No es posible medir en la PVE, de forma directa o indirecta las fuerzas y torques que se ejercen sobre los eslabones del manipulador. En este caso, la validación se hará realizando una simulación que permitirá corroborar las siguientes hipótesis:

1.       Los pares de los eslabones 1 y 4 deben ser inferiores a los eslabones 2 y 3 ya que los últimos actúan en contra de la gravedad.

2.       El par máximo del segundo y tercer eslabón debe presentarse cuando estos están en posición horizontal, ya que la fuerza de gravedad se aplica completamente perpendicular al eslabón.

3.       El par mínimo en el segundo y tercer eslabón debe presentarse cuando el eslabón se encuentre en posición vertical, ya que la incidencia de la fuerza de gravedad es la menor posible.

En la Tabla 7 se encuentran los datos referentes a las masas y tensores de inercia del BRCD que se utilizaron en la simulación.

La posición, velocidad y aceleración de cada articulación durante la simulación se muestra en la Figura 10. Los resultados de la simulación se muestran en la Figura 11; esta se divide en tres partes, a la izquierda se encuentran las gráficas de los pares o torques que se ejercen sobre los eslabones 1-4 y 2-3, mientras que a la derecha se representan las posiciones relevantes, en el plano xz, del BRCD para esta trayectoria.

Note que cada una de las hipótesis planteadas se cumple cabalmente. El BRCD parte de la posición inicial identificada con el punto 1. El par máximo en el segundo eslabón se produce cuando el centro de gravedad del eslabón 2 está alineado en la horizontal con el centro de gravedad del sistema que forman los eslabones 3 y 4, o sea cuando la fuerza de gravedad actúa en su dirección perpendicular, esto se representa en el punto 2 de las gráficas. Por el mismo motivo, el par máximo del tercer eslabón se produce cuando este se encuentra en la horizontal, es decir el punto 3.  El punto 4 representa la posición vertical, los pares de los eslabones 2 y 3 se anulan, pues no es necesario contrarrestar la fuerza de gravedad y, además, la aceleración angular debido al movimiento de las articulaciones es cero (Figura 10). Note que la posición final, dada por el punto 5, es similar a la posición inicial, pero en sentido opuesto. Por tanto, el valor del par en todos los eslabones es igual en magnitud a las del punto 1, pero de signo contrario.

4.2- OBTENCIÓN DE LA CAPACIDAD DE CARGA DEL MANIPULADOR

Utilizando el modelo dinámico se puede determinar la capacidad de carga del manipulador [20]. Es evidente que su capacidad está dada por los pares que se ejercen en los eslabones 2 y 3, pues como ya se dijo, son los que actúan en contra de la fuerza de gravedad. Para calcular este valor se ha utilizado el algoritmo heurístico que se muestra en el Listado 1. En la evaluación del modelo se considera la ecuación (57) expresada en función de la masa del cuarto eslabón (m₄), y la distancia desde la articulación 4 hasta el centro de gravedad del cuarto eslabón l_eq. El centro de gravedad debe ser calculado de acuerdo con la masa adicional que sostiene la pinza. La ecuación (65) tiene en cuenta el análisis anterior.

En el algoritmo, la masa adicional d_m4 se aumenta hasta que se llegue al par máximo τ_lim que puede ejercer el servomotor.

Los resultados obtenidos se muestran en la Tabla 8. La capacidad del eslabón 2 es inferior a la del eslabón 3 debido a que el primero soporta la mayor parte del peso. La trayectoria escogida está dada por la posición más comprometida en cuanto al peso, o sea partiendo de la posición horizontal.

El modelo dinámico del manipulador también puede ser utilizado para diseñar un control de fuerza multi-variable, u otros controladores más avanzados del tipo adaptativo y robusto. Un análisis de este tipo se sale de los objetivos de este trabajo.

 

5.- CONCLUSIONES

 

En este trabajó se obtuvo el modelo cinemático directo e inverso para la posición y velocidad de un manipulador robótico de cuatro grados de libertad. El modelo cinemático se validó de forma práctica utilizando una plataforma de validación experimental y se analizaron los errores cometidos en las pruebas realizadas. Además, se derivó el modelo dinámico del manipulador, el cual se validó utilizando una simulación.  Mediante un algoritmo de programación, y haciendo uso del modelo obtenido, se calculó la capacidad de carga del mismo. El resultado de este trabajo puede ser aplicado a cualquier manipulador robótico con la misma estructura del propuesto. Por otra parte, si se sigue el método aplicado, se podrán encontrar los modelos de otros manipuladores con menos o más grados de libertad. La plataforma construida permite además, realizar otros experimentos, ya sea mecánicos o de control que sean requeridos por investigaciones futuras.

 

REFERENCIAS

 

1.           Siciliano B, Sciavicco L, Villani L, Oriolo G. Robotics Modelling, Planning and Control. Springer; 2009.

2.           McCutcheon R, Pethick R, Bono B, Burak M. The new hire: How a new generation of robots is transforming manufacturing. PwC Manuf Inst. 2014;1-16. Disponible en: https://www.pwc.com/us/en/industrial-products/assets/industrial-robot-trends-in-manufacturing-report.pdf

3.           Verma A, Gor M. Actuator design for arc welding robot. Kathmandu Univ J Sci Eng Technol. 2010;6(2):48-53.

4.           Iqbal J, Khan ZH, Khalid A. Prospects of robotics in food industry. Food Sci Technol. 2017;1-7.

5.           Kostić D, de Jager B, Steinbuch M, Hensen R. Modeling and identification for high-performance robot control: An RRR-robotic arm case study. IEEE Trans Control Syst Technol. 2004;12(6):904-19.

6.           Barrientos A, Peñin LF, Balaguer C, Arcil R. Fundamentos de Robótica. McGraw-Hill; 1997. 28-314 p.

7.           Spong MW, Hutchinson S, Vidyasagar M. Robot dynamics and control. 2nd ed. Vol. 28, Automatica. 2004. 5-303 p.

8.           Fuente JD, Santiago J, Román A, Dumitrache C, Casasanto D. Handbook on Robotics. Siciliano, editor. Vol. 25. Berling: Springer; 2014. 1682-1690 p.

9.           Radavelli LA, Martins D,De Pieri ER , Simoni R. Cinemática posicional de robôs via iteração e quatérnios. En: Proceeding Series of the Brazilian Society of Computational and Applied Mathematics. 2015.

10.         Jazar RN. Theory of Applied Robotics: Kinematics, Dynamics, and Control. 2nd ed. Springer; 2010. 893 p.

11.         Craig JJ. Introduction to Robotics. 3rd ed. Pearson; 2005.

12.         Kardoš J. The Simplified Dynamic Model of a Robot Manipulator. En: Proceedings of the 18th International Conference. 2010. p. 1-6. Disponible en: http://dsp.vscht.cz/konference_matlab/MATLAB10/full_text/055_Kardos.pdf

13.         Spong MW, Hutchinson S. Robot Modeling and Control. 1st ed. Vol. 141. John Wiley & Sons, INC; 2006. 419 p.

14.         Quintero P. Modelo cinemático dinámico del mini robot móvil RICIMAF. Revista Ingeniería Electrónica, Automática y Comunicaciones ,RIELAC. 2012; 33(3):49-62.

15.         Bamdad M, Taheri F, Abtahi N. Dynamic analysis of a hybrid cable-suspended planar manipulator. Robot Autom (ICRA), 2015 IEEE Int Conf. 2015;1621-6.

16.         Chiddarwar SS, Babu NR. Optimal trajectory planning for industrial robot along a specified path with payload constraint using trigonometric splines. Int J Autom Control. 2012;6(1):39-65. Disponible en: http://www.scopus.com/inward/record.url?eid=2-s2.0-84857318993&partnerID=40&md5=3e73e532887b43b2b98bf6125e6f625c.

17.         Milanés Hermosilla D, Castilla Pérez A. Generación de trayectorias para el brazo robótico ( ArmX ). RIELAC. 2016;XXXVII:58-71.

18.         Tanev TK. Singularity Analysis of a Novel Minimally-Invasive-Surgery Hybrid Robot Using Geometric Algebra. En: Wenger P, Chevallereau C, Pisla D, Bleuler H, Rodić A, editores. New Trends in Medical and Service Robots: Human Centered Analysis, Control and Design. Cham: Springer International Publishing; 2016. p. 15-29. Disponible en: http://dx.doi.org/10.1007/978-3-319-30674-2_2.

19.         Montgomery DC. Diseño y Análisis de Experimentos. México: Grupo Editorial Iberoaméricana; 1991.

20.         Bowling A, Khatib O. Dynamic loading criteria in actuator selection for desired dynamic performance. Adv Robot. 2003;17(7):641-56.

 

 

Recibido: 11 de mayo del 2017
Aprobado: 9 de septiembre del 2017

 

 

Eileen Cardoso Espinosa, Ingeniero en Automática, [e-mail]. Principales intereses de investigación: Modelación matemática aplicada a la ingeniería, Robótica industrial, Automatización.