Aplicaciones industriales

Influência da política de testes periódicos na confiabilidade de sistemas tecnológicos

Influencia de la política de pruebas periódicas en la confiabilidad de sistemas tecnológicos

Influence of the periodic tests policy on the reliability of technological systems

José de Jesús Rivero Oliva^{1  *}  , Manuel Perdomo Ojeda² 

¹Escuela Politécnica. Universidade Federal do Rio de Janeiro (UFRJ). Brasil

²Instituto Superior de Tecnologías y Ciencias Aplicadas. Universidad de La Habana (UH). Cuba

RESUMO

O artigo propõe uma metodologia para a construção e avaliação de árvores de falhas de sistemas em espera, com componentes redundantes testados periodicamente, que avalia o impacto das políticas de testes periódicos na indisponibilidade do sistema, através de modelos de indisponibilidade média. A comparação com a análise de indisponibilidade instantânea mostra que o modelo considera adequadamente as políticas de testes periódicos, a partir de dados usualmente registrados nas usinas nucleares. A fórmula para calcular a indisponibilidade média de componentes é generalizada com a inclusão da eficiência e degradação por testes. O modelo foi aplicado à análise de um sistema simplificado, mostrando sua efetividade para avaliar políticas e intervalos de testes, com recomendações para a otimização destes últimos. Sua importância radica na possibilidade de integração ao modelo geral de APS da instalação, em vez de permanecer como uma avaliação separada e complementar.

Palavras-Chave: testes periódicos; árvores de falhas; indisponibilidade média; indisponibilidade instantânea

RESUMEN

El trabajo propone una metodología para la construcción y evaluación de árboles de fallos de sistemas en espera, redundantes, con componentes probados periódicamente, que evalúa la influencia de las políticas de pruebas periódicas sobre la indisponibilidad del sistema, mediante modelos de indisponibilidad media. La comparación con los análisis de indisponibilidad instantánea demuestra que el modelo refleja de forma adecuada las políticas de pruebas periódicas, a partir de datos habitualmente registrados en las centrales nucleares. Se generaliza la fórmula para el cálculo de la indisponibilidad media de componentes con la inclusión de la eficiencia y la degradación por pruebas. El modelo fue aplicado al análisis de un sistema simplificado, mostrando su efectividad para evaluar políticas e intervalos de pruebas, con recomendaciones para la optimización de estos últimos. Su importancia radica en la posibilidad de integración al modelo general de APS, en lugar de permanecer como una evaluación separada y complementaria.

Palabras-clave: pruebas periódicas; árboles de fallos; indisponibilidad media; indisponibilidad instantánea

ABSTRACT

The paper proposes a methodology for the construction and evaluation of fault trees for stand-by redundant systems, periodically tested, evaluating the influence of the periodic tests policy on the system unavailability, through a mean unavailability model. The comparison with the instantaneous unavailability analysis shows that the model adequately reflects the periodic tests policies, based on data usually recorded in nuclear power plants. The formula for calculating the components mean unavailability was generalized with the inclusion of test efficiency and test-caused degradation. The model was applied to the analysis of a simplified system, showing its effectiveness to evaluate policies and test intervals, with recommendations for the optimization of the latter. Its importance lies in the possibility of its integration into the general PSA model of the facility, instead of remaining as a separate and complementary evaluation.

Key words: periodic tests; fault trees; mean unavailability; instantaneous unavailability

Introdução

Na indústria nuclear, a Análise Probabilista de Segurança (APS) é amplamente reconhecida como uma metodologia essencial para a análise de segurança e a tomada de decisões sobre esta importante matéria ^[1- ^3]. Por outra parte, de forma crescente aparecem na literatura diversas aplicações em outras indústrias com altos padrões de confiabilidade e segurança ^[4, ^5].

Uma tarefa importante da APS á a análise de confiabilidade mediante árvores de falhas, de sistemas de segurança que permanecem em espera. Estes sistemas estão compostos por trens redundantes, submetidos a testes periódicos para detectar e corrigir a tempo a progressão de falhas ocultas que impediriam enfrentar com êxito uma demanda real ^[3, ^6]. Infelizmente, os testes periódicos apresentam também efeitos adversos, de modo que testes muito frequentes poderiam conduzir a uma diminuição em lugar de aumento da disponibilidade. Entre estes efeitos negativos se encontram o tempo que o componente permanece total ou parcialmente indisponível durante o teste, assim como o estresse causado pela própria demanda do teste.

Tipicamente, a APS modela os componentes na etapa de vida útil do seu ciclo de vida e assume suas taxas de falha como valores constantes. Este é um dos pontos mais questionados por vários autores, que consideram uma insuficiência a não inclusão do estresse causado pelas demandas e o envelhecimento, como fatores que produzem um aumento da probabilidade de falha (ρ) e a taxa de falha (λ) dos componentes. Também se considera que o uso na APS de um modelo simples de indisponibilidade média para os componentes testados periodicamente, limita a modelação adequada das políticas de teste e manutenção ^[1, ^3]. Como resposta a estes problemas têm sido propostos diversos modelos de confiabilidade de componentes. Vários deles tentam caracterizar a confiabilidade dos componentes testados periodicamente da forma mais realista possível ^[7-^9]. Devido à coexistência de efeitos positivos e adversos, a otimização do intervalo de testes atendendo a critérios de disponibilidade e custos, é um dos tópicos mais tratados ^[3, ¹⁰, ¹¹, ^12].

Alguns modelos estão orientados fundamentalmente ao envelhecimento ^[3, ^9]. Em ^[3], se analisam sistemas simples de dois e três componentes com testes sequenciais e escalonados, determinando as expressões analíticas da probabilidade de falha média conjunta mediante dois modelos de envelhecimento: linear e Weibull. O exemplo de aplicação corresponde ao sistema de injeção de alta pressão (HPIS) de uma usina nuclear de tecnologia Westinghouse, que também aparece nos trabalhos de outros autores. Os dados de taxa de falha e probabilidade de falha de bombas e válvulas são tomados deste exemplo, que provem originalmente do relatório EPRI NP-4317 ^[13]. Por outra parte, as taxas de envelhecimento foram extraídas da base de dados conhecida como TIRGALEX ^[14], que se considera proporciona valores médios genéricos de grande incerteza ^[3].

Em ^[9], se apresenta um modelo de envelhecimento mais detalhado, baseado na indisponibilidade instantânea, e que inclui fatores adicionais como o estresse das demandas reais e testes, assim como certo grau de envelhecimento remanente depois da manutenção. Não obstante, o modelo se aplica a um único componente, uma válvula, usando também os dados provenientes de EPRI NP-4317 e TIRGALEX. São propostas duas estratégias de aumento da disponibilidade, uma delas consistente em inspeções on-line de alguns elementos, que podem ser controlados mediante detectores, sem ser demandados. Para estas inspeções se inclui um fator de eficiência de detecção denominado cobertura de detecção (0 ≤ C_det ≤ 1).

Outros trabalhos detalham mais os efeitos do estresse causado pela demanda. Assim, em ^[7], a análise se concentra no estresse dos testes sobre ρ, mas sem considerar os efeitos sobre λ e tampouco o envelhecimento. Desenvolve-se um modelo de indisponibilidade instantânea que inclui manutenções preventivas imperfeitas, com um fator de redução da taxa de falha (0 ≤ ε ≤ 1) conjuntamente com um fator de eficiência do teste (0 ≤ η ≤ 1) em lugar da cobertura de detecção usada em ^[9]. A aplicação se realiza apenas a uma válvula, usando os dados do relatório EPRI NP-4317 ^[13].

Por sua vez, o modelo desenvolvido em ^[11], determina a indisponibilidade média dos componentes considerando uma manutenção periódica imperfeita com parâmetro de efetividade (ε) e envelhecimento. Este modelo não inclui o aumento de ρ e λ devido ao estresse causado pelos testes. Destina-se a componentes com itens múltiples, dando a possibilidade de estratégias de teste e manutenção distintas para partes diferentes de um único equipamento. Aplica-se ao HPIS de tecnologia Westinghouse já mencionado, considerando por separado a parte elétrica e mecânica das bombas e válvulas.

Alguns artigos estão dedicados especificamente aos sistemas de instrumentação e controle ^[10, ^15]. Neste tipo de sistemas são consideradas taxas de falha com perigo (contribuintes à falha do sistema) e seguras (falsos alarmes que conduzem a acionamentos espúrios). Em ^[10], se apresenta uma metodologia baseada em uma análise de indisponibilidade instantânea para diferentes estratégias de testes. As taxas de falha se dividem em detectáveis e não detectáveis, a partir de um parâmetro de cobertura de detecção. Em ^[15], se generalizam as fórmulas para a determinação da indisponibilidade média, exigidas por norma, para cobrir não só testes completos senão também testes parciais. Desenvolvem-se fórmulas analíticas para os diferentes tipos de redundância previstos na norma, que depois são verificados mediante cadeias de Markov.

Precisamente, outra linha de pesquisa é a análise e otimização de estratégias de testes mediante cadeias de Markov ^[1, ^12]. Em ^[1], se determina a indisponibilidade de um sistema mediante a solução assintótica de um modelo de Markov que considera os testes periódicos, a manutenção corretiva derivada do teste e o tempo permissível fora de serviço (AOT) para três políticas de teste e reparo. Em ^[12], se analisa um sistema de dois componentes redundantes reparáveis, testados periodicamente, mediante uma cadeia de Markov de tempos discretos.

Resulta importante sem dúvidas o desenvolvimento dos novos modelos antes mencionados orientados a descrever a indisponibilidade de componentes testados periodicamente de forma mais detalhada e realista. Não obstante, para conseguir este propósito plenamente é necessário que eles sejam avaliados com dados corretos.

Este tipo de modelo leva a um primeiro problema prático, que é a necessidade de separar quantitativamente as contribuições derivadas do estresse ocasionado pela demanda (ρ) dos modos de falha relacionados com o tempo em espera (λ). Ou seja, é preciso que os sistemas de coleta de dados nas plantas permitam diferenciar se a falha de um componente ante uma demanda aconteceu porque o componente já estava falho ou porque o estresse que lhe produziu a demanda o fez falhar no momento em que foi acionado.

Outro inconveniente, reconhecido por vários autores ^[3, ⁹, ^11], é a dificuldade para a estimação dos dados, fundamentalmente de degradação por testes e envelhecimento. Estes modelos necessitam dados adicionais que não são registrados habitualmente nas plantas. Seria necessário contabilizar por separado taxas de falha e probabilidades de falha, assim como discriminar que frações de um incremento observado nos registros de falhas de um equipamento correspondem a estresse da demanda, estresse do teste sobre a taxa de falha em espera, envelhecimento ou manutenção imperfeita.

Esta dificuldade pode ser observada nas aplicações dos modelos com envelhecimento e degradação por testes dos artigos antes mencionados, que tiveram como objeto o mesmo sistema HPIS de Westinghouse, com dados genéricos provenientes das mesmas fontes, EPRI NP-4317 e TIRGALEX.

Por outra parte, a APS é em verdade uma metodologia de análise de sistemas, que abrange numerosos eventos básicos de sistemas tecnológicos diversos. Por este motivo, seus cálculos têm que se basear em valores médios da probabilidade de falha dos eventos básicos, ou seja, um único valor por cada evento. O modelo não resultaria viável se fosse avaliado mediante análise de indisponibilidade instantânea. Portanto, qualquer melhoria nos modelos de confiabilidade de componentes deve ser introduzida fundamentalmente no cálculo da indisponibilidade média. Consequentemente, o desafio principal é tentar que os modelos de indisponibilidade média de componentes consigam descrever o mais fielmente possível as condições reais, fazendo uso de dados acessíveis a partir da experiência operacional específica das plantas.

Neste contexto, o presente trabalho propõe uma metodologia para a construção e avaliação de árvores de falhas de sistemas em espera, redundantes, com componentes testados periodicamente, que considere adequadamente as políticas de testes periódicos sobre a indisponibilidade do sistema, mediante modelos de indisponibilidade média, usando dados habitualmente registrados nas plantas. É realizada a comparação com análises de indisponibilidade instantânea, para demonstrar que as análises de indisponibilidade média, de uso comum em APS, podem modelar de forma adequada as políticas de testes periódicos, a partir de dados habitualmente registrados nas usinas nucleares. Finalmente, se generaliza a fórmula para o cálculo da indisponibilidade média de componentes, de modo que também sejam consideradas a eficiência e a degradação por testes, se fosse possível estimar estes parâmetros a partir de critérios de especialistas, com suficiente credibilidade.

Materiais e métodos

A expressão clássica, usada em APS para a determinação da indisponibilidade média de um componente sujeito a testes periódicos é ^[3]: veja equação(1).

$Q_{\text{media}}=\rho +\frac{1}{2}\lambda T+ \frac{T_t}{T}{q}_t+\left(\rho +\lambda T\right)\frac{T_r}{T}$ (1)

onde:

Qmedia	é a indisponibilidade média do componente.
ρ	é a probabilidade de falha devido à demanda.
λ	é a taxa de falha em espera.
T	é o intervalo de testes.
Tt	é a duração do teste.
qt	é a probabilidade de não poder responder a uma demanda real durante a realização do teste.
Tr	é o tempo médio de reparo.

Os termos da equação (1), representam as contribuições à indisponibilidade devidas a:

• Primeiro termo: Estresse da demanda.

• Segundo termo: Tempo de espera.

• Terceiro termo: Duração do teste.

• Quarto termo: Reparo posterior ao teste, se o componente foi detectado falho.

Esta expressão está baseada no uso de um modelo probabilístico exponencial para as variáveis aleatórias tempo para falhar e tempo de reparo, de modo que as taxas de falha e reparo são consideradas constantes.

Adicionalmente, o segundo termo da equação (1), é resultado de uma aproximação linear do incremento da probabilidade de falha com o tempo, com constante de proporcionalidade λ. Isto resulta válido para λT ≤ 0,1, condição que se cumpre na imensa maioria dos casos de interesse prático na indústria nuclear.

Na equação (1), o segundo termo considera o efeito positivo dos testes que limita a progressão de falhas ocultas durante o tempo de espera, enquanto os termos terceiro e quarto modelam as contribuições negativas devidas ao tempo que o componente permanece indisponível durante o teste e a manutenção corretiva posterior. Do balanço destes fatores contrapostos se determina o intervalo de testes ótimo teórico (T^opt) que mostra a equação (2):

$T^{opt}=\sqrt{\frac{2\left(T_t{q}_t+\rho T_r\right)}{\lambda }}$ (2)

Infelizmente, o uso indiscriminado da equação (1), para todos os componentes de um sistema em espera testados periodicamente conduz a superestimações da probabilidade de falha do sistema ao somar contribuições ilegais, proibidas por especificações técnicas, de dois trens redundantes sendo testados ou reparados simultaneamente. Adicionalmente, a indisponibilidade durante o teste pode estar sendo considerada várias vezes. Por este motivo resulta necessário que, para os componentes que formam parte de trens redundantes, se separe a contribuição do estresse da demanda e a indisponibilidade devida ao tempo de espera das restantes contribuições por indisponibilidade do teste e manutenção corretiva. Quando os componentes da linha redundante se testam juntos (o que é a prática usual) deve ser considerada a indisponibilidade de todo o trem durante o teste e não a de cada componente por separado.

Em consequência, este trabalho propõe um modelo que divide as contribuições à falha do sistema em duas categorias:

1. Combinações de falhas (ρ + ½ λT) de vários componentes de trens redundantes diferentes.

2. Combinações de falhas (ρ + ½ λT) de um ou vários componentes de trens redundantes diferentes com a indisponibilidade por testes ou manutenção corretiva de um único trem distinto.

Adicionalmente, resulta necessário modelar as políticas de testes, que podem ser classificadas em quatro tipos ^[10]:

1. Testes simultâneos, quando todos os componentes se testam ao mesmo tempo. Esta política não resulta adequada para sistemas de segurança e não será avaliada.

2. Testes sequenciais, quando um trem redundante se testa a continuação do outro.

3. Testes escalonados, quando existe uma diferença de fase entre o teste de cada trem.

4. Testes independentes (aleatórios), quando os testes não seguem um padrão determinado. Esta política não é possível em indústrias com altos padrões de segurança e confiabilidade, de modo que também não será considerada no trabalho.

Para a política de testes sequenciais se assumirá que se um trem é detectado falho durante o teste o próximo trem não é testado até haver concluído o reparo do anterior. Adicionalmente, para que o modelo de indisponibilidade média avalie as probabilidades de falha conjuntas de forma correta se modificam os produtos de termos ½ λT, de modo que a contribuição da falha independente de dois componentes não é mais ¼λ₁λ₂T² senão ⅓λ₁λ₂T². Para três componentes a probabilidade de falha independente conjunta é ¼λ₁λ₂λ₃T^3[3].

Por sua vez, a política de testes escalonados é a mais comum e adequada para sistemas de segurança porque aumenta sua disponibilidade, embora demande uma carga de trabalho maior Neste caso, se considera uma diferença de fase uniforme entre o teste de cada trem igual a T/N, onde N é o número de trens redundantes. Para as análises de indisponibilidade média, os produtos de probabilidades de falha independente conjunta são 5/24λ₁λ₂T² para dois componentes e 1/12λ₁λ₂λ₃T³ para três componentes ^[3]. Não serão consideradas as falhas de causa comum, porque elas são contribuintes dominantes e se fossem incluídas não permitiriam apreciar devidamente o impacto da política de testes sobre as probabilidades de falha independente conjunta de vários equipamentos. Não obstante, é conhecido que o escalonamento dos testes reduz a contribuição das falhas de causa comum (porque diminui o tempo em que os mecanismos de falha em espera se desenvolvem simultaneamente em componentes redundantes) e também a probabilidade de que um erro humano possa deixar indisponíveis vários destes equipamentos.

A proposta do presente trabalho é aplicar a equação (1), como modelo de confiabilidade de componentes nas árvores de falhas de sistemas redundantes em espera, mas separando as contribuições de indisponibilidade por testes e manutenção corretiva da forma indicada, e realizando também pequenos ajustes nos coeficientes numéricos dos termos de falha conjunta independente para diferenciar as políticas de testes sequenciais e escalonados. Os resultados mostram como estes ajustes permitem aproximar o modelo de indisponibilidade média às avaliações mais detalhadas de indisponibilidade instantânea, com a vantagem de que a análise baseada em indisponibilidade média permite identificar com maior facilidade (mediante medidas de importância) a participação relativa de cada evento básico como contribuinte à indisponibilidade ou risco total.

A metodologia utiliza os dados habitualmente coletados nas plantas ou definidos mediante as especificações técnicas, tais como taxas de falha e intervalo e duração dos testes. Portanto, se assumirá ρ = 0 e serão consideradas apenas as taxas de falha λ dos componentes.

Sobre a manutenção corretiva derivada do teste o mais adequado é usar como indisponibilidade média o tempo de indisponibilidade registrado por esta causa na planta dividido pelo tempo total de exposição às falhas. Se esta informação não estiver disponível, pode ser usado o tempo médio de reparo, medido em planta ou estimado por especialistas, conjuntamente com a taxa de falha, que é precisamente como se avalia no quarto termo da expressão (1).

O grau de indisponibilidade durante o teste q_t é outro dado necessário. A maioria dos trabalhos considera q_t = 1, ou seja, que o componente não seria capaz de responder a uma demanda real quando está sendo testado devido a que os procedimentos de isolamento exigidos pelo teste impediriam sua resposta imediata ^[3, ⁷, ⁹, ¹⁰, ^11]. Pelo contrário, ^[8] considera que os testes não causam indisponibilidade (q_t = 0) porque ante uma demanda real sempre existe tempo suficiente para terminar o teste, realinhar o sistema e cumprir a função de segurança. Na verdade, q_t depende da forma em que o teste é realizado e seu valor pode ser estimado para aqueles casos em que o componente permaneça isolado do sistema durante o teste. Quando não existem diferenças entre as condiciones do teste e a demanda real q_t pode ser considerada zero. Neste trabalho se assumirá q_t = 1, por ser a aproximação mais conservadora.

Finalmente, a equação (1), do modelo de indisponibilidade média pode ser ajustada para considerar outros parâmetros como a eficiência do teste (η) e a degradação resultante do número de testes (n). Esta última correção à indisponibilidade se determina mediante um modelo de incremento linear de ρ e λ como função de n, a partir de valores iniciais ρ₀ e λ₀, respectivamente, usando fatores de degradação constantes: p₁ para ρ e p₂ para λ ^[7]: veja as equações (3) e (4)

$\rho \left(n\right)={\rho }_0\left[1+p_{1}n\right]$ (3)

$\lambda \left(n\right)={\lambda }_0\left[1+p_{2}n\right]$ (4)

Considerando a equação aproximada n_t ≈ (T_c/T) - 1 para o número total de testes n_t em um ciclo de trabalho com duração T_c, conjuntamente com a eficiência do teste η, resulta a seguinte expressão generalizada da indisponibilidade média de um componente testado periodicamente: veja equação (5).

$Q_{\text{media}}={\rho }_{0 }\left(1+\frac{n_t{p}_1}{2}\right)+\frac{1}{2}{\lambda }_0\left(1+\frac{n_t{p}_2}{2}\right)\left[\eta T+\left(1-\eta \right)T_c\right]+ \frac{T_t}{T}{q}_t+{\rho }_{0 }\left(1+\frac{n_t{p}_1}{2}\right)\frac{T_r}{T}+\eta {\lambda }_0\left(1+\frac{n_t{p}_2}{2}\right)T_r$ (5)

Para um modelo que não considere separação entre ρ e λ, ou seja, assumindo ρ = 0, é possível obter a partir de equação (5), a expressão generalizada na equação (6), do intervalo de testes ótimo teórico (T^opt) que, a diferença de a equação(2), inclui também a eficiência do teste e o fator de degradação linear por testes p₂.

$T^{opt}=\sqrt{\frac{{\lambda }_0{p}_2{T}_c\left[\left(1-\eta \right)T_c+2\eta T_r\right]+4T_t{q}_t}{{\lambda }_0\eta \left(2-p_2\right)}}$ (6)

È fácil comprovar essa equação (6), se reduz a (2) quando η = 1 e p₂ = 0. É possível também concluir que tanto o aumento de p₂ quanto a diminuição de η conduzem a um maior valor de T^opt.

A eficiência do teste, necessária para avaliar as equações(5) e (6), pode ser estimada por especialistas profundamente conhecedores do sistema a partir de sua experiência e os registros de planta, de modo que poderia ser considerada na tomada de decisões. Pelo contrário, para p₁ e p₂ é necessário usar valores genéricos provenientes da literatura ^[9] porque são parâmetros de difícil estimação para as condições de uma instalação específica.

Resultados

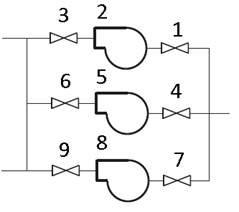
A metodologia se aplica ao sistema HPIS hipotético simples da figura 1, composto por 3 trens redundantes. Todos os cálculos são realizados mediante a aproximação de eventos raros. Os dados de bombas e válvulas aparecem na tabela 1. Eles foram adaptados de ^[3], unindo os valores de ρ e λ em uma única taxa de falha equivalente e assumindo testes de igual duração para todos os componentes de um mesmo trem.

Fig. 1 Sistema HPIS simples. 

Tabela 1 Dados para a análise de confiabilidade do sistema da figura 1. 

Componente	λ [h^-1]	ρ	Tt [h]	T [h]	qt	Tr [h]
Bomba	4,08E-5	0	4,00	2190	1	72
Válvula	7,50E-6	0	4,00	2190	1	8

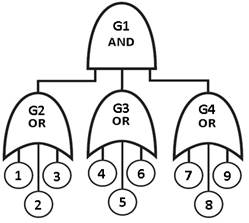
A figura 2, mostra a árvore de falhas (AF), da forma em que tradicionalmente se constrói e avalia como parte da APS.

Fig. 2 AF do sistema da figura 1. 

A avaliação qualitativa determina os 27 cortes mínimos (CM) seguintes:

{1, 4, 7}, {1, 4, 8}, {1, 4, 9}, {1, 5, 7}, {1, 5, 8}, {1, 5, 9}, {1, 6, 7}, {1, 6, 8}, {1, 6, 9},

{2, 4, 7}, {2, 4, 8}, {2, 4, 9}, {2, 5, 7}, {2, 5, 8}, {2, 5, 9}, {2, 6, 7}, {2, 6, 8}, {2, 6, 9},

{3, 4, 7}, {3, 4, 8}, {3, 4, 9}, {3, 5, 7}, {3, 5, 8}, {3, 5, 9}, {3, 6, 7}, {3, 6, 8}, {3, 6, 9}.

Por sua vez, a aplicação da equação (1), ao cálculo da probabilidade de falha média dos componentes conduz a:

q₁= q₃= q₄= q₆= q₇= q₉= 1,01E-2; q₂= q₅= q₈= 4,81E-2

A indisponibilidade média do sistema é obtida avaliando os 27 CM com estas probabilidades. O resultado é uma probabilidade de falha média por demanda de 3,18E-4 . Este é um valor superestimado, insensível à política de testes adotada.

A análise de indisponibilidade instantânea permite comparar as políticas de testes sequenciais e escalonados, estabelecendo valores diferentes para o tempo do primeiro teste de cada trem. Estes tempos aparecem na tabela 2, conjuntamente com os resultados da análise de indisponibilidade instantânea para cada política, realizado mediante a versão EXCEL do software CSolv+ ^[16, ^17].

Tabela 2 Tempo [h] do primeiro teste. 

Indicador	Trem	Política
		Sequencial	Escalonada
Tempo [h] do primeiro teste	1	2182	730
	2	2186	1460
	3	2190	2190
Indisponibilidade do sistema		1,19E-3	2,05E-4

A figura 3, mostra o gráfico de indisponibilidade instantânea para testes sequenciais.

Fig. 3 Indisponibilidade instantânea para testes sequenciais. 

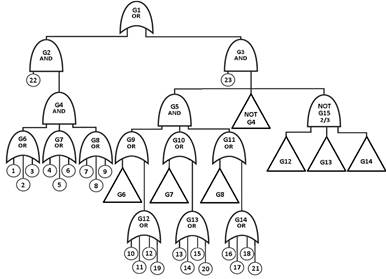
A AF tradicional da figura 2, permite avaliar satisfatoriamente a indisponibilidade instantânea da política de testes escalonados, embora com certa superestimação, devido a que ao avaliar os CM a contribuição da indisponibilidade durante o teste se computa várias vezes (em cada componente do trem) e não como uma indisponibilidade única de todo o trem. É possível apreciar que a indisponibilidade do sistema (2,05E-4) para esta política de uso comum nas usinas nucleares, não está sendo bem considerada pelo modelo tradicional de indisponibilidade media ( 3,18E-4 ). Por outra parte, a indisponibilidade para testes sequenciais (1,19E-3), resulta muito maior, indicando que esta seria a pior política. Não obstante, embora a conclusão seja verdadeira, este resultado está ainda mais superestimado porque, além da consideração da indisponibilidade do teste várias vezes, se computam outras contribuições ilegais de um trem sendo testado enquanto outro ou outros permanecem indisponíveis pelo reparo derivado de um resultado adverso do teste. Para conseguir que o modelo de indisponibilidade média seja sensível às políticas de teste e as considere adequadamente resulta necessário modificar a AF da figura 2, aumentando o número de eventos básicos para separar as contribuições dos testes e a manutenção corretiva. O uso desta nova abordagem detalha mais o modelo sem produzir complicações excessivas. A avaliação pode ser realizada sem dificuldades com um software adequado. A AF detalhada aparece na figura 4, enquanto a tabela 3, mostra os dados de confiabilidade dos eventos básicos que formam parte dela. Nesta tabela os eventos especiais 22 e 23 representam fatores de correção às probabilidades de falha conjunta de dois e três componentes, respectivamente. Estes fatores não são probabilidades. De fato eles são maiores que um quando a política de testes é sequencial. Os valores mostrados na tabela correspondem à política de testes escalonados e são menores que um.

Fig. 4 AF detalhada do sistema da Fig. 1. 

Como resultado da avaliação da AF da figura 4, com os dados de confiabilidade da tabela 3, foram determinados 135 CM e uma indisponibilidade média do sistema igual a 1,85E-4 . Este resultado concorda satisfatoriamente com a indisponibilidade instantânea (2,05E-4), levemente superestimada. Um cálculo de indisponibilidade instantânea, eliminando todo tipo de superestimação, pode ser realizado em um modelo que separe as indisponibilidades dos testes dos componentes e as inclua apenas uma vez como indisponibilidade do trem. Esta avaliação determina uma melhor estimação da indisponibilidade média do sistema, igual a 1,73E-4, de modo que o valor calculado mediante indisponibilidade media é só levemente conservador em comparação com a estimativa realizada mediante indisponibilidade instantânea.

Para avaliar a política de testes sequenciais com o modelo de indisponibilidade média detalhado apenas é necessário repetir o cálculo de indisponibilidade média realizado anteriormente com os valores dos eventos especiais 22 e 23 correspondentes a testes sequenciais. Estes novos valores são 2,0 e 1,33, respectivamente. Desta forma se determina uma indisponibilidade média do sistema com uma política de testes sequenciais igual a 4,95E-4 .

Este valor é 2,68 vezes maior que o correspondente à política de testes escalonados ( 1,85E-4 ), mas não tão alto quanto o obtido mediante indisponibilidade instantânea (1,19E-3), que resulta muito superestimado.

Tabela 3 Dados para a análise de confiabilidade da AF da figura 4. 

Evento básico	Descrição	λ [h^-1]	T[h]	Tt[h]	qt	Tr[h]	Prob. de falha
1	Falha válvula trem 1	7,50E-06	2190				8,17E-03
2	Falha bomba trem 1	4,08E-05	2190				4,34E-02
3	Falha válvula trem 1	7,50E-06	2190				8,17E-03
4	Falha válvula trem 2	7,50E-06	2190				8,17E-03
5	Falha bomba trem 2	4,08E-05	2190				4,34E-02
6	Falha válvula trem 2	7,50E-06	2190				8,17E-03
7	Falha válvula trem 3	7,50E-06	2190				8,17E-03
8	Falha bomba trem 3	4,08E-05	2190				4,34E-02
9	Falha válvula trem 3	7,50E-06	2190				8,17E-03
10	Reparo válvula trem 1	7,50E-06				8	6,00E-05
11	Reparo bomba trem 1	4,08E-05				72	2,93E-03
12	Reparo válvula trem 1	7,50E-06				8	6,00E-05
13	Reparo válvula trem 2	7,50E-06				8	6,00E-05
14	Reparo bomba trem 2	4,08E-05				72	2,93E-03
15	Reparo válvula trem 2	7,50E-06				8	6,00E-05
16	Reparo válvula trem 3	7,50E-06				8	6,00E-05
17	Reparo bomba trem 3	4,08E-05				72	2,93E-03
18	Reparo válvula trem 3	7,50E-06				8	6,00E-05
19	Indisp. trem 1 por teste		2190	4,00	1		1,83E-03
20	Indisp. trem 2 por teste		2190	4,00	1		1,83E-03
21	Indisp. trem 3 por teste		2190	4,00	1		1,83E-03
22	Evento especial 1						6,66E-01
23	Evento especial 2						8,33E-01

Finalmente, se existem os dados necessários, o modelo detalhado de indisponibilidade média pode ser avaliado usando a equação (5), para a confiabilidade de componentes em lugar da equação (1), que serviu de base aos cálculos anteriores. Quando o cálculo é realizado com η = 1 e p₂ > 0, os primeiros dois termos de (5) permitem determinar as probabilidades dos eventos do 1 ao 9 na tabela 3, enquanto os últimos dois termos são usados para os eventos do 10 ao 18. Assim, modificando as taxas de falha da tabela 3, para um total de três testes em um ciclo de trabalho de 8760h, com incremento fracionário de λ em cada teste p₂ = 0,021 ^[9], e realizando novamente o cálculo, é obtida uma indisponibilidade média do sistema para uma política de testes escalonados com degradação, igual a 1,83E-3, 10 vezes maior que o valor base previamente calculado ( 1,85E-4 ).

Quando se considera η< 1 é necessário adicionar nove eventos básicos, do 24 ao 32, para avaliar separadamente as falhas não detectáveis. Aqui o modelo resulta um pouco mais complexo porque os produtos de dois ou três probabilidades de falhas não detectáveis devem ser corrigidos por fatores do tipo testes sequenciais (1,333 ou 2), enquanto os produtos de dois ou três probabilidades de falhas detectáveis continuam sendo multiplicados por fatores de testes escalonados (0,833 ou 0,666).

Por este motivo, neste caso é recomendável estabelecer um valor 1 para os eventos especiais 22 e 23, e incluir manualmente o fator que corresponda, nos CM mais importantes. Realizando o cálculo com valores de η = 0,6, p₂ = 0,021 e T_c = 8760h, tomados de ^[7, ^9], se determina a indisponibilidade média do sistema para uma política de testes escalonados com ineficiência e degradação, igual a 3,90E-3 que, como era de esperar, resulta maior que o valor base previamente calculado ( 1,85E-4 ).

Por sua vez, as equações (2) e (6), permitem estimar o intervalo de testes ótimo para cada tipo de componente, bomba ou válvula. Os resultados dos intervalos de testes ótimos, conjuntamente com os valores correspondentes de indisponibilidade média do sistema, são mostrados na tabela 4.

As bombas, por ter uma taxa de falha maior que as válvulas, fazem uma contribuição também maior à indisponibilidade do sistema. Em consequência, se logram melhores resultados quando se adota um intervalo de testes mais próximo ao valor ótimo das bombas. Como era de esperar, a consideração de efeitos adversos como a ineficiência e a degradação leva a intervalos de testes ótimos maiores. Em todos os casos, os resultados apontam que este sistema aumentaria sua disponibilidade si fosse testado mais frequentemente. A decisão final é sempre uma solução de compromisso que garanta a meta de disponibilidade estabelecida para o sistema e resulte viável desde o ponto de vista de carga de trabalho e custos.

Tabela 4 Intervalos de testes ótimos dos componentes da figura 1. 

Tipo de componente	Intervalo de testes ótimo [h] / Indisponibilidade
	Expressão (2)	Expressão (6) (η = 0,6, p2 = 0,021, Tc = 8760h)
Bomba	443/ 5,81E-6	942/ 2,84E-3
Válvula	1033/ 2,95E-5	1530/ 3,30E-3

O importante é que a análise de confiabilidade seja capaz de avaliar as políticas de teste e seus intervalos com modelos que considerem os processos e contribuições, do modo mais próximo possível ao que realmente acontece na instalação, com dados habitualmente registrados nas plantas ou que possam ser estimados por especialistas, como no caso da eficiência do teste. Também é preciso integrar estes modelos às probabilidades de falha médias usadas nas APS. No que se refere aos fatores de degradação por testes, p₁ e p₂, é possível estudar sua influência mediante modelos teóricos, mas parece mais objetivo considerar os processos de degradação e envelhecimento, atualizando periodicamente o modelo de APS com novos dados e evidencias coletados nas usinas, de modo que a APS seja um modelo vivo, usado sistematicamente na tomada de decisões, conceito que é reconhecido como válido em ^[11].

Conclusões

Foi desenvolvido um modelo de confiabilidade de um sistema redundante em espera, mais detalhado que o tipicamente usado em APS e que evita superestimações importantes, presentes nos modelos atuais. Esta proposta permite eliminar várias contribuições ilegais e, adicionalmente, introduz eventos especiais (fatores de correção) que aproximam a indisponibilidade média aos resultados da análise de indisponibilidade instantânea. O modelo foi aplicado à análise de um sistema HPIS simplificado, mostrando sua efetividade para avaliar políticas e intervalos de testes, com recomendações para a otimização destes últimos. O modelo está baseado em dados habitualmente coletados nas plantas, mas ele também pode considerar outros mais específicos como a eficiência dos testes e o incremento da taxa de falha resultante do estresse do teste. A importância deste modelo radica na sua possibilidade de inclusão como parte do modelo geral de APS de toda a instalação, em lugar de permanecer como uma avaliação separada e complementar.

Referências

Hellmich, M., Berg, H. “Markov analysis of redundant standby safety systems under periodic surveillance testing”. Reliability Engineering and System Safety. 2015, Vol. 133, p. 48-58. Disponível em: http://dx.doi.org/10.1016/j.ress.2014.08.007. ISSN: 0951-8320.

Wang, J., et al. “Fault-tree-based instantaneous risk computing core in nuclear power plant risk monitor”. Annals of Nuclear Energy. 2016. Vol. 95, p. 35 - 41. Disponível em: http://doi.org/10.1016/j.anucene.2016.02.024. ISSN: 0306-4549.

Kancev, D., Cepin, M. “Evaluation of risk and cost using an age-dependent unavailability modeling of test and maintenance for standby components”. Journal of Loss Prevention in the Process Industries. 2011, Vol. 24, p. 146-155. Disponível em: http://dx.doi.org/10.1016/j.jlp.2010.12.003. ISSN: 0950-4230.

Hyun, K. et al. “Risk analysis using fault-tree analysis (FTA) and analytic hierarchy process (AHP) applicable to shield TBM tunnels”. Tunnelling and Underground Space Technology. 2015, Vol. 49, p. 121-129. Disponível em: http://doi.org/10.1016/j.tust.2015.04.007. ISSN: 0886-7798.

Ruiz-Sánchez, T. “PSA applied to the design of non-nuclear plants”. Safety, Reliability and Risk Analysis: Beyond the Horizon. 2014, p. 1925-1934. Editado por Steenbergen, R.D.J.M, et al. Taylor& Francis Group, London. Disponível em: http://doi.org/10.1201/b15938. ISBN: 978-1-138-00123-7.

Berrade, M. D. et al. “Some Insights into the Effect of Maintenance Quality for a Protection System”. IEEE Transactions on Reliability 2015, Vol. 64, No. 2, p. 661-672. Disponível em: http://dx.doi.org/10.1109/TR.2015.2417431. ISSN: 0018-9529.

Martorell, P. et al. “Unavailability model for demand-caused failures of safety components addressing degradation by demand-induced stress, maintenance effectiveness and test efficiency”. Reliability Engineering and System Safety. 2017, Vol. 168, p. 18-27. Disponível em: http://dx.doi.org/10.1016/j.ress.2017.05.044. ISSN: 0951-8320.

Vaurio, J. K. “A recursive framework for time-dependent characteristics of tested and maintained standby units with arbitrary distributions for failures and repairs”. Reliability Engineering and System Safety. 2015, Vol. 138, p. 154-162. Disponível em: http://dx.doi.org/10.1016/j.ress.2015.01.027. ISSN: 0951-8320.

Shin, S. M. et al. “Surveillance test and monitoring strategy for the availability improvement of standby equipment using age-dependent model”. Reliability Engineering and System Safety. 2015, Vol. 135, p. 100-106. Disponível em: http://dx.doi.org/10.1016/j.ress.2014.11.001. ISSN: 0951-8320.

Torres-Echeverría, A. C. et al. “Modelling and optimization of proof testing policies for safety instrumented systems”. Reliability Engineering and System Safety. 2009, Vol. 94, p. 838-854. Disponível em: http://dx.doi.org/10.1016/j.ress.2008.09.006. ISSN: 0951-8320.

Martón, I. et al. “Optimization of test and maintenance of ageing components consisting of multiple items and addressing effectiveness”. Reliability Engineering and System Safety. 2016, Vol. 153, p. 151-158. Disponível em: http://dx.doi.org/10.1016/j.ress.2016.04.015. ISSN: 0951-8320.

Mendes, A., Ribeiro, J.L. “The establishment of the time interval between inspections for a cold standby system with component repair”. Production, 2017, Vol. 27. Disponível em: http://dx.doi.org/10.1590/0103-6513.004917. ISSN: 1980-5411.

Wagner, D.P. et al. Risk-based evaluation of technical specifications. EPRI NP-4317. Palo Alto, California: Electric Power Research Institute, 1985.

Vesely, W.E. et al. Evaluations of Core Melt Frequency Effects Due to Component Aging and Maintenance. NUREG-CR-5510. Washington DC 20555: U.S. Nuclear Regulatory Commission, 1990. Consultado em: 30 de julho de 2018. Disponível em: Disponível em: https://www.nrc.gov/docs/ML0403/ML040350073.pdf .

Innal, F. et al. “PFD_avg generalized formulas for SIS subject to partial and full periodic tests based on multi-phase Markov models”. Reliability Engineering and System Safety. 2016, Vol. 150, p. 160-170. Disponível em: http://dx.doi.org/10.1016/j.ress.2016.01.022. ISSN: 0951-8320.

Rivero, J.J. et al. “Advanced combinatorial method for solving complex fault trees”. Annals of Nuclear Energy. 2018, Vol. 120, p. 661-681. Disponível em: https://doi.org/10.1016/j.anucene.2018.06.019. ISSN: 0306-4549.

Rivero, J.J. et al. “Avaliação de árvores de falhas mediante uma planilha EXCEL”. Revista de Ingeniería Energética. 2018, Vol. 39, No. 1, p. 56-61. Disponível em: http://scielo.sld.cu/pdf/rie/v39n1/rie08118.pdf. ISSN: 1815-5901.

Recebido: 01 de Setembro de 2018; Aceito: 01 de Janeiro de 2019

^*Autor para la correspondencia. E-mail: [e-mail]