ARTICULO ORIGINAL

 

 

Mejoras al método usual de diseño hidráulico de alcantarillas

 

Improvements to the usual method for hydraulic design of sewers

 

 

Profesor-Investigador José Gustavo Morales Nava, Alberto Parra Meza

Facultad de Ingeniería, Arquitectura y Diseño; Universidad Autónoma de Baja California; Ensenada, México.

 

 

---

RESUMEN

Se obtienen fórmulas matemáticas para computarizar el cálculo de la velocidad y el tirante efectivos en el análisis hidráulico de alcantarillas con sección transversal circular para sistemas de drenaje. Se analizan tablas y gráficos de la metodología tradicional que, mediante un tratamiento, derivan en las ecuaciones aquí propuestas. Las fórmulas se obtuvieron usando métodos matemáticos de ajuste de curvas y, para su validación, se compararon resultados procedentes de la metodología usual contra los calculados mediante las ecuaciones propuestas, encontrándolos totalmente confiables. Las ecuaciones logradas son de gran valor al integrarlas en un programa de computación, permitiendo automatizar el diseño sin consultar manuales para establecer el valor de las variables de cálculo con precisión y rapidez.

Palabras clave: análisis hidráulico de alcantarillas, diseño rápido de alcantarillas, fórmulas matemáticas, tirante efectivo, velocidad efectiva.

---

ABSTRACT

Mathematical formulas are obtained to computerize the calculation of effective velocity and depth in the hydraulic analysis of sewers with circular cross section for drainage systems. Tables and graphics of traditional methodology are analyzed, which after some treatment, derive into equations proposed here. The formulas were obtained using mathematical methods of curve fitting and for their validation the results achieved with the usual methodology were compared to those computed by the proposed equations and found to be totally reliable. The equations are of great value when integrated into a computer program, allowing automatic design without handbook consulting to establish accurate values to the variables involved.

Keywords: sewer hydraulic analysis, sewer quick design, mathematical formulas, effective depth, effective velocity.

---

 

 

INTRODUCCIÓN

Desde tiempo inmemorial la humanidad ha padecido epidemias de diversa índole, destacando entre ellas las provocadas por la contaminación al medio ambiente y la falta de higiene en los centros de población. Se debe estar consciente que el hábitat del hombre lo constituyen éste e infinidad de organismos biológicos interactuando y en la medida que se logre una relación armoniosa entre todos, se tendrán mejores oportunidades de convivir en el ecosistema.

Físicamente el entorno está compuesto de aire, tierra y agua los cuales son contaminados en mayor o menor escala por las diversas actividades de la población humana, de allí que los problemas ambientales sean tan antiguos como el hombre mismo y lo nuevo en cuanto a contaminación radica esencialmente en su escala, intensidad y complejidad (Sánchez 2006).

Entre la gran cantidad de problemas que actualmente genera la contaminación del medio ambiente, los que reciben mayor atención en el mundo son los relacionados con la salud pública. Esto obedece a la necesidad de ofrecer a la población en general, el beneficio de mejores condiciones de vida que permitan un mejor desarrollo del ser humano. En México dentro del sector salud, se considera un problema grave la contaminación de los diversos cuerpos de agua (ríos, lagunas, mares, etc.), el aire y la degradación de suelos, porque los desechos generados (sólidos, líquidos y gaseosos) con las diversas actividades de los núcleos poblacionales no reciben el tratamiento adecuado. Lo anterior tiene gran connotación para la salud porque se pueden originar directamente enfermedades entre la población, o constituir un medio apropiado para el desarrollo de elementos nocivos a la salud. Consecuentemente, se deben confinar y eliminar o tratar estos desechos para evitar focos de contaminación, alojamiento y multiplicación de los agentes infecciosos.

Para el tratamiento de los desechos se debe utilizar un procedimiento sanitario que prevenga el contacto de los elementos nocivos con el suelo, agua o aire; entre los diversos métodos usados por el hombre se encuentran los Sistemas de Alcantarillado, que consisten en colectar, transportar, tratar y verter las aguas residuales (agua usada y desechada por la población, actividades comerciales e industriales), así como las aguas producto de lluvias.

La recolección y transporte de aguas residuales y de lluvia en los centros de población, se realiza a través de conductos o tuberías subterráneas de diversos tamaños y materiales a las que se les llama alcantarillas. Para determinar la capacidad de una alcantarilla es necesario efectuar una serie de cálculos que permiten hacer el diseño hidráulico de la misma.

La metodología comúnmente usada para el diseño hidráulico de una alcantarilla, considera el uso de fórmulas tradicionales, así como diagramas y tablas conteniendo valores de algunas características que varían de acuerdo con las condiciones específicas de cada problema. Como la técnica de diseño usada para cada tramo de alcantarilla es repetitiva, en el caso de diseñar la red de un sistema (conformado por gran cantidad de tramos de alcantarillas) el cálculo resulta sumamente tedioso y lento, por lo que se han elaborado varios programas de computación que permiten realizar este diseño en corto tiempo y con eficacia.

Sin embargo, en estos programas no se han podido automatizar adecuadamente todos los cálculos, que son interrumpidos para pedir al usuario que defina el valor (sobre una lista de alternativas que presentan) de algunas variables para ejecutar los cálculos. En este artículo se presentan fórmulas matemáticas que permiten obtener los valores de esas variables sin necesidad de recurrir a gráficos o tablas auxiliares y por tanto, la automatización completa del programa de cálculo para el diseño hidráulico de una alcantarilla.

DISEÑO HIDRÁULICO DE UNA ALCANTARILLA

Algoritmo de diseño

El algoritmo de diseño que presenta García (1991), para usar con programas de computación en sistemas de alcantarillado es el siguiente:

a) Con una fórmula calcular el diámetro necesario de la tubería (alcantarilla).

b) El valor fraccionario calculado, incrementarlo al diámetro comercial inmediato superior.

c) Con el diámetro comercial, calcular mediante fórmula el caudal o gasto a tubo lleno.

d) Con el diámetro comercial, calcular mediante fórmula la velocidad del flujo a tubo lleno.

e) Obtener la relación que existe entre el gasto mínimo (calculado previo a este algoritmo), respecto al gasto a tubo lleno.

f) Obtener la relación que existe entre el gasto máximo (calculado previo a este algoritmo), respecto al gasto a tubo lleno.

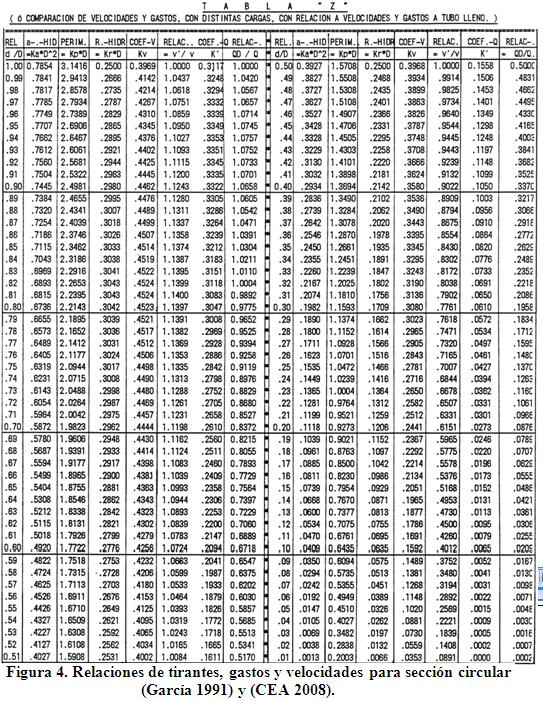
g) Con estas relaciones se ingresa a la tabla «z» (figura 4), donde se obtienen los tirantes mínimo y máximo.

h) De la misma tabla «z» se adquieren las relaciones de velocidad y gasto para tubo parcialmente lleno a tubo lleno y con ellas se calculan las velocidades mínima y máxima verdaderas de acuerdo con las relaciones anteriormente obtenidas.

Como puede observarse, el algoritmo mostrado es usado para cálculos manuales o cualquier programa de computación y en él destaca el uso de una tabla «z», la cual tiene algunas simplificaciones en los pasos del diseño hidráulico, porque no considera el uso de gráficos y otras tablas observadas en publicaciones sobre el tema. Esta tabla «z» que resultó del procesamiento de muchos cálculos, fue presentada por García (1991) y la Comisión Estatal del Agua en Baja California, México (CEA 2008).

Gráficas auxiliares para el diseño tradicional

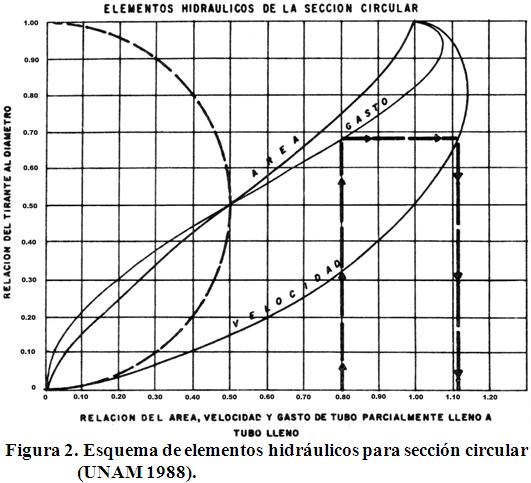
Los esquemas mostrados en las figuras 1 y 2 son y han sido de uso común entre ingenieros para el diseño hidráulico de una alcantarilla y se pueden localizar en cualquiera de los libros o manuales del diseño de sistemas de alcantarillado.

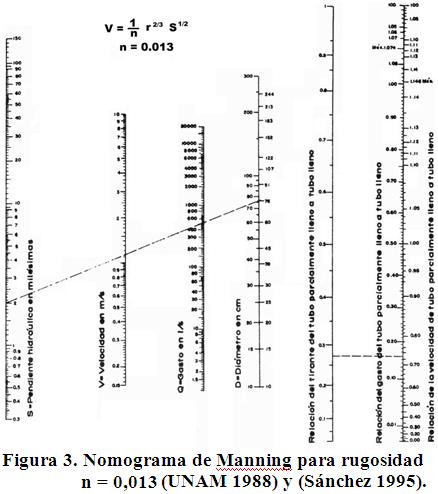
Igualmente el nomograma de la figura 3 y la tabla «z» de la figura 4, son otros elementos de apoyo que aún se continúan usando para el diseño de redes de alcantarillado sanitario y pluvial.

Descripción del cálculo tradicional

De acuerdo con el algoritmo de diseño (García 1991) mostrado en la primera sección, el primer cálculo (inciso a) consiste en determinar el diámetro de alcantarilla necesario para el caudal por conducir y para ello se usa el nomograma de Manning de la figura 3.

Otra forma de determinar el diámetro necesario es usando una fórmula que permita computarizar dicho proceso, la cual se obtiene a partir de la ecuación de Manning para flujo a superficie libre y la ecuación de continuidad, como se indica a continuación.

expresando (1) en términos del diámetro queda:

Substituyendo (2) en la ecuación de continuidad:

Despejando al diámetro de (3) se obtiene la fórmula siguiente:

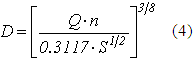
donde:

V es la velocidad del flujo en la alcantarilla (m/s);

n es el coeficiente de rugosidad de Manning (adimensional);

D es el diámetro interior de la alcantarilla (m);

S es la pendiente del tramo de alcantarilla (adimensional);

Q es el caudal que circula por la alcantarilla (m³/s);

R_H es el radio hidráulico de la sección transversal de la alcantarilla (m).

Continuando el cálculo para diseñar la alcantarilla, de acuerdo con el algoritmo de diseño (García 1991), se usan (3) y (2) para obtener respectivamente lo indicado en los incisos c y d. De acuerdo con los incisos e y f del algoritmo de diseño, se determinan las relaciones existentes entre los gastos mínimo (obtenido previo al algoritmo) y a tubo lleno (obtenido mediante (3)), así como la relación entre los gastos máximo y a tubo lleno.

Con estas relaciones de gastos obtenidas y usando cualquiera de las figuras 1-4, se adquieren las relaciones de tirante mínimo respecto al diámetro y tirante máximo respecto al diámetro, obteniendo por consiguiente los valores indicados en el inciso g, correspondientes al tirante mínimo y tirante máximo reales en el flujo de la alcantarilla.

Así mismo, con las relaciones de gastos y las mismas 1-4, se adquieren los valores correspondientes a las relaciones de velocidades entre velocidad mínima y velocidad a tubo lleno obtenida mediante (2), y velocidad máxima entre velocidad a tubo lleno, obteniendo de allí los valores indicados en el inciso h, correspondientes a la velocidad mínima y velocidad máxima reales para el flujo de la alcantarilla.

Finalmente se hacen las comparaciones entre los valores permisibles por reglamentos locales y los obtenidos mediante los incisos últimos g y h, para validar el diseño logrado.

AUTOMATIZACIÓN DEL ALGORITMO

Acorde con el algoritmo de diseño de García (1991) y el método usual, los incisos del a al f son cubiertos mediante el procedimiento y ecuaciones (1)-(4) descritos en la sección anterior y si a eso se añaden las fórmulas definidas en este artículo, se podrán obtener de forma automatizada los valores tratados en los incisos g y h.

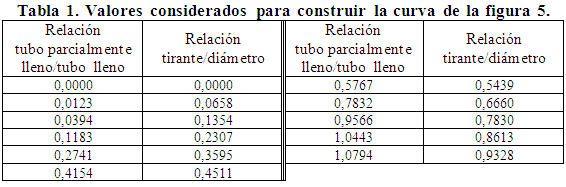
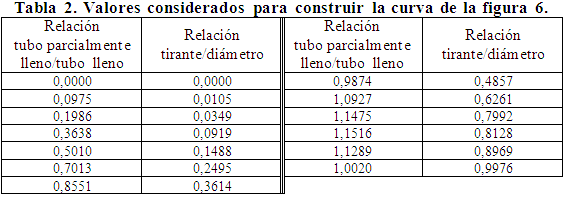
Para ello se parte de las curvas de gastos y velocidades mostradas en las figuras 1 y 2, donde se escogieron determinados puntos característicos y se asignaron pares de valores (coordenados) a cada uno, con los cuales se dibujaron los gráficos de las figuras 5 y 6 conservando la proporción de las curvas originales, cuyos valores se indican en las tablas 1 y 2 respectivamente. Así, la figura 5 presenta la relación de gastos en donde sobre el eje de las abscisas se indicaron los valores de la relación de tubo parcialmente lleno respecto a tubo lleno y en el eje de las ordenadas los valores de la relación de tirante respecto al diámetro. De la misma forma, la figura 6 es una relación de velocidades en donde sobre el eje de las abscisas, se tienen valores de la relación de tubo parcial lleno respecto a tubo lleno y en el eje de las ordenadas la relación de tirante respecto al diámetro. En la figura 5 se anota que la relación de gastos varía de acuerdo con la relación tirante/diámetro, iniciando en un valor igual a cero y llegando hasta un valor de 0,9328 y en la figura 6 de igual forma, la relación de velocidades varía con la relación tirante/diámetro desde cero hasta 0,8128.

Con la curva de la figura 5 y mediante procedimientos matemáticos, se buscó una identidad que diera el mejor ajuste posible para representarla y así se obtuvo una ecuación con coeficiente de correlación igual a 0,99977, cuya expresión es la siguiente:

En donde: t/D es el valor de la relación entre tirante y diámetro (adimensional); RQ es la relación de gastos entre el de tubo parcialmente lleno y el de tubo lleno (adimensional). Esta ecuación tiene validez únicamente para valores de la relación t/D comprendidos entre 0 y 0,9328. El intervalo de valores indicados cubre plenamente los casos prácticos de diseño, acorde con las normas oficiales vigentes en México (leer párrafo aclaratorio en seguida de (6)).

Igualmente con la curva de la figura 6 y mediante procedimientos matemáticos, se buscó el mejor ajuste para representarla y así se obtuvo una ecuación con coeficiente de correlación igual a 0,99986, cuya expresión es la siguiente:

En donde: t/D es el valor de la relación entre tirante y diámetro (adimensional); RV es la relación de velocidades entre la de tubo parcialmente lleno y la de tubo lleno (adimensional). Esta ecuación tiene validez únicamente, para obtener la relación de velocidades de acuerdo con valores comprendidos entre 0 y 0,8128 de la relación de tirante/diámetro. El intervalo de valores indicados cubre totalmente cualquier caso práctico de diseño de acuerdo con las normas oficiales vigentes para sistemas de alcantarillado en México, que permiten en atarjeas, subcolectores y colectores, usarlos parcialmente llenos desde 1/2 hasta 2/3 del diámetro interior (t/D desde 0,5 hasta 0,666); y para interceptores y emisores, usarlos parcialmente llenos desde 2/3 hasta 4/5 del diámetro interior (t/D desde 0,666 hasta 0,80).

Ejercicio de aplicación

A continuación se presenta el diseño de un tramo de alcantarilla sanitaria mediante el método tradicional y mediante un programa de cómputo que utiliza las ecuaciones (5) y (6). Los resultados de ambos métodos son comparados en la tabla 3.

DATOS:

Gasto máximo extraordinario (Q_{máx extr}): 49,97 litros/s

Gasto mínimo (Q_mín): 5,26 litros/s

Pendiente hidráulica (S): 10,2 milésimos

Coeficiente de rugosidad de Manning (n): 0,013

A modo de un ejercicio más de comparación con métodos tradicionales, resulta conveniente mencionar que también existen expresiones exactas que permiten efectuar los cálculos en tuberías parcialmente llenas, como son las indicadas en los libros de Chow (1982) y Gardea (1995), entre otros.

En el libro de Chow (1982), aparece el «CUADRO 2-1. Elementos geométricos de las secciones del canal» donde se muestra en la primera columna denominada Sección, la correspondiente al círculo y en las columnas subsecuentes las fórmulas del Área, Perímetro mojado, Radio hidráulico, etc. Estas fórmulas una vez desarrolladas matemáticamente, permitieron al autor del libro, generar valores en forma de tablas para relacionar cada una de las variables principales (A, P, R, T, D, Z, AR^2/3) de la sección transversal respecto al diámetro del canal circular, lo cual se encuentra en su Apéndice A. Elementos geométricos para secciones de canal circular.

El libro de Gardea (1995), en su sección 2.5 Conductos circulares parcialmente llenos, presenta el croquis de su Figura 2.4 correspondiente a la sección transversal del conducto circular y a continuación unas fórmulas matemáticas con las que es posible calcular el área (A), el perímetro mojado (P) y la longitud del ancho de la superficie libre del líquido contenido en el conducto (B). Estas fórmulas están en función a los valores de las variables que son el radio del conducto circular (r), el tirante del canal (h) y el diámetro del conducto circular (D).

Analizando lo expuesto por Chow (1982) y las fórmulas de Gardea (1995), vienen a ser lo mismo, solamente que las del segundo autor se quedaron en un paso matemático intermedio (por conveniencia del mismo autor) a las expresiones manejadas por el primero de los autores. A continuación se expone el mismo ejercicio de la tabla 3 del presente artículo para comparar resultados y metodología, y en él se usaron las expresiones de Chow (1982).

Ejercicio de aplicación: el mismo indicado anteriormente.

Datos: los señalados con anterioridad.

Diseño:

a) Obtención del diámetro de la alcantarilla:

· De acuerdo con el anteproyecto de la red de alcantarillado, el proyectista está en conocimiento de si el tramo por diseñar corresponde a una atarjea, subcolector, colector, interceptor o emisor y en función a ello, se propone la correspondiente relación tirante/diámetro (y/d₀) a usar en el cálculo inicial.

· Por tratarse del tramo de un colector, del apéndice A se eligió la relación y/d₀=0,66 cuando fluye el gasto en tubo parcialmente lleno y la relación de y/d₀=1,00 cuando fluye a tubo lleno.

· Usando las expresiones del apéndice A no es posible determinar el diámetro necesario para la alcantarilla, porque con los datos del problema, el tirante (y) y el diámetro (d₀) son desconocidos.

b) Fijar diámetro comercial:

Se propone un diámetro comercial suficiente para dar capacidad al gasto máximo. Otra forma de obtener el diámetro que no sea mediante una propuesta, es efectuando los pasos indicados en los incisos a) y b) de la tabla 3, columna Diseño Automatizado, del presente artículo. El diámetro mínimo para una atarjea es de 20 cm y este caso trata el tramo de un colector, por lo que se propuso un diámetro mayor al mínimo, que una vez revisado se comprueba cumpla con la normatividad existente. El diámetro propuesto es d₀ = 0,25 m.

c) Obtener el gasto a tubo lleno:

· Con la relación elegida, del apéndice A se obtiene el valor a usar de la siguiente expresión:

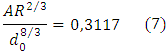
· Cálculo del valor de variables relacionadas con el diámetro propuesto:

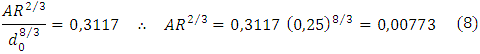
· Usando la fórmula de Manning para canales con flujo uniforme:

Considerando el gasto a tubo lleno (Q_ll) y sustituyendo el valor de la expresión del apéndice A, así como los datos del problema en la fórmula de Manning:

d) Obtener la velocidad a tubo lleno:

· Con la relación elegida, del apéndice A se obtiene el valor a usar de la siguiente expresión:

· Cálculo del valor de la variable relacionada con el diámetro propuesto:

· Usando la fórmula de Manning para canales (1):

Considerando la velocidad a tubo lleno (V_ll) y sustituyendo el valor de la expresión del apéndice A, así como los datos del problema en la fórmula de Manning:

e) No es necesario obtener la relación de gastos indicada para este inciso.

f) No es necesario obtener la relación de gastos indicada para este inciso.

g) Relación de tirantes:

· Para la condición del gasto máximo a tubo parcialmente lleno, se tiene establecida de antemano la relación tirante/diámetro, de donde se obtiene el tirante máximo (y_máx):

· Para la condición del gasto mínimo a tubo parcialmente lleno, se determina el tirante mínimo (y_mín) mediante el siguiente procedimiento:

Usando la fórmula de Manning para canales con flujo uniforme y sustituyendo el gasto mínimo a tubo parcialmente lleno, así como los demás valores de los datos del problema:

Dividiendo el valor anterior entre el diámetro del conducto elevado a la potencia de 8/3:

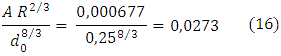
Con el valor obtenido para la expresión anterior, se localiza en el apéndice A (sobre el mismo renglón de la tabla), a qué relación de corresponde y se usa el valor correspondiente:

h) Relación de velocidades:

Para obtener las velocidades verdaderas se utiliza la fórmula de Manning para canales (1), usando los valores de los datos del problema y en el caso del radio hidráulico (R), los valores correspondientes a las dos relaciones tirante/diámetro empleadas en el inciso anterior.

· Velocidad máxima (V_máx):

Para la relación y/d₀ = 0,66, del apéndice A se obtiene R/d₀ = 0,2899

· Velocidad mínima (V_mín):

Para la relación y/d₀ = 0,20, del apéndice A se obtiene R/d₀ = 0,1206

Evaluación de resultados

Los autores aplicaron (5) y (6) a gran cantidad de ejercicios (alrededor de 150), variando diámetros y tirantes que estuvieran dentro de la gama de valores que satisficieran las normas oficiales de México y así validar la cuantía de su uso, observándose una alta precisión en los resultados obtenidos dentro de los intervalos señalados, los cuales fueron comparados contra la solución manual donde se usan los gráficos de las 1-4 y en el cual la precisión del diseño depende de la apreciación visual del proyectista. Ver figuras 7 y 8. Los cálculos, cuando se hacen manualmente (con calculadora) no son tan rápidos con el uso de las ecuaciones (5)-(6), en cuyo caso es preferible usar los gráficos del método tradicional.

En las figuras 7 y 8 que sirven para comparar resultados entre métodos, se observa una curva con línea continua que es representativa para cada una de las ecuaciones (5) y (6) respectivamente (diseño automatizado) y en contraparte a estas curvas, se observan con línea discontinua las obtenidas mediante diseño tradicional.

También podrá apreciarse, que los resultados obtenidos con las expresiones indicadas en Chow (1982), arrojan resultados igual de exactos a los obtenidos con las ecuaciones (5) y (6), pero la gran diferencia entre ellos es que por medio de las ecuaciones se obtienen resultados directamente y con las expresiones (Chow 1982), es necesario hacer la propuesta del diámetro inicial (tanteos), calcular y revisar los valores obtenidos para su cumplimiento con las normas oficiales y de no cumplir se deben hacer nuevos tanteos (iteraciones). Otra opción consiste en usar (4) siguiendo los pasos indicados por los incisos a), b) de la tabla 3, columna Diseño Automatizado y enseguida continuar con las expresiones exactas del apéndice A en Chow (1982).

 

CONCLUSIONES

· Considerando que no existe un tratamiento de la información similar al presente trabajo, las ecuaciones (5) y (6) son de gran valía por su precisión y sencillez de manejo.

· Con ellas es factible la automatización total de estos cálculos para el diseño hidráulico de las alcantarillas.

· Complemento ventajoso resultaría la elaboración de un programa para computadora, que maneje una metodología de cálculo basada en expresiones matemáticas como las aquí mostradas, que resuma la información y permita el procesamiento de datos para el diseño en forma rápida, segura y económica.

 

 

REFERENCIAS

CEA. «Normas técnicas para proyecto de sistemas de alcantarillado sanitario», Comisión Estatal del Agua (CEA), Secretaría de Infraestructura y Desarrollo Urbano, Gobierno del Estado de Baja California, México,2008.

Chow, V. T. «Hidráulica de los Canales Abiertos», Edit. DIANA, México, DF, 1982.

García, J. «Alcantarillado computarizado», Ed. Instituto Tecnológico de Tijuana, Tijuana, Baja California, México,1991.

Gardea, H. «Hidráulica de Canales», Ed. Facultad de Ingeniería, UNAM y Fundación ICA, AC, México, DF, 1995.

Nanni, V. «Técnica moderna del alcantarillado y de las instalaciones depuradoras», Ed. Científico-Médica, Barcelona, España, 1972.

Sánchez, A. «Proyecto de sistemas de alcantarillado», Ed. Talleres Gráficos de la Dirección de Publicaciones, Instituto Politécnico Nacional, México, DF, 1995.

Sánchez, A. «Proyecto de Sistemas de Alcantarillado», Ed. Talleres Gráficos de la Dirección de Publicaciones, Instituto Politécnico Nacional, México, DF, 2006.

UNAM. «Normas de proyecto para obras de alcantarillado sanitario en localidades urbanas de la República Mexicana», Ed. Unidad de Difusión, Facultad de Ingeniería, División de Ingeniería Civil, Topográfica y Geodésica, UNAM, México, DF, 1988.

 

 

Recibido: 10 de enero de 2013.
Aprobado: 15 de enero de 2013.

 

 

José Gustavo Morales Nava, Alberto Parra Meza, Profesor; Facultad de Ingeniería, Arquitectura y Diseño; Universidad Autónoma de Baja California; Ensenada, México, e-mail: [e-mail], [e-mail], e-mail: [e-mail] , [e-mail]