Artículo Original

Determinación de la carga de diseño en los proyectos hidroenergéticos a pie de presa

Determination of the design head in hydropower storage projects

M.A. Luis Gutiérrez Urdaneta¹  , MSc. Leonardo Peña Pupo²  , Ing. Ramón Hidalgo González³ 

¹CUBACONS. San Miguel del Padrón, La Habana. Cuba

²Empresa de Hidroenergía UEB Santiago de Cuba. Santiago de Cuba. Cuba

³Empresa de Hidroenergía. San Miguel del Padrón, La Habana. Cuba

RESUMEN

En Cuba, la carga de diseño preliminar para los proyectos hidroenergéticos “a pie de presa” se determina como el promedio ponderado por el tiempo de las cargas netas obtenidas en la simulación del embalse. En este trabajo se proponen tres métodos alternativos para la determinación de la carga de diseño preliminar óptima en centrales hidroeléctricas “a pie de presa” a saber: 1- mediante la utilización de la carga neta de acuerdo al histograma de frecuencia, 2- a partir de la curva de duración de la carga neta y 3- por el método del gradiente reducido generalizado. Cualquiera de estos tres métodos brinda mayor precisión en la determinación de este parámetro.

Palabras-clave: carga de diseño; curva de duración de la carga neta; optimización de proyectos hidroenergéticos; sitios de baja carga

ABSTRACT

The preliminary design head for run-of reservoir hydropower projects in Cuba is determined as the time-weighted average of net head obtained through reservoir simulation. This paper proposes three alternative methods for obtaining the optimal preliminary design head as follows: 1- by the frequency histogram of the net head, 2- by the net head duration curve and 3- by the generalized reduced gradient method (non-linear programming). Any of these three methods offers a better approximation to this parameter.

Key words: design head; net load duration curve; hydropower project optimization; low load sites

INTRODUCCION

La empresa de hidroenergía (E.H.) está ejecutando un programa de construcción de 34 pequeñas centrales hidroeléctricas, con financiamiento en divisas del Fondo de Kuwait para el Desarrollo Económico Árabe, y se trabaja en el corto plazo la evaluación de otros 38, como parte del Programa de instalación de 56 MW mediante energía hidráulica (^{IHA 2017}). La búsqueda de nuevos sitios es una prioridad estratégica del país y específicamente de la E.H., como contribución al incremento de la generación eléctrica a partir de fuentes renovables de energía.

La optimización de los proyectos de inversión constituye una necesidad vital pues la gran mayoría de los sitios prospectivos en Cuba son de baja carga y potencia. El promedio de carga de diseño (Hd), según estudios de oportunidad y de prefactibilidad, de 38 proyectos a partir de presas es de 14,2 m, y el 87 % de los sitios son de baja carga, según el criterio expuesto en ^{Pérez Franco (1999)} y el resto de carga media. De acuerdo con su potencia, todos son pequeños aprovechamientos hidráulicos (ver figura 1).

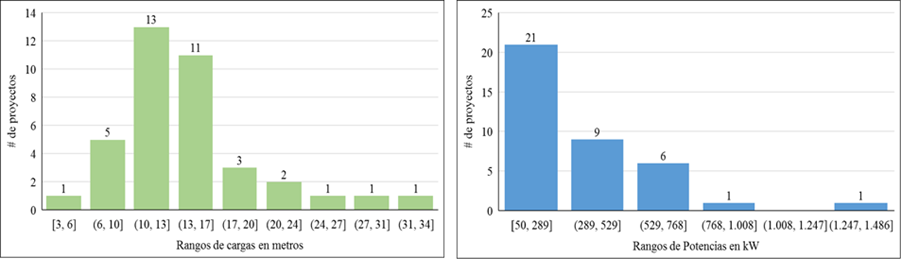
Figura 1 Histogramas de cargas de diseño y potencias preliminares de 38 proyectos a partir de embalses  

Los sitios de baja carga y potencia requieren de la mayor precisión en la determinación de la carga de diseño para lograr que sean económicamente factibles, pues el costo de inversión por kW, de acuerdo con la evidencia internacional, aumenta en la medida que la potencia disminuye (^{ORNL 2012}). Esta regularidad también se observó en el costo del equipamiento de otros proyectos actualmente en ejecución en Cuba (ver figura 2).

Figura 2 €/kW vs. Potencia (dos proveedores de tecnología- Cuba) 

EL ENFOQUE TRADICIONAL

En ^{Pérez Franco (1999)} se define la carga de diseño como la carga … “por encima y por debajo de la cual, el promedio anual de generación por encima y por debajo es aproximadamente igual.” Este enfoque se utiliza también por otros autores (^{AHEC 2008}), (^{Novak et al. 2007}), (^{BR 1976}).

Así, ^{Pérez Franco (1999)} recomienda utilizar como carga de diseño “la media aritmética de las cargas netas disponibles en cada periodo de tiempo” para estudios de pre-factibilidad y factibilidad, aunque precisa que esta carga obtenida puede variar en función de la turbina a utilizar. Bajo esta última recomendación y las propuestas de los autores mencionados (^{AHEC 2008}), (^{Novak et al. 2007}), (^{BR 1976}), la carga de diseño (Hd) se calcularía de la siguiente forma:

$H_d=\frac{{{\displaystyle \sum }}_{\text{1}}^{\text{n}}{\text{Hn}}_{\text{i}}\text{.}\Delta {\text{t}}_{\text{i}}}{{{\displaystyle \sum }}_{\text{1}}^{\text{n}}\Delta {\text{t}}_{\text{i}}}$ (1)

donde:

Δt i	-Periodo de tiempo que dura cada carga neta según dato i
Hn i	-Carga neta según el dato i
n	-número de datos de carga neta - periodo de tiempo

Esta concepción parte del supuesto de que la carga de diseño debe aproximarse a la carga promedio ponderada, pero su selección debe ser tal que las cargas netas máximas y mínimas del embalse no estén fuera del rango permisible de operación de la turbina (^{Pérez Franco 1999}). Este supuesto se muestra explícitamente en la figura 3.

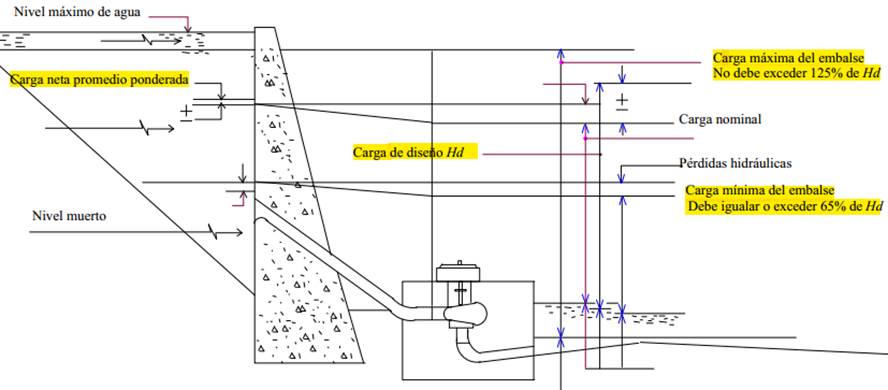[Adaptado de ^{BR (1976)}]

Figura 3 Relación entre las cargas neta máxima y mínima del embalse y los límites operativos de turbinas Kaplan o Francis (Hmáx/Hd= 1,25 y Hmín/Hd= 0,65)  

LAS CARGAS NETAS MÁXIMAS Y MÍNIMAS DE LOS EMBALSES EN CUBA

La mayoría de los embalses analizados muestran cargas máximas y mínimas (mayores que cero), fuera del rango permisible de las turbinas (ver figura 4). Esto se debe a varias razones:

• La mayor parte de los embalses no han sido concebidos para la generación sino para el uso de acueductos y riego.

• La explotación del embalse se realiza con los fines anteriormente señalados y por lo tanto el uso del agua para la generación eléctrica tiene un carácter subordinado a dichos usos.

• El escurrimiento y el gasto está marcados por la estacionalidad en el año y ciclos durante largos periodos de tiempo.

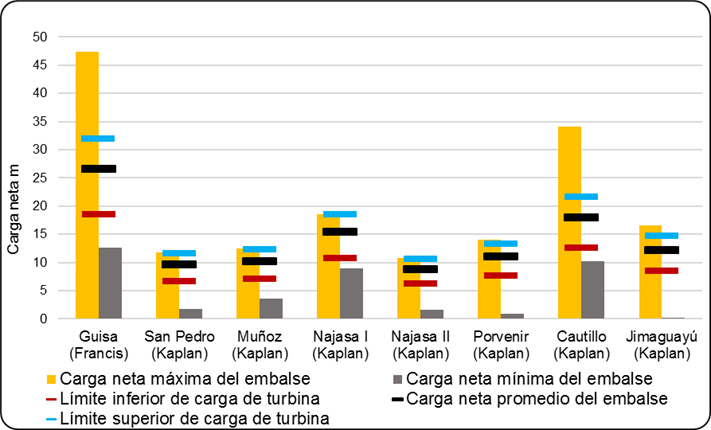
Figura 4 Cargas netas máximas y mínimas en varios embalses / Límites promedio de operación de turbinas de proveedores: Hmáx/Hd= 1,20 y Hmín/Hd= 0,70 

Debido a estas características, el enfoque tradicional para la determinación preliminar de la carga de diseño, según la opinión de los autores, no es el más apropiado para fijar dicho parámetro en la mayoría de los proyectos hidroenergéticos en el país.

Sin embargo, en el ámbito práctico nacional, al menos en las Soluciones Conceptuales ya concluidas para las centrales a “pie de presa”, 13 en total, y ejecutadas por cinco empresas proyectistas cubanas: RAUDAL (Bayamo), Empresa Nacional de Proyectos de la Agricultura (Cienfuegos), Proagua (Pinar del Río), Empresa de Investigaciones y Proyectos Hidráulicos (Camagüey) y Empresa de Investigaciones y Proyectos Hidráulicos (Villa Clara); la estimación de la carga de diseño a partir de carga neta promedio ponderada por el tiempo, según la expresión (1), ha sido la utilizada en todos los casos.

LOS LÍMITES OPERATIVOS DE LAS TURBINAS

Para poder determinar la relación entre las cargas netas máximas y mínimas de los embalses y los rangos operativos de las turbinas se ha realizado una revisión de la literatura nacional e internacional (ver tabla 1).

Los rangos operativos de la carga neta de la turbina Kaplan utilizados en ^{Pérez Franco (1999)}, en los proyectos de las Soluciones Conceptuales elaboradas y en la aplicación informática Simulación Hidroenergética de Embalses CALTUR 11.2012 son más amplios que los del resto de las fuentes consultadas, y mucho más que los índices promedio de los tres proveedores de equipamiento de H.E. (ver tabla 1).

Tabla 1 Límites operativos de carga de turbinas  

Datos a partir de 24 curvas caracterlsticas de turbinas de oferentes en varios proyectos - Límites operativos
Proyecto	Turbina	Proveedor A (Europa)		Turbina	Proveeedor B (Europa)		Turbina	Proveedor C (China)		Promedios de proveedores *
		Hmáx/Hd	Hmín/Hd		Hmáx/Hd	Hmín/Hd		Hmáx/Hd	Hmín/Hd	Hmáx/Hd	Hmín/Hd
Jimaquayú	Kaplan	1,02	0,56				Kaplan	1,16	0,83
Cauto El Paso	Kaplan	1,12	0,67				Kaplan	1,21	0,63
Avilés	Kaplan	1,04	0,62				Kaplan	1,09	0,82
Baraguá	Kaplan	1,14	0,63	Kaplan	1,28	0,84	Kaplan	1,74	0,72
Los Palacios	Kaplan	1,22	0,67				Kaplan	1,18	0,86
Yara	Kaplan	1,15	0,75
Najasa I	Kaplan	1,30	0,78
Cautillo	Kaplan	1,18	0,65				Francis	1,39	0,51
Juventud	Kaplan	1,02	0,61				Francis	1,25	0,65
La Paila	Kaplan	1,14	0,63				Francis	1,14	0,59
Tuinicú	Francis	1,07	0,75				Francis	1,12	0,88
Guaso				Pelton	1,14	0,85
Alacranes							Kaplan	1,30	0,76
							Francis	1,13	0,83
Promedios Kaplan		1,13	0,66		1,28	0,84		1,28	0,77	1,20	0,70
Promedios Francis		1,07	0,75					1,21	0,69	1,20	0,70
Promedios Pelton					1,14	0,85				1,15	0,85

* Los valores promedio Hmáx/Hd fueron redondeados a un múltiplo de 0,05.

Datos de fuentes bibliográficas y proyectos
Tipo de turbina	(Pérez Franco 1999)(Soluciones Conceptuales)		(AHEC 2008) (BR 1976)		(ORNL 2013)
	Hmáx/Hd	Hmín/Hd	Hmáx/Hd	Hmín/Hd	Hmáx/Hd	Hmín/Hd
Kaplan	1,50	0,50	1,25	0,65	1,25	0,50
Francis	1,25	0,65	1,25	0,65	1,25	0,65
Pelton					1,10	0,75
Propela					1,10	0,80

La elección adecuada de los límites operativos de las turbinas, es un elemento fundamental para determinar con mayor precisión la carga de diseño preliminar. Esto será tratado específicamente en un acápite posterior: La importancia de los límites operativos de las turbinas.

MÉTODOS ALTERNATIVOS PARA LA DETERMINACIÓN DE LA CARGA DE DISEÑO PRELIMINAR

Los métodos que a continuación se desarrollan son para una determinación preliminar de la carga de diseño, mediante la maximización de la sumatoria del producto de las cargas netas de la simulación por el tiempo de cada carga, teniendo en cuenta los límites relativos permisibles de las turbinas en relación con la carga de diseño. Siendo el flujo y la eficiencia, constantes y mayores que cero, la generación de energía se optimiza cuando se maximiza Σ Hn _i . Δt _i.

La determinación con mayor rigor de la carga y el flujo de diseño de una instalación hidroeléctrica, si lo que se persigue es maximizar la generación, es un problema complejo y su fijación dependerá de muchas iteraciones de combinaciones de cargas, flujos, número de turbinas, tipo de turbina, potencia, eficiencia y curvas características específicas del equipamiento (^{Pérez Franco 1999}). Si lo que se persigue es maximizar el valor actual neto (VAN), a todos los factores anteriores, deben adicionarse datos de costos de operación, restricciones financieras y funciones e información de costos de inversión (^{Rajšl et al. 2015}), (^{Ilak and Krajcar 2013}).

PRIMER MÉTODO: UTILIZACIÓN DEL HISTOGRAMA DE FRECUENCIA DE LA CARGA NETA

Mediante este método en la simulación del embalse del proyecto Guisa, por ejemplo, se tomaron las cargas netas y el tiempo de cada una. Se procedió de la siguiente forma:

1. Se construyó el histograma de las cargas netas (figura 5) y se obtuvo la tabla 2, resultante del mismo.

2. Se calcularon, con diferentes cargas de diseño, las sumas de las cargas por el tiempo que es capaz de operar la turbina, de acuerdo con los límites operativos de la misma en relación con las cargas de diseño (tabla 3).

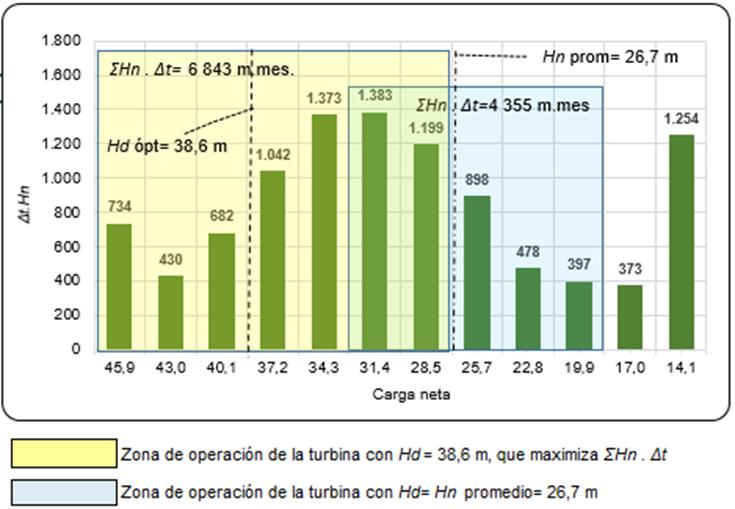
3. Finalmente, para apreciar mejor el aumento de Σ Hn . Δt, con dos variantes, la carga neta promedio y la que maximiza Σ Hn . Δt se construyó un histograma y se señalaron las zonas de operación de las turbinas de acuerdo con diferentes cargas de diseño (figura 6).

Figura 5 Histograma de frecuencias de carga neta - Proyecto Guisa  

Tabla 2 Cálculo del producto de las cargas netas por el tiempo  

Clases Hn (metros)	Hn central de la clase	Δt (meses)	Hn . Δt	% Δt	% Hn . Δt
[47,3-44,4)	45,9	16	734	4%	7%
[44,4-41,6)	43,0	10	430	3%	4%
[41,6-38,7)	40,1	17	682	4%	7%
[38,7-35,8)	37,2	28	1 042	7%	10%
[35,8-32,9)	34,3	40	1 373	10%	13%
[32,9-30,0)	31,4	44	1 383	11%	14%
[30,0-27,1)	28,5	42	1 199	11%	12%
[27,1-24,2)	25,7	35	898	9%	9%
[24,2-21,3)	22,8	21	478	5%	5%
[21,3-18,4)	19,9	20	397	5%	4%
[18,4-15,5)	17,0	22	373	6%	4%
[15,5-12,6]	14,1	89	1 254	23%	12%
TOTALES		384	10 243,0
Hn (promedio ponderado)			26,7

Tabla 3 Cálculo de Σ Hn . Δt para diferentes cargas de diseño 

Hd	Límite máx.	Límite mín.	Σ Δt	Σ Hn . Δt	Comentarios	Abreviatura
24,6	29,5	17,2	118	2 971,9
25,3	30,4	17,7	118	2 971,9
26,0	31,2	18,2	118	2 971,9
26,7	32,0	18,7	162	4 355,0	Hd= Hn promedio	Hn prom
27,4	32,9	19,2	162	4 355,0
28,1	33,7	19,7	162	4 355,0
28,8	34,6	20,2	182	5 330,7
29,5	35,4	20,7	182	5 330,7
30,2	36,2	21,1	182	5 330,7
30,9	37,1	21,6	182	5 330,7
31,6	37,9	22,1	210	6 372,8
32,3	38,8	22,6	210	6 372,8
33,0	39,6	23,1	189	5 894,8
33,7	40,4	23,6	206	6 576,7
34,4	41,3	24,1	206	6 576,7
35,1	42,1	24,6	206	6 576,7
35,8	43,0	25,1	206	6 576,7
36,5	43,8	25,6	216	7 006,7
37,2	44,6	26,0	181	6 108,9
37,9	45,5	26,5	181	6 108,9
38,6	46,3	27,0	197	6 843,2	Hd que maximiza Σ Hn . Δt	Hd ópt
39,3	47,2	27,5	197	6 843,2
40,0	48,0	28,0	197	6 843,2
40,7	48,8	28,5	197	6 843,2
41,4	49,7	29,0	155	5 644,4
Límites de turbinas			Hmáx/Hd	1,20
			Hmín/Hd	1,70

Figura 6 Guisa - Histograma de carga neta vs. Hn.Δt y zonas de operación de turbinas  

De la tabla 3 y la figura 6 se extrajeron las siguientes conclusiones:

• La carga neta promedio no es un buen estimador de la carga de diseño preliminar.

• Aumentando la carga de diseño preliminar de 26,7 m (promedio) a 38,6 m se incrementa Σ Hn _i . Δt _i en un 57 %.

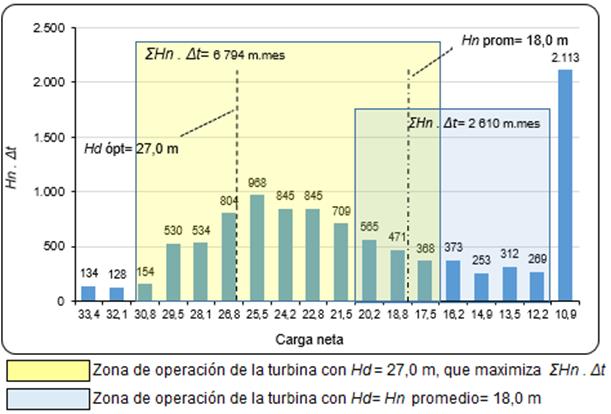
A continuación se muestran otros histogramas de carga neta versus Hn . Δt obtenidos de las simulaciones de los embalses de Jimaguayú y Cautillo, esta vez con los límites operativos de carga neta de las turbinas Kaplan ofrecidas por un proveedor para esos sitios: Hmáx/Hd= 1,27 y Hmín/Hd= 0,70 para Jimaguayú, y Hmáx/Hd= 1,16 y Hmín/Hd= 0,64 para Cautillo (figuras 7 y 8).

Figura 7 Jimaguayú - Histograma de carga neta versus Hn . Δt y zonas de operación de turbinas 

Figura 8 Cautillo - Histograma de carga neta versus Hn . Δt y zonas de operación de turbinas 

Tanto en Jimaguayú como en Cautillo, se obtienen notables aumentos de Σ Hn . Δt cuando se determina la carga que maximiza la utilización de la carga disponible en el tiempo versus la carga neta promedio.

SEGUNDO MÉTODO: EMPLEO DE CURVA DE DURACIÓN DE LA CARGA NETA

La curva de duración de la carga neta, aunque parece no haber sido utilizada en las Soluciones Conceptuales revisadas, ni ha sido hallada en otras referencias prácticas en Cuba, es de uso común internacionalmente en los estudios de factibilidad técnico-económica, como una de las herramientas de análisis (^{AECOM 2011}), (^{ORNL 2013}), (^{Rajšl et al. 2015}).

Por ejemplo, en el software ORNL-Hydropower Energy and Economic Assessment Tool - Version 1.0 (^{ORNL 2013}) se utiliza, como primera aproximación de la carga de diseño, el valor correspondiente al 30 % del tiempo de exceso en la curva de duración de la carga neta.

Esta curva es útil para la evaluación de los sitios de baja y mediana carga y en los que las variaciones de carga neta del embalse tienen impactos significativos en la generación de energía.

Mediante este método, que puede ser más preciso que el anterior, también se toman las cargas netas y el tiempo de cada carga de la simulación del embalse. Se procede de la siguiente forma:

1. Se construye una tabla ordenada (tabla 4) en orden decreciente con las cargas netas y se determina el porcentaje de excedencia de las cargas (como se hace con la curva de caudales clasificados).

2. Se calculan los valores de las áreas debajo de la curva que son utilizadas por la turbina, para diferentes cargas de diseño, de acuerdo a los límites operativos de la turbina. Se determina el área máxima debajo de la curva (tabla 5).

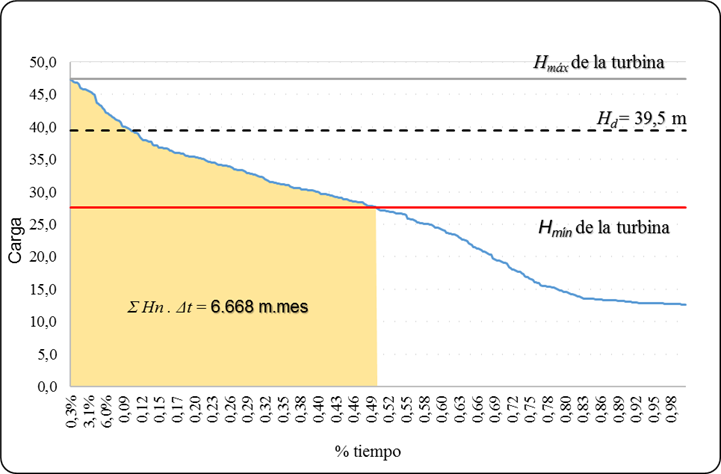
3. Para apreciar mejor los resultados, se construye la curva de duración de la carga, y se determinan las áreas debajo de la curva para la carga neta promedio y para la que maximiza Σ Hn . Δt (figuras 9 y 10).

Tabla 4 Cargas netas ordenadas de forma decreciente y % de excedencia: proyecto Guisa (vista parcial)  

% excedencia	0,3%	0,5%	0,8%	1,0%	1,3%	1,6%	1,8%	2,1%	2,3%	2,6%	…	99,5%	100,0%
Hn (metros)	47,34	47,18	46,98	46,87	46,85	46,55	45,97	45,88	45,76	45,76	…	12,68	12,64

Tabla 5 Cálculo de las áreas debajo de la curva de forma decreciente y % de excedencia 

				Promedio							Máx. área
		Hd	25,50	26,50	28,50	30,50	32,50	34,50	36,50	38,50	39,50	40,50
Hmáx/Hd	1,20	Hmáx	30,60	31,80	34,20	36,60	39,00	41,40	43,80	46,20	47,40	48,60
Hmín/Hd	0,70	Hmín	17,85	18,55	19,95	21,35	22,75	24,15	25,55	26,95	27,65	28,35
		Área	3 514,9	3 967,4	4 802,9	5 692,1	6 205,0	6 483,4	6 570,6	6 603,5	6 667,8	6 444,9

Figura 9 Curva de duración de carga neta: Hd= Carga neta promedio - Guisa (Francis), Hmáx/Hd= 1,2; Hmín/Hd= 0,7 

Figura 10 Curva de duración de carga neta. Hd que maximiza Σ Hn . Δt - Guisa (Francis) Hmáx/Hd= 1,2; Hmín/Hd= 0,7 

TERCER MÉTODO: DETERMINACIÓN DE LA CARGA DE DISEÑO PRELIMINAR MEDIANTE EL GRADIENTE REDUCIDO GENERALIZADO (GRG)

Este es el método más preciso, y utiliza uno de los algoritmos de la programación no lineal. Como en los anteriores de las simulaciones se obtienen las cargas netas resultantes en cada momento.

El planteamiento del problema es el siguiente:

Función objetivo:

$Maximizar {\displaystyle \sum }_{i=1}^{n}H{n}_i . \Delta t_i$ (2)

Restricciones:

$Hd>0;Hd \le máxima H{n}_i$ (3)

$H{n}_i . \Delta t_i=0 \text{si} l_{máx}<H{n}_{i }/H_d <l_{mín}$ (4)

Variable: H _d

Siendo:

Hn i	- carga neta en metros en el mes i
n	- número de meses en la simulación
H d	- carga de diseño
l máx	- límite de operación relativo máximo de carga neta de la turbina
l mín	- límite de operación mínimo relativo de carga neta de la turbina

A continuación, se muestra el cálculo de Σ Hni . Δt _i para la carga neta promedio (tabla 6). Se ejemplificará con los datos de la simulación del embalse Guisa.

Tabla 6 Cálculo de Σ Hn _i . Δt _i para la carga neta promedio (tabla de excel) 

	A	B	C	D	E	F	G	H	I
1	Guisa
2	Hni	Δti	Hni.Δti			ΣHni.Δti	3 967,4	=SUMA(C3:C386)
3	47,34	1	0,00
4	4718	1	0,00			Límites de turbinas	Hmáx/Hd	1,20
5	46,98	1	0,00				Hmín/Hd	0,70
6	46,87	1	0,00
7	46,85	1	0,00			Hn promedio	26,54	=PROMEDIO(A3:A386)
8	46,55	1	0,00
9	46,97	1	0,00
10	45,88	1	0,00
11	45,76	1	0,00
12	45,76	1	0,00
13	45,64	1	0,00
14	45,56	1	0,00

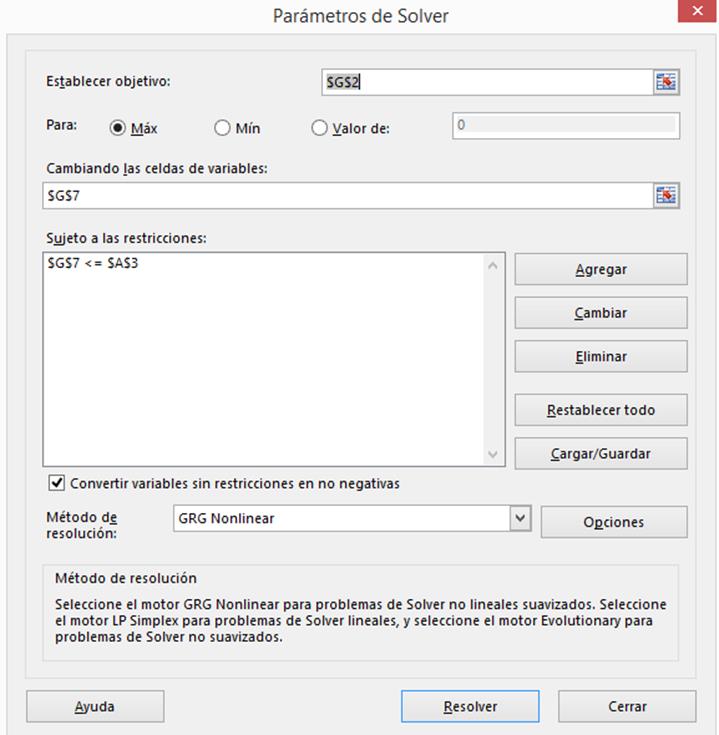
Luego de aplicada la optimización, mediante el motor Generalized Reduced Gradient (GRG nonlinear), se obtiene la carga neta que maximiza Σ Hn _i . Δti (tabla 7 y figura 11).

Tabla 7 Cálculo de la carga neta de diseño que maximiza Σ Hn _i . Δt _i (tabla de Excel) 

	A	B	C	D	E	F	G	H	I
1	Guisa
2	Hni	Δti	Hni.Δti			Maximizar ΣHni.Δti	6 684,2	=Máximo ΣHni.Δti del rango (C3:C386)
3	47,34	1	0,00
4	4718	1	0,00			Límites de turbinas	Hmáx/Hd	1,20
5	46,98	1	0,00				Hmín/Hd	0,70
6	46,87	1	0,00
7	46,85	1	0,00			Hn promedio	38,36	=Hd que maximiza ΣHni.Δti
8	46,55	1	0,00
9	46,97	1	45,97
10	45,88	1	45,88
11	45,76	1	45,76
12	45,76	1	45,76
13	45,64	1	45,64
14	45,56	1	45,56

Figura 11 Aplicación de SOLVER a la tabla 7  

Debe ejecutarse varias veces SOLVER, pues el método GRG obtiene óptimos locales. Se concluye cuando, luego de varias ejecuciones, se determina que se ha llegado al máximo global.

Los resultados de este último método son muy cercanos a los de los dos anteriores, pero la precisión resultante de aplicar el GRG es mayor (tabla 8).

Tabla 8 Comparación del resultado de los tres métodos - proyecto Guisa_. 

	Hd= Hn promedio		Hd= Hn que maximiza Σ Hn. Δt
	Hn promedio	Σ Hn. Δt	Hn óptima	Σ Hn . Δt
Métodos	A	B	C	D	C/A	D/B
1er. Método (histograma)	26,7	4 355	38,6	6 843	1,45	1,57
2do. Método (curva duración carga)	26,5	3 967	39,5	6 668	1,46	1,68
3er. Método (GRG)	26,5	3 967	38,4	6 684	1,45	1,68

En la tabla 9 que sigue se ofrece un resumen general de las características particulares de cada uno de los métodos presentados.

Tabla 9 Comparación de los diferentes métodos 

Criterio	Método tradicional	Métodos que optimizan la producción de energía
		1. Utilización del histograma de frecuencia de carga neta	2. Utilización de la curva de duración de la carga neta	3. Mediante el Gradiente Reducido Generalizado
Fórmula de cálculo	La media aritmética de las cargas netas disponibles en cada periodo de tiempo	La carga de diseño es aquella que maximiza Σ Hn . Δt .
Límites operativos de carga de las turbinas	No se tienen en cuenta.	Los límites operativos de carga de las turbinas ( Hmáx/Hd y Hmín/Hd ) son restricciones en el cálculo de Σ Hn . Δt.
Forma de cálculo	Se obtiene la media aritmética de los datos de la simulación del embalse.	Con los datos de la simulación, y los límites operativos de carga de las turbinas, se construye el histograma de cargas netas. Del mismo se determina la Hd que maximiza Σ Hn . Δt.	Con los datos de la simulación, y los límites operativos de carga de las turbinas se construye la curva de duración de la carga neta. Se determina la Hd que maximiza el área debajo de la curva.	Con los datos de la simulación, y teniendo en cuenta los límites operativos de carga de las turbinas, mediante la el método GRG se obtiene la Hd que maximiza Σ Hn . Δt.
Relación entre Hd y energía a producir	Se determina la Hd estadísticamente. La energía es un valor resultante.	La carga de diseño es aquella que maximiza Σ Hn . Δt, Se realiza un proceso de optimización.
Potencia de diseño	La potencia de diseño dependerá de la carga de diseño obtenida estadísticamente.	Dados el flujo de diseño y la eficiencia general, la potencia de diseño dependerá de la carga neta que optimiza Σ Hn . Δt. Como la carga de diseño obtenida puede ser mayor, igual o menor en magnitud que aquella obtenida por el método tradicional, así lo será la potencia de diseño.
Precisión	Exacto, pues Hd es un valor estadístico.	Como para los cálculos se toman los valores centrales de las clases del histograma, y los intervalos para definir ex ante las posibles cargas de diseño a probar son arbitrarios, Hd y Σ Hn . Δt son valores aproximados.	Como los intervalos para definir ex ante las posibles cargas de diseño a probar son arbitrarios, entonces, Hd y Σ Hn . Δt son valores aproximados.. Es más preciso que el anterior, pues se utilizan directamente las Hni de la simulación del embalse.	Se utilizan directamente las Hni de la simulación del embalse. Con el GRG se obtiene el valor preciso de la Hd que maximiza Σ Hn . Δt. No obstante, debe ejecutarse varias veces para tener la certeza de que ha obtenido un óptimo global.
Aplicación	Cuando las cargas máximas y mínimas del embalse están dentro del rango de carga permisible de las turbinas.	Pueden ser aplicados en todos los casos, incluso cuando cargas máximas y mínimas del embalse están dentro del rango de carga permisible de las turbinas.

LA IMPORTANCIA DE LOS LÍMITES OPERATIVOS DE LAS TURBINAS

Los resultados de estos tres métodos dependerán de los límites operativos de las turbinas utilizados. En última instancia, para una mayor precisión de esta estimación preliminar de la carga de diseño, como antes se ha referido, es necesario contar con las curvas características de las turbinas de los fabricantes.

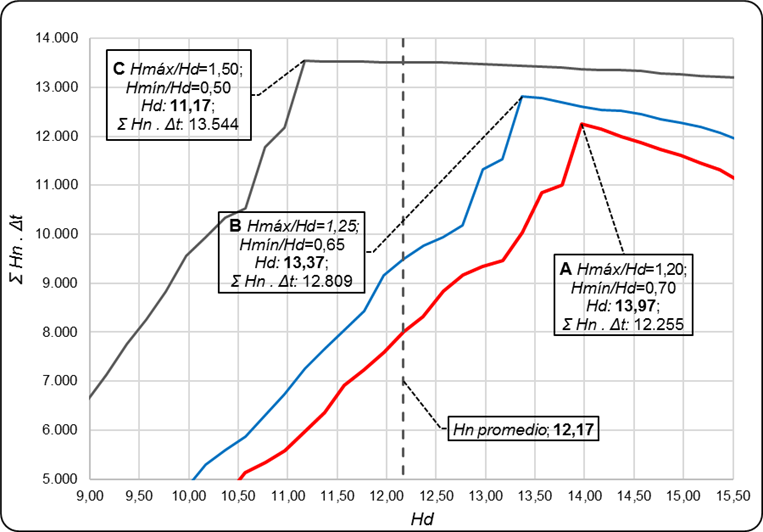
El proceso de cálculo, a partir de las curvas de los proveedores, puede llevar a cambios en la carga de diseño, en dependencia del equipamiento ofertado, y pueden evaluarse varias alternativas de forma sucesiva. Como se observa en la figura 12, con distintos límites operativos de obtienen resultados diferentes.

Figura 12 Cargas de diseño preliminares para diferentes rangos operativos de turbinas Kaplan - Jimaguayú 

CONCLUSIONES

Como se ha probado con este trabajo:

• el promedio ponderado de las cargas netas no es un buen estimador de la carga de diseño preliminar por las características de muchos de los embalses cubanos,

• la carga de diseño determinada de manera preliminar por los tres métodos alternativos descritos aumenta el resultado Σ Hn _i . Δt _i , en relación con el que se obtendría a partir de la carga neta promedio en los ejemplos analizados,

• los métodos aquí propuestos por los autores, de ser utilizados por los proyectistas, coadyuvarán a un cálculo más preciso de este importante parámetro.

Su determinación con mayor rigor es un ejercicio más complejo, y debe realizarse de conjunto con el flujo a través de un proceso iterativo. Este asunto será abordado por los autores en futuros trabajos. Lo que se intenta aquí, con los tres métodos descritos, para la optimización de la carga de diseño preliminar, es proponer herramientas adicionales en el diseño de las instalaciones hidroenergéticas y lograr un acercamiento más fiel al cálculo de ese parámetro de manera inicial.

REFERENCIAS

AECOM (2011). “Don Sahong hydropower project - engineering status report”. AECOM New Zealand Limited, Report 0018 RPPG_E, Internal report, p. IV-V, Auckland, New Zealand.

AHEC (2008). “Guide for selection of turbine and governing system for small hydropower”, Standards/ Manuals/ Guidelines for Small Hydro Developments, Alternate Hydro Energy Centre & Indian Institute of Technology. Internal Report. Ministry of New and Renewable Energy, Govt. of India, India.

BR (1976). “Selecting Hydraulic Reaction Turbines”. Bureau of Reclamation. p. 6-7, US. Government Printing Office, Engineering Monograph No. 20 (limited edition), Washington, USA.

IHA (2017). "Hydropower Status Report. 2017". International Hydropower Association. Editor: R. Taylor: 84 p. HA Annual Report. 2017. IHA Central Office. London. United Kingdom, extraído de: United Kingdom, extraído de: https://www.hydropower.org/2017-hydropower-status-report en enero de 2018.

Ilak P. and Krajcar S. (2013). “Assessment of Investment in Small Hydropower Plants”. Energy and Environment Research, Vol. 3, No. 2, pp. 37, ISSN 1927-0569, Canadian Center of Science and Education, Canadá, 2013.

Novak P., Moffat I. B., Nalluri C. and Rarayanan N. (2007). “Hydraulic Structures”. p. 507, Taylor & Francis, ISBN 0-203-96463-2, Reino Unido.

ORNL (2013). “Technical and economic feasibility assessment of small hydropower development in the Deschutes river basin”. Oak Ridge National Laboratory; p. A14-A39, US Department of Energy, ORNL/TM-2013/221, Internal report, USA.

ORNL (2012). “Small hydropower cost reference model”, Oak Ridge National Laboratory, US Department of Energy, ORNL/TM-2012/501, Internal report, USA.

Pérez Franco D. (1999). “Máquinas hidraúlicas rotodinámicas”. Centro de Investigaciones Hidráulicas, Instituto Superior Politécnico José Antonio Echevarría (Cujae), La Habana, Cuba.

Rajšl I., Krajcar S. and Ilak P. (2015). “Risk-averse approach for assessment of investment in a run-of-the-river power plants while considering reduced water availability”, Journal of Energy, Vol. 64, pp. 153, Faculty of Electrical Engineering and Computing, ISSN 1849-0751 (On-line), ISSN 0013-7448 (Print). University of Zagreb, Special Issue, Croacia, 2015.

Recibido: 21 de Febrero de 2019; Aprobado: 22 de Mayo de 2019

M.A. Luis Gutiérrez Urdaneta. CUBACONS. San Miguel del Padrón, La Habana. Cuba. email: [e-mail]

MSc. Leonardo Peña Pupo. Empresa de Hidroenergía UEB Santiago de Cuba. Santiago de Cuba. Cuba. email: [e-mail]

Ing. Ramón Hidalgo González. Empresa de Hidroenergía. San Miguel del Padrón, La Habana. Cuba. email: [e-mail]