INTRODUCCIÓN
El término genérico ciclón tropical (CT) se emplea para designar a los sistemas de baja presión que se forman en los océanos, en un ambiente homogéneo y generalmente en la zona tropical. El CT como sistema, está acompañado de una amplia área de nublados, precipitaciones, tormentas eléctricas y tiene asociada una circulación superficial de los vientos en sentido antihorario en el hemisferio norte, al contrario de lo que sucede en el hemisferio sur. Los CTs se clasifican de acuerdo con la velocidad que alcanzan los vientos máximos sostenidos (promediados en un minuto) de la siguiente manera: a) depresión tropical (DT): vientos máximos sostenidos inferiores a 63 km/h; b) tormenta tropical (TT): vientos máximos sostenidos entre 63 y 117 km/h y c) huracán (H): vientos máximos sostenidos superiores a 117 km/h (INSMET 2019).
Dentro de los elementos peligrosos asociados con CTs se encuentran las precipitaciones torrenciales. El análisis del comportamiento de las precipitaciones de estos sistemas sobre una cuenca es motivo de interés meteorológico, edafológico, hidrológico e hidráulico, pues proporciona indicadores que permiten realizar estudios de crecidas o la elaboración de modelos de precipitación - escorrentía para un adecuado diseño y dimensionamiento de las obras ingenieriles (Gutiérrez et al. 2017).
Los CTs son sistemas productores de lluvia y las cuencas se benefician con los volúmenes que dichos sistemas aportan. Las precipitaciones producidas por los CTs rebasan los 100 mm y comúnmente los acumulados máximos en menos de 24 horas superan los 300 mm o más; adicionalmente la distribución espacial de las precipitaciones de este origen abarca una amplia zona que, en sentido general, comprende el radio de alcance del sistema, siendo válido destacar que la precipitación asociada a CTs no depende de la intensidad de dichos sistemas. No obstante, con independencia de la categoría del organismo ciclónico, el desplazamiento lento o errático sobre una misma región, o bien de topografía accidentada y la interacción con otros sistemas meteorológicos, puede ocasionar precipitaciones intensas, así como producir inundaciones grandes y destructoras (INSMET 2019).
Perdigón et al. (2019) destacan que el comportamiento de la precipitación ciclónica juega en el tiempo un papel determinante en la forma, magnitud y volumen de las crecidas asociadas en las cuencas afectadas por estos sistemas, lo cual es importante para el diseño de obras de protección tales como sistemas de drenaje, embalses de regulación, estudios de erosión y socavación, etc. Planos (1991), Rodríguez y Marrero (2010), así como Perdigón et al. (2019), de forma general, señalan que el estudio de la variabilidad temporal de la precipitación en Cuba se dificulta por la baja densidad de la red pluviográfica en comparación con la red pluviométrica. En sus contribuciones, proponen metodologías para distribuir temporalmente acumulados de precipitación para una duración prestablecida (ej. 24 horas).
Planos (1991) estudió 100 diagramas de masa pertenecientes a CTs, confirmando la regularidad en la relación lámina-duración y demostrando que durante las primeras 10 - 15 horas de actividad pluvial no se producen incrementos importantes en la lámina de lluvia, pero, transcurrido este intervalo, se intensifica la lluvia, ocurriendo períodos de 4 a 8 horas en los que se acumula más del 50% de la lámina total. El análisis de los diagramas de masa de las precipitaciones de origen ciclónico permitió a dicho autor establecer tres curvas típicas dependientes de la magnitud de la lámina máxima de precipitación: a) inferior a 200 mm, b) entre 200 y 300 mm, c) superior a 300 mm. Esta contribución representa un importante precedente para la prevención hidrológica, particularmente en lo relacionado con el tiempo que ha de transcurrir entre el inicio de la lluvia y su momento más intenso.
Rodríguez y Marrero (2010), también Perdigón et al. (2019)proponen el empleo de los patrones de comportamiento de la lluvia determinado por el Soil Conservation Service (SCS) de los Estados Unidos, y la otra, basada en el estudio de Planos et al. (2011) sobre las intensidades de lluvia mayores de 50 mm para Cuba. Perdigón et al. (2019) procesaron las salidas de precipitación del modelo atmosférico WRF (Weather Research and Forecasting System), y aplicaron un procedimiento para determinar los patrones normalizados de las curvas de masa y los hietogramas respectivos, distribuidos geográficamente en Cuba. Aunque este último proceder parece reflejar adecuadamente los aspectos que influyen en las precipitaciones de CTs a su paso por cada una de las regiones del archipiélago cubano, en ocasiones pueden producirse subestimaciones importantes en las precipitaciones, originadas por las propias parametrizaciones establecidas en el WRF, así como los datos de inicialización para la estimación de variables atmosféricas, por lo que de acuerdo con Planos et al. (2011) y reafirmando lo expuesto por Perdigón et al. (2019), falta avanzar más en el desarrollo de aplicaciones que contribuyan a fortalecer el pronóstico hidrometeorológico en Cuba.
En razón de lo anterior, Planos et al. (2011) aportaron patrones conductuales de las precipitaciones para diversos sistemas, entre los que se encuentran los sistemas meteorológicos tropicales ciclónicos. Dichos patrones son representados por curvas que relacionan la intensidad I, duración y frecuencia (curvas IDF) de los CTs. Como fue expuesto, al ser sistemas productores de lluvias torrenciales, la caracterización de las precipitaciones mediante las curvas IDF permitirán que se faciliten diseños ingenieriles confiables en una herramienta de análisis y planificación en el corto, mediano y largo plazo. No obstante esta importante contribución, en ella no se reportan ecuaciones empíricas, las cuales de acuerdo con Chow et al. (1994) y Minh et al. (2006) presentan cuatro formas básicas usadas (ver tabla 1) para describir la relación entre la intensidad de la lluvia y su duración t:
Estos grupos de ecuaciones empíricas muestran cómo la intensidad de la precipitación decrece con la duración del evento lluvioso asociado con cierta probabilidad de ocurrencia. Además, han sido ampliamente introducidas en aplicaciones prácticas de la hidrología en sentido general.
Tabla 1 Ecuaciones empíricas para curvas IDF
| Autor | Formulación |
|---|---|
| Talbot |
|
| Bernard |
|
| Sherman |
|
| Wenzel |
|
| a, b y n = parámetros de ajuste relacionados a los datos | |
Los estudios realizados por Ballester et al. (1996), citados por Planos et al. (2011), sobre la climatología de los ciclones tropicales que han afectado las distintas regiones del archipiélago cubano permitieron establecer los periodos de retorno en la afectación de estos sistemas a las diferentes regiones del país (ver tabla 2).
Tabla 2 Períodos de retorno (Tr) de los ciclones tropicales sobre las regiones de Cuba
| Región | Intensificación | CT (TT+H) | |
|---|---|---|---|
| TT | H | ||
| Occidental | 2,4 | 2,6 | 1,3 |
| Central | 5,6 | 6,3 | 3,0 |
| Oriental | 4,5 | 4,8 | 2,3 |
[fuente: Planos et al. (2011)]
Al considerar todas las afectaciones de tormentas tropicales (TTs) y huracanes (Hs) clasificadas como CTs (véase tabla 2), nótese la reducción de los periodos de retorno, como consecuencia del aumento de la frecuencia de estos sistemas en la temporada activa que los caracteriza en Cuba. La región Occidental es la más afectada, en cualquiera de las clasificaciones por tipo de sistema (TT, H o CT) según la tabla 2. En un trabajo más reciente, Roura et al. (2018) al realizar la caracterización estadística climatológica de CTs en Cuba durante el periodo 1791-2016, mediante el ajuste de un modelo de Poisson, establecen los periodos de retorno a partir del número de huracanes por año que han afectado al país. En este caso, el periodo de retorno asociado con un solo sistema es T r = 2,41 años.
Planos et al. (2011) en un reporte de investigación relacionado con las grandes precipitaciones y las precipitaciones intensas en Cuba en el periodo 1961-1990, definen los Sistemas Tropicales Ciclónicos (STC) como eventos de elevada capacidad pluvial, donde la lámina de lluvia de 24 horas puede rebasar, fácilmente, los 400 mm. Las precipitaciones que producen estos sistemas tienen un patrón de distribución regular, que depende de la trayectoria de la tormenta y de la relación que se establece entre las características meteorológicas de estos sistemas y los factores zonales de las áreas afectadas. Son muy intensas, principalmente en intervalos de tiempo mayores de 60 min. Por esta razón, aunque la definición de CT está fundamentalmente asociada con la velocidad máxima sostenida de los vientos y los STC están definidos a partir de acumulados de precipitación en 24 horas, en términos generales, los autores emplearán indistintamente ambas clasificaciones. Durante los 30 años estudiados por dicho autor, se identifica que disminuyeron las grandes precipitaciones debidas a los STC, tanto en el número de registros como en la cantidad de situaciones ciclónicas con lluvias que igualaron o superaron 100 mm en 24 horas; siendo relevante la progresiva y acentuada tendencia a la disminución.
En las precipitaciones de origen ciclónico, Planos et al. (2011) plantean que existe un patrón identificable en las relaciones temporales y espaciales, lo que permitió a dichos autores determinar relaciones tipo en localidades homogéneas desde el punto de vista del comportamiento de la precipitación. Dentro de éstas se presentan relaciones tipo que son de extendido uso práctico, teniendo especial relevancia las curvas IDF, así como el coeficiente de avance de la tormenta r. Las curvas IDF para los STC se obtienen a partir de las características de las precipitaciones según su origen y probabilidad de ocurrencia (ver tabla 3, prob = 1/T r ). El conocimiento de las precipitaciones asociadas con este tipo de sistema hidrometeorológico puede establecer criterios de diseño para obras de ingeniería de diverso tipo.
En la presente contribución será utilizada la formulación de Wenzel (ecuación 1.d), aunque es válido destacar que la de Sherman (ecuación 1.c) ha sido aplicada por González (1999), citado por Cruz (2001), para obtener las curvas IDF en varias localidades en diferentes provincias de Cuba, para la determinación de hietogramas instantáneos asociados con tormentas, pero a criterio de los autores son prácticamente equivalentes.
Aplicando un método robusto de ajuste, con los datos de la tabla 3, previamente normalizados, será obtenido el vector de los parámetros [a, b, n] T para cada probabilidad de ocurrencia. Es válido destacar que los periodos de retorno reportados por Ballester et al. (1996) y Roura et al. (2018) involucran probabilidades de ocurrencia que se encuentran fuera del rango reportado por Planos et al. (2011), por lo que como única alternativa será necesario introducir una extrapolación en la estimación de los parámetros asociados con las probabilidades reportadas por dichos investigadores. Este procedimiento puede ser polémico, por la incertidumbre implícita en la extrapolación, de manera que debe hacerse cuidadosamente para no incurrir en errores adicionales, incluyendo como parte del análisis la demostración de que los valores estimados son físicamente posibles en la localidad donde se haga el estudio. Esta alternativa ofrece un recurso válido que llena un vacío en el tratamiento probabilístico de valores extremos hidrometeorológicos.
Tabla 3 Curvas IDF de sistemas tropicales ciclónicos para Cuba
| Probabilidad | Duraciones (min) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 5 | 10 | 20 | 40 | 60 | 90 | 300 | 720 | 1440 | |
| 5,7 | 4,8 | 4,1 | 3,3 | 2,7 | 2,2 | 1,5 | 0,9 | 0,5 | |
| 4,2 | 3,6 | 3,0 | 2,4 | 1,9 | 1,6 | 1,0 | 0,6 | 0,3 | |
| 3,0 | 2,6 | 2,2 | 1,7 | 1,4 | 1,1 | 0,7 | 0,4 | 0,2 | |
| 2,2 | 1,9 | 1,6 | 1,2 | 0,9 | 0,8 | 0,4 | 0,3 | 0,2 | |
| 1,4 | 1,3 | 1,1 | 0,8 | 0,6 | 0,5 | 0,2 | 0,1 | 0,1 | |
Las intensidades están en mm/min [fuente: Planos et al. (2011)]
OBTENCIÓN DE LOS PARÁMETROS DE LAS CURVAS IDF ADIMENSIONALES
La utilización de curvas adimensionales es un recurso técnico de excelencia para hacer comparables los registros en localidades físico-geográficamente homogéneas; para dar mayor certidumbre a otras técnicas como la transposición de valores y para tratar los valores anómalos. Para hacer esto, primeramente, se normalizan los tiempos e intensidades de la tabla 3. En este caso, la duración trabajada es T
d
= 1440 min y la intensidad media para cada probabilidad de ocurrencia puede expresarse como
Tabla 4 Curvas IDF adimensionales de STC para Cuba
|
|
|
||||
|---|---|---|---|---|---|
| 0,00347 | 10,99236 | 11,25837 | 12,36860 | 14,23673 | 19,80516 |
| 0,00694 | 9,03609 | 9,59643 | 10,60751 | 12,27755 | 17,32951 |
| 0,01388 | 7,66671 | 8,13551 | 8,94881 | 10,35102 | 14,51002 |
| 0,02777 | 6,12032 | 6,41325 | 6,92150 | 7,80408 | 10,38395 |
| 0,04166 | 4,98072 | 5,19136 | 5,56314 | 6,19319 | 8,06877 |
| 0,06250 | 4,09264 | 4,24423 | 4,50512 | 4,95600 | 6,29608 |
| 0,20833 | 2,74685 | 2,76724 | 2,80137 | 2,86258 | 3,03954 |
| 0,50000 | 1,62970 | 1,63477 | 1,64278 | 1,65804 | 1,70200 |
| 1 | 1 | 1 | 1 | 1 | 1 |
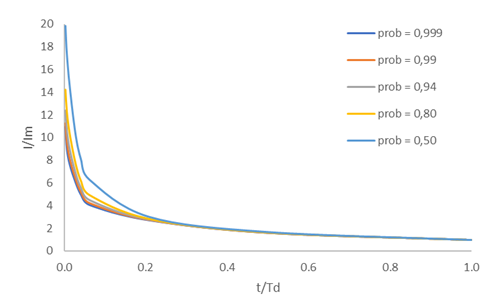
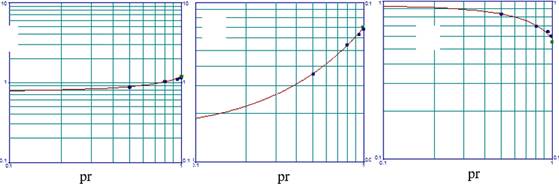
Figura 1 Tendencia de curvas IDF adimensionales obtenidas partir de Planos et al. (2011) para sistemas tropicales ciclónicos
En la tabla 5 se muestran los resultados obtenidos del proceso de estimación de parámetros para la curva IDF de Wenzel de forma adimensional:
Para minimizar la suma de los errores cuadráticos se ha empleado el método de Levenberg-Marquardt, el cual permite arribar a la solución de un sistema de ecuaciones no lineales (Gill et al. 1981).
Tabla 5 Parámetros de las curvas IDF para STC
|
|
Máximo error absoluto | ||||
|---|---|---|---|---|---|
| 0,999 | 1,20780 | 0,06806 | 0,55798 | 0,99748 | 0,25555 |
| 0,990 | 1,15317 | 0,07049 | 0,60813 | 0,99814 | 0,29731 |
| 0,940 | 1,10762 | 0,06347 | 0,64517 | 0,99814 | 0,29731 |
| 0,800 | 1,04422 | 0,05422 | 0,70101 | 0,99817 | 0,33367 |
| 0,500 | 0,88850 | 0,03577 | 0,83519 | 0,99827 | 0,59907 |
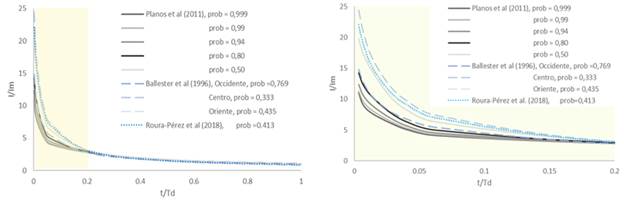
La variabilidad de los parámetros a, b y n con la probabilidad de ocurrencia de los STC, lógicamente también puede ser expresada a través de ecuaciones de ajuste. En este sentido, se ha escogido un único modelo de tipo exponencial y se han realizado algunas transformaciones en los parámetros a, b y n como variables dependientes de la probabilidad para garantizar altas correlaciones. En efecto, las ecuaciones (3)-(5) sustentan esta dependencia, de manera que fuera del rango de probabilidades establecido por Planos et al. (2011), es decir para prob < 0,50, donde se encuentran la mayoría de los periodos de retorno de Ballester et al. (1996), es posible establecer una tendencia suficientemente razonable para construir los hietogramas correspondientes con dichos periodos de retorno (o probabilidades de ocurrencia), tomando en cuenta la regionalización e intensificación de los STC (ver figura 2).
La evaluación de las ecuaciones (3)-(4)-(5) ha permitido estimar los valores de los parámetros a, b y n del modelo de Wenzel (tabla 6) para las probabilidades que se corresponden con las reportadas por Ballester et al. (1996) y Roura et al. (2018).
Tabla 6 Parámetros regionales de las curvas IDF para STC
| Autor | Región | Sistema | ||||
|---|---|---|---|---|---|---|
| Ballester et al. (1996) | Occidente | CT (STC) | 0,76923 | 1,01096 | 0,05180 | 0,72545 |
| TT | 0,41667 | 0,86667 | 0,03167 | 0,86042 | ||
| H | 0,38461 | 0,85754 | 0,03017 | 0,86965 | ||
| Centro | CT (STC) | 0,33334 | 0,84389 | 0,02786 | 0,88363 | |
| TT | 0,17857 | 0,80881 | 0,02158 | 0,92065 | ||
| H | 0,15873 | 0,80489 | 0,02084 | 0,92490 | ||
| Oriente | CT (STC) | 0,43478 | 0,87206 | 0,03254 | 0,85502 | |
| TT | 0,22223 | 0,81788 | 0,02325 | 0,91093 | ||
| H | 0,20834 | 0,81493 | 0,02271 | 0,91408 | ||
| Roura et al. (2018) | Cuba | CT (STC) | 0,41494 | 0,86617 | 0,03159 | 0,86093 |
La tendencia de las curvas adimensionales IDF de los STCs, para cada región del archipiélago cubano, probabilidad de ocurrencia e intensificación de los sistemas se expone en la figura 3. Nótese que se han superpuesto las obtenidas a partir de Planos et al. (2011) y las de Ballester et al. (1996) para la clasificación de CT (STC). Este análisis ha permitido comprobar que las intensidades adimensionales obtenidas para los periodos de retorno de Ballester et al. (1996) y Roura et al. (2018) son superiores a las derivadas de los estudios de Planos et al. (2011). Algunos de los elementos que pueden incidir en estos resultados son los siguientes:
el periodo que comprendió el estudio: Ballester et al. (1996) de 1791-1996, Planos et al. (2011) de 1961-1990 y Roura et al. (2018), de 1791-2016.
Ballester et al. (1996) y Roura et al. (2018) han dirigido su investigación a la caracterización climatológica de CTs en sus correspondientes periodos, en cambio la investigación de Planos et al. (2011) se enfoca en la caracterización de las precipitaciones en magnitud e intensidad en el archipiélago cubano. En este sentido influye la regionalización e intensificación de los STC establecida por Ballester et al. (1996), elemento que Planos et al. (2011) y Roura et al. (2018) no consideran.
Las curvas (ver tablas 3 y 4) son válidas en todo el archipiélago cubano, pero no permiten identificar aquellas probabilidades con las que afectan los sistemas tropicales ciclónicos a las regiones Occidental, Central y Oriental del país. Por otra parte, los periodos de retorno de estos sistemas, condicionan la estimación de los parámetros a, b y n en las curvas IDF en el modelo empleado, en este caso de Wenzel. Una situación similar acontece con la curva que se identifica con el periodo de retorno obtenido por Roura et al. (2018) en su estudio, (tabla 6), en el que, a pesar de utilizar una base de datos mucho más amplia, carece de una regionalización, pero además, no considera la intensificación de los STC.
BREVE DESCRIPCIÓN DEL MÉTODO DE LA INTENSIDAD INSTANTÁNEA
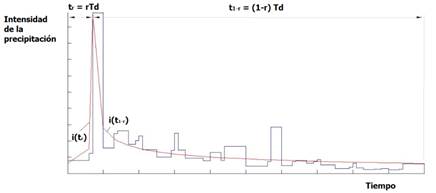
A partir de la utilización de expresiones como las mostradas en la tabla 1, es posible obtener la variación instantánea de la intensidad. En este sentido Chow et al. (1994) desarrolla el método de la intensidad instantánea, cuya principal ventaja es que considera una variación continua de la intensidad de la precipitación a lo largo de su duración T d (ver figura 4).
En efecto, identificado el valor de tiempo
Las relaciones
Como la intensidad media de precipitación
entonces,
Obtención de hietogramas adimensionales para sistemas tropicales ciclónicos
Para la determinación los hietogramas en las regiones especificadas en la presente contribución se aplica el método de la intensidad instantánea (Chow et al. 1994). Para ello se ha definido previamente la intensidad de precipitación instantánea adimensional del k-ésimo instante de tiempo i k , de la manera siguiente:
siendo t = tiempo, I = intensidad instantánea de la precipitación, I
m
= intensidad media definida como P
acum
/T
d
expresada por la ecuación (2),
T
d
= tiempo de duración total de la precipitación asociada al evento ciclónico, P
acum
= precipitación acumulada en la duración T
d
. y finalmente P = precipitación instantánea. Además, se establecen las siguientes relaciones adimensionales de tiempo y precipitación respectivamente:
En la expresión anteriormente obtenida el tiempo es adimensional, siendo además relativo a la relación de avance de la tormenta r, por lo que es definida una escala temporal
En sentido general, los parámetros a identificar en la ecuación (11) son a, b, n y r. Para las regiones Occidental, Central y Oriental los parámetros a, b y n han sido determinados en esta contribución al establecer las curvas IDF para STC. Tales parámetros recogen todas las influencias de las características físico-geográficas de una región, y han de influir significativamente en la intensidad de las precipitaciones.
Sin embargo, el parámetro r que caracteriza la relación de avance de la tormenta, tal y como señala Chow et al. (1994) se determina usualmente calculando la relación entre el tiempo de intensidad máxima y la duración total de la tormenta para una serie de tormentas de diferentes duraciones. La media de estas relaciones, ponderada de acuerdo con la duración de cada evento, es el valor de r.
Existen diferentes valores de este parámetro reportados en la literatura, los cuales tienden a ser menores que 0,5. Wenzel (1982) citado por Chow et al. (1994) reporta valores de r para varios lugares de Estados Unidos y de la India. Cruz (2001) reporta para La Habana, Cuba un valor de r = 0,327 tras analizar 1543 tormentas que afectaron a los actuales territorios de Mayabeque, Artemisa y La Habana.
Planos et al. (2011) consideran que el parámetro r puede ser empleado como complemento del análisis de masa. Según registros de 10 tormentas de origen ciclónico que afectaron al territorio nacional, dichos autores determinaron que r =0,77 evidenciando que la intensidad máxima de los STC ocurre en el cuartil horario final de las mismas. Es válido destacar que este valor es más del doble del reportado por Cruz (2001), el cual en su análisis no clasifica las tormentas empleadas en su estudio a partir de sus génesis, lo cual repercute sin lugar a dudas en sus resultados, además de que Planos et al. (2011) emplearon una amplia red de estaciones distribuidas espacial y altitudinalmente, con una densidad adecuada según normas de diseño fijadas por OMM (2006).
En un trabajo más reciente, Perdigón et al. (2019), analizan 8 CTs que afectaron a todo el territorio nacional y establecen patrones de distribución temporal de precipitaciones a partir de salidas del modelo WRF en las coordenadas de las 3496 estaciones pluviométricas de las redes del Instituto Nacional de Recursos Hidráulicos (INRH) e Instituto de Meteorología (INSMET), según los cuales es posible estimar el parámetro r, resultando la siguiente distribución por regiones del archipiélago cubano: a) Occidente, r = 0,10; b) Centro r = 0,30; c) Oriente r = 0,60. Como ya se mencionó con anterioridad pueden producirse subestimaciones importantes en las precipitaciones, originadas por las propias parametrizaciones establecidas en el WRF,
Ante la dispersión de resultados reportados en la literatura consultada, en esta contribución, se propone un método aproximado para la determinación del coeficiente r a partir del método de intensidad instantánea el cual se desarrolla en detalle seguidamente.
DETERMINACIÓN APROX. DEL COEFICIENTE DE AVANCE DE LA TORMENTA
A partir de la ecuación (11), sujeta a las condiciones (12), es determinada la intensidad adimensional máxima, evaluando para τ = r (equivalente a ζ = 0), o sea:
Sin embargo, al ser el hietograma descrito por (11) una función por tramos, es continua en ζ = 0, pero no es derivable ya que
siendo k un coeficiente muy próximo a 1. En este sentido, mientras k → 1, entonces ε → 0 por lo que la ecuación (11), puede rescribirse como:
A partir de un formal tratamiento algebraico de la ecuación (15), el problema se reduce a encontrar las raíces del siguiente polinomio:
En la ecuación (16), se introduce la sustitución z =
Tomando la raíz positiva, entonces al realizar el cambio de variables correspondiente, es posible arribar a una posible ecuación para r en la forma:
El valor de r tiene carácter regional y a la vez probabilístico, pues depende de los parámetros b y n, asociados con las curvas IDF par CTs. También está determinado por los niveles de aproximación prestablecidos por los coeficientes
En la vecindad previamente considerada, la ecuación (19) puede aproximarse linealmente por:
Igualando las ecuaciones (19) y (20), sustituyendo la ecuación (17) o (18) en la nueva igualdad resultante, es posible arribar a una ecuación más general para el coeficiente de avance de la tormenta r, la cual puede ser escrita formalmente como:
siendo
En la ecuación (21),
A partir de los resultados de la tabla 7, es posible establecer una correlación lineal de tipo
Tabla 7 Coeficientes de avance de la tormenta para CTs
| Autor | Región | Sistema | ||
|---|---|---|---|---|
| Ballester et al. (1996) | Occidente | CT (STC) | ||
| TT | 0,4167 | 0,4584 | ||
| H | 0,3846 | 0,4379 | ||
| Centro | CT (STC) | 0,3334 | 0,4059 | |
| TT | 0,1786 | 0,3169 | ||
| H | 0,1587 | 0,3062 | ||
| Oriente | CT (STC) | 0,4348 | 0,4702 | |
| TT | 0,2222 | 0,3409 | ||
| H | 0,2084 | 0,3331 | ||
| Planos et al. (2011) | Cuba | CT (STC) | 0,9990 | 0,7936 |
| 0,9900 | 0,8690 | |||
| 0,9400 | 0,8106 | |||
| 0,5000 | 0,5134 | |||
| Roura et al. (2018) | Cuba | CT (STC) | 0,4149 | 0,4573 |
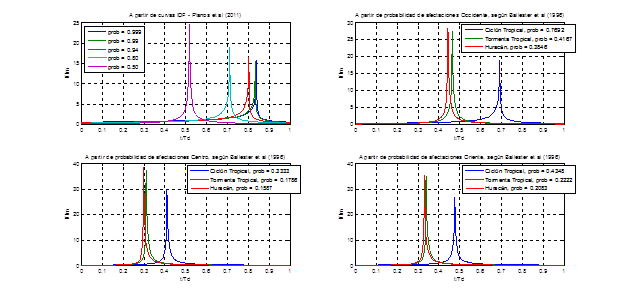
En la figura 5 y tablas 8 y 9 se muestran los hietogramas adimensionales de forma gráfica y tabular respectivamente, para los estudios que han sido analizados en esta contribución. Para escalar los hietogramas, la ecuación (11) se multiplica por
La variable de tiempo
Tabla 8 Hietogramas adimensionales de CTs para diferentes probabilidades de afectación y 24 horas de duración
| t/Td | Probabilidad | |||||||
|---|---|---|---|---|---|---|---|---|
| 0,999 | 0,99 | 0,94 | 0,8 | 0,7692 | 0,5 | 0,4348 | 0,4167 | |
| 0,5413 | 0,4665 | 0,4109 | 0,3331 | 0,2994 | 0,1671 | 0,1462 | 0,1405 | |
| 0,5426 | 0,4677 | 0,412 | 0,3343 | 0,3005 | 0,1682 | 0,1473 | 0,1415 | |
| 0,5451 | 0,4701 | 0,4145 | 0,3367 | 0,3029 | 0,1703 | 0,1494 | 0,1436 | |
| 0,5503 | 0,4751 | 0,4194 | 0,3417 | 0,3078 | 0,1748 | 0,1538 | 0,148 | |
| 0,5557 | 0,4803 | 0,4245 | 0,3469 | 0,3128 | 0,1795 | 0,1585 | 0,1527 | |
| 0,564 | 0,4883 | 0,4324 | 0,3551 | 0,3208 | 0,1872 | 0,1662 | 0,1605 | |
| 0,6336 | 0,556 | 0,5006 | 0,4286 | 0,3933 | 0,2694 | 0,2547 | 0,2509 | |
| 0,6647 | 0,5866 | 0,532 | 0,4645 | 0,4294 | 0,3212 | 0,316 | 0,3157 | |
| 0,6685 | 0,5904 | 0,5359 | 0,469 | 0,434 | 0,3284 | 0,325 | 0,3254 | |
| 0,6698 | 0,5917 | 0,5372 | 0,4706 | 0,4356 | 0,331 | 0,3282 | 0,3288 | |
| 0,6725 | 0,5944 | 0,54 | 0,4739 | 0,4389 | 0,3363 | 0,3349 | 0,336 | |
| 0,6766 | 0,5985 | 0,5443 | 0,4789 | 0,444 | 0,3447 | 0,3456 | 0,3476 | |
| 0,6779 | 0,5997 | 0,5456 | 0,4805 | 0,4456 | 0,3474 | 0,349 | 0,3513 | |
| 0,6904 | 0,6121 | 0,5585 | 0,4959 | 0,4614 | 0,3751 | 0,3851 | 0,3908 | |
| 0,6948 | 0,6165 | 0,5631 | 0,5014 | 0,4671 | 0,3855 | 0,3992 | 0,4063 | |
| 0,6976 | 0,6193 | 0,566 | 0,5049 | 0,4707 | 0,3923 | 0,4085 | 0,4166 | |
| 0,6997 | 0,6214 | 0,5682 | 0,5077 | 0,4735 | 0,3977 | 0,4159 | 0,4248 | |
| 0,7039 | 0,6256 | 0,5726 | 0,513 | 0,479 | 0,4085 | 0,4309 | 0,4417 | |
| 0,7086 | 0,6302 | 0,5775 | 0,5191 | 0,4853 | 0,4213 | 0,4489 | 0,462 | |
| 0,7143 | 0,636 | 0,5835 | 0,5266 | 0,493 | 0,4376 | 0,4726 | 0,4889 | |
| 0,7215 | 0,6431 | 0,5911 | 0,536 | 0,5028 | 0,4593 | 0,5049 | 0,5261 | |
| 0,7371 | 0,6587 | 0,6077 | 0,5571 | 0,5248 | 0,5126 | 0,5892 | 0,6253 | |
| 0,7866 | 0,7087 | 0,6616 | 0,6289 | 0,601 | 0,7665 | 1,1067 | 1,311 | |
| 0,8227 | 0,7454 | 0,7019 | 0,6862 | 0,6632 | 1,1131 | 2,3237 | 3,5462 | |
| 0,8463 | 0,7696 | 0,7288 | 0,7264 | 0,7077 | 1,5166 | 5,6177 | 20,3437 | |
| 0,8477 | 0,771 | 0,7304 | 0,7288 | 0,7104 | 1,5478 | 6,0584 | 27,3646 | |
| 0,8628 | 0,7865 | 0,7478 | 0,7558 | 0,7406 | 1,9779 | 26,7564 | 6,7229 | |
| 0,8955 | 0,8203 | 0,7862 | 0,8178 | 0,8113 | 4,2638 | 3,5183 | 2,3916 | |
| 0,924 | 0,8498 | 0,8203 | 0,8762 | 0,8793 | 24,4774 | 1,9531 | 1,5261 | |
| 0,9909 | 0,9199 | 0,903 | 1,0325 | 1,0689 | 2,0364 | 0,9871 | 0,8566 | |
| 1,4201 | 1,3885 | 1,5403 | 4,4567 | 18,9582 | 0,4401 | 0,3484 | 0,3272 | |
| 1,5367 | 1,5213 | 1,7545 | 18,902 | 2,5353 | 0,3956 | 0,3186 | 0,3002 | |
| 1,8544 | 1,8953 | 2,4751 | 1,5187 | 1,1114 | 0,3327 | 0,2744 | 0,2599 | |
| 2,9303 | 3,3000 | 15,5474 | 0,7854 | 0,6630 | 0,2728 | 0,2300 | 0,219 | |
| 6,8154 | 14,0015 | 1,3703 | 0,6246 | 0,5417 | 0,2462 | 0,2096 | 0,2000 | |
| 14,5827 | 3,4536 | 1,2283 | 0,6034 | 0,525 | 0,242 | 0,2063 | 0,1969 | |
| 0,9407 | 0,8305 | 0,6573 | 0,4553 | 0,4043 | 0,2064 | 0,1782 | 0,1706 | |
| 0,5401 | 0,4653 | 0,4097 | 0,3319 | 0,2982 | 0,1661 | 0,1452 | 0,1394 | |
Tabla 9 Hietogramas adimensionales de CTs para diferentes (continuación de la tabla 8)
| t/Td | Probabilidad | ||||||
|---|---|---|---|---|---|---|---|
| 0,4149 | 0,3846 | 0,3333 | 0,2222 | 0,2083 | 0,1786 | 0,1587 | |
| 0,1399 | 0,1307 | 0,1162 | 0,0887 | 0,0856 | 0,0792 | 0,0751 | |
| 0,141 | 0,1317 | 0,1172 | 0,0897 | 0,0866 | 0,0801 | 0,076 | |
| 0,1431 | 0,1338 | 0,1193 | 0,0917 | 0,0886 | 0,0822 | 0,0781 | |
| 0,1475 | 0,1382 | 0,1236 | 0,0961 | 0,093 | 0,0866 | 0,0825 | |
| 0,1522 | 0,1429 | 0,1284 | 0,1009 | 0,0978 | 0,0915 | 0,0874 | |
| 0,1599 | 0,1507 | 0,1362 | 0,1091 | 0,1061 | 0,0999 | 0,096 | |
| 0,2506 | 0,2454 | 0,2399 | 0,2526 | 0,2586 | 0,2781 | 0,2987 | |
| 0,3158 | 0,3177 | 0,3301 | 0,4601 | 0,5043 | 0,6674 | 0,8932 | |
| 0,3255 | 0,3288 | 0,3449 | 0,5057 | 0,5622 | 0,7812 | 1,1117 | |
| 0,3289 | 0,3328 | 0,3502 | 0,5232 | 0,5848 | 0,8281 | 1,2082 | |
| 0,3362 | 0,3412 | 0,3616 | 0,5626 | 0,6365 | 0,9416 | 1,4594 | |
| 0,3478 | 0,3547 | 0,3804 | 0,634 | 0,7329 | 1,1763 | 2,0645 | |
| 0,3515 | 0,3591 | 0,3865 | 0,6593 | 0,7679 | 1,2699 | 2,3422 | |
| 0,3914 | 0,4065 | 0,4559 | 1,0362 | 1,3442 | 3,7483 | 38,4298 | |
| 0,4071 | 0,4255 | 0,4852 | 1,2661 | 1,7486 | 7,4924 | 15,8194 | |
| 0,4175 | 0,4383 | 0,5055 | 1,4605 | 2,1245 | 14,8774 | 11,0542 | |
| 0,4258 | 0,4486 | 0,522 | 1,6478 | 2,5182 | 37,4798 | 8,8201 | |
| 0,4429 | 0,4699 | 0,5572 | 2,1582 | 3,7653 | 16,2464 | 6,1598 | |
| 0,4635 | 0,496 | 0,6019 | 3,1535 | 7,1312 | 9,2742 | 4,4836 | |
| 0,4907 | 0,5311 | 0,6651 | 6,0446 | 35,3663 | 5,7744 | 3,2979 | |
| 0,5284 | 0,581 | 0,7614 | 35,127 | 11,1977 | 3,7726 | 2,4358 | |
| 0,6293 | 0,7216 | 1,0798 | 5,6291 | 3,7438 | 2,0359 | 1,5091 | |
| 1,3357 | 2,0696 | 29,9604 | 1,183 | 1,0225 | 0,7782 | 0,6628 | |
| 3,7344 | 28,3673 | 2,7547 | 0,7382 | 0,6647 | 0,5407 | 0,4763 | |
| 27,2066 | 4,4553 | 1,64 | 0,5974 | 0,5455 | 0,4547 | 0,4058 | |
| 20,978 | 4,2278 | 1,6019 | 0,5909 | 0,54 | 0,4507 | 0,4024 | |
| 6,2535 | 2,6885 | 1,279 | 0,5297 | 0,4871 | 0,4112 | 0,3695 | |
| 2,3188 | 1,4921 | 0,8988 | 0,4369 | 0,4058 | 0,3488 | 0,3165 | |
| 1,4943 | 1,0859 | 0,7229 | 0,3828 | 0,3577 | 0,3108 | 0,2838 | |
| 0,8457 | 0,6883 | 0,5126 | 0,3045 | 0,287 | 0,2535 | 0,2336 | |
| 0,3252 | 0,2935 | 0,248 | 0,1738 | 0,1662 | 0,151 | 0,1415 | |
| 0,2985 | 0,2708 | 0,2305 | 0,1634 | 0,1565 | 0,1424 | 0,1337 | |
| 0,2586 | 0,2364 | 0,2035 | 0,1468 | 0,1408 | 0,1287 | 0,1210 | |
| 0,218 | 0,2009 | 0,1748 | 0,1285 | 0,1235 | 0,1132 | 0,1067 | |
| 0,1991 | 0,1841 | 0,161 | 0,1194 | 0,1148 | 0,1055 | 0,0996 | |
| 0,1961 | 0,1814 | 0,1588 | 0,1179 | 0,1134 | 0,1042 | 0,0984 | |
| 0,1699 | 0,1578 | 0,1391 | 0,1045 | 0,1007 | 0,0928 | 0,0877 | |
| 0,1389 | 0,1297 | 0,1152 | 0,0877 | 0,0846 | 0,0782 | 0,0741 | |
CONCLUSIONES
En la presente contribución fue aplicado son éxito el modelo de Wenzel en forma adimensional para las curvas IDF de sistemas tropicales ciclónicos a partir de los estudios de Planos et al. (2011), el cual fue extendido con los trabajos de Ballester et al. (1996) y Roura et al. (2018). Fue desarrollado un procedimiento analítico para la determinación aproximada del coeficiente de avance de la tormenta, el cual define el instante de tiempo donde tiene lugar la intensidad máxima de precipitación, lo cual es de vital importancia para estudios hidrológicos e hidráulicos en el diseño de obras de ingeniería. Las probabilidades de ocurrencia de los sistemas estudiados por Ballester et al. (1996), arroja hietogramas de tipo adelantado (r < 0.5) para tormentas tropicales y huracanes, pero cuando estos se agrupan como ciclones tropicales se obtienen de tipo centrado (r ~ 0.5) o retardado (r > 0.5). La clasificación reportada por Planos et al. (2011), en sentido general arroja patrones de distribución temporal de tipo retardado. El procedimiento aplicado no encuentra precedentes en la literatura consultada y fue de vital importancia para la obtención de los hietogramas adimensionales de precipitación para sistemas tropicales ciclónicos, los cuales presentan diversas distribuciones según la intensificación de los mismos, su probabilidad de ocurrencia y la región del archipiélago cubano afectada, llenándose así un vacío existente en el tratamiento de valores extremos hidrometeorológicos.