Custom services
Spanish (pdf)
Article in xml format
Article references
Send this article by e-mail
Cited by SciELO 
Similars in
SciELO 
Permalink
INTRODUCCIÓN
Indiscutiblemente el uso de los asistentes matemáticos se ha incrementado en los últimos años del presente siglo, pero otra cosa es el buen uso de estos, lo cual no quiere decir que siempre se usen sin un buen aprovechamiento de los recursos que brindan para mejorar el aprendizaje de los contenidos matemáticos que se presenta a los estudiantes.
Uno de los problemas generales que se presenta en el trabajo con los asistentes matemáticos en las aulas es su uso anárquico pues aún en instituciones que plantean indicaciones específicas para su uso, cada docente generalmente las interpreta a su manera y los usan de acuerdo con su interpretación, en unos casos porque no tienen la preparación suficiente para seguir las indicaciones dadas, en otras por facilismo y también por considerar que sus criterios al respecto son los adecuados (Morales & Blanco, 2019). Por otra parte, es cierto que una teoría o metodología para el uso de los asistentes matemáticos está lejos de existir, fundamentalmente porque cada contenido y cada nivel escolar tiene sus particularidades y se puede decir que hasta cada grupo de alumnos.
Por lo tanto, entendemos que una vía para llegar a un consenso es continuar trabajando en propuestas con cierto grado de generalidad y fundamentos didácticos, para lograr que los docentes en los diferentes niveles escolares ganen experiencia en el uso de los asistentes matemáticos a través de experiencias compartidas que les permitan ganar eficiencia en el uso de los mismos.
Uno de los usos que menos aporta es cuando se utilizan como simples calculadoras, en lo que no incluimos su uso cuando se resuelven problemas de optimización y a través de los asistentes matemáticos se resuelven las ecuaciones que permiten hallar los puntos extremos, pues en este contenido, la esencia del mismo es que los estudiantes puedan arribar a dichas ecuaciones. Es decir, plantear el modelo matemático que permite la solución del problema, en cuyos modelos pueden aparecer ecuaciones con cierto grado de dificultad, en estos casos es aconsejable resolver dichas ecuaciones mediante el uso de los asistentes matemáticos, logrando así que los estudiantes se enfoquen en la construcción del modelo matemático del problema.
Otro punto débil en el trabajo con dichos asistentes es cuando se propicia que los estudiantes concluyan que no necesitan saber gran cosa de matemática porque la computadora lo hace todo, lo cual no sucedería si en la enseñanza de la disciplina se trabajara fundamentalmente con la resolución de problema y no con ejercicios y tareas de cálculo. Es conocido que la resolución de problemas es un tema complejo en el proceso enseñanza-aprendizaje de la Matemática. Dado que la generalidad de los estudiantes considera que la Matemática es difícil (Heredia & Fernández, 2017), ven los asistentes matemáticos más como un medio para librarse de las dificultades de la Matemática, que, como un medio para comprenderla mejor, reduciendo el nivel de dificultad.
Este artículo tiene como objetivo identificar los errores más frecuentes que cometen los estudiantes en la interpretación de los gráficos que devuelven los asistentes matemáticos, así como brindar algunas orientaciones para evitarlos.
MÉTODOS
A partir del estudio bibliográfico realizado se consideró oportuno analizar el comportamiento de los estudiantes de la Universidad Autónoma de Santo Domingo en el uso de los asistentes matemáticos, en específico en la interpretación de los resultados que se obtienen con el uso de estos, para lo cual se siguió una metodología cualitativa-cuantitativa.
Se elaboró un cuestionario a tales efectos con ocho preguntas con características no cotidianas, es decir, situaciones que los alumnos no enfrentan con frecuencia, pero sobre contenidos elementales del cálculo diferencial. Se orientó a los estudiantes trabajar con el asistente GeoGebra, ya que todos los estudiantes encuestados afirmaron estar familiarizado con el uso del mismo.
Participaron un total de 30 estudiantes de segundo año de las carreras de Ingeniería Civil y Eléctrica, los cuales se ofrecieron voluntariamente a participar en el estudio. No se aceptaron estudiantes de Ingeniería en Informática, pues se asumió que no eran representativos del resto de las carreras de ingeniería, ya que su especialidad está muy ligada al uso de los medios de cómputo.
RESULTADOS Y DISCUSIÓN
Los asistentes matemáticos en el proceso enseñanza-aprendizaje de la Matemática
Se debe tener en cuenta que el uso de los asistentes matemáticos se encuentran en consonancia con el respaldo que ha tenido en la comunidad científica que trabaja en el proceso enseñanza-aprendizaje de la Matemática los trabajos de R. Duval sobre la transferencia de registros de representación semiótica (Duval, R, 2006a, 2006b, 2006c) lo que indica la necesidad y efectividad de los cambios de representación en lo cual juegan un papel fundamental los asistentes matemáticos, dada la facilidad y agilidad con la que permiten efectuar cambios de representación, donde también es necesaria una correcta interpretación de las representaciones que aparecen en pantalla, en particular de las representaciones gráficas.
Tal como plantean De Olivera & Cheng (2011) las imagines visuales, entendidas como representaciones materializadas en símbolos analíticos, literales o gráficos de los objetos matemáticos, propician una comprensión de los objetos matemáticos que el lenguaje natural y el simbolismo matemático no pueden ofrecer, pero evidentemente el que observa la imagen debe poder interpretar matemáticamente dichas imágenes. A lo que se debe agregar que el potencial semiótico de estos instrumentos de mediación radica en la doble interrelación que ocurre entre el instrumento y el significado personal resultante de su uso para el logro de una tarea en correspondencia con el conocimiento institucionalmente establecido (Mariotti, 2013).
Otro problema, desde el punto de vista didáctico, que se manifiesta en el trabajo con los asistentes matemáticos es su uso para resolver problemas relativamente simples, sin poner atención por demás, en los aspectos conceptuales involucrados en el problema, esto indudablemente induce a los estudiantes a subestimar la necesidad del conocimiento conceptual y propicia que tengan dificultades para interpretar situaciones no convencionales, además de desperdiciar las potencialidades de estos asistentes para resolver problemas interesantes y consolidar el uso de los concepto matemáticos (Ochkov & Bogomolova, 2015).
El uso mecánico de los asistentes matemáticos puede conducir a los estudiantes a no comprender situaciones relativamente simples, como es el caso de no percatarse porque la computadora cuando tratan de escalonar la siguiente matriz le devuelve una matriz no escalonada (Fig. 1):
Lo cual viene como consecuencia de la sencilla razón de no haber comprobado que el determinante de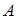 
es distinto de cero: 
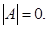Lo anterior es algo relativamente sencillo, ya que mediante el conocimiento conceptual de las propiedades de los determinantes, se puede visualizar que la tercera columna es una combinación lineal de la primera y la segunda (la tercera columna es el resultado de sumar la primera y la segunda).
En un trabajo realizado por Morales & Blanco (2019) en el que se hace una amplia revisión bibliográfica sobre el uso de los asistentes matemáticos, se pudo apreciar que se reportan abundantes ventajas de su uso en el proceso enseñanza-aprendizaje de la Matemática, como son: reforzar el razonamiento de los estudiantes, la interpretación gráfica de los conceptos matemáticos, resolver ecuaciones complicadas durante la resolución de un problema, entre otra muchas ventajas. Aunque también se destacaron desventajas de su uso, como son que el estudiante se conforme con la solución que le brinda el software sin preocuparse por comprender el proceso de resolución del problema, y que el estudiante se concentre más en el uso del software que en la compresión de los conceptos en juego. Se destaca que ventajas importantes que pueden resultar del uso de los asistentes matemáticos, tales como la visualización de principios matemáticos, descubrir relaciones y patrones, realizar y comprobar conjeturas, resultan sesgadas por las limitaciones de los estudiantes para interpretar correctamente lo que ven en pantalla (Morales & Blanco, 2019); también se han encontrado insuficiencias de los docentes en el dominio de los contenidos didáctico-tecnológicos para la utilización adecuada de las TIC en función de las necesidades de aprendizaje de los estudiantes y de las situaciones de aprendizaje (Fortuna, Montes & Guerrero, 2018).
Por lo que el presente trabajo se ha enfocado en mostrar vías para lograr que los estudiantes puedan apreciar que para usar los asistentes matemáticos también deben saber Matemática. Para lo cual se ilustran situaciones en las que se requiere el conocimiento matemático para interpretar lo que devuelven los asistentes matemáticos en la resolución de una tarea determinada.
En ocasiones, las imprecisiones en el conocimiento matemático conduce a los estudiantes a no sacar conclusiones correctas del gráfico que devuelve el asistente matemático, como es el caso en que los estudiantes no identifican el eje x como asíntota de la función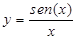 
, porque traen el concepto ingenuo de la enseñanza precedente de que la asíntota es la recta que se acerca indefinidamente a la curva y no que la distancia entre la curva y la asíntota tiende a cero (Báez, 2018).
En un estudio realizado, se pudo apreciar que muchos estudiantes tenían dificultades para interpretar relaciones no funcionales, (no uno a uno), que tendían a interpretar funciones dadas en diferentes representaciones como entidades diferentes y consideraban las funciones exponenciales con dominio acotado por su falta de habilidad para explorar el comportamiento del gráfico (Jung-Chih & Yung-Ling. 2015).
Errores generales en la interpretación de los gráficos
Con cierta generalidad, en la interpretación de los gráficos se cometen errores, los que se referencian en la literatura especializada (Copelad, 2018) y han sido verificado como tales en Báez (2018) y Heredia (2018). Se trata de errores que no solo se cometen en la interpretación del gráfico que devuelve un software, sino de aspectos a tener en cuenta a la hora de orientar a los estudiantes. Dichos errores se pueden clasificar en:
Diferenciación entre gráficas continuas y gráficas discretas.
Escritura relativa e interpretación.
Concepto de variable y notación.
Como consecuencia de la interpretación de una gráfica continua como discreta los estudiantes presentan las siguientes fallas:
Falta de claridad sobre el significado de la línea no interrumpida.
Tendencia a mirar sólo los puntos marcados sobre la gráfica negando la existencia de puntos entre ellos.
Asignación de un número de puntos no definidos (real o entero) al espacio gráfico existente entre dos puntos que representan datos continuos.
De manera similar, los estudiantes enuncian el número de unidades del eje X que están entre un punto a y un punto b.
Como consecuencia de la interpretación de una gráfica discreta como continua los estudiantes presentan las siguientes fallas:
Escritura relativa e interpretación
Los estudiantes presentan dificultades para analizar las relaciones entre los datos, lo cual les dificulta interpretarlos correctamente. Estas dificultades pueden ser clasificadas en dos categorías: 1) Confusión intervalo / punto, y 2) interpretaciones icónicas.
La confusión intervalo / punto se debe a que los estudiantes cuando enfrentan el análisis de las gráficas enfocan su atención a un punto o a un grupo de puntos en lugar de hacerlo sobre un rango de ellos que es lo que les permite identificar relaciones y características globales de las gráficas como su forma general, intervalos, pendientes, etc. Este es el caso cuando los estudiantes prueban que: x1 > x2 y f(x1) > f(x2) y afirman que la función es creciente en un intervalo [a, b] si garantizar que lo planteado se cumple para toda x en el referido intervalo.
La Interpretación icónica se presenta cuando los estudiantes interpretan una gráfica como un objeto, o sea una representación pictórica de la situación, por lo que no son capaces de inferir el comportamiento de la función más allá de lo que aparece en la gráfica. Sucede cuando el estudiante representa una ecuación polinómica de grado cuatro y aparecen en pantalla solo tres intersecciones con el eje x, por lo que plantean que la ecuación tiene tres raíces reales, sin tener en cuenta que las raíces complejas en las ecuaciones polinómicas se presentan por pares, por lo que no es posible que una ecuación polinómica de grado cuatro tenga solo tres raíces reales.
Concepto de variable y notación
Los estudiantes consideran que al cambiar el símbolo que designa una variable en una ecuación funcional cambian algunos aspectos críticos de la función. Por ejemplo, en los gráficos para estudiar la relación espacio-tiempo que se usan “e” y “t” para los ejes coordenados. Los estudiantes creen que las escalas sobre los ejes X e Y necesitan ser simétricas, aun cuando ello no les permita hacer la gráfica más accesible visualmente. Además, en muchos casos los estudiantes no poseen los recursos para cambiar las relaciones entre las escalas de los ejes. Lograr que los estudiantes eliminen estos errores es un paso importante para que puedan interpretar eficientemente los gráficos que le devuelven los asistentes matemáticos.
Otro aspecto importante en el uso de los asistentes matemáticos es la posibilidad que estos brindan para analizar las interrelaciones entre los elementos representados y entre estos y el objeto de estudio según el contexto en el que se trabaja. En general, en las prácticas sobre graficar funciones no se incluyen tareas donde los estudiantes tengan que trabajar con las interrelaciones entre las variables existentes en la gráfica, entre ellas y los fenómenos representados, y entre los fenómenos y el concepto de función. Es un hecho que cuando se asignan tareas a los estudiantes para contribuir a la consolidación de un concepto, si en dichas tareas no está presente una característica esencial del concepto, los estudiantes ignorarán dicha característica esencial (Byas & Blanco, 2017).
Este error didáctico puede crear muchas concepciones erróneas, ya que si el estudiante trabaja en un contexto restringido en el cual todos los ejemplos considerados tienen una cierta propiedad, en la ausencia de contra ejemplos que muestren lo contrario, el estudiante asume que dichas propiedades se cumplen en otros contextos, este es el caso cuando el estudiante no tiene en cuenta las hipótesis de continuidad porque solo se le han asignados tareas donde la funciones en juego son continuas; también sucede cuando se quiere entrenar a los estudiantes en el cálculo de la inversa de una función y, solo se le asignan tareas donde la función es biyectiva.
Barnard & Tall, (1997) plantean que la habilidad para construir múltiples y flexibles conexiones entre diferentes unidades de conocimientos y entre ellas mismas, es un aspecto fundamental para que los estudiantes puedan obtener informaciones importantes para el trabajo que realizan y además es un aspecto clave en el pensamiento matemático. Por lo que es una necesidad, desde el punto de vista de la enseñanza de la Matemática que los estudiantes puedan establecer conexiones correctas y eficientes entre las expresiones analíticas y los gráficos representados por los asistentes matemáticos, así como el uso de diferentes representaciones, ya que cada representación enfatiza algunos aspectos del objeto, pero ignora otros y los aspectos ignorados no estarán incluidos en el conocimiento del objeto por el estudiante. Como es el caso cuando el hortocentro y el circuncentro siempre se representan dentro del triángulo.
Necesidad del conocimiento matemático en el trabajo con la computadora
La importancia del uso de los asistentes matemáticos no se puede separar del conocimiento matemático. Se ha podido observar que la comprensión de los gráficos generados por la tecnología no es inmediata, incluso algunos docentes tienen dificultades para conciliar su conocimiento con lo que ven en pantalla.
Los estudiantes generalmente saben que si A > 0: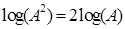 
, y cuando tienen el caso de 
y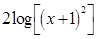 
no tienen problemas con la interpretación de su representación gráfica pues el argumento del logaritmo es positivo, pero en el caso de 
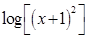y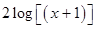 
los gráficos no coinciden, o mejor dicho solo coinciden en la parte donde el argumento del logaritmo es positivo, por lo que el estudiante que olvida que la función logaritmo, en los números reales, solo está definida para valores positivos de su argumento, concluye que el gráfico está mal o que la referida propiedad de los logaritmos no siempre se cumple, lo que lo puede llevar a un error todavía mayor que es pensar que en Matemática, bajo las mismas hipótesis puede haber excepciones.
Otra situación se presenta al graficar 
el gráfico que devuelve la computadora no se asemeja mucho al conocido gráfico del seno; en este caso el estudiante debe tener en cuenta la alteración en el periodo del seno que introduce el factor 50, ya que el periodo es: ; luego para poder ver en pantalla el contorno real del gráfico es necesario ponerle un intervalo adecuado a los ejes, donde se puede ver que la función mantiene el comportamiento gráfico pero con un periodo diferente, (Fig. 2 y 3).
Este error es derivado del hecho de que en general los estudiantes no se entrenan en trabajar con periodos de las funciones trigonométricas con periodos muy grandes o muy pequeños.
De la misma manera al graficar 
el gráfico que resulta no permite apreciar el efecto del segundo sumando en el gráfico de la función, dado el valor pequeño de dicho sumando, (Fig. 4):
Por lo que se requiere graficar la función en el intervalo adecuado, (Fig. 5):
Además el estudiante puede pensar que el gráfico indica puntos angulosos donde no debe existir la derivada, lo cual se contradice con que efectivamente la función tiene derivada en todos sus puntos, por lo que se requiere hacer un zoom en un segmento del gráfico para mostrar la correspondencia del gráfico con el aspecto analítico de la función (figura 6), esto es:
De modo que el estudiante pueda apreciar que el gráfico coincide con las características de la función.
El conocimiento matemático resulta necesario para el trabajo eficiente con los asistentes matemáticos, sin el conocimiento matemático de lo que se grafica la interpretación de lo que aparece en pantalla, no siempre es correcta, por ejemplo, el gráfico de la función: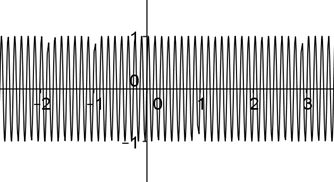 
en el intervalo [-90, 90] produce un gráfico con un aparente punto anguloso en (0, 1), como se ilustra en la figura 7, en la cual se supone que no exista la derivada, lo que contradice el hecho de que la función es derivable en dicho punto.
Por lo que resulta necesario explicar a los estudiantes los recursos para ajustar las dimensiones de los ejes de tal forma que se pueda interpretar correctamente el gráfico que devulve la computadora, según las características del objeto matemático que se representa. Pero además para poder hacer los ajustes necesarios para obtener la representación adecuada son necesarios los conocimientos matemáticos de los objetos con los que se trabaja. Estos ejemplos son importantes no solo para que el estudiante pueda interpretar correctamente lo que aparece en pantalla, también para que pueda apreciar que los asistentes matemáticos, aunque son herramientas poderosas y de gran ayuda, no los eximen de la necesidad de poseer los conocimientos matemáticos necesarios.
Otro error didáctico que se manifiesta en el uso de los asistentes matemáticos, está dado por la propia eficiencia que estos poseen en la actualidad, por lo que muchos estudiantes e incluso algunos docentes suelen identificar las raíces de una ecuación por las intercepciones del gráfico de la misma con el eje x, lo cual funciona bien en casos sencillos con raíces que se corresponden con la escala de los ejes coordenados, aun en el caso de raíces racionales, aunque en la escala de los ejes aparece en notación decimal; pero es importante que los profesores expliquen a sus estudiantes que el gráfico solo representa una aproximación del valor de la raíz que no siempre coincide con la raíz exacta, como es el caso del siguiente ejemplo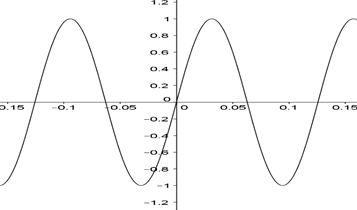 
= 0 donde aparentemente las raíces de son 
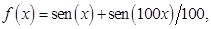pero el valor verdadero de la tercera raíz es 
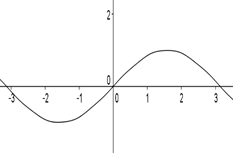lo que no se refleja en la figura 8.
Otro aspecto que generalmente no se tiene en cuenta es el trabajo con problemas donde se requiera el uso de valores numéricos relativamente grandes para poder apreciar el resultado visualmente, como es el caso en el siguiente límite:
para cualquier n fijo.La tendencia de este límite al infinito está asociada al parámetro a, por lo que de forma racional el estudiante puede pensar que para valores extremadamente pequeños del parámetro, el limite puede no tender a infinito, por lo que es necesario recurrir a ejemplos con valores del parámetro pequeños, para que el estudiante pueda apreciar que efectivamente el límite tiende a infinito, por ejemplo: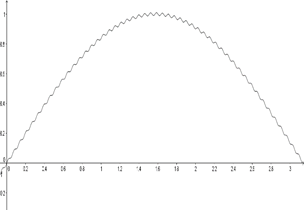 
por lo que es suficiente que a sea algo mayor que cero para que el límite tienda a infinito.
Análisis de los resultados del cuestionario
Las preguntas que componen la encuesta son relativas al tipo de situaciones que fueron analizadas en el presente trabajo, todos los estudiantes que participaron en la encuesta disponían de medios de cómputo en el momento de la realización de esta y supuestamente tenían los conocimientos suficientes para trabajar con los mismos.
La primera pregunta pedía encontrar las raíces de una ecuación polinómica de grado cinco con cinco raíces reales, pero dos muy próximas, por lo que el gráfico, usando la dimensión usual de los ejes solo mostraba 4 raíces. De los 30 alumnos encuestados 26 dieron las 4 raíces, que mostraba el gráfico, como solución de la ecuación, uno dijo que sabía que faltaba una raíz, pero no sabía cómo encontrarla. Esto es, solo 4 estudiantes conocían la relación entre las raíces de una ecuación polinómica y el grado de la ecuación y solo 3 pudieron manipular el gráfico para encontrar la raíz faltante. Esta pregunta muestra que no siempre los estudiantes tienen los conocimientos matemáticos necesarios, para interpretar el resultado que ven en pantalla.
En la segunda pregunta se planteó una ecuación polinómica de grado 3 con raíces -1, 0 y 1.02; dada la ecuación se les pedía hallar las raíces y comprobar el resultado. 25 estudiantes graficaron la ecuación y asumieron las raíces -1, 0 y 1, atribuyendo la falta de concordancia en la comprobación a inexactitudes del software, 2 resolvieron la ecuación analíticamente y 3 manipularon las dimensiones de los ejes para obtener una mejor aproximación. Nótese que en este caso se pide comprobar el valor de las raíces de la ecuación.
En la tercera pregunta se les pidió representar gráficamente 
en el intervalo 
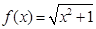siendo
una función con dominio y recorrido en los números naturales. 25 estudiantes representaron un segmento como si fuera una función de R en R, los 5 restantes lo hicieron correctamente. Esto muestra la tendencia de los estudiantes a no considerar el dominio de las funciones con las que trabajan y representar todos los gráficos como si fueran con dominio y recorrido en los reales. Lo cual muestra el error referido anteriormente donde los estudiantes interpretan gráficas discretas como si fueran continuas.
En la cuarta pregunta se les pidió encontrar aproximadamente los extremos relativos de la función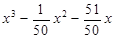 
sin calcular el valor exacto, 23 estudiantes no respondieron la pregunta, 3 plantearon los extremos absolutos, solo 4 respondieron correctamente. Esta pregunta mostró tanto falta de conocimientos matemáticos (no distinguir los extremos absolutos de los relativos) como falta de recursos para trabajar con los asistentes matemáticos.
En la quinta pregunta se les pidió explicar o mostrar el efecto del segundo sumando de la función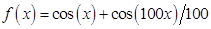 
en el gráfico de la función. En este caso solo 3 estudiantes pudieron satisfacer la pregunta correctamente, 4 plantearon argumentos incorrectos y el resto no respondió. Dado el pequeño valor del segundo sumando, al graficar la función con la escala usual de los ejes, la influencia de dicho sumando no se refleja en el gráfico, por lo que la mayoría de los estudiantes no supo que responder al respecto.
En la sexta pregunta se les pidió representar gráficamente las tangentes a la curva 
en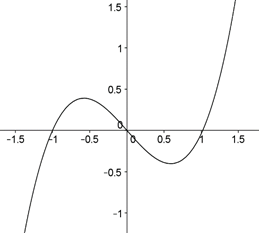 
17 no respondieron, 9 estudiantes plantearon que al parecer la curva no tenía tangentes en dichos puntos y solo 4 estudiantes representaron las tangentes verticales. En la respuesta a esta pregunta interviene notablemente el conocimiento matemático, pues usualmente los estudiantes no asocian la tangente trigonométrica del ángulo de 90 grados, con la tangente geométrica vertical a una curva.
En la séptima pregunta se les pidió que explicaran la causa o causas de la diferencia fundamental entre los gráficos de 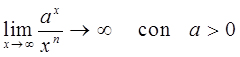y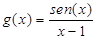 
. En este caso 16 estudiantes no respondieron o plantearon argumentos fuera de lugar, 5 plantearon que tenían diferentes discontinuidades, lo cual era evidente del gráfico, 9 respondieron correctamente que en el primer caso la discontinuidad es evitable y en el segundo no. Aquí también hay que tener en cuenta que muchos estudiantes no tienen claro el concepto de discontinuidad evitable.
En la octava pregunta se les pidió decir los puntos de discontinuidad de la función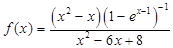 
para lo cual se podían apoyar en el gráfico de la función. En este caso el gráfico en pantalla los indujo a notar solo las discontinuidades que se mostraban en el gráfico, pasando por alto la discontinuidad en 
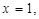por una parte, porque la causa de la discontinuidad aparece en el numerador y por otra porque no se ve explícitamente en el gráfico de la función. Esta pregunta muestra que efectivamente los estudiantes tienden a tomar el resultado que le devuelve el asistente matemático sin hacer un análisis del mismo. De los 30 estudiantes solo 4 respondieron correctamente, los restantes solo señalaron las discontinuidades en 
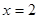y 
El resultado de la encuesta muestra categóricamente que el 90 por ciento de los estudiantes que participaron, solo han usado el GeoGebra para resolver tareas que no requieren de un buen conocimiento matemático para interpretar el resultado que devuelve el asistente matemático y no conocen o no están entrenados en cambiar las dimensiones de los ejes coordenados para facilitar o poder apreciar las características reales del gráfico que aparece en pantalla.
Esto indica la necesidad de entrenar a los estudiantes en el manejo de las dimensiones de los ejes, tanto en sus dimensiones, como en la proporción de sus dimensiones, las cuales muchos estudiantes consideran que deben ser las mismas en ambos ejes, evidentemente hay casos en que efectivamente los ejes deben tener las mismas dimensiones, pero esto no siempre es así, por lo que el estudiante debe tener los conocimientos matemáticos necesarios para decidir cuándo es conveniente usar o no diferentes proporciones en los ejes coordenados.
El análisis cualitativo permite asegurar que solo el 10 por ciento de los estudiantes encuestados son capaces de enfrentar exitosamente la resolución de problemas no convencionales, problemas de casos extremos, como a veces se refieren en la literatura, con el uso de los asistentes matemáticos, porque los tres estudiantes que respondieron correctamente en las ocho preguntas siempre fueron los mismos.
Es usual que los estudiantes que alcanzan cierto dominio de los asistentes matemáticos tiendan a subestimar la necesidad de los conocimientos matemáticos, por lo que es necesario asignarles tareas cuya solución no dependa exclusivamente de un buen uso de estos asistentes, ya que el dominio conceptual y el buen uso de los asistentes deben marchar a la par.
CONCLUSIONES
El estudio realizado permitió corroborar lo planteado en la bibliografía especializada respecto a dificultades que presentan los estudiantes en el uso de los asistentes matemáticos, en particular en la interpretación de los resultados que aparecen en pantalla. Estos resultados indican la necesidad de llegar a consenso en la comunidad científica sobre indicaciones didácticas correctamente fundamentadas, para lograr una buena dirección de la actividad de los estudiantes en el uso de estos medios.
También destaca la importancia de los asistentes matemáticos, asociados a los cambios de representación semiótica, dada la importancia que los especialistas han atribuido a la necesidad de los cambios de representación semiótica para la apropiación conceptual de los estudiantes, ya que mediante el uso de los mismos permite agilizar e incrementar los cambios de representación; eficiencia que depende efectivamente del entrenamiento que tengan los estudiantes para interpretar lo que ven en pantalla, de modo que sean capaces de identificar el mismo objeto en sus diferentes representaciones
